平行轴圆柱线圈互感计算的新方法

罗 垚

（武汉大学动力与机械学院 武汉 430072）



平行轴圆柱线圈互感计算的新方法

罗 垚

（武汉大学动力与机械学院 武汉 430072）

摘要运用倒数距离在圆柱坐标中的一种解耦展开公式，提出了以变形Bessel函数和变形Struve函数表示的平行轴圆柱线圈互感的新表达式。随后进一步对所得表达式进行了渐近展开以利于数值计算。数值计算表明，变形Bessel函数和变形Struve函数的单调性有利于提高平行轴圆柱线圈的互感计算效率，尤其对于径向较厚的扁线圈或圆盘线圈。相对于同样准确度的计算结果，提出的方法较已有的方法快1～2个数量级，而这些已有方法采用的是振荡的Bessel和Struve函数。最后，对于共面圆环提出了一种以Gauss超几何函数表达的闭式解，该解的正确性亦由数值计算确认。

关键词：互感 变形Bessel函数 渐近展开

0 引言

对于近年来兴起的无线能量传输系统，其核心部分大量采用平行轴圆柱线圈[1-3]，而圆柱线圈的互感值是无线能量传输效率的重要因素，故准确而高效的圆柱线圈互感计算方法具有重要的实用价值。文献[4]中已有近似公式对这一问题进行处理，但这些公式较为复杂且准确度不高，求解时往往需要借助专门绘制的曲线和数表。此外，纯数值方法（FEM，BEM等）则难以对电磁场问题进行逆向求解（例如给定互感值求线圈的几何参数），因而对圆柱线圈互感问题的解析或半解析处理是极为必要的。在无线能量传输系统的实际应用中，两互感线圈不可能总保持同轴，对此一般采用文献[5]中给出的平行轴圆柱线圈计算公式。在文献[5]中，圆柱线圈的互感首次以Bessel函数Jn（x）及Struve函数Hn（x）准确解出。此法将两圆柱线圈的相对方位分为三种情况并得出了五个不同的公式来完整描述两个线圈相对方位的所有可能情形。此法比以往任何公式都更为简洁，并尤其适用于求解具有较小径向参数和较大轴向参数的线圈互感。两线圈各几何参数如图1所示。

图1　平行轴矩形截面圆柱线圈侧视图，两线圈匝数分别为N1、N2，线圈径向参数为R1～R4及r0,轴向参数为2h1、2h2和z0Fig.1 Side view of two circular coils of rectangular cross section,with the turns of N1and N2,respectively,the radial parameters of R1～R4and r0,the axial parameters of 2h1,2h2and z0

然而，由于文献[5]中方法的被积函数的径向参数依赖于非周期振荡函数Jn（kr）及Hn（kr），而其轴向参数依赖于指数衰减函数e-kh及e-kz0，故此法并不适用于求解具有较大径向参数和较小轴向参数的线圈互感，但在实际应用中，具有这种几何特性的线圈（例如圆盘线圈）是被广泛应用的。同时，若考虑在实轴上单调的变形Bessel函数In（x）、Kn（x）以及变形Struve函数Ln（x），则此种单调性可能有助于互感数值积分的计算。推导以下这种以变形Bessel函数和变形Struve函数表示出的互感表达式并将其计算性能与已有方法进行比较。本文所用到的特殊函数见表1。

表1　本文用到的特殊函数Tab.1 Special functions applied

1 含变形Bessel函数的互感积分公式

限于篇幅，本文在以下推导中仅列出主要步骤。首先考虑两平行轴圆环，其半径分别为r1、r2，分别位于相距z0的平行平面上，且它们的轴间距离为r0。它们之间的互感为[5]

式中，μ0＝4π×10-7H/m为真空磁导率。为了将式（1）写为含变形Bessel函数In（x）和Kn（x）的表达式，现运用倒数距离展开[6]

式中

且

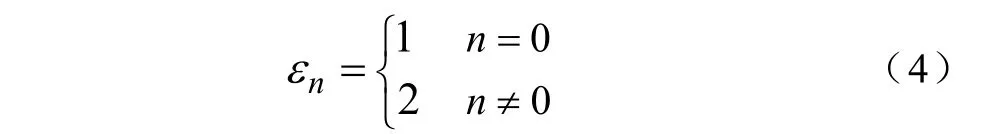
式中，εn为Neumann因子。在经过一些计算之后可将式（1）的互感表达式变为

或

式（5）、式（6）是以下推导各类圆柱线圈互感公式的基础。

现有两平行轴单层圆柱线圈（螺线管），其半径为r1、r2，其他线圈参数可参考图1。为了计算这两个线圈间的互感，令式（1）、式（5）和式（6）中的轴向参数，并对z1、z2积分，在简单的计算之后可得表达式

（1）对r0≥r1＋r2

（2）对0≤r0≤r2-r1

（3）对z0≥h1＋h2

式（7）～式（9）与文献[7]中给出的结果一致。两平行轴螺线管的互感即可由式（7）～式（9）的数值积分求得。

设有两平行轴圆盘线圈，它们可视为h1＝h2＝0的圆柱线圈，其他线圈参数如图1所示。为了计算这两个线圈间的互感，对式（1）、式（5）和式（6）的径向参数r1、r2积分并运用式（10）～式（12）进行积分。

于是可得

（1）对r0≥R2＋R4

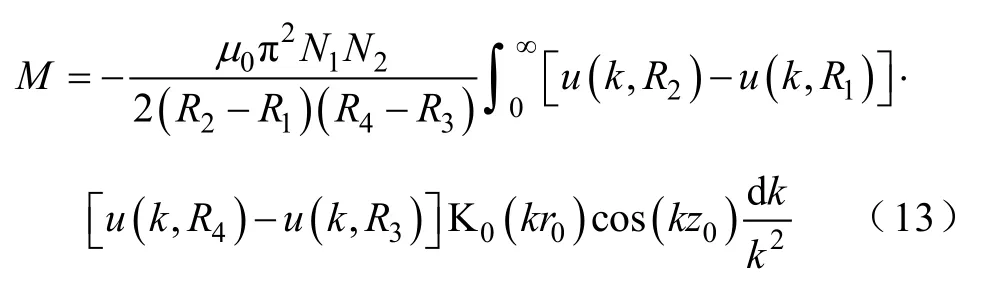
（2）对0≤r0≤R3-R2

（3）对径向参数无任何限制的圆盘线圈

式（12）、式（13）即为含有变形Bessel函数与变形Struve函数的互感表达式。式（15）与文献[5]中给出的结果一致。两平行轴圆盘线圈的互感即可由式（13）～式（15）的数值积分求得。

设有两矩形截面圆柱线圈，其线圈参数如图1所示。为了计算这两个线圈间的互感，令式（1）、式（5）和式（6）中的轴向参数，并对z1、z2积分，再对径向参数r1、r2积分，并由式（10）～式（12），可得

（1）对r0≥R2＋R4

（2）对0≤r0≤R3-R2

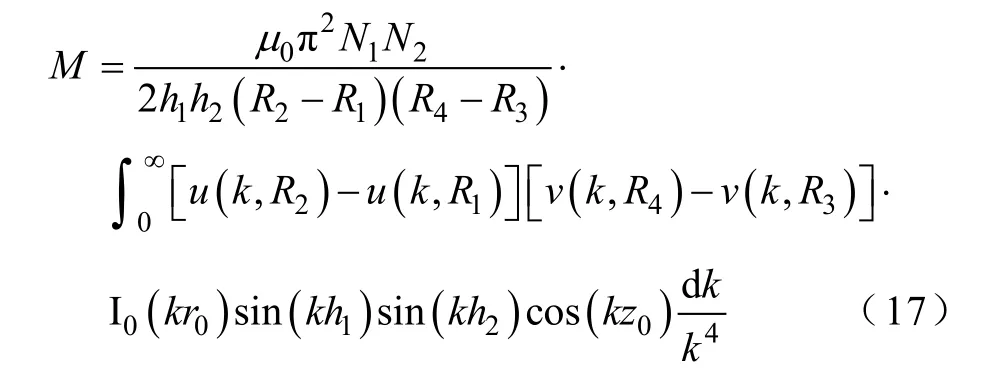
（3）对z0≥h1＋h2

两平行轴矩形截面圆柱线圈的互感即可由式（16）～式（18）的数值积分求得。进一步注意变形Bessel函数I0,1（x）、K0,1（x）及变形Struve函数L0,1（x）的非振荡特性。实际上，若n≥0，在整个正实轴0 ＜x＜∞上，In（x）及Ln（x）均单调增加而Kn（x）呈指数型单调递减。因而对比文献[5]中的表达式，此处将J0,1（x）、H0,1（x）复杂的振荡性质转移到振荡性质非常简单的三角函数上，这种转移将有利于数值积分的实行。对两共面圆环z0＝0，式（5）或式（6）可被进一步求积为闭式

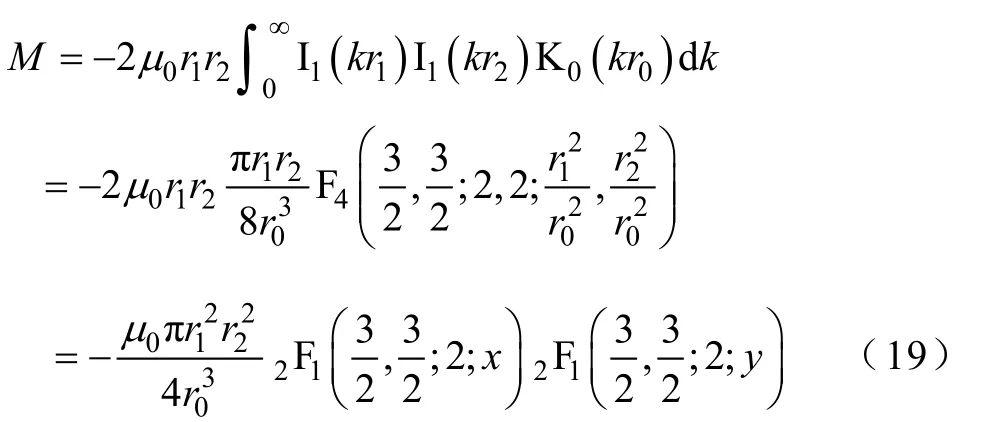
式中

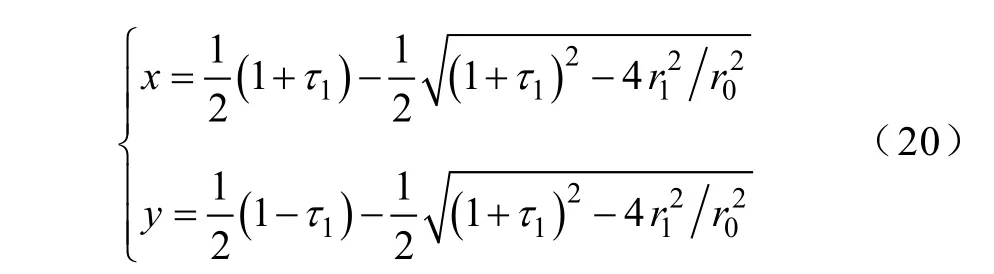
且

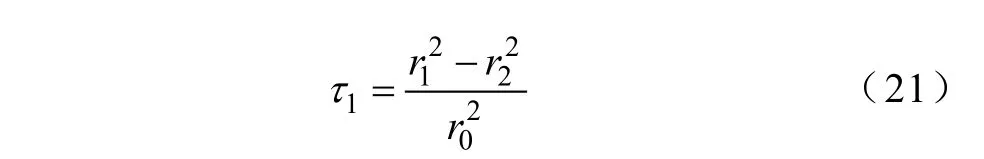
或有

式中

且

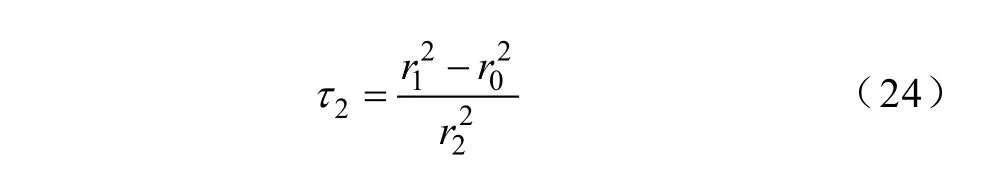
式（19）～式（21）与文献[8]中给出的结果一致，适用于r0＞r1＋r2的情形。式（22）～式（24）则由本文首次给出，适用于0≤r0＜r2-r1的情形。另外，式（19）及式（22）的解析延拓亦适用于轴向参数重叠的情形，即当r2-r1＜r0＜r1＋r2时它们的实部均收敛于积分式（1）的值。

2 对以上结果的渐近处理

为了加快平行轴圆柱线圈的互感积分求积速度，已得到含有变形Bessel函数和变形Struve函数的互感积分表达式。然而在大多数通用数值计算软件（如Matlab、Mathematica）中，对Struve函数Hn（x）和变形Struve函数Ln（x）并未进行优化处理。为了进一步提高互感积分的数值计算速度，现对式（10）～式（12）中引入的函数u、v和w进行渐近近似。

若x≥0，则对x→∞有[9]

当ν＝n，n为整数时，有[9]

因此

从而得到当k→∞时

同理，当k→∞时可得

类似地，可由x→∞时

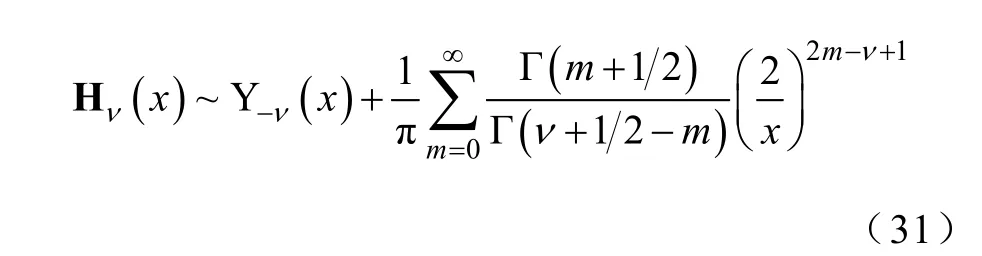
得到当k→∞时

式（29）、式（30）和式（32）中的级数收敛很快，取前p项时，余项误差为，n＝0,1。在以下对第1节推出的广义积分进行数值求积时，对被积参数k较大的区间可由式（29）、式（30）和式（32）对被积函数中的u、v和w进行代换。这一渐近处理将使数值计算速度进一步提高并保证所需计算的准确度。

3 数值计算

式（7）～式（9）的正确性已被文献[7]中的实验所证实，故此处不再对其进行验证。首先对平行轴圆盘线圈互感公式（13）～式（15）进行数值验证。计算平台为CPU工作频率3.4GHz的个人计算机。两线圈参数取为：R1＝0.5m，R2＝1m，R3＝1.5m，R4＝2m，该计算将对归一化互感值M/（N1N2）实行。计算时令渐近展开式中p＝9。结果见表2。ta、tb分别为文献[5]方法和本文所述方法得出表2第三列同一结果时的计算耗时。由该表可见本文所述方法在绝大多数情况下比文献[5]方法快，在r0较大的情况下可比文献[5]方法快1个数量级。另外，表2也显示在r0较小而z0较大的情形，文献[5]方法更为适用，因在此种情形文献[5]中公式所含因子e-kz0将迅速衰减从而加快数值积分速度。

表2　本文方法与文献[5]中方法对两平行轴圆盘线圈互感的计算性能比较Tab.2 Performance of the mutual inductance for two disk coils of parallel axes evaluated with the proposed method and that in Ref.[5]

（续）

表3　本文方法与文献[5]中方法对两平行轴矩形截面圆柱线圈互感的计算性能比较Tab.3 Performance of the mutual inductance for two short thick coils evaluated with the proposed method and that in Ref.[5]

（续）

接下来验证两平行轴矩形截面圆柱线圈互感表达式（16）～式（18）的正确性。计算如下两线圈间的互感：R1＝0.1m，R2＝0.3m，R3＝0.5m，R4＝0.8m，h1＝0.02m，h2＝0.01m。该计算亦将对归一化互感值M/（N1N2）实行。计算结果见表3。ta、tb分别为文献[5]方法和本文所述方法得出表3第三列同一结果时的计算耗时。另外，式（16）～式（18）的适用参数范围有互相重叠的部分，在这种重叠情形下，ta为含Bessel函数的式（18）的计算耗时，而tb则为含变形Bessel函数的式（16）或式（17）的计算耗时。由该表可见，对径向较厚的扁线圈，本文所述方法在绝大多数情况下比文献[5]中方法快，在r0较大的情况下可比文献[5]中方法快2个数量级。

共面圆环互感闭式解式（19）、式（22）与式（1）的比较见表4。取R1＝1m、R2＝2m。当1m＜r0＜3m时去掉了式（19）或式（22）所得结果的虚部。结果显示本文方法与已有方法的计算结果完全一致，也表明了本文闭式解的解析延拓的正确性。式（19）、式（22）的计算几乎在瞬间完成，因此不需要进一步比较其计算耗时。

表4　本文共面圆环互感闭式解与文献[5]中方法的比较Tab.4 Mutual inductance of the coplanar circular loops evaluated with the proposed method compared to that in Ref.[5]

4 结论

若两平行轴圆柱线圈的径向参数较大而轴向参数较小，则以已有的Bessel函数及Struve函数积分计算其互感时将非常耗时。然而，对于线圈径向参数未重叠的情形，运用变形Bessel函数及变形Struve函数的单调性可以得到一种高速高准确度的互感计算方法，此法特别适用于两线圈的轴间距离大于它们外半径之和（r0＞R2＋R4）的情形。数值计算实例表明，本文所述方法在多数情况下可将计算效率提高1～2个数量级，并保持很高的准确度。若对以上互感积分的被积函数Hn（x）与Ln（x）进行渐近处理，则其数值计算速度可以进一步提高，同时保证很高的计算准确度。另外，本文方法对矩形截面圆柱线圈的互感仅需三个公式即可包括这两个线圈之间所有的相对方位，相比而言，文献[5]则需要五个公式。该方法可以视为对已有的圆柱线圈互感计算方法的一个补充，即对于轴向参数较大而径向参数较小的线圈（螺线管），宜采用文献[5]的方法计算互感；而对轴向参数较小而径向参数较大的线圈（圆盘线圈），宜采用本文提出的方法来计算互感。

致谢：Norway Agder University的J.Conway教授对本文用到的渐近展开式提出了非常宝贵的指导和建议，本文作者在此对其表示衷心的谢意。

参考文献

[1]Raju S,Wu R,Chan M,et al.Modeling of mutual coupling between planar inductors in wireless power applications[J].IEEE Transactions on Power Electronics,2014,29（1）:481-490.

[2]Acero J,Carretero C,Lope I,et al.Analysis of the mutual inductance of planar-lumped inductive power transfer systems[J].IEEE Transactions on Industrial Electronics,2013,60（1）:410-419.

[3]Low Z N,Chinga R A,Tseng R,et al.Design and test of a high-power high-efficiency loosely coupled planar wireless power transfer system[J].IEEE Transactions on Industrial Electronics,2009,56（5）:1801-1812.

[4]卡兰塔罗夫П Л,采伊特林Л А.电感计算手册[M].北京:机械工业出版社,1992.

[5]Conway J T.Inductance calculations for circular coils of rectangular cross section and parallel axes using Bessel and Struve functions[J].IEEE Transactions on Magnetics,2010,46（1）:75-81.

[6]Buchholz H.Elektrische und magnetische Potentialfelder[M].Gottingen:Springer,1957.

[7]Hannakam L.Berechnung der Gegeninduktivitat achsenparalleler Zylinderspulen[J].Archiv für Elektrotechnik,1967,51（5）:141-154.

[8]Hannakam L.Praktische Berechnung der gegeninduktivitat zweier kreisförmigen Leiterschleifen in allgemeiner Lage[J].Archiv für Elektrotechnik,1980,62（1）:351-357.

[9]Abramowitz M,Stegun I.Handbook of mathematical functions with formulas,graphs,and mathematical tables[M].Washington D C:National Bureau of Standards,1972.

[10]Conway J T.Analytical solutions for the self-and mutual inductances of concentric coplanar disk coils[J].IEEE Transactions on Magnetics,2013,49（3）:1135-1142.

[11]Yao Luo,Chen Baicao.Improvement of selfinductance calculations for circular coils of rectangular cross section[J].IEEE Transactions on Magnetics,2013,49（3）:1249-1255.

[12]Babic S,Sheppard S,Akyel C.The mutual inductance of two thin coaxial disk coils in air[J].IEEE Transactions on Magnetics,2004,40（2）:822-825.

[13]Conway J T.Inductance calculations for noncoaxial coils using Bessel functions[J].IEEE Transactions on Magnetics,2007,43（3）:1023-1034.

[14]罗垚,陈柏超,袁佳歆，等.倾斜轴空心矩形截面圆柱线圈互感计算[J].电工技术学报,2012,27（5）:132-136.Luo Yao,Chen Baichao,Yuan Jiaxin，et al.Mutual inductance calculations of inclined axial air-core circular coils with rectangular cross-sections[J].Transactions of China Electrotechnical Sosiety,2012,27（5）:132-136.

[15]罗垚,陈柏超.空心矩形截面圆柱线圈自感计算的新方法[J].电工技术学报,2012,27（6）:1-5.Luo Yao,Chen Baichao.New method for selfinductance calculations of air-core circular coils with rectangular cross-sections[J].Transactions of China Electrotechnical Sosiety,2012,27（6）:1-5.

[16]Haas H.Ein Beitrag zur Berechnung der Gegeninduktivität koaxialer Zylinderspulen[J].Archiv für Elektrotechnik,1975,57（1）:21-26.

[17]Babic S,Sirois F,Akyel C,et al.Mutual inductance calculation between circular filaments arbitrarily positioned in space:alternative to Grover’s formula[J].IEEE Transactions on Magnetics,2010,46（9）:3591-3600.

[18]Watson G N.A Treatise on the theory of bessel functions[M].Cambridge,U.K.:Univ.Press,1944.

[19]Prudnikov A P,Brychkov Y A,Marichev O I.Integrals and series[M].New York:Gordon and Breach,1992.

罗 垚 男，1983年生，博士后，主要研究方向为电磁场解析计算。

E-mail:ostpreussen@qq.com（通信作者）

New Approach for the Mutual Inductance Calculations of the Circular Coils with Parallel Axes

Luo Yao
（School of Power and Mechanical Engineering Wuhan University Wuhan 430072 China）

AbstractA method for calculating the mutual inductance of circular coils with parallel axes is presented by using the modified Bessel and modified Struve functions,which is obtained by the expansion expressions of the reciprocal distance in the cylindrical coordinates.The obtained expressions are further coped with the asymptotic expansions to facilitate the numerical calculations.The monotonicity of the modified Bessel and Struve functions is beneficial to the numerical evaluations of the improper integral,especially in the case of short thick coils or disk coils with large radial distance and small axial distance.The proposed method is several tens to hundreds times faster than the existing method using the oscillatory Bessel and Struve functions,with the same accuracy.Additionally,a closed-form solution of the mutual inductance for coplanar circular loops is given using the Gauss hypergeometric functions,and it is verified by numerical calculations.

Keywords：Mutual inductance,modified Bessel functions,asymptotic expansion

作者简介

收稿日期2014-01-03 改稿日期 2014-04-21

中图分类号：TM12；TM153