能量有效的认知多小区协同波束赋形算法

张秀秀,陈东华,谢维波

(1.华侨大学信息科学与工程学院,福建厦门 361021;2.华侨大学计算机科学与技术学院,福建厦门361021)



能量有效的认知多小区协同波束赋形算法

张秀秀1,陈东华1,谢维波2

(1.华侨大学信息科学与工程学院,福建厦门 361021;2.华侨大学计算机科学与技术学院,福建厦门361021)

摘要：针对认知多小区多用户下行传输链路,提出了一种基于能量效率最大化准则的协同波束赋形优化方法.该方法采用迫零消除小区内用户间干扰,在保证用户最小速率需求及认知干扰约束的同时,实现了能量效率和频谱效率的同步改善.为了分布式求解优化问题,通过约束泄露干扰并利用半定松弛,将其转换为凸问题,在此基础上,采用部分对偶分解方法将多小区联合优化问题分解为一组单小区优化问题,从而实现了分布式求解.仿真结果表明,该方法不仅实现了能量效率和频谱效率的有效折中,而且达到了集中式算法的性能.

关键词:认知多小区;波束赋形;能量效率;对偶分解;凸优化

1引言

随着无线通信业务的迅速发展,无线频谱资源的供需矛盾日益凸显.为了解决这一问题,认知无线电技术[1]受到广泛的关注.认知无线电网络通过动态频谱接入,充分利用现有网络频谱资源,极大提高了频谱利用率,已被多种标准如IEEE 802.22、IEEE 802.16h标准所采纳.另一方面,多小区协同波束赋形通过协调小区间传输可以有效抑制小区间干扰.两者相结合,不仅能够充分利用空域资源,进一步提高频谱利用率,而且可以有效抑制系统中的干扰.

针对多小区波束赋形问题,国内外学者进行了广泛研究,然而大多研究只追求频谱效率最大化[2～6],却忽视了系统的能量效率.近来,随着高数据速率应用业务的快速增长,能量损耗急剧增加,导致运营成本增加,温室气体排放量增大,因此,如何设计协同波束赋形矢量从而实现能量效率与频谱效率的折中,成为未来通信得以持续发展的关键.文献[7,8]研究了以最大化能量效率为目标的波束赋形优化问题;文献[9]研究了多小区高能效联合波束赋形与功率分配问题,根据用户速率与最小均方误差之间的关系,提出了一种复杂度低、回程开销低的迭代优化算法;文献[10]设计了一种基于能量效率最大化准则的多小区协作预编码方案,该方案将非线性非凸问题转化成多项式优化问题,并用KKT条件求解非凸问题;在给定速率约束下,文献[11]和[12]分别提出了具有QoS(Quality of Service)保障的多小区能效最大化波束赋形方法;同样在给定速率约束下,文献[13]以每宏小区干扰泄露为约束、以最大化每宏小区能效函数之和为目标,提出了一种异构网络中的波束赋形方法.上述关于能量效率优化问题的研究均未考虑认知框架或者无法直接推广至认知多小区场景,在认知系统中,认知用户通过动态频谱检测,获取可利用的授权频谱资源,在提高频谱利用率的同时增加了系统的能耗,因此,在认知场景下,基于能量效率最大化准则的协同波束赋形方法尤为重要,然而当前这方面的应用还未得到有效解决.

针对认知多小区应用,本文以文献[6]为基础提出了一种协同波束赋形算法.与文献[6]不同,本文方法是在多小区多用户场景下以最大化认知系统的能量效率为目标,同时考虑认知用户传输速率约束,从而一方面改善了系统能量效率,另一方面满足了用户最小QoS要求.由于速率约束导致优化问题非凸,采用泄露干扰约束和半定松弛将其转换为凸半正定规划问题,在对偶框架下提出了优化问题的分布式求解方法.

符号说明:(·)*和(·)H分别表示矩阵的共轭和共轭转置,Tr(A)、Rank(A)为矩阵A的迹和秩,A0 表示矩阵A为半正定矩阵,E[·]表示统计均值,max表示取最大值.

2系统模型

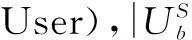
认知小区b中第k个SU的接收信号可写为

(1)

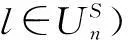
由于在频率复用因子为1的多小区系统中,相比小区间干扰,小区内用户间的干扰更为严重,因此我们提出采用迫零方案消除小区内用户间干扰、采用干扰协调来抑制小区间干扰的方法,即小区内波束赋形矢量应满足

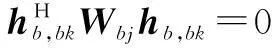
(2)

(3)

定义SBSb到PU的传输信道矢量为gb∈CT×1,则PU接收到的来自所有SBS的总干扰可表示为

(4)

系统的能量效率定义为系统总速率与消耗总功率之比[8],其数学表达式为

(5)

为了保证SU所需的服务质量,本文以SU的传输速率为约束,以系统的能量效率最大化为目标,同时考虑认知干扰约束构造如下优化模型(Problem 1:P1)

(6a)

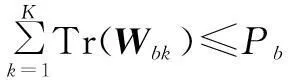
(6b)

(6c)

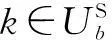
(6d)

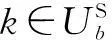
(6e)

Wbk0,∀b∈B,∀

(6f)

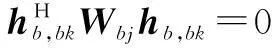
(6g)

其中,Pb为SBSb所允许的最大发射功率,Ith表示PU正常通信所允许的最大干扰值,rbk为认知小区b中SUk所需的最小传输速率.

3认知多小区协同波束赋形问题求解

由能量效率的定义式(5)不难看出,优化目标为非线性非凸函数,从而导致优化问题P1为非凸问题,难以得到其最优解.为了求解这一问题,本节通过引入参数规划、干扰泄露约束及半正定松弛将P1转化为凸优化问题,集中式求解需要一个能获得各小区相关信息的中心控制单元,从而增大了实现复杂度.为此,我们采用对偶分解理论,将多小区联合波束赋形问题分解为一组单小区波束赋形问题,从而实现了分布式求解,避免了集中式算法的缺点.接下来首先采用集中式方法求解优化矢量,然后利用分布式优化方法解决这一问题.

3.1集中式算法

为了求解非凸问题,首先通过参数规划[8]将非线性参数规划问题改写为与之等效的单变量方程,引进参数γ,则优化问题(6)等价为

F(γ)=0

(7)

式中,F(γ)定义为

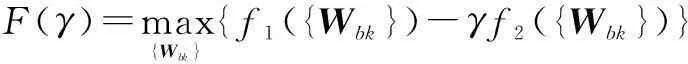
F(γ)=max{Wbk}{f1({Wbk})-γf2({Wbk})}

(8)

s.t.式(6b)～(6g)

由参数规划原理[14,15]可知,如果能找到一个特定的参数γ*,使得F(γ*)=0成立,那么满足F(γ*)=0的波束赋形矩阵即为优化问题(6)的最优解.

基于上述事实,我们可以发现,问题(6)的求解等效于在参数γ*已知的条件下求解问题(8).由于F(γ)是单调递减函数,且F(γ)=0有唯一解,因此可利用二分搜索法迭代优化参数γ并输入到优化问题式(8)进行求解,直至搜索到最优的参数γ*.为简化起见,给定参数γ时,问题(8)可写为(Problem 2:P2)

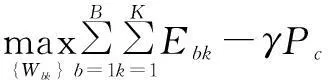
max{Wbk}∑Bb=1∑Kk=1Ebk-γPc

(9)

s.t.式(6b)～(6g)

式中:Ebk=Rbk({Wbk})-γTr(Wbk).

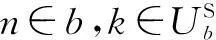
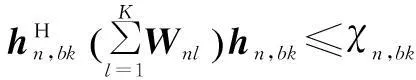
(10)

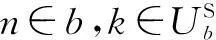
(11a)

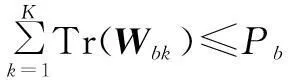
(11b)

(11c)

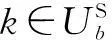
(11d)

Wbk0,∀b∈B,∀

(11e)

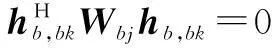
(11f)

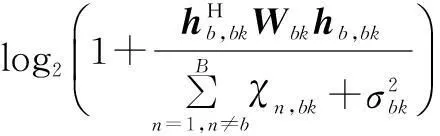
(11g)

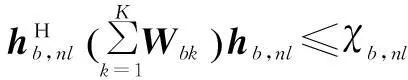
(11h)

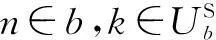
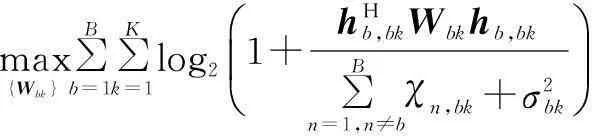
max{Wbk}∑Bb=1∑Kk=1log21+hHb,bkWbkhb,bk∑Bn=1,n≠bχn,bk+σ2bkæèççöø÷÷

(12)

s.t.式(11b)～(11h)

利用对数函数的性质将约束式(11g)转换为如下线性约束

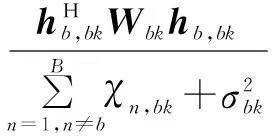
(13)

将速率约束写成式(13)以后,P2变为如下优化问题(P3)

(14a)

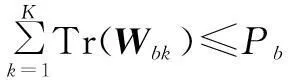
(14b)

(14c)

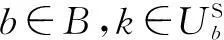
(14d)

Wbk0,∀

(14e)

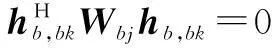
(14f)

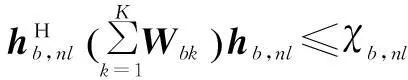
(14g)

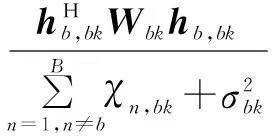
(14h)

秩1约束(式(14d))导致P3的非凸性,松弛秩1约束,则P3变为半正定规划问题,从而可用数值算法[16]或凸优化软件CVX[17]求解.得到优化解Wbk后,从中提取秩1解就可得到优化矢量wbk.

3.2分布式算法

上一节提出了一种集中式算法,但其实现需要一个中心控制单元,每个SBS需要通过回程链路(Backhaul)将其信道状态信息发送至中心控制单元,中心控制单元完成计算以后再通过回程链路将计算结果传递给各个SBS,从而增大了实现复杂度和回程开销.为了简化系统实现,本节提出一种分布式优化算法.由优化问题P3的约束可以看出,不同SBS的波束赋形矢量仅通过认知干扰约束(式(14c))耦合在一起,恰好符合对偶分解理论[18].接下来,我们采用对偶分解来分布式处理上述优化问题.引入拉格朗日乘子η,则秩1松弛后的优化问题式(14)的部分拉格朗日函数可写为

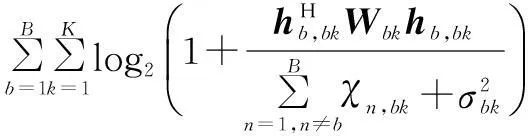
(15)

s.t. 式(14b),式(14e),式(14f),式(14g),式(14h)

通过对偶分解,可将秩1松弛后的P3分解成B个子问题和一个主问题,子问题独自求解优化变量,主问题通过基站间协作求解.第b个子问题为

(16a)

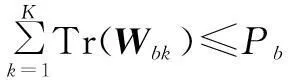
(16b)

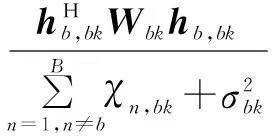
(16c)

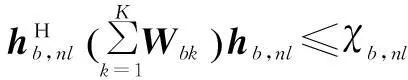
(16d)

Wbk0,∀

(16e)

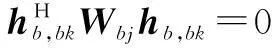
(16f)

拉格朗日乘子η给定时,式(16)为凸优化问题,可采用数值算法或凸优化软件求解.对偶主问题为

(17)

s.t.η≥0

其中,Db(η)为η给定时,对应于第b个优化子问题式(16)的对偶函数

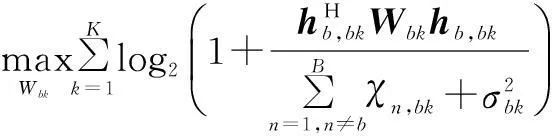
(18)

s.t.式(16b)～(16f)

主问题可由次梯度法得到.次梯度法迭代求解公式为

(19)

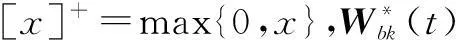
由于秩1松弛后的P3为凸问题,且满足强对偶性,因此分布式求解优化问题与集中式求解所得的结果是相同的;同时,由于子问题式(16)为凸问题,存在唯一解,从而保证了分布式算法的迭代收敛性.完整的认知多小区分布式协同波束赋形算法步骤如下:

(1)初始化参数γmin=0,γmax=0且满足F(γmax)<0,F(γmin)>0;

(2)设参数γ=(γmin+γmax)/2;

(3)令t=0,初始化η(0);

(4)对于每个认知小区,利用步骤(2)的γ值,求解子问题式(16);

(5)根据式(19)更新拉格朗日乘子η;

(6)若满足收敛条件|η(t)-η(t-1)|<ε(ε为充分小的正数),则转至步骤(7);否则t=t+1,返回步骤(4);

(7)利用式(8)计算F(γ),若F(γ)>0,则令参数γmin=γ;否则令参数γmax=γ;

(8)如果满足|γmax-γmin|<ζ(ζ为充分小的正数),则转至步骤(9);否则转至步骤(2);

(9)由{Wbk}提取波束赋形矢量{wbk};

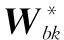
4仿真分析

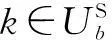
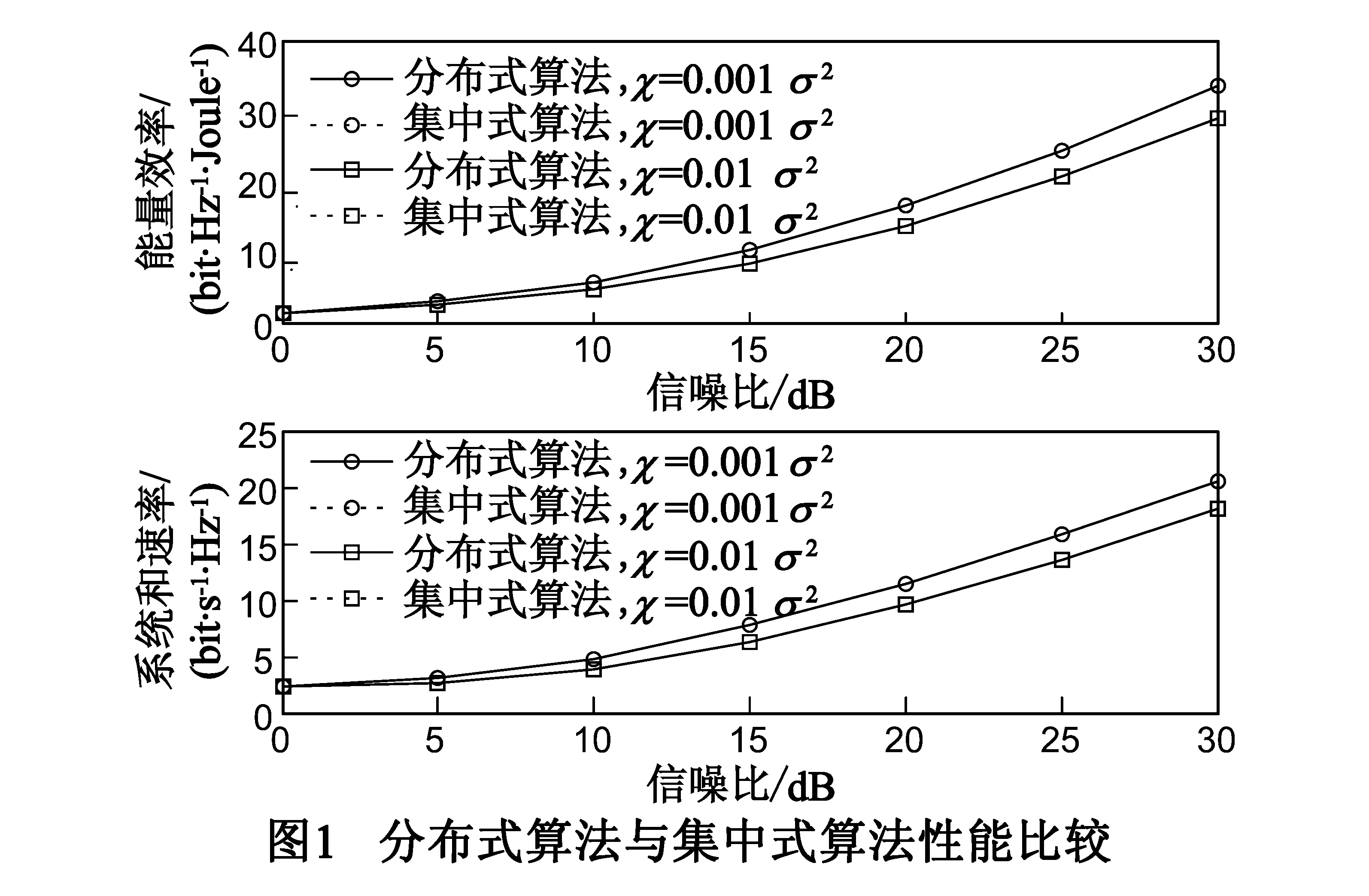
图1给出了分布式算法与集中式算法的性能比较曲线.由图可见,分布式算法与集中式算法对应的性能曲线基本一致,这也验证了对偶分解的有效性.观察图1还可以发现,随着认知用户SNR的增加,系统的能量效率及系统和速率也随之增加.由图1还可看出,两种泄露干扰门限下,系统实际取得的速率均满足速率约束,在泄露干扰门限为0.01σ2,SNR=0dB的时候,系统和速率为2.3bit/s/Hz左右,每个认知用户平均速率为0.575bit/s/Hz左右,高于给定的速率约束(0.5bit/s/Hz);同时我们可以发现在低信噪比区域,增大泄露干扰门限,对系统性能影响较小;在高信噪比区域,泄露干扰门限越大,系统的能量效率及系统和速率越小,这是由于信噪比高的时候,小区间干扰成为影响系统性能的主导因素,而在频率复用因子为1的多小区系统中,小区间干扰越大,小区边缘用户的性能越差,从而导致系统性能下降.

在r=0.4bit/s/Hz,干扰泄露门限χ=0.01σ2的情况下,图2仿真了系统和速率随认知用户SNR的变化曲线.图中结果表明,系统和速率随认知用户信噪比的增加而增加,在高信噪比区域,本文所提算法达到的系统和速率要低于最大化系统和速率算法得到的结果,这是因为本文算法为了提高系统的能量效率会最大限度的降低系统的发射功率,从而导致系统和速率降低,而最大化系统和速率算法则通常以最大发射功率传输信号,以此来保证达到系统的最大和速率.观察图2还可以看出,认知干扰门限越小,系统和速率也越小,这是由于认知干扰门限越小,认知系统受到的约束越苛刻,从而限制了系统和速率的增加.

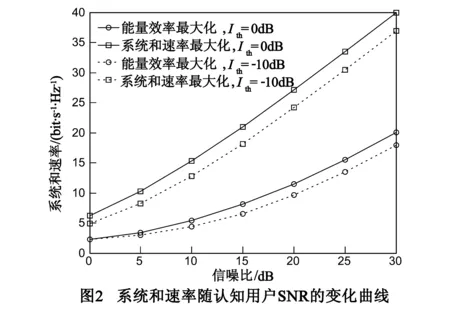
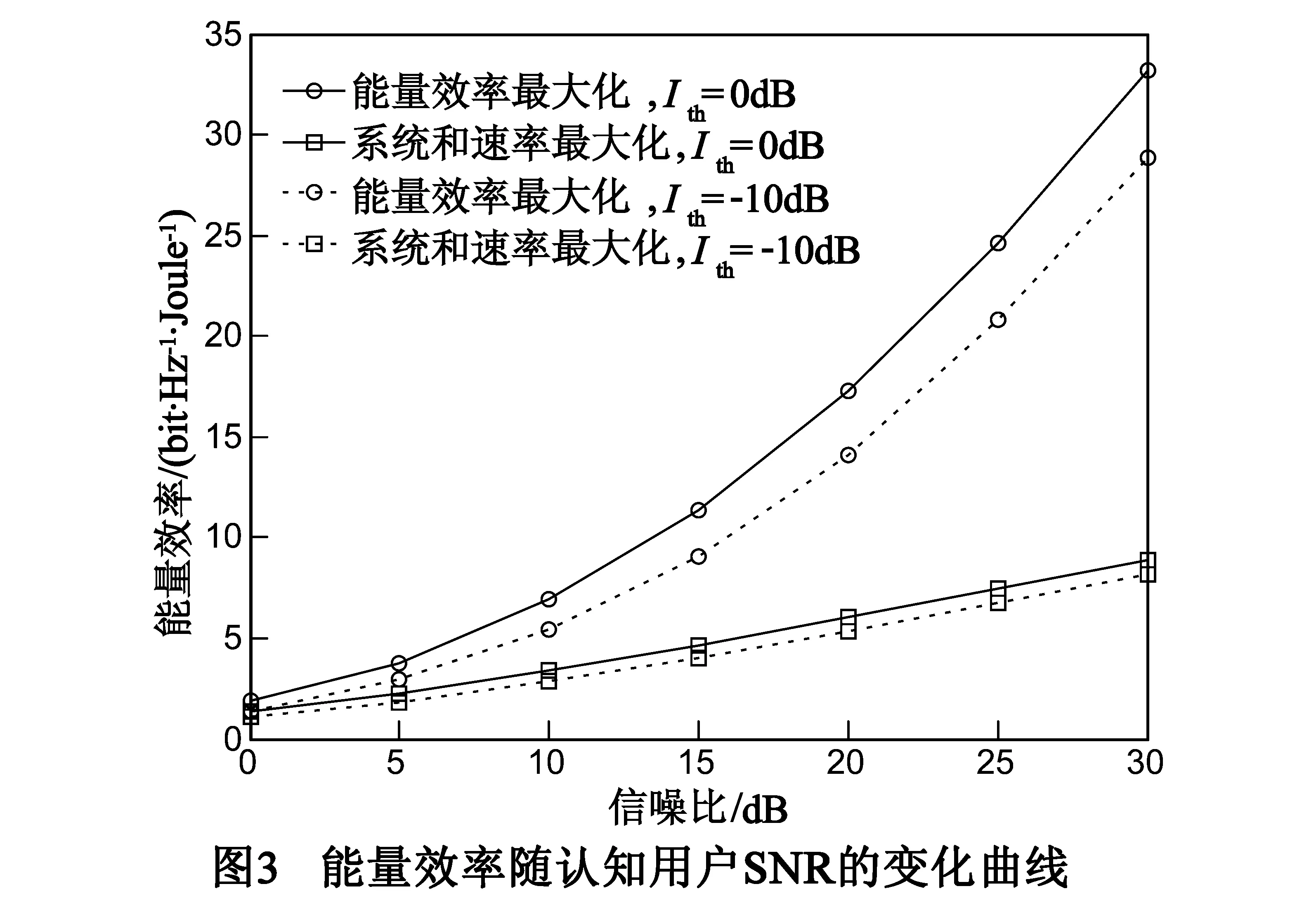
与图2的仿真参数相同,图3给出了能量效率随认知用户SNR变化的性能关系曲线.由仿真结果可见,系统能量效率随着认知用户SNR的增大逐渐增加,并且能量效率的增长趋势也是增加的.在高信噪比区域,本文算法达到的能量效率要高于系统和速率最大化算法达到的能量效率.观察图3还可以发现,认知干扰门限越大,系统的能量效率越高.

综合图2、图3可以发现,仿真参数相同的情况下,在高信噪比区域,以系统和速率为优化目标的算法虽然达到了最大速率,但却过分牺牲了系统的能量效率.本文算法以能量效率为优化目标,牺牲了两倍左右的速率,但却换来了接近四倍的能量效率,从这个意义上看,本文算法要优于系统和速率最大化算法,实现了能量效率和频谱效率的有效折中.

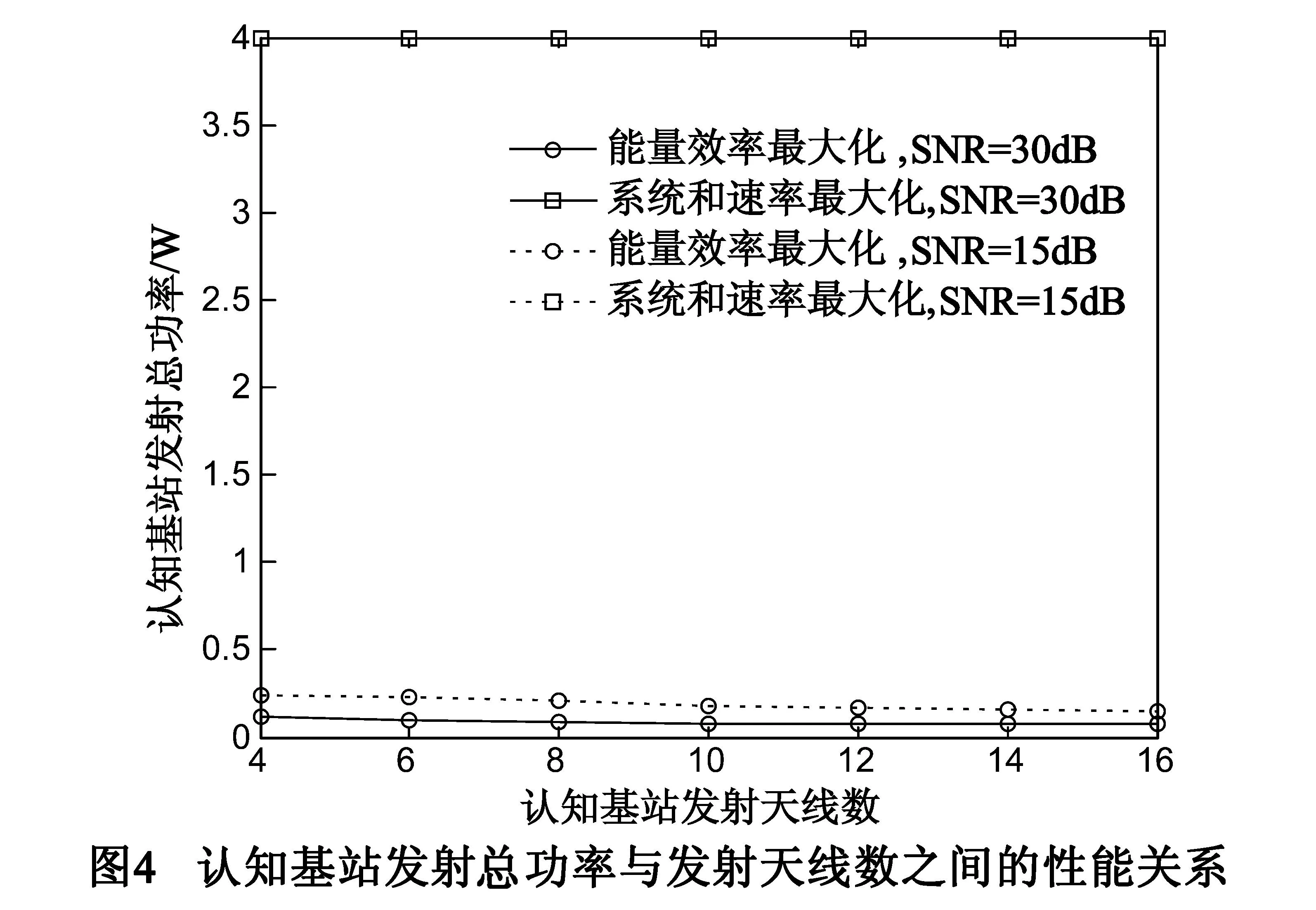
在r=1bit/s/Hz,干扰泄露门限χ=0.01σ2的情况下,图4给出了发射天线数与认知基站发射总功率之间的性能关系.由图可见,本文所提算法的基站发射功率随天线数增加而减少,并且基站发射功率的降低趋势也是减少的.最大化系统和速率算法所需的发射功率基本稳定在最大发射功率,这是由于为了达到最大和速率,系统通常以最大发射功率传输信号.此外,观察图4还可以发现,SNR越高,最大化能量效率算法所需的发射功率越低,不难解释,由于SNR=1/σ2,信噪比越低,噪声越大,对系统性能的影响越大,而通信系统通常采用增加发射功率的方法,来降低噪声对系统性能的影响.Nt=4,SNR=15dB时,本文所提算法的基站发射功率为0.23W左右,远低于系统和速率最大化算法的基站发射功率,进一步验证了本文算法可以有效实现能量效率与频谱效率的折中.

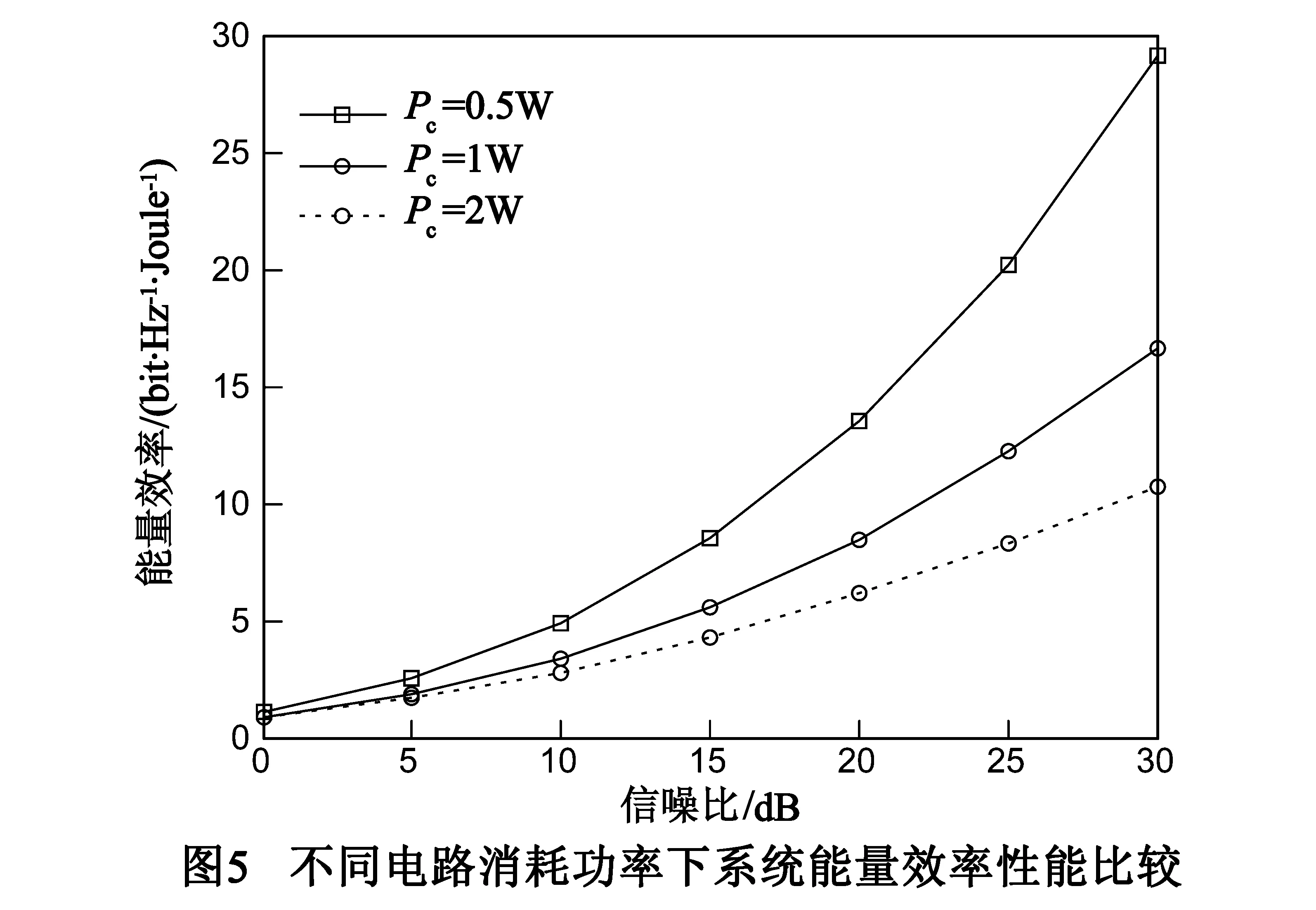
在r=0.5bit/s/Hz,干扰泄露门限χ=0.01σ2的情况下,图5给出了不同电路消耗功率下,能量效率性能比较曲线.由图可见,在低信噪比区域,改变电路消耗功率对系统性能影响较小,在高信噪比区域,系统性能随电路消耗功率的增大而降低,这是因为,信噪比低的时候,噪声为影响系统性能的主导因素,高信噪比时,噪声对系统性能的影响减弱,电路消耗功率对系统性能的影响逐渐体现出来.同时结合能量效率的定义不难发现,在其它参数不变的条件下,电路消耗功率越高,系统能量效率越低.

5结论

依据系统能量效率最大化准则,联合设计了认知多小区多用户协作波束赋形矢量,并利用对偶分解实现了该优化问题的分布式求解.与集中式算法相比,分布式算法只需各小区间交换有限个标量值,避免了大量矢量信息的回程传输.仿真结果表明,提出的算法不仅实现了能量效率和频谱效率的有效折中,而且达到了集中式算法的性能.

参考文献

[1]Haykin S.Cognitive radio:brain-empowered wireless communications[J].IEEE Journal on Selected Areas in Communications,2005,23(2):201-220.

[2]Qiu J M,Zhang R,Luo Z Q,et al.Optimal distributed beamforming for MISO interference channels[J].IEEE Transactions on Signal Processing,2011,59(11):5638-5643.

[3]Komulaine P,Tolli A,Juntti M.Effective CSI signaling and decentralized beam coordination in coordination in TDD multi-cell MIMO systems[J].IEEE Transactions on Signal Processing,2013,61(9):2204-2218.

[4]Zhang R,Cui S G.Cooperative interference management with MISO beamforming[J].IEEE Transactions on Signal Processing,2010,58(10):5450-5458.

[5]Gallo L,Negro F,Ghauri I,et al.Weighted sum rate maximization in the underlay cognitive MISO interference channel[A].Proceedings of the 2011 IEEE 22nd International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC)[C].Toronto,Canada:IEEE,2011.661-665.

[6]Kim Y J,Song M G,Cho Y S,et al.Decentralized beamformer design with limited multi-cell cooperation for interference channel of cognitive radio networks[J].IEEE Transactions on Wireless Communications,2013,12(8):4142-4152.

[7]Huang Y,Xu J,Qiu L.Energy efficient coordinated beamforming for multi-cell MISO systems[A].Proceedings of the IEEE Global Communications Conference (GLOBECOM)[C].Atlanta,Georgia:IEEE,2013.2526-2531.

[8]Huang Y M,He S W,Jin S,et al.Decentralized energy efficient coordinated beamforming for multicell systems[J].IEEE Transactions on Vehicular Technology,2014,63(9):4302-4314.

[9]He S W,Huang Y M,Jin S,et al.Coordinated beamforming for energy efficient transmission in multi-cell multiuser systems[J].IEEE Transactions on Communications,2013,61(12):4961-4971.

[10]He S W,Huang Y M,Yang L X,et al.Coordinated multicell multiuser precoding for maximizing weighted sum energy efficiency[J].IEEE Transactions on Signal Processing,2014,62(3):741-751.

[11]Wang X M,Zhu P C,Sheng B,et al.Energy-efficient downlink transmission in multi-cell coordinated beamforming systems[A].Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC)[C].Shanghai,China:IEEE,2013.2554-2558.

[12]Xu Z K,Yang C Y,Li G Y,et al.Energy-efficient CoMP precoding in heterogeneous networks[J].IEEE Transactions on Signal Processing,2014,62(4):1005-1010.

[13]He S W,Huang Y M,Wang H M,et al.Leakage-aware energy efficient beamforming for heterogeneous multicell multiuser systems[J].IEEE Journal on Selected Areas in Communications Special Issue in 5G Communication Systems,2014,32(6):1268-1281.

[14]Jagannathan R.On some properties of programming problems in parametric form pertaing to fractional programming[J].Management Science,1966,12(7):609-615.

[15]Dinkelbach W.On nonlinear fractional programming[J].Bulletin of the Australian Mathematical Society,1967,13(7):492-498.

[16]Boyd S,Vandenberghe L.Convex Optimization[M].Cambridge,UK:Cambridge University Press,2004.655-656.

[17]Grant M,Boyd S.CVX:Matlab Software for Disciplined Convex Programming,version 1.21[EB/OL].http://cvxr.com/cvx/,2010.

[18]Palomar D P,Chiang M.A tutorial on decomposition methods for network utility maximization[J].IEEE Journal on Selected Areas in Communications,2006,24(8):1439-1451.

张秀秀女,1988年9月出生于河南濮阳,华侨大学硕士研究生,主要研究方向为协作多点传输技术管理.

E-mail:292573449@qq.com

陈东华(通信作者)男,1977年6月出生于安徽濉溪,博士,副教授,主要研究方向为宽带无线通信、无线网络资源管理.

E-mail:dhchen0@163.com

谢维波男,1964年10月出生于福建泉州,现为华侨大学教授,主要研究方向为智能信号与信息处理、图像处理、无线移动自组织网络等.

E-mail:xwblxf@ hqu.edu.cn

Energy Efficient Coordinated Beamforming for Cognitive Multi-cell Systems

ZHANG Xiu-xiu1,CHEN Dong-hua1,XIE Wei-bo2

(1.CollegeofInformationScienceandEngineering,HuaqiaoUniversity,Xiamen,Fujian361021,China;2.CollegeofComputerScienceandTechnology,HuaqiaoUniversity,Xiamen,Fujian361021,China)

Abstract:A cooperative beamforming algorithm based on the maximize of energy efficiency(EE) was proposed for the cognitive multi-cell multiuser downlinks.By using zero-forcing algorithm to eliminate intra-cell interference,the proposed scheme makes a simultaneous improvement in energy efficiency and spectrum efficiency(SE) while guaranteeing minimum rate for the secondary users and the cognitive interference constraints. To implement a decentralized algorithm,the original problem was firstly transformed to a convex one via semi-definite relaxation and the leakage interference constraints,and then was decomposed into a group of sub-problems on the basis of each cell by using dual decomposition,which admits a distributed computation of the problem.Simulation results show that the proposed scheme not only makes a good tradeoff between the EE and SE,but also attains the same performance as the centralized algorithm.

Key words:cognitive multi-cell;beamforming;energy efficiency;dual decomposition;convex optimization

作者简介

DOI:电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.03.033

中图分类号:TN929.5

文献标识码：A

文章编号：0372-2112 (2016)03-0718-07

基金项目:国家自然科学基金(No.61271383)

收稿日期:2014-09-01;修回日期:2015-01-30;责任编辑:覃怀银