新课标下向量学习的问题分析及数学建议



新课标下向量学习的问题分析及数学建议

◇甘肃杨海年

向量是数学中最基本、最重要的概念,主要用于解决证明线线、线面垂直及计算线线角等问题,利于学生理解,也有助于学生自己想象,为解题带来很大的方便．

1向量学习中存在的问题

向量具有代数形式与几何形式2种身份,这也就决定了向量能够帮助学生理解数学运算的意义,提高逻辑思维能力,进而建立学生的数学思维．但是在实际教学中,很大一部分学生觉得向量很抽象,因此在学习向量过程中存在许多的问题．

1.1很少向学生介绍向量的历史

很多教师虽然对向量发展的历史比较了解,但是在教学中,由于受到很多原因的影响,教师鲜有提及向量发展的历史,使得学生对于向量这一知识点所代表的数学文化不了解,因此不能深入地理解向量的含义．

1.2不重视向量基础概念的讲解

很多教师觉得向量这一章知识很简单,对于课本中出现的一些基础概念只是一带而过，甚至叫学生自己读一遍．这种不注重理解概念深层含义的做法，最终导致了学生只是机械地背概念、记公式、练习题．如果学生对概念不理解,就不能灵活地运用这些概念,最后解题的质量也大打折扣．

1.3对向量的研究性课题关注不够

在新课标的课本中有很多的研究性课题,但是大部分教师由于课时或者自身科研水平限制,很少会带领学生学习研究这些课题,学生不能形成科研意识,也不能亲身体验研究的乐趣,这将是他们学习过程中很大的遗憾．

2对向量的教学建议

2.1注重向量的文化价值教学

数学有漫长的历史,当然也有丰富的文化底蕴,教师在平时的教学中应该向学生灌输向量的文化价值,让学生对向量的产生、发展、研究与应用有很深刻的了解,这样才能激发学生浓厚的学习兴趣．

2.2注重基础教学

新课标一直要求重视“双基”教学,试想一个人还不会走，怎么让他跑呢?学生还没有理解基础概念,怎么能够灵活应用其解题呢?因此教学中要立足教材,认真阅读教材中出现的基础概念,提高学生将几何问题转化为向量问题的能力．

2.3注重向量运用,形成数学思维

向量是现代数学的基础,是数与形有效转化的工具.因此教学中教师应深入挖掘公式、定理以及习题中向量运用问题,让学生逐渐形成向量意识,领悟向量作为解题工具所具有的特殊价值．同时注意数形结合、化归转化与分类讨论等数学思维的灌输．

1) 向量与代数式之间的转化．

这样一道代数题目,如果用传统的方法来解很复杂,若转化为向量的问题,建立合适的坐标系,问题就会变得简单.

这道题中一共有6个变量,但是却只给了3个方程式,肯定是解不出来的,如果利用向量积来解题,很容易能出结果.

所以 cos〈a,b〉=1,即向量a、b共线且同方向.

2) 向量与三角函数之间的转化．

在学习三角函数时,需要理解并且记忆很多的概念以及公式,但是很多时候并不能熟练地运用这些公式,导致了三角函数题的失分率很高.用向量同样能解决此类问题．

本题既可以用三角函数来解决,也可以设2个向量来巧妙地解决．

解法2可设 a=(7,24),b=(sinα,cosα),则已知可转化为a·b=7sinα+24cosα=25.又因为

a·b=|a||b|cos〈a,b〉=25, |a|=25, |b|=1,

观察上面2种解法：解法1是传统方法,很容易想到,但计算复杂,容易出错. 解法2需要对向量的概念深层次把握,要学会将向量作为一种工具来使用,这对解题人的数学思维有很大的考验．

由此可见,向量作为一种工具性解决手段真的很重要,也需要花很多精力来锻炼数学思维．

3) 向量与几何的转化．

几何的题目中有平面几何、解析几何以及立体几何,这3种几何都可以用向量的方法来解题．

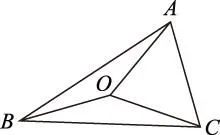
图1

必要性： 如图1,若点O是△ABC的外心,则点O在线段AB的垂直平分线上,则

因为向量也具有几何的性质,所以在求解解析几何问题时，很多情况下都能用到向量.比如在平面几何中用于三角形的“四心”证明.解析几何把代数与几何结合起来,这样就需要向量这个具有桥梁作用的工具用来解决一些二者结合的题目,比如某点的轨迹方程.除此以处，立体几何是向量运用最多的题目,因为向量能够解决立体几何中的点、线、面问题,所以向量的重要性可想而知．

在向量的教学中,教师要转化思维,带领学生积极参与,学生要发挥学习的主观能动性,形成数学能力与数学思维．总之,兼具应用价值与工具性价值的向量值得研究．

(作者单位：甘肃省民乐县第一中学)