高中数学中转化思维的应用分析



高中数学中转化思维的应用分析

◇河北王丙亮

随着教学改革不断深入,高中数学命题方式也更加偏向对学生思维方式、解题方法的考查.很多题目中都需要运用到各种数学解题思维,因此在高中数学课堂上,教师应该教会学生如何运用各种解题思维解决大量的实际问题,提高数学成绩．转化思维在高中数学解题过程中十分常见,本文以转化思维在解题中的转化方式进行例析．

1分与合的转化

分与合的转化思维是指将数学题目中很多隐含的关系挖掘出来,或者将已知条件与结论进行重新组合或者改造,将一些零散的信息整合在一起,进而得到有利于解题的新条件．

分析已知条件中的角分别为2α+β和β,函数为正弦函数.结论需要证明的是正切函数,同时2个角也不同,分别是α+β和α.已知条件与结论中的角并不同,此时就需要运用转化思维.仔细审题之后发现2α+β=(α+β)+α,β=(α+β)-α,在明确了这一点之后,通过两角之和与差的正弦公式证明.

证明因为sin(2α+β)=4sinβ，所以

sin[(α+β)+α]=4sin[(α+β)-α].

sin(α+β)cosα+cos(α+β)sinα=

4sin(α+β)cosα-4cos(α+β)sinα,

3sin(α+β)cosα=5cos(α+β)sinα.

两边同时除以cos(α+β)cosα可得到3tan(α+β)=5tanα，所以3tan(α+β)=5tanα.

2正与反的转化

正与反的转化思维是指从正常思维的反面去进行分析和解决问题,在高中数学中,很多题目运用正向思维很难解决,或者是很难快速解决,如果转化一下思维,从问题的相反方向去考虑,困难往往迎刃而解,思维也豁然开朗．

所以

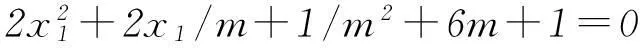
3数与形的转化

“数”与“形”转化思维是培养学生数学思维的最有效方式.教师必须要让学生明白,它并不是单纯的将“数”转变为“形”,而是要进行双向转换,不能只有代数的思想,而没有图形的直观,也不能只有直观的形,而缺乏数据的分析．只有做到“数”与“形”的有机融合,才能够达到解题的目的．

图1

转化思维的应用渗透在高中解题的各个环节中,可能在最后得出结论时进行转化,也可以是在分析问题的过程中进行转化.教师在讲解的过程中,要做到科学引领,帮助学生掌握正确使用这些思维方法,最大限度地提升学生理论联系实际的能力,能够运用转化思维解决更多的实际问题．本文以转化思维中常见的3种思维方式进行例题分析,希望能够为同行提供一些建议和参考．

(作者单位：河北省沧州市第二中学)