两两NQD阵列加权和的LP收敛性

宋明珠， 吴永锋， 向亚云

(铜陵学院 数学与计算机学院， 安徽 铜陵 244000 )



两两NQD阵列加权和的LP收敛性

宋明珠， 吴永锋， 向亚云

(铜陵学院 数学与计算机学院， 安徽 铜陵 244000 )

摘要：研究了两两NQD阵列加权和的Lp收敛性，在更弱的条件下得到与陈平炎相同的结论，改进和推广了前人的研究成果.

关键词：两两NQD阵列； 加权和； Lp收敛性

SONG Mingzhu, WU Yongfeng, XIANG Yayun

(InstituteofMathematicsandComputing,TonglingUniversity,Tongling244000,AnhuiProvince,China)

1引言和引理

两两NQD (Negatively Quadrant Dependend)列的概念是由统计学家LEHMANN[1]于1966年提出，其定义如下：

定义1若∀x,y∈R,都有

P(X≤x,Y≤y)≤P(X≤x)P(Y≤y),

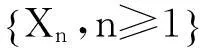
两两NQD列是一类非常广泛的随机变量序列，著名的NA序列[2]、LNQD序列[3]都是其特殊情况，因此对两两NQD列的研究显得更为迫切.两两NQD列极限理论的研究已取得了一些成果，详见文献[4-11].

定义2若

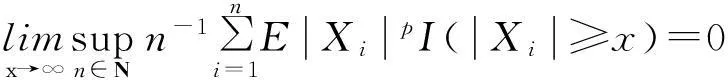
文献[7]在2阶Cesàro一致可积的条件下，得到了两两NQD列的Lp收敛性.文献[8]在p(1≤p<2)阶Cesàro一致可积的条件下，得到了与文献[7]相同的结果.

本文在更弱的条件下得到与文献[8]相同的结论，改进和推广了前人的研究成果.

引理1[1]设随机变量X和Y是NQD的，则

(1)EXY≤EXEY;

(2) 对∀x,y∈R,都有

P(X>x,Y>y)≤P(X>x)P(Y>y);

(3) 如f,g同为非降(或非增)函数，则f(X)与g(Y)仍为NQD的.

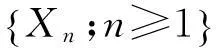
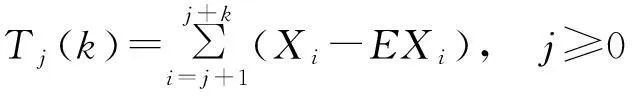
则有

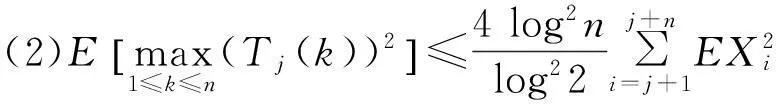
2主要结果及证明

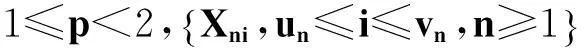
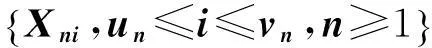
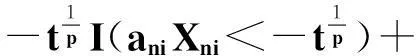
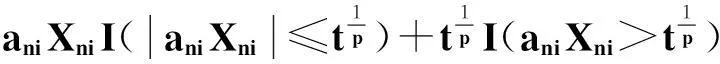
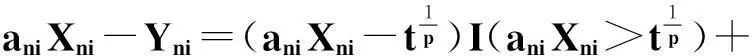
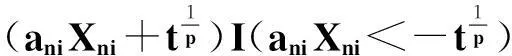
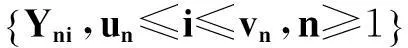
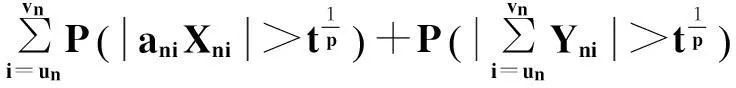
对任意给定的ε>0，有

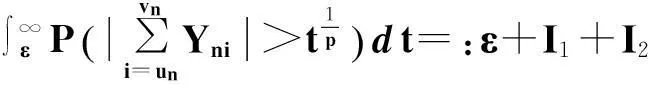
(1)

只须证I1→0,I2→0(n→∞).

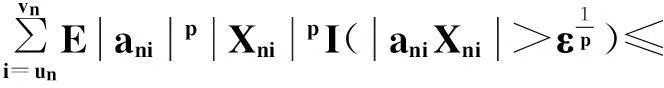
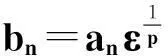
I1→0(n→∞).

(2)

由Zni的定义，知

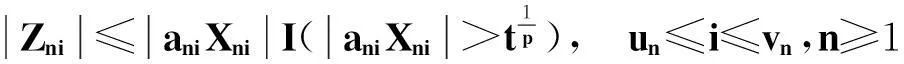
因为EXni=0,所以∀t≥ε,有

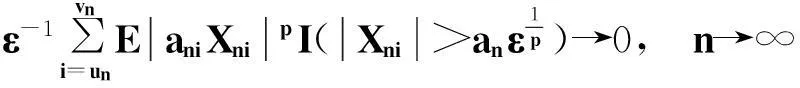
则存在N1∈N,对∀n>N1,t≥ε,有

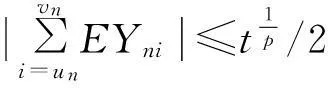
由引理2和Cr-不等式得，对∀n>N1,有

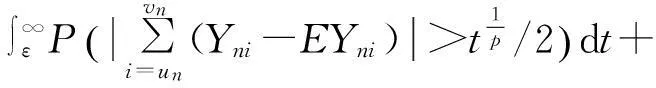
CI1=∶CI3+CI1.

(3)

下证I3→0.

对∀n>N1，t≥ε,有

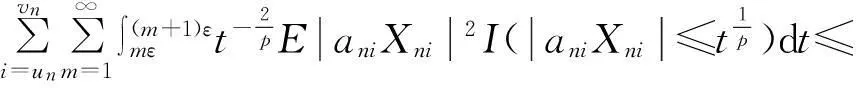
(4)

因为ε是给定的常数，由条件(1)、(2)得

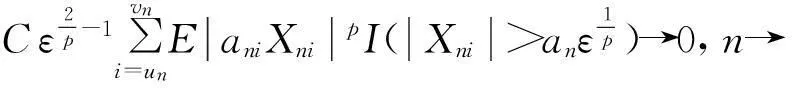
(5)

又因为

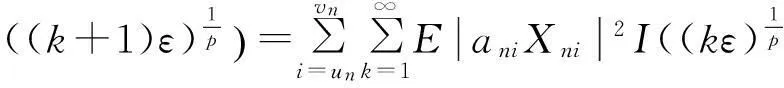
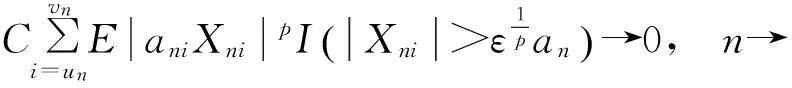
(6)

由式(1)～(6)可得定理1成立.

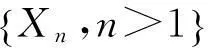
则

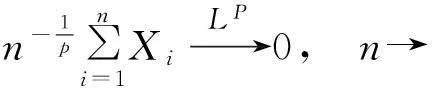
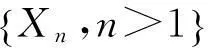
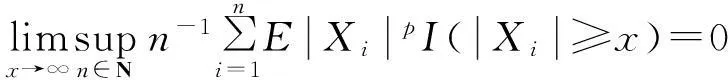
(7)

则

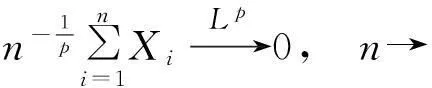
由式(7)可得，对∀ε>0,∃x0>0,

当x>x0时,有

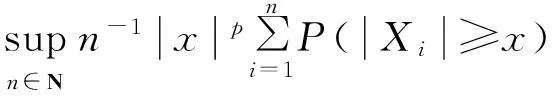
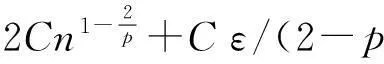
由1≤p<2以及ε的任意性，可得

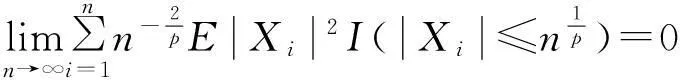
即推论1(ii)成立，由推论1知推论2成立.

注由推论2的证明过程可知，本文在更弱的条件下获得了与文献[8]相同的结论，进而推广并改进了文献[8]的结果.

参考文献(References)：

[1]LEHMAMNEL.Someconceptsofdependence[J].AnnMathStat, 1966，37：1137-1153.

[2]JOAG-DEV K, PROSCHAN F. Negative association of random variables with applications[J]. Ann-Statist,1983(11):286-295.

[3]NEWMAN C M. Asymptotic independence and limit theorems for positively and negatively dependent random variables[C]//TONG Y L. Inequalities in Statistics and Probability. Hayward:Inst Math Statist，1984(5)：127-140.

[4]王岳宝，严继高,成凤旸,等.关于不同分布两两NQD列的Jamison型加权乘积和的强稳定性[J].数学年刊:A辑,2001,22(6):701-706.

WANG Yuebao, YAN Jigao, CHENG Fengyang, et al. On the strong stability for Jamison type weighted product sums of pairwise NQD series with different distribution[J]. Chinese Annals of Mathematics:SerA,2001,22(6):701-706.

[5]吴群英.两两NQD列的收敛性质[J].数学学报,2002,45(3):617-624.

WU Qunying. Convergence properties of pairwise NQD random sequences[J].Acta Mathematica Sinica, 2002,45(3):617-624.

[6]陈平炎.两两NQD列的强大数定律[J].数学物理学报:A辑,2005,25(3):386-392.

CHEN Pingyan. On the strong law of large numbers for pairwise NQD random variables[J].Acta Mathematica Scientia:SerA,2005,25(3):386-392.

[7]万成高.两两NQD列的大数定律和完全收敛性[J].应用数学学报：中文版,2005,28(2):253-261．

WAN Chenggao. Law of large numbers and complete convergence for pairwise NQD random sequences [J]. Acta Mathematicae Applicatae Sinica:Chinese Series，2005,28(2):253-261．

[8]陈平炎.两两NQD随机序列的Lr收敛性[J].数学物理学报：A辑,2008,28(3):447-453.

CHEN Pingyan.Lrconvergence for pairwise NQD random variables[J]. Acta Mathematica Scientia:SerA, 2008,28(3):447-453.

[9]WU Y F,GUAN M. Mean convergence theorems and weak laws of large numbers for weighted sums of dependent random variables[J]. J Math Anal Appl,201l,377(2):613-623.

[10]邱德华,甘师信.两两NQD列随机变量序列的完全收敛性[J].武汉大学学报:理学版,2013,59(3):285-290.

QIU Dehua, GAN Shixin. Complete convergence for sequences of pairwise NQD random variables[J]. Journal of Wuhan University: Natural Sciences Edition,2013,59(3):285-290.

[11]穆燕,汪忠志.关于两两NQD随机序列的一个极限定理[J].应用概率统计,2014,30(3):289-295.

MU Yan, WANG Zhongzhi. A limit theorem for pairwise NQD random variables[J]. Chinese Journal of Applied Probability and Statistics,2014,30(3):289-295.

Lpconvergence for weighted sums of arrays with pairwise NQD sequences. Journal of Zhejiang University(Science Edition), 2016,43(2):164-167

Abstract:Lp convergence for weighted sums of arrays with pairwise NQD sequences was studied. The corresponding results about CHEN are obtained under the weaker conditions, which extends the well-known theorems in the previous papers.

Key Words:arrays with pairwise NQD sequences; weighted sums; Lp convergence

中图分类号：O 211.4

文献标志码：A

文章编号：1008-9497(2016)02-164-04

DOI：10.3785/j.issn.1008-9497.2016.02.007

基金项目：安徽省高校自然科学研究重点项目(Kj2016A705);安徽省高校优秀青年人才支持计划重点项目(gxyqZD2016317). 宋明珠(1979-)，ORCID:http://orcid.org/0000-0002-4529-6306,女，硕士，讲师，主要从事随机环境中的马氏链研究,E-mail:songmingzhu2006@126.com.

收稿日期：2015-05-18.