折线Mamdnai模糊系统及其权值参数的萤火虫优化算法

索春凤, 王贵君

(天津师范大学 数学科学学院, 天津 300387)



折线Mamdnai模糊系统及其权值参数的萤火虫优化算法

索春凤, 王贵君*

(天津师范大学 数学科学学院, 天津 300387)

摘要：折线Mamdnai模糊系统是基于折线模糊数的线性运算构造的系统模型,其主要特点是前件模糊集及后件中心连接权均取值于由有限个有序点决定的折线模糊数. 依据折线模糊规则建立了折线Mamdnai模糊系统模型,进而基于适应度函数、荧光素和决策半径设计了该系统权值参数的萤火虫优化算法,以优化该系统的后件中心连接权参数.最后,通过一个双输入单输出仿真实例，验证了该萤火虫优化算法的有效性.

关键词：折线模糊数;折线Mamdnai模糊系统;后件中心连接权;萤火虫优化算法

SUO Chunfeng, WANG Guijun

(SchoolofMathematicsSciences,TianjinNormalUniversity,Tianjin300387,China)

2009年,剑桥大学YANG教授受自然界萤火虫发光的生物学启发，首次提出了仿生算法.此算法的主要特点是通过搜索空间中的粒子寻找最优解,并在连续和离散空间优化权值参数,该算法曾被广泛应用于诸多研究领域[1-3].在此基础上兴起了群智能优化仿生算法，包括粒子群算法、遗传算法、蚁族算法等[4-6].2002年,刘普寅教授[7]首次提出折线模糊数概念及其算术运算,该运算不仅满足线性和封闭性,而且克服了基于Zadeh扩展原理的传统模糊数运算的复杂性.此外,文献[7]还率先引入单输入单输出(SISO)折线模糊神经网络(PFNN),并证明了该网络比传统BP模糊神经网络具有更强的逼近性.文献[8]通过引入K-积分模研究了该网络对一类可积函数的逼近性能.文献[9-10]基于Armijo-Goldstein线性搜索准则设计了折线FNN的共轭梯度算法和GA-BP混合算法,从而改进了权值参数的全局寻优能力.文献[11]则讨论了训练模式对的摄动对该网络稳定性的影响.然而,上述学习算法和逼近性能都是针对SISO折线FNN所获得.文献[12]首次提出多输入单输出(MISO)折线FNN结构模型,并依据折线模糊数的线性运算设计了该网络的Hebb算法和粒子算法,具有一定的随机性和参数多样性,Hebb算法直观且易实现,而粒子算法稳定性好且收敛速度较快.然而,传统模糊系统依据前件和后件模糊规则来构造数学模型,其拓扑结构图类似于一个模糊神经网络(FNN).

近年来,利用模糊系统获得模糊规则颇受人们青睐,有研究对T-S模糊系统实施网络分层方法,并采用离散二进制微粒位置表示该模型的结构参数,这不仅减少了规则数,也降低了优化权值参数的复杂性.本文主要依据折线模糊数及其线性运算首次提出折线Mamdnai模糊系统,并通过改进萤火虫算法、适应度函数、荧光素和决策半径，对折线Mamdnai模糊系统的中心连接权参数实施优化,以便提高算法精度和收敛速度.

1预备知识

一般模糊数的算术运算遵循Zadeh扩展原理,但即使最简单的三角形模糊数加减法运算也都颇显复杂,以致这种运算时常不被人们看好.2002年,为了近似地实现模糊数之间的非线性运算，刘普寅教授[7]首次提出n-折线模糊数概念及其算术运算,这种运算不仅具有线性性和封闭性,而且大大降低了传统模糊数运算的复杂性.

本文用Rn表示n维欧式空间,N表示自然数集,R+表示正实数集,F0(R)表示R上所有模糊数构成的集合.下面,综合文献[7-8]给出n-折线模糊数的定义及其相关算术运算.

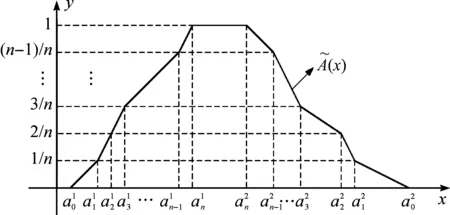
图1　n-折线模糊数的隶属函数图像Fig. 1　Membership function image of

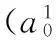
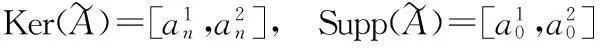
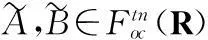
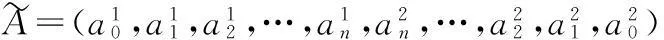
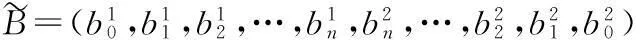
界定n-折线模糊数加减和数乘运算如下:

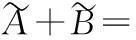
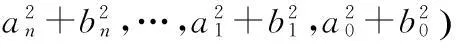
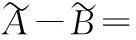
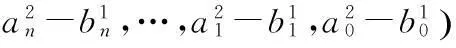
③设k≥0,则

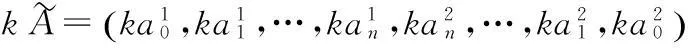
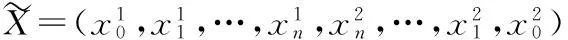
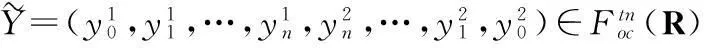
界定度量

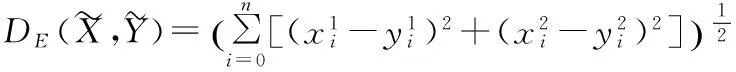
2折线Mamdnai模糊系统

不妨设折线Mamdnai模糊系统由L条模糊规则组成,第k条模糊规则表示为

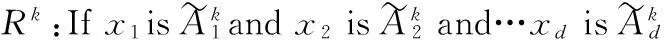
仿照传统模糊神经网络结构图可给出折线Mamdnai模糊系统的拓扑结构图如图2所示.

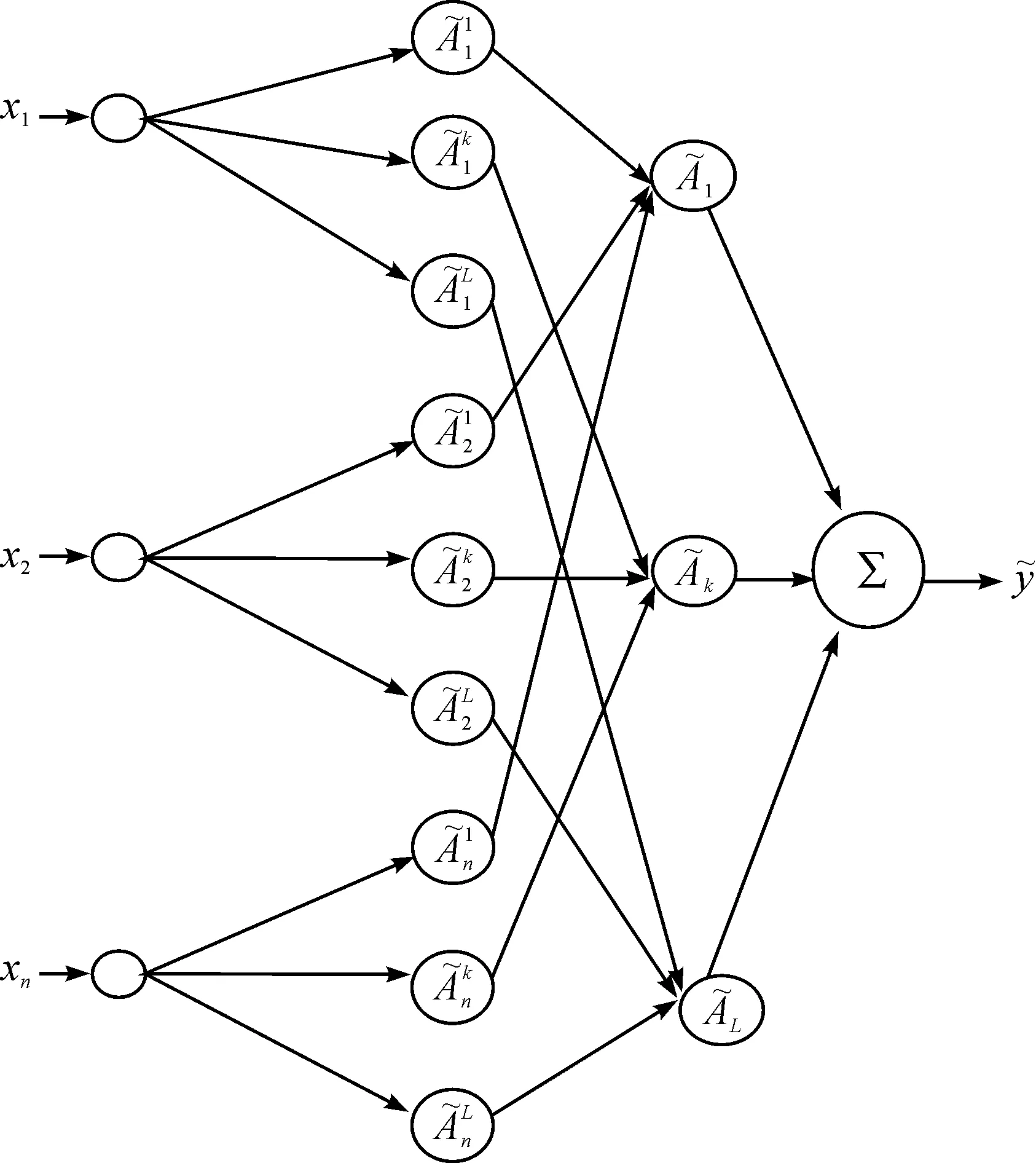
图2　折线Mamdnai模糊系统的拓扑结构Fig. 2　Topological structure of polygonalMamadnai fuzzy system

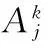
(1)

(2)

其中,输入变量x=(x1,x2…,xd)∈(R+)d,且

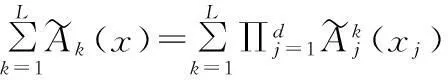
则对每个k=1,2,…,L均满足

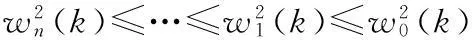
j=1,2;i=0,1,2,…,n.

注1由于n-折线模糊数是由2n+2个有序点确定的,因此可把折线Mamdnai模糊系统的输出看成是清晰输出.但对于传统模糊神经网络来说,其初始权值和阈值一般均是模糊数,当然其输出也是模糊数.由于基于Zadeh扩展原理的模糊数算术运算极其复杂,通常计算系统的输出(模糊数)更是难上加难.文献[9-12]曾基于折线模糊数的运算讨论了3层前向折线模糊神经网络及其学习算法,从而使该网络运算简单了许多.但是优化网络时需优化的参数较多,致使优化速度变慢.本文将传统Mamdnai模糊系统看作一个3层前向折线模糊神经网络.目前仅讨论输出中心连接权为折线模糊数,故需优化的参数大幅度减少!但对于文献[9-10]所提到的BP算法和共轭梯度算法来说,折线Mamdnai模糊系统的权值参数优化算法是否加快了收敛速度或避免了陷入局部极小点仍没有定论.因此,本文基于文献[3-4]提出了改进萤火虫算法,该算法具有较好的鲁棒性和直观性等特点.

3萤火虫算法设计

萤火虫在群聚过程中通过自身散发的荧光素进行交流、觅食及寻偶繁殖.通常情况萤火虫散发的荧光素越亮越吸引萤火虫聚集在它周围.萤火虫算法是基于萤火虫通过荧光素交流思想而提出的一种仿生群智能算法.本节将从萤火虫聚集的荧光素和决策半径入手设计算法.

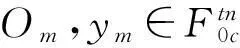
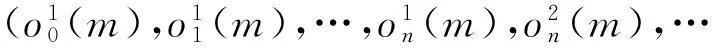
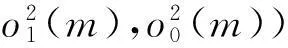
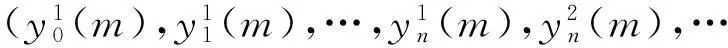
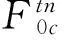
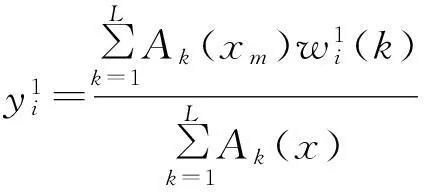
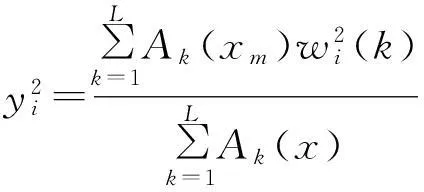
根据n-折线模糊数的度量DE定义折线Mamdnai模糊系统的适应度函数

E.

(3)

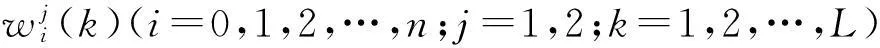
W=(w1,w2,…,wk,…,wL),

其中,每个分量wk为

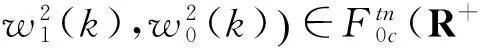
不妨将多维向量W=(w1,w2,…,wk,…,wL)视为方程(3)的一个可行解,此时,每个萤火虫都依适应度函数E(W)决定一个值.现随机给定一组初始解(萤火虫初始位置)WP(p为解个数)，并限定每个萤火虫的荧光素及决策半径.由于萤火虫根据荧光素的亮暗程度和自身感知范围来决定自身的移动方向和距离,故在迭代中通过选择向比自己亮的邻近萤火虫方向移动,当然决策半径也会随之改变,进而通过计算适应度函数E(W)来考证此时位置是否就是萤火虫的最佳位置;如不是,则进行循环迭代,直至找到最优个体极值位置,当然此时位置也是全局极值.

此外,萤火虫算法由于受其移动的距离影响会导致自身收敛速度变慢和精确度降低,为此参考文献[6]改变移动策略来研究折线Mamdnai模糊系统中后件中心连接权值的优化问题.

依文献[3]给出的萤火虫向荧光素亮的邻近萤火虫移动后荧光素的计算公式：

lp(t+1)=(1-ρ)lp(t)+γE(Vp(t+1)).

(4)

其中,lp(t)表示第p个萤火虫在t次迭代过程中的荧光素,lp(t+1)表示第p个萤火虫在t+1次迭代中的荧光素,E(Wp(t+1))是依据式(3)复合得到的适应度函数值,γ是荧光素的更新率,常数ρ满足0<ρ<1.

设第t次迭代过程中第i个萤火虫向第j个萤火虫移动的概率为pij(t)，其计算公式为

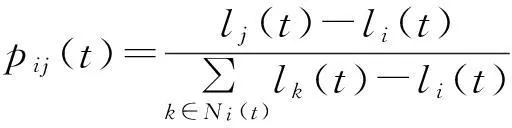
(5)

在决策半径内荧光素高的萤火虫个数为:

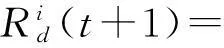
β(nt-|Nt(t)|)}}，

(6)

其中,Rs为感知半径,β为控制参数,nt为虫周围邻近数目.

另外,由于折线Mamdnai模糊系统的后件中心连接权由2n+2个有序参数确定,不妨将其设为萤火虫算法中每个个体的编码长度.因此,通过计算适应度函数值、更新位置、决策半径和荧光素找到最佳函数值对应的个体,从而优化萤火虫群体.

下面针对折线Mamdnai模糊系统的权值参数给出萤火虫优化算法的步骤如下:

Step 1初始化.给定自然数n0作为迭代过程中每一阶段萤火虫的总数,并随机选取n0个初始位置的参数向量Wp=Wp[0]=(w1,w2,…,wk,…,wL)和初始荧光素Lp(0)=(l1p,l2p,…,lLp),p=1,2,…,n0.给定精度ε>0,初始迭代步骤t=0,最大迭代步骤是T.

Step 2计算实际输出和适应度值.依据定义2将随机选取的初始后件中心连接权值WP[0]代入式(2)计算实际输出值,再根据式(3)计算适应度函数值E(Wp[0]).

Step 3更新荧光素值.如果发现某个萤火虫邻近的萤火虫荧光素比自己更亮,则要根据式(4)设置常数ρ和γ,并重新计算自身的荧光素值.

Step 4更新萤火虫位置.当第i个萤火虫找到第j个萤火虫时,且两者之间的距离小于决策半径,则萤火虫i将按式(5)的概率向萤火虫j移动,具体计算公式如下:

其中,lbp[t]是萤火虫自身达到的最佳位置,而abp[t]是群体达到的最佳位置,Wp[t+1]表示产生的新位置,i,j,p∈{1,2,…,n0},i≠j≠p,且rp∈[-1,1],φ∈[0,1].

Step 5更新决策半径.当萤火虫向荧光素亮的萤火虫移动时会使自身亮度增强,从而使决策半径发生变化.此时,可依式(6)设置感知半径Rs和参数β,以便随时更新决策半径.

Step 6判断输出后件中心权值参数向量Wp(t+1)中每2n+2个参数是否满足由小到大次序,若满足则直接转Step 6;否则,将这2n+2个参数由小到大重新排序后再转Step 6.

Step 7若迭代超过最大步次数T或达到设定精度ε,则退出操作;否则,返回执行Step 2.

Step 8输出萤火虫的最佳位置参数Wp.

注2Step 4中移动方案采用了人工蜂群算法[6],但由于本文针对n-折线模糊中2n+2个正有序实数进行优化,故其优化步骤要有别于常规神经网络的优化算法.为此,将被优化的参数组成一个多维向量,考虑这2n+2个正实数的有序性,因此算法Step 6中须将次序调整为由小到大排列.

4模拟实例

本节将通过一个双输入单输出折线Mamdnai模糊系统例子来验证优化权值参数的有效性.

设荧光虫的初始荧光素为

Lp(0)=(l1p,l2p,…,lsp),

其中,lip∈[0,5].现给定计算荧光素和决策半径的实参数分别为:ρ=0.8,γ=0.05,β=0.65.再设d=2,n=3,给定精度ε=0.001,规则库由L(=2)条规则组成,其中每条规则的形式如下：

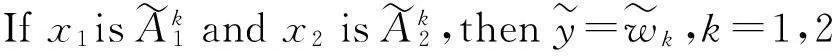
根据式(2)折线Mamdnai模糊系统的实际输出表达为

(7)

其中,∀x=(x1，x2)∈(R+)2.

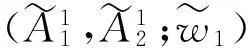
3-折线模糊数A11(0.00,0.21,1.17,1.22,1.70,1.85,3.30,3.58)A12(1.98,2.20,2.95,3.25,4.20,5.50,5.95,6.10)w1(0.11,0.13,0.17,0.22,0.30,0.35,1.30,1.88)

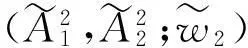
3-折线模糊数A21(0.00,0.31,1.34,1.42,1.70,2.85,3.30,3.85)A22(1.48,1.55,2.85,3.25,3.55,3.78,4.05,5.15)w2(0.38,0.40,1.25,1.85,2.20,2.50,2.65,3.10)

依据表1与2的数据给出2个训练模式对的3-折线模糊数的隶属函数图像如图3～5所示.按萤火虫优化算法可获得优化的后件中心连接权、系统实际输出和期望输出的图像如图6～8所示.

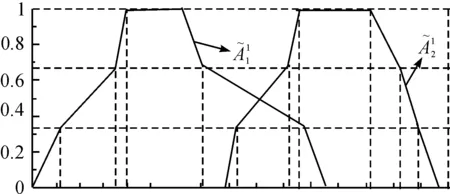
图3　前件和的隶属函数图像Fig. 3　The membership function of

图4　前件和的隶属函数图像Fig. 4　The membership function of

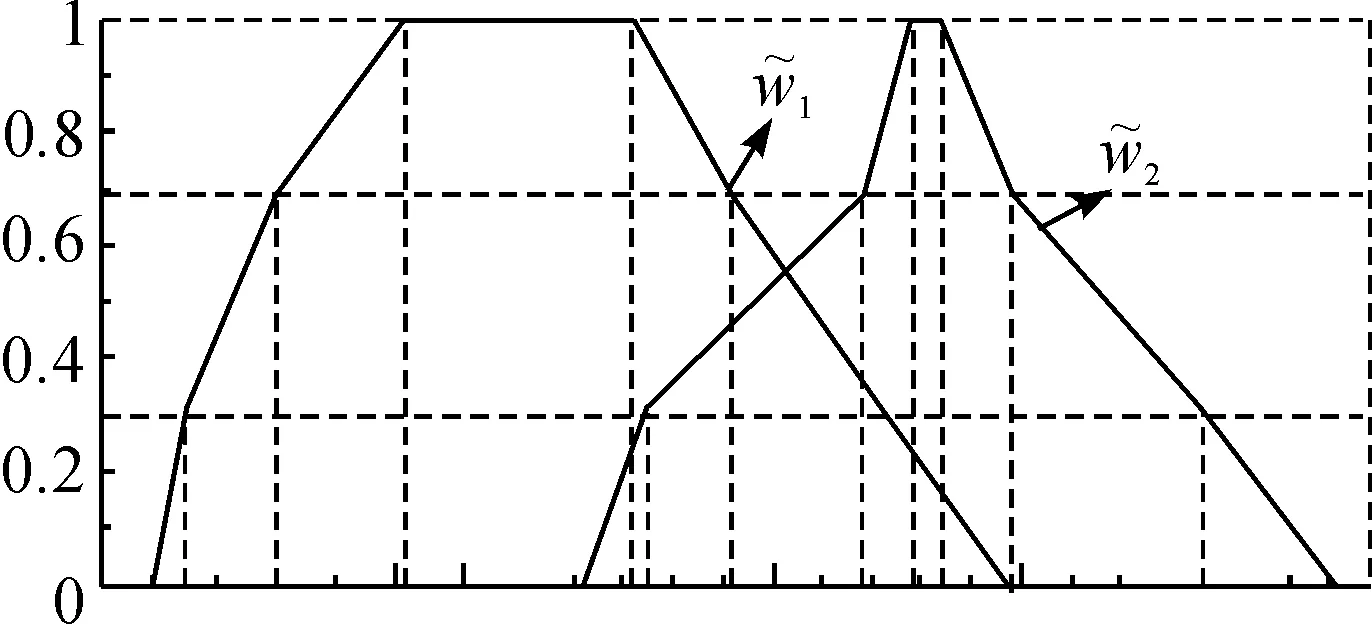
图5　后件中心连接权1和2的图像Fig. 5　Centre connection weights 2

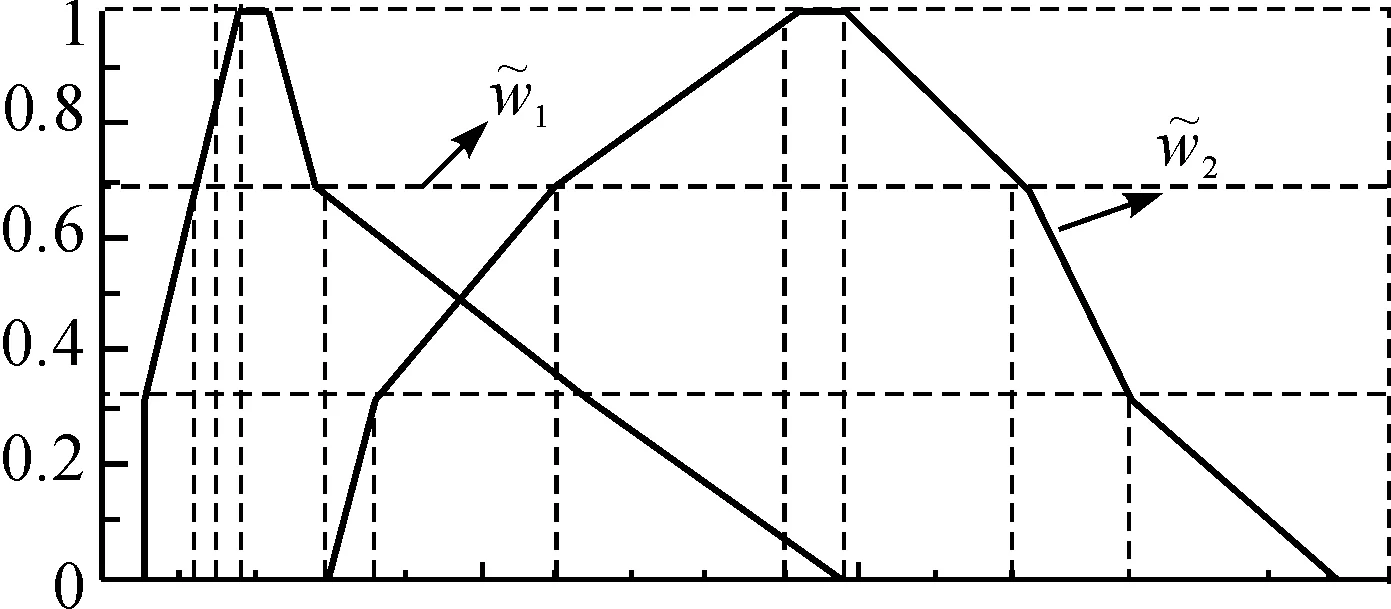
图6　优化的后件中心连接权图像Fig. 6　Connection weights of consequent centre

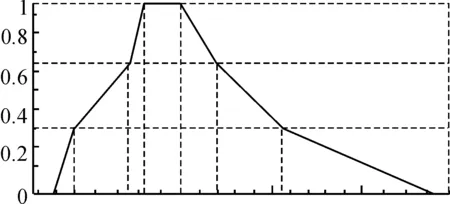
图7　系统的实际输出图像Fig. 7　The actual output of the

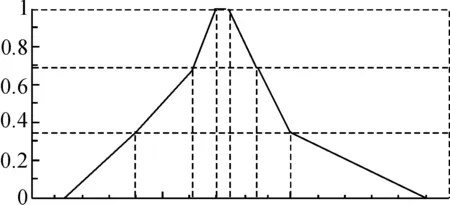
图8　系统的期望输出图像Fig. 8　The expected output of the

再将后件中心连接权组成一个多维向量,按照萤火虫优化算法1～8步及题设参数，优化的后件中心连接权值参数、系统实际输出和期望输出的数据值如表3与4.

表3　优化后系统的后件中心连接权值

表4　折线Mamdnai模糊系统实际和期望输出

在上述系统的优化过程中,涉及计算的次数比较多,因此可以利用MATLAB软件计算获得萤火虫优化算法的迭代次数与误差变化的误差迭代图(见图9).

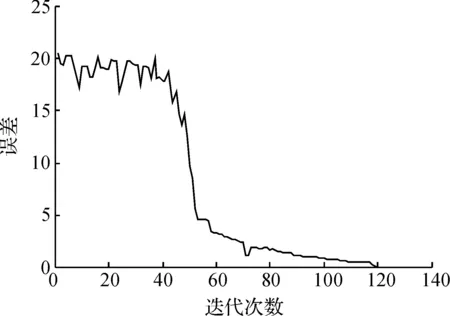
图9　总误查变化迭代图Fig. 9　The change of the total error

从图9不难看出，萤火虫优化算法大约50步前误差相对偏高,之后大幅降低,直至迭代120步时误差趋于平稳,从而达到所给精度.

5结论

基于后件中心连接权取值为n-折线模糊数引入了折线Mamdnai模糊系统,设计了萤火虫算法来优化该系统的后件中心连接权.由仿真实例不难看出，该萤火虫优化算法在迭代次数不是很高的情况下就能达到低精度.但由于折线Mamdnai模糊系统主要依赖于n-折线模糊数的运算,涉及的参数较多,而且随着该系统调节参数的不断增多，可能会使计算机记忆溢出或出现延迟现象.因此,如何克服该算法的这些缺陷需进一步探索.

参考文献(References)：

[1]周永权,黄正新,刘洪霞.求解TSP问题的离散型萤火虫群优化算法[J].电子学报,2012,40(6):1164-1170.

ZHOU Yongquan, HUANG Zhengxin, LIU Hongxia. Discrete glowworm swarm optimization algorithm for TSP problem[J]. Acta Electronica Sinica,2012, 40(6):1164-1170 .

[2]李永梅,周永权,韦军.用于函数优化的层次结构萤火虫群算法[J].应用科学学报,2012,30(4):391-396.

LI Yongmei, ZHOU Yongquan, WEI Jun. Using hierarchical structure glowworm swarm algorithm for function optimization[J]. Journal of Applied Sciences,2012,30(4):391-396.

[3]候越,赵贺,路小娟.基于萤火虫优化的BP神经网络算法研究[J].兰州交通大学学报,2013,32(6):24-27.

HOU Yue, ZHAO He, LU Xiaojuan. Study on glowworm swarm optimized BP neural network algorithm [J]. Journal of Lanzhou Jiaotong University,2013,32(6):24-27.

[4]刘长平,叶春明.一种新颖的仿生群智能优化算法:萤火虫算法[J].计算机应用研究,2011,28(9):3295-3297.

LIU Changping, YE Chunming. Novel bioinspired swarm intelligence optimization algorithm: Firefly algorithm[J]. Application Research of Computers,2011,28(9):3295-3297.

[5]吴斌,崔志勇,倪卫红.具有混合群智能行为的萤火虫群优化算法研究[J].计算机科学,2012,39(5):198-200.

WU Bing, CUI Zhiyong, NI Weihong. Research on glowworm swarm optimization with hybrid swarm intelligence behavior [J]. Computer Science,2012,39(5):198-200.

[6]喻金平,郑洁,梅洪标.基于改进人工蜂群算法的K均值聚类算法[J].计算机与应用,2014,34(4):1065-1069.

YU Jinping, ZHENG Jie, MEI Hongbiao. K-means clustering algorithm based on improved artificial bee colony algorithm[J]. Journal of Computer Applicati-ons,2014,34(4):1065-1069.

[7]刘普寅.一种新的模糊神经网络及其逼近性[J].中国科学：E辑,2002,32(1):76-86.

LIU Puyin. A new fuzzy neural network and its approximation capability [J]. Science in China：Ser E, 2002,32(1):76-86.

[8]王贵君,李晓萍.K-积分模意义下折线模糊神经网络的泛逼近性[J].中国科学：信息科学,2012,42(3):362-378.

WANG Guijun, LI Xiaoping. Universal approxima-tion of polygonal fuzzy neural networks in sense of K-integral norms [J]. Scientia Sinica Informationis,2012,42(3):362-378.

[9]何英,王贵君.折线模糊神经网络的共轭梯度法[J].电子学报,2012,40(10):2079-2084.

HE Ying, WANG Guijun. Conjugate gradient algori-thm of the polygonal fuzzy neural networks [J]. Acta Electronica Sinica,2012,40(10):2079-2084.

[10]YANG Yongqiang, WANG Guijun, YANG Yang. Parameters optimization of polygonal fuzzy neural networks based on GA-BP hybrid algorithm [J].International Journal of Machine Learning and Cybernetics,2014,5(5):815-822.

[11]隋晓琳,王贵君.训练模式对摄动对折线模糊神经网络稳定性的影响[J].模式识别与人工智能,2012,26(6):928-936

SUI Xiaolin, WANG Guijun. Influence of perturba-tion of training pattern pairs on stability of polygonal fuzzy neural networks[J]. Pattern Recognition and Artificial Intelligence,2012,26(6):928-936.

[12]王贵君,何英,李晓萍.基于MISO折线模糊神经网络的优化算法[J].中国科学：信息科学,2015,45(5):650-667.

WANG Guijun,HE Ying,LI Xiaoping. Optimization algorithm for MISO polygonal fuzzy neural network[J].Scientia Sinica Informationis，2015,45(5):650-667.

Polygonal Mamdnai fuzzy system and the firefly optimization algorithm of its weight parameters. Journal of Zhejiang University(Science Edition), 2016,43(2):149-155

Abstract:The polygonal Mamadnai fuzzy system is a model based on the linear operation of polygonal fuzzy numbers, and its main characteristic is that the antecedent fuzzy sets and consequent centre connection weights are decided by finite points of a polygonal fuzzy number. In this paper, a polygonal Mamdnai fuzzy system is constructed by some polygonal fuzzy rules, and a firefly optimization algorithm for the weigh parameters is designed based on the fitness function, fluorescein and decision radius. Therefore, the consequent centre connection weights of this system are optimized. Finally, through a double input and single output simulation instance, we verify the effectiveness of the firefly optimization algorithm.

Key Words:polygonal fuzzy numbers; polygonal Mamadnai fuzzy system; consequent centre connection weights; firefly optimization algorithm

中图分类号：TP 183;O 159

文献标志码：A

文章编号：1008-9497(2016)02-149-07

DOI:10.3785/j.issn.1008-9497.2016.02.005

作者简介：索春凤(1990-),ORCID:http://orcid.org/000-0001-7082-8151,女,硕士研究生,主要从事模糊神经网络与模糊系统研究，E-mail:1242362420@qq.com.*通信作者， E-mail:tjwgj@126.com.

基金项目：国家自然科学基金资助项目(61374009).

收稿日期：2015-06-08.