一个与Euler数有关的Hilbert型不等式的推广

有 名 辉

(浙江机电职业技术学院 数学教研室， 浙江 杭州 310053)



一个与Euler数有关的Hilbert型不等式的推广

有 名 辉

(浙江机电职业技术学院 数学教研室， 浙江 杭州 310053)

摘要：通过引入参数，利用实分析技巧，建立最佳常数因子与余割函数有关的Hilbert型积分不等式，推广了与Euler数有关的Hilbert型不等式. 作为结论的应用，赋予参数不同的值，给出了一些特殊结果．

关键词：Hilbert型积分不等式；余割函数；Euler数; 部分分式展开; Gamma函数

YOU Minghui

(MathematicsTeachingandResearchSection,ZhejiangInstituteofMechanicalandElectricalEngineering,Hangzhou310053,China)

设f(x),g(x)≥0,且

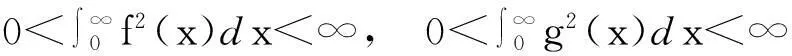
则

(1)

其中π2是满足式(1)的最佳常数因子[1].不等式(1)通常被称为Hilbert型不等式,在分析学及其应用领域有着重要的作用[2].近年来，通过引进参数，研究者们给出了式(1)及其对应级数形式的一些推广和改进，取得了一系列有价值的成果[3-13].

最近，周昱等[14]证明了一个类似于式(1)并与Euler数有关的不等式，即

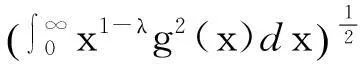
(2)

其中λ>0,E0=1,En(n∈N+)是Euler数，即E1=1,E2=5,E3=61,E4=1385，….

作为式(2)的推广，本文将建立一个常数因子与余割函数有关的Hilbert型不等式.

1定义及引理

定义1[15]对于a>0，定义

为第2型欧拉积分，即Γ函数.特别地，当a∈Z+时，Γ(a)=(a-1)！.

引理1设λ,α,β>0,且α+β=λ,n为非负整数，φ(x)=cscx,则

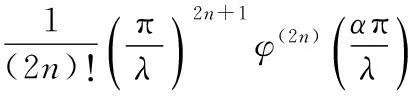
证明由φ(x)=cscx的部分分式展开形式(见文献[15],P397)：

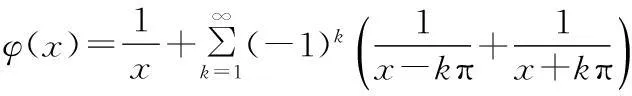
(3)

式(3)两边关于x求2n阶导数，得

φ(2n)(x)=(2n)！·

(4)

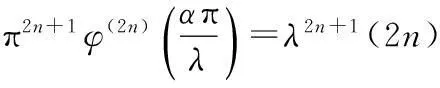
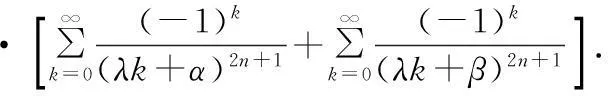
由此，证得引理1成立.

引理2n为非负整数,E0=1,En(n∈N+)是Euler数,φ(x)=cscx,则

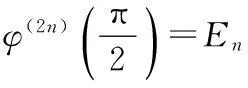
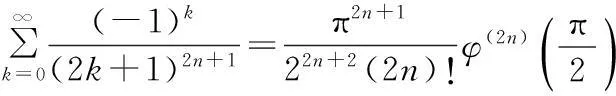
(5)

而由文献[16]，可知

(6)

由式(5)和(6),可知引理2成立.

引理3设λ,α,β>0,且α+β=λ,n为非负整数,φ(x)=cscx,则

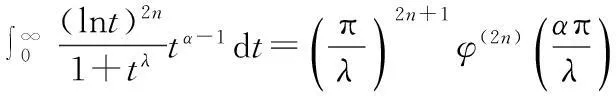
证明当t∈[0,1)时，

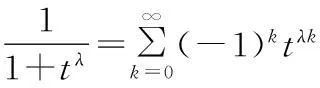
故

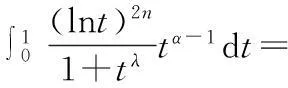
因此,

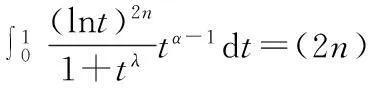
(7)

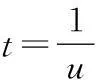
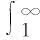
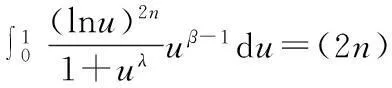
(8)

结合式(7)和(8)，并利用引理1,可得引理3.类似地，有

引理4设λ,α,β>0,且α+β=λ,n为非负整数,φ(x)=cscx,则

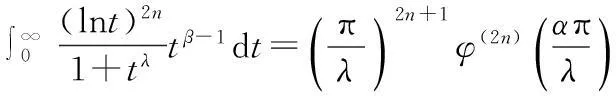
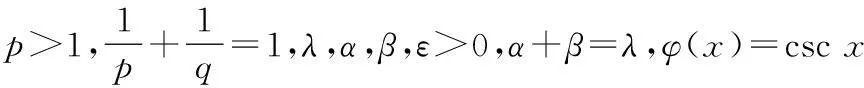
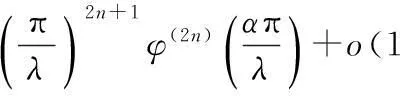
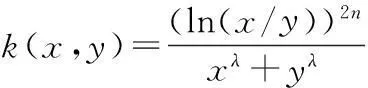
(9)

令ε→0+，由引理4，可得

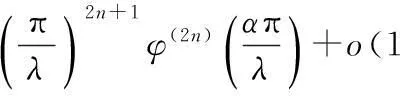
(10)

由式(9)和(10)，即得引理5.

2定理

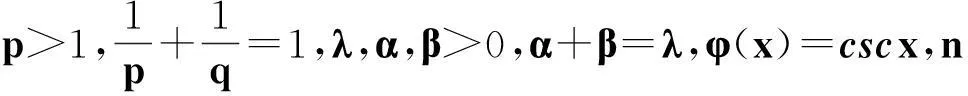
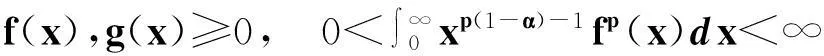
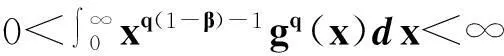
则

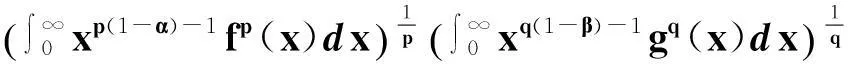
(11)

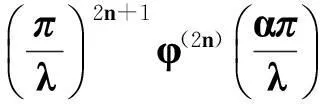
证明由Hölder不等式，可知

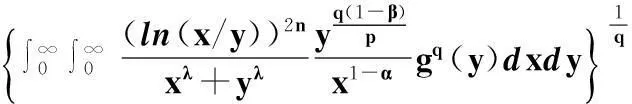
(12)

若式(12)取等号，则有不全为0的实数A与B,使得

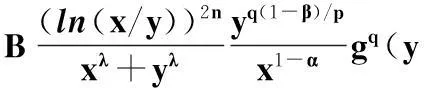
a.e.于(0,∞)×(0,∞)(参见文献[17])，即

Axp(1-α)fp(x)=Byq(1-β)gq(y).

a.e.于(0,∞)×(0,∞).于是，有常数C，使得

Axp(1-α)fp(x)=C,a.e.于(0,∞)；

Byq(1-β)gq(y)=C,a.e.于(0,∞).

通过变量替换，结合α+β=λ,根据引理4,不难算得

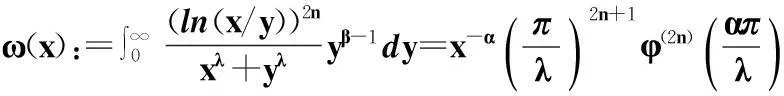
类似地，根据引理3,又可算得

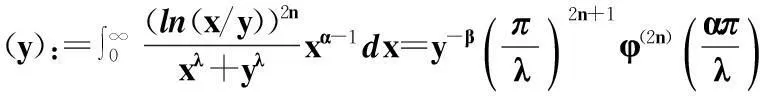
因此，式(12)可写成

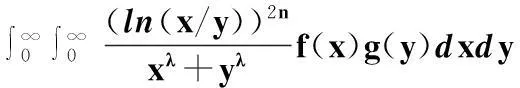
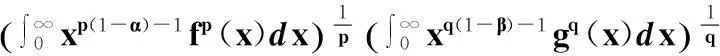
事实上，若此常数因子非最佳，则存在实数

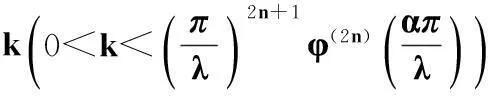
使得式(11)中的常数因子换成k后式(11)仍成立．即

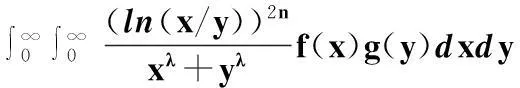
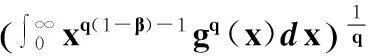
(13)

定义函数fε(x)和gε(x)(其中ε充分小)如下：

若x∈(0,1)，令

fε(x)=gε(x)=0；

若x∈[1,∞)，令

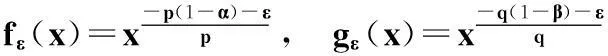
用fε和gε分别取代式(13)中的f和g，则

将引理5的结果代入，可得

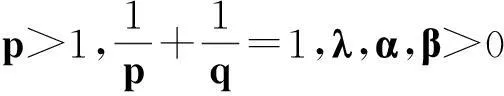
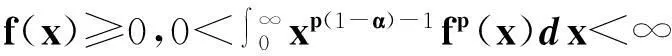
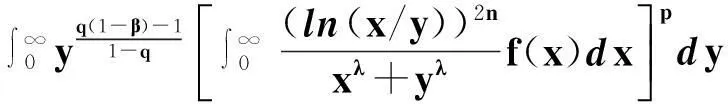
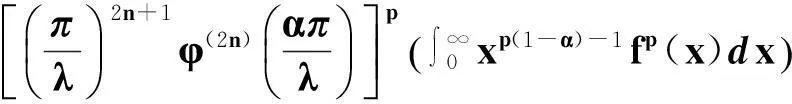
(14)

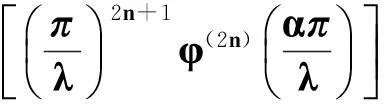
证明令

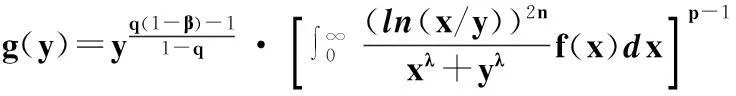
则由式(11)可得

(15)

故

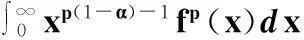
(16)

结合定理2的条件和式(16),可知应用定理1的条件是充分的.因此式(15)和(16)都取严格不等号.故式(14)成立.

以上由式(11)证得了式(14).要说明式(11)和式(14)等价，只需从式(14)证得式(11).事实上，由Hölder不等式，可知

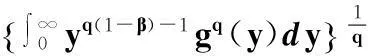
(17)

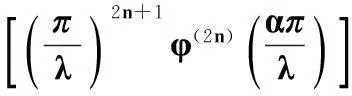
3推论

赋予定理1中的参数不同的值，可以得到一些特殊的结果.

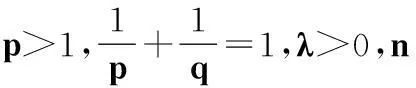
且

则

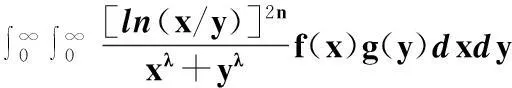
(18)

注1在式(18)中,令p=q=2，即得式(2),因此定理1是式(2)的推广.另外，若在式(18)中,令λ=2，则有

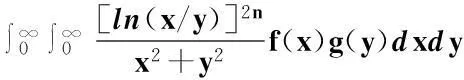
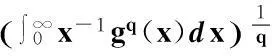
(19)

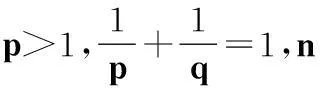
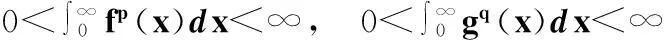
则

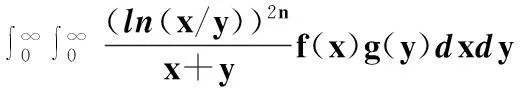
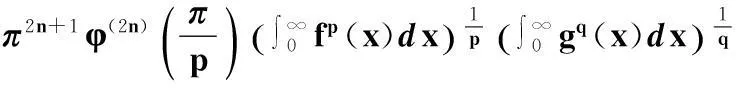
(20)

在定理1中，令λ=1,n=0，则有

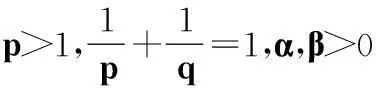
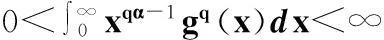
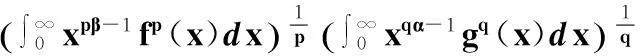
(21)

参考文献(References)：

[1]HARDY G H, LITTLEWOOD J E, POLYA G .Inequalities[M]. London：Cambridge University Press,1952.

[2]MINTRINOVIC D S, PECARIC J E, FINK M． Inequalities Involving Functions and Their Integrals and Derivatives[M]. Boston: Kluwer Academic Press,1991.

[3]杨必成．关于一个Hilbert类积分不等式的推广及应用[J]．应用数学，2003,16(2)：82-86．

YANG Bicheng．On a generalization of a Hilbert’s type integral inequality and its application[J]. Mathematics Applicata，2003,16(2):82-86．

[4]杨必成．一个推广的Hilbert型积分不等式及其应用[J]. 数学杂志，2007,27(3)：285-290.

YANG Bicheng．An extension of the Hilbert’s type integral inequality and its application[J]. Journal of Mathematics，2007, 27(3):285-290．

[5]付向红，和炳.具有两个参数的Hilbert型积分不等式[J].吉林大学学报：理学版，2010,48(4)：595-599.

FU Xianghong, HE Bing. Hilbert-Type integral inequality with two parameters[J]. Journal of Jilin University: Science Edition,2010,48(4):595-599.

[6]KUANG J, DEBNATH L. On new generalizations of Hilbert’s inequality and their applications[J]. J Math Anal Appl, 2000, 245(1)：248-265．

[7]杨必成．关于一个推广的具有最佳常数因子的Hilbert类不等式及其应用[J].数学研究与评论，2005,25(2)：341-346.

YANG Bicheng. Generalization of a Hilbert-Type integral inequality with the best constant factor and its applications[J]．J Math Res Exposition,2005,25(2)：341-346．

[8]杨必成．一个推广的具有最佳常数因子的Hilbert型不等式[J].吉林大学学报：理学版，2006,44(3)：333-337.

YANG Bicheng. A generalized Hilbert-Type inequality with a best constant factor[J]. Journal of Jilin University: Science Edition，2006, 44(3):333-337.

[9]杨必成．一个较为精密的Hardy-Hilbert型不等式及其应用[J].数学学报：中文版，2006,49(2)：363-368.

YANG Bicheng. On a more accurate Hardy-Hilbert’s type inequality and its application[J]． Acta Math Sinica: Chinese Series,2006,49(2)：363-368.

[10]JIN Jianjun．A new generalization of Hardy-Hilbert type inequality with multi-parameters[J]． J Math Res Exposition,2009,29(6)：1131-1136．

[11]孙保炬．一个推广的Hardy-Hilbert型不等式[J].科技通报，2012,28(5)：18-23.

SUN Baoju. A more accurate Hilbert type inequality[J]. Bulletin of Sci and Tech，2012,28(5):18-23.

[12]JIN Jianjun. On Hilbert’s type inequalities[J].J Math Anal Appl,2008,340(2):932-942.

[13]杨必成.关于一个基本的Hilbert型积分不等式及推广[J]. 大学数学, 2008,24(1)：87-92.

YANG Bicheng. On a basic Hilbert-Type integral inequality and extensions[J]. College Mathematics，2008,24(1): 87-92.

[14]周昱，高明哲.一个新的带参数的Hilbert型积分不等式[J]，数学杂志，2011,31(3)：575-581.

ZHOU Yu, GAO Mingzhe．A new Hilbert type integral inequality with one parameter[J]. Journal of Mathematics，2011,31(3)：575-581.

[15]菲赫金哥尔茨Γ M.微积分学教程:第2卷[M]. 北京：高等教育出版社，2006：397，695.

FAYE HAYZN COYLEF Γ M. Calculus Course :Vol.2[M]．Beijing：Higher Education Press,2006：397，695.

[16]王连祥,方德植.数学手册[M]. 北京：人民教育出版社，1979：16.

WANG Lianxiang, FANG Dezhi. Mathematics Handbook[M].Beijing: People’s Education Press,1979：16.

[17]匡继昌.常用不等式[M].第3版,济南：山东科学技术出版社，2010：5.

KUANG Jichang． Applied Inequalities [M]．3nd ed, Ji’nan：Shandong Science and Technology Press,2010：5.

Generalization of a Hilbert-type inequality related to Euler number. Journal of Zhejiang University(Science Edition), 2016,43(2):144-148

Abstract:By introducing parameters and using the method of real analysis, we establish a Hilbert-type integral inequality with the best possible constant factor which is related to cosecant function. We also prove that the obtained inequality is a generalization of Hilbert-type inequality related to Euler number. Furthermore, as applications of the conclusion, some new and special results are presented by giving the parameters different values．

Key Words:Hilbert-type integral inequality；cosecant function；Euler number；partial fraction expansion；Gamma function

中图分类号：O 178

文献标志码：A

文章编号：1008-9497(2016)02-144-05

DOI:10.3785/j.issn.1008-9497.2016.02.004

作者简介：有名辉(1982-)，ORCID:http://orcid.org/0000-0002-1993-9558,男，讲师，硕士，主要从事解析不等式研究，E-mail:youminghui@hotmail.com.

收稿日期：2015-04-03.