基于改进Wagner方法的轴对称体入水“后时段”砰击载荷数值计算
2016-05-04赵九龙闫发锁
赵九龙,闫发锁,樊 磊
(1.哈尔滨工程大学,哈尔滨150001;2.交通运输部 上海打捞局,上海 200090;3.德州农工大学,德克萨斯州 77840,美国)
基于改进Wagner方法的轴对称体入水“后时段”砰击载荷数值计算
赵九龙1,2,闫发锁1,樊 磊3
(1.哈尔滨工程大学,哈尔滨150001;2.交通运输部 上海打捞局,上海 200090;3.德州农工大学,德克萨斯州 77840,美国)
文章基于三维边界元方法研究了三维轴对称体入水砰击载荷的数值算法。算法从三维力学模型出发,继承Wagner自由液面抬升理论,引入浸深因子Cw以确定自由液面抬升高度,将自由液面线性化处理,同时考虑网格运动,在自由液面附近对网格进行截断重构,以确保水下湿面积的精准。算法中使用考虑加权运动项的非线性伯努利方程计算得到入水结构的表面压力,进一步积分可得入水结构的总体受力;另外,算法中引入虚拟面元的概念,将砰击载荷计算时历延长至液面高于坠物制高点之后,扩大了传统入水载荷计算的时历范围,并且文中引用Alaoui半球入水试验,对算法的正确性及适用性进行了验证。
轴对称体;砰击载荷;液面升高;网格截断;虚拟面元
0 引 言
结构物在短时间内迅速进入液体,随之产生液体飞溅的现象称之为砰击。然而,砰击涵盖的面非常广泛,广义的砰击概念是指结构物与流体发生的碰撞现象,一般都涉及到固、液、气三种介质的相互耦合,是一种瞬态的强非线性、强耦合和极其复杂的物理现象。在工程实际中,砰击问题非常易见,例如:水上飞机水面降落、船舶在恶劣海况中的底部砰击、舰船上的救生艇落水、航天运载器的水面回收、鱼雷空投入水等问题都属于该范畴。
砰击现象对应的的实际力学模型要涉及到固、液、气三种介质的耦合,而且具体情况复杂多变,目前为止仍未能提出一种贴切真实情况、普适性强的理论模型。但是为了便于对问题展开研究,通常使用“结构物入水冲击”模型作为具体的力学模型来分析。
许多工程结构物在高速入水时,所面临的挑战是入水过程瞬时所受到的巨大水动压力,这往往会导致入水结构的局部大变形甚至破断。近年来人们在计算入水压力方面做了许多工作,但是大部分都是以二维视角展开研究,研究基于的入水模型也多见于二维楔形体,数值方面做得比较好的有Wu等[1-2]研究出了二维V形楔的迭代求解方法,并且运用二维边界元法,使用柯西积分计算了楔形体入水的相似解,许国冬[3]讨论了V形楔多种入水形式的相似解。但是由于实际工程应用中人们使用的结构形式多样,二维入水算法存在着一定的应用局限性,因此对于三维入水算法的开发有着迫切的需求。
目前还没有非常成熟的三维入水算法供于应用。近年来的Korobkin和Scolan[4-5]从逆推的Wagner问题及线性Wagner问题两方面出发研究了三维入水砰击理论,解决了流场流动、压力分布及流域形状三方面的问题。Faltisen和Chezhian[6]以非轴对称的船体模型入水为研究对象,基于边界元方法、发展的Wagner理论,研究了三维入水砰击的数值方法。
基于此,本文也在三维入水方面进行了研究,主要研究了基于三维边界元方法的砰击理论算法及其在砰击载荷计算中的应用。数值方面的研究从三维力学模型出发,基于三维边界元方法,继承Wagner自由液面抬升理论,引入了“浸深因子”Cw[7]以确定自由液面抬升的高度,在这一高度处建立新的自由液面并称之为“等效自由液面”。算法中考虑到网格运动,对入水过程中每一时间步时刻对应的网格编号、节点坐标等进行追踪计算,由此得出网格与等效自由液面的位置关系,进一步可精确追踪到每一时间步时刻对应的湿网格数据,同时对等效自由液面附近的网格根据实际情况进行截断重生,以确保水下湿面积的精确;通过时间步的循环计算,最终可得到入水结构的表面“压力”和总体“受力”两种载荷时历。另外,提出了虚拟面元的概念,使算法可以应用于坠物浸水之后的砰击时段(液面高于入水物体的最高点,即所谓的入水“后时段”,将传统的砰击载荷计算时历延长。
1 数值算法
1.1 改进Wagner方法在砰击载荷计算中的应用原理
Wagner在Von-Karman[7]线性砰击理论的基础上,提出了自由液面的抬升效应,采用平板拟合法,相对精确了浸湿半宽、附加质量、冲击力及压力分布的求解。在求解过程中所采用的相当平板是对具体物面的近似,而且采用线性伯努利方程对压力分布进行求解,整个过程虽然计算量小,但是计算精度还有待进一步提高。本文在原始Wagner方法的基础上进行了改进,引入了边界元方法[8],考虑具体浸水物面,采用非线性伯努利方程对压力进行求解。
谈及流体载荷的计算,近年来出现了多种计算方法,比较常用的有摄动法、有限元法、有限差分法、边界元法。由于边界元方法将空间的问题转化为边界表面的积分问题,将问题减小一维,大大减少了未知量的数目,另一方面它能够处理无穷远处的边界条件,对外部问题有很好的适用性,正是由于这两点才使得边界元方法在流体载荷计算中得以迅速发展。本文所使用的边界元方法适用于求解无界流场中的三维无升力绕流问题,分布奇点法的所有要点都包含在内。速度势可以用分布源和分布偶极来描述,本文算法仅仅涉及到分布源的概念。
控制方程及边界条件如公式(1)、(2):

将湿物面划分为N个面元可以得到离散化的方程组:

式中:aij是j面元对i面元的影响系数:
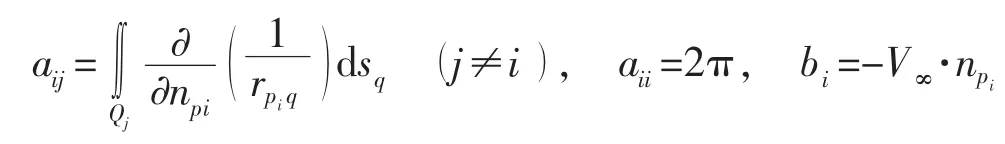
通过求解方程组(3)便可以求解出各面元中心点处的分布源密度,进一步可得到个面元中心点的速度势:

紧接着可以求出各面元中心点处的诱导速度:

再进一步可根据各时刻各点的速度势数值,对时间进行微分计算便可得到这样就可以使用非线性的伯努利方程:

计算得到各时刻对应的绕流压力。
从上面的推导可以计算出无界流中运动物体的表面绕流压力值,但是人们通常研究的入水砰击现象发生在半无界流场中,而且正是自由液面的附近。为了解决理论的适用问题,考虑线性的自由液面,由于自由液面上的速度势φ=0,即可将自由液面下的湿表面沿着自由液面进行上下对称处理,形成一个沿自由液面对称的闭合曲面s+s′,这样就将问题等同于考虑在无界流场中运动的s+s′,使问题适用于上述理论。
1.2 自由液面处理方法
本文算法在对自由液面进行线性化处理的时候,根据Wagner理论,考虑到了液面抬升,如图1所示的入水模型。通常情况下,物体入水过程中,自由液面与物体相交点处的位置均要高于原始的自由液面,流体沿物面有向上爬升的趋势,严格来讲计算过程中必须要追踪自由液面的运动形式,这样一定会使求解更加精确,但是对三维入水模型来讲,自由液面的追踪非常的困难,而且鲜有适用性比较广泛的方法,例如Faltinsen和Chezhian[6],在三维船体入水砰击的自由液面追踪中也不能够很精确地描述自由液面的具体形状及变化,他们所采用的方法是沿着船体与自由液面交界的一圈均匀标记若干点,之后分别以这些标记点为起点,平行于原始的自由液面画出射线,最终由做出的许多射线近似地拟合出一个抬升后的自由液面。该方法目前来讲无疑是一种比较准确的追踪方法,基于此,在自由液面的处理过程中,本文程序也沿用了这种“射线延伸”的近似,但是较之有所简化。
从工程实用角度,为了简化流固交界附近数值处理的难度和计算量。本文算法采用线性化的等效自由液面,使用经验公式换算出物面与自由液面每一时刻的触点高度,以确定该触点位置,并以之为起点平行于水平面引出射线,认为该射线所在的水平面便是新的自由液面,在这里称之为“等效自由液面”。为了确定等效自由液面的位置,同时引入了浸深因子Cw的概念,如图2所示。

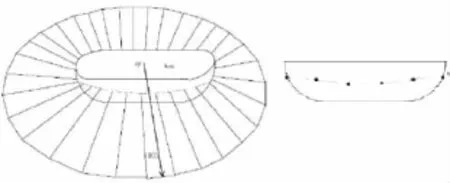
图1 Faltinsen关于自由液面的追踪Fig.1 The free surface tracking method by Faltinsen
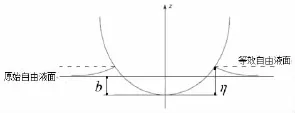
图2 本文采用的自由液面处理方法Fig.2 The free surface caculation by this paper
如果知道Cw值,便很容易可以确定等效自由液面的位置。本文参照了美国水面武器研究中心白橡树实验室的一份研究报告[9],其中详细介绍了轴对称物体垂向入水与任意物体倾斜入水两种类别的Cw值选取办法。

表1 Cw选取方法Tab.1 Calculation of Cw
显然使用该方法可以使砰击载荷计算得到很大程度上简化,提高了计算效率。
1.3 面元网格的运动及重构
本文将边界元模型入水运动的过程划分为若干时间步进行分析,对于每一时间步时刻都要统计出等效自由液面以下的面元及其节点信息,这是计算诱导速度系数的基本前提。很显然,水面以下远离等效自由液面的网格保持原有的完整性,因此不必对其几何形状进行改变;而在等效自由液面附近,沿着物体与自由液面的交界线有一圈网格被等效自由液面截断,生成新的四边形、五边形和三角形面元;但是考虑到本文算法中要求提供的面元必须是长宽比比值适中的四边形面元,而且为了提高程序的精确性,不能单纯地将这部分网格进行忽略,因此在程序中对这部分网格进行了截断重生处理,具体的处理方法如下图3所示。
另外,考虑到网格运动,于是便不能直接使用常规的非线性伯努利方程来计算载荷,需要对其进行改进,添加运动项目。根据泰勒公式变换得到:


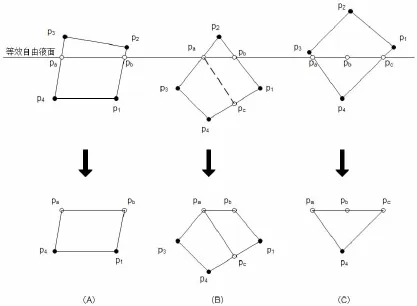
图3 自由液面交界处的网格截断及重构方法Fig.3 The gridding truncation method nearby the boundary of the free surface and the object
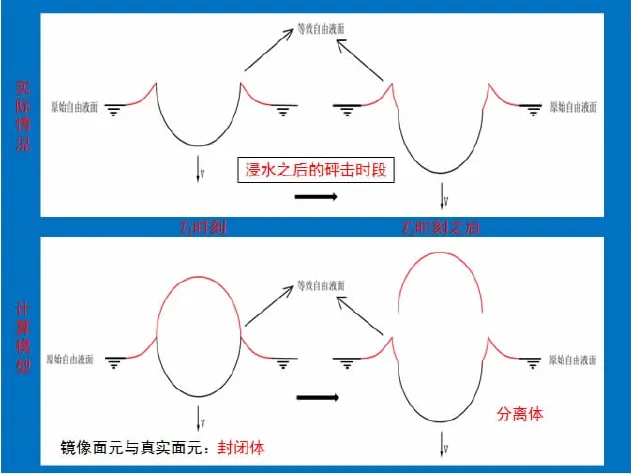
图4 坠物砰击后时段边界元模型示意图Fig.4 The BEM of the later entry time
1.4 砰击后时段算法适用性研究
按照上述的方法仅仅可以计算坠物未完全浸水的砰击时段,而对于坠物制高点低于等效液面之后的时段则无法进行计算。在物体完全浸水之后,短时间内物体的上表面事实上还没有被液体覆盖,因此在计算中物体的湿表面s与投影面s′将无法组成封闭面,本文所引用的无界流面元法则不能适用,在后续求解方程组的过程中会出现无解的情况。
如图4所示,T1时刻之后s与s′分离,之后便是本文所指的“后砰击”时段。
对此,本文提出了添加虚拟面元的方法,使入水“后时段”的砰击载荷计算得以实现,下图5是本文所设计的三种入水边界元模型。图中a是实际的入水边界元模型,b是添加的虚拟边界元模型,每个面都有两种颜色,其中棕色代表物体的触水湿表面。第一种模型根据实际情况对a图边界元模型加了一个上盖,并且划分边界元网格,即b图所示圆形结构。这样在T1时刻之后,a、b共同组成了一个闭合的边界元模型,经与抬升后的自由液面对称便可以形成两个闭合的边界元模型,符合理论要求。如果使用这样的水动力模型进行计算的话,实际上就是认为在半球入水之后液体立即将半球体吞没,即半球上盖之上被流体覆盖。第二种模型,实际上就是模拟了在T1时刻之后a的上缘与抬升后的自由液面间的液面形状,这一段液面上一定存在着分布源,它对流场性质有重要的影响,本文计算时将其视作湿表面的一部分,可以计算出其上的分布源强度,从而对a表面面元速度势进行修正,最后在计算试件垂向压力时并不是对a和b上的所有面元进行加权计算,仅仅考虑a上的面元压力,b仅仅是作为一个虚拟的湿表面。第三种模型类似于第二种,只是假想T1时刻后a上缘的自由液面成圆筒状,因此将b设计成了圆筒状的一层面元。
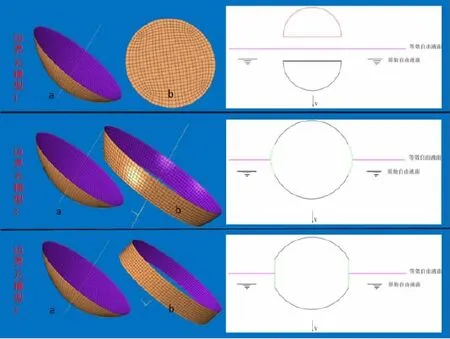
图5 3种虚拟边界元模型的添加实例Fig.5 3 adding methods for the virtual surface elements
2 砰击载荷的数值计算结果与试验比较
2.1 Alaoui刚性半球定常速垂向入水[15]
本文使用Abaqus/CAE程序建立了相应的边界元模型。半球的纵深H=77.34 mm,根据Nisewanger提供的半球入水自由液面升高公式计算可得在T1时刻半球恰恰完全浸没于水(半球底面恰与等效自由液面平齐)。对于18 m/s的情况来讲,T1=2.61 ms;对于20 m/s的情况,T1=2.41 ms。试验分别给出了6 ms和5 ms的时历曲线,因此可以断定T1之后的数值是完全浸没之后的数值(试件最高点低于等效自由液面),但是由于入水情况的瞬时性,半球周围的液体被拍击而溅向四周,在浸没之后的短时间内是不会将水下物体覆盖,从以往的试验中也可以观察到这种现象。这就提出了新的问题:T1时刻之后的湿表面的构成问题,即要探寻一种合适的水动力模型(边界元模型)来精确T1时刻之后的压力计算。
根据图5提出的三种添加边界元模型的方法进行砰击载荷求解,计算结果如图6-8所示。
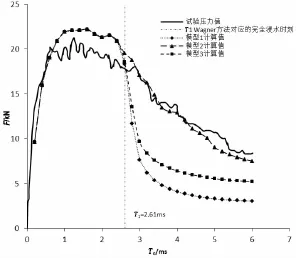
图6 18 m/s半球入水受力时历Fig.6 The force-time curve of the hemisphere for 18 m/s
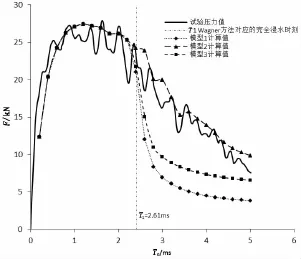
图7 20 m/s半球入水受力时历Fig.7 The force-time curve of the hemisphere for 20 m/s
可见使用边界元模型2的虚拟面元形式计算结果与实验匹配良好,所以对于半球入水“后时段”的砰击载荷计算可以采用该添加虚拟面元的方法进行计算。
3 结 语
(1)本文基于三维边界元方法,编写了可用于计算轴对称结构入水砰击载荷的计算程序,在自由液面处理方面继承Wagner液面抬升理论,引入“浸深因子”Cw以确定液面抬升高度,简化了自由液面处理方式,提高了程序计算效率。
(2)算法中考虑了网格运动,在自由液面附近对网格进行截断重构处理,精准了每一时间步对应的水下湿面积。
(3)使用该程序算法计算了Alaoui圆球体入水载荷,载荷计算结果与试验数据匹配良好,验证了本文计算程序的可行性与准确性;并从另一方面说明了线性自由液面对于砰击载荷计算有较好的适用性。
(4)提出了入水“后时段”的砰击载荷计算方法,扩大了传统的砰击载荷时历计算范围。
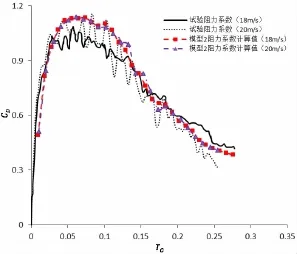
图8 半球阻力系数时历Fig.8 The resistance-coefficients-time curve of the hemisphere
[1]Wu G X,Sun H,He Y S.Numerical simulation and experimental study of water entry of a wedge in free fall motion[J]. Journal of Fluids and Structures,2004,19:277-289.
[2]Wu G X.Numerical simulation of water entry of twin wedge[J].Journal of Fluids and Structures,2006,22:99-108.
[3]Xu G D,Duan W Y,Wu G X.Numerical simulation of oblique water entry of an asymmetrical wedge[J].Ocean Engineering,2008,35(16):1597-1603.
[4]Scolan Y M,Korobkin A A.Three-dimensional theory of water impact:Part 1.Inverse Wagner problem[J].Journal of Fluid Mechanics,2001,440:293-326.
[5]Korobkin A A,Scolan Y M.Three-dimensional theory of water impact:Part 2.Linearized Wagner problem[J].Journal of Fluid Mechanics,2006,549:343-373.
[6]Faltinsen O M,Chezhan M.A generalized wagner method for three-dimensional slamming[J].Journal of Ship Research, 2005,49(4):279-287.
[7]Von Karman T.The impact on seaplane floats during landing[R].NACA TN 321.Oct.1929.
[8]戴遗山,段文洋.船舶在波浪中运动的势流理论[M].北京:国防工业出版社,2008:11-35.
[9]Prediction of impact pressure,forces,and moments during vertical and oblique water entry[R].NSWC.15,January,1977.
[10]Nisewanger C R.Experimental determination of pressure distribution on a sphere during water entry[J].NAVWEPS 7808, 1961.
[11]Faltinsen O M,Landrini M,Greco M.Slamming in marine applications[C].Journal of Engineering Mathematics,2004,48: 187-217.
[12]Krobkin A A,Pukhnachou V V.Initial stage of water impact[J].Annual Review Fluid Mechanics,1988,20:159-185.
[13]Takagi K,Dobashi J.Influence of trapped air on the slamming of a ship[J].Journal of Ship Research,2003,47(3):187-193.
[14]Sharov V F.Ship bottom impact upon wave[J].Sudostroyeniye,1958,4:5-9.
[15]Aboulghit EI Malki Alaoui,Alain Neme,Nicolas Jacques.Numerical and experimental studies of simple geometries in slamming[J].International Journal of Offshore and Polar Engineering,2011,21(3):216-224.
Numerical calculation of the slamming load for axisymmetric geometries during the later entry time based on generalized Wagner theory
ZHAO Jiu-long1,2,YAN Fa-suo1,FAN Lei3
(1.Harbin Engineering University,Harbin 150001,China;2.Shanghai Salvage Co./Ocean C&I,Shanghai 200129,China; 3.Texas A&M University,College Station,Texas 77840,USA)
A numerical code used for calculating the slamming load for axisymmetric geometries based on 3D BEM was mainly introduced.The 3D mechanical model and Wagner’s theory which considering the uplift free surface were both used in the numerical code.Cw which was called wetting factor was introduced to ensure the exact height of the uplift free surface.At the same time,the grid’s movement was also considered and along the interface between the geometry and the free surface one group of grids were modified for a precise wet area.The Nonlinear Bernoulli equation considering the grid’s movement was used for calculating the hydrodynamic pressure and the force could be obtained through integration.Besides,the conception of Virtual surface element was brought here so that the slamming load when the top point of the falling object was under the free surface could be achieved.That is to say,the traditional calculated time process was extended.At the same time,Alaoui slamming test was used to test the code’s validity.
axisymmetric geometries;slamming load;uplift of the free surface; grid’s modification;virtual surface element
TV131.2
A
10.3969/j.issn.1007-7294.2016.07.007
1007-7294(2016)11-1412-08
2016-04-07
赵九龙(1988-),男,工程师,E-mail:tcjiulong@sina.com;闫发锁(1977-),男,教授。
