数学建模思想与方法融入数理统计课堂教学的研究与实践

张学新

(湖北工程学院 数学与统计学院, 湖北 孝感 432000)



数学建模思想与方法融入数理统计课堂教学的研究与实践

张学新

(湖北工程学院 数学与统计学院, 湖北 孝感 432000)

摘 要：文章系统阐述了数理统计课堂教学融入数学建模思想与方法的必要性，指出把数学建模思想与方法融入数理统计课堂教学的关键在于教师把统计学作为一个为学习数学概念提供有意义环境的理想领域，培养学生的统计思想。教师要发展对数据的认识及统计软件分析能力，要做好数学建模材料的选择与预处理。通过实例展示把数学建模思想与方法融入数理统计课堂教学的若干实践。

关键词：数学建模思想方法; 统计思想; 数据开发; 统计软件技能;数理统计教学改革

历年美国国际大学生数学建模竞赛及交叉学科数学建模竞赛(MCM/ICM) )、全国大学生数学建模竞赛(CUMCM)与全国大学生统计建模竞赛(SUCM)中一些具有挑战性的建模实例，成为数理统计应用的经典材料。最近几年，数学建模促进《概率论与数理统计》的教学改革成为大学里一个突出的话题。文章是湖北工程学院统计学专业把数学建模融入数理统计教学改革实践的思考与总结。

1 概率论与数理统计的教学改革状况

上世纪90年，《概率论与数理统计》的教学在西方发达国家开始受到较大关注。美国、英国、法国、巴西等发达国家普遍认为，数理统计是大学里最重要的数量方法学科，但是它的教学日益面临挑战[1-3]。美国不少有名的统计教育家归纳统计学习中的困难，提出统计教育有关的问题，主张把教学内容、教学法与教学技术协调起来对统计指导思想和课程进行改革[4-7]。关于统计教学方法的改革，他们倡导把认知理论应用统计教学实践，通过问题解决方式，使教师与学生双方受益。他们注重强调统计教育的特色，诸如统计思想、主动学习、概念理解、纯数据、技术使用、集体学习、交流技能的统计教育的改革运动。改革后的课本编写不仅更多强调统计思想，概念理解，而且附录学生实践使用的数据，包括在网页存放数据集。在开发Java应用程序和新软件时考虑更多的给统计概念以交互、直观的解释。评价学生，则集中在学生的概念理解和统计思考能力方面。

在我国，随着社会对统计人才的需求日趋增长，对学生的实践能力的要求也在不断提高，迫使不少高校进行《概率论与数理统计》课程的教学探讨[8-10]，从教学目标、教学内容、教学方法、教学手段及对学生学习的评价方法等方面进行经验总结。其中不乏根据各自的培养目标和学生特点，进行思考、论证和实践[11]。

课堂上多媒体设备的广泛使用，也推动了《概率论与数理统计》课程的教学改革。教师如何指导学生探索应用课题，使学生凭借数学软件迅速实现个人的各种想法，在失败与成功中得到真知，引起诸多思考。许多文献研究提到案例教学、多媒体教学与实验教学[12-14]，也有提到融入数学建模思想的教学思路[15-19]，主要是对课程的内容增添了一些简明生动的应用问题，尽可能地用问题、事例来导入概念，用建模方法加案例的方式开设讲座，但缺乏对数学建模思想与方法融入《概率论与数理统计》课程教学的系统理论研究，较少涉及如何利用统计软件教学实训。我们在统计学专业教学中提出了“70%的理论+90%的实践操作”理念，结合建模素材大力强化统计专业软件的应用能力。几年的实践，使得《概率论与数理统计》的教学取得不少有益经验。2014荣获高教社杯全国大学生数学建模竞赛国家一等奖，2015荣获第三届泰迪杯全国大学生数据挖掘竞赛一个二等奖、两个三等奖。

2 数理统计课堂教学融入数学建模思想与方法的合理性

2.1统计模型可提升数学模型的表现

一个统计模型以数学方程形式对变量间的联系形式化，它描述一个或多个随机变量怎样与其它随机变量相互关联。给定可能的观测集X及关于X的概率分布P，统计模型就是有序对(X,P)，这是一个内在一致的概率假设集合，旨在给定观测到的数据x=(x1,x2,···xn)后，为随机机制提供一个“理想化”的概率描述。

一个纯数学模型不含随机的成分，输入与输出的关系以确定的方式完整地被捕获。纯数学模型在描述观测的、试验的或调查数据时是不实际的，通常在模型中确定性成分之外再吸收一些随机的成分，产生一个随机模型。

统计模型有助于估计观测数据中的不确定性和估计基于观测数据的计算中的不确定性，能提供一个简洁及容易理解的描述。统计模型可以通过多种形式，包括微分或理论模型，直接建立了理论模型与试验测量间的联系。特别地，数学建模中的一些参数未知时，必须通过数据估计，而数据是有测量误差的，数学模型中不可避免的含有不确定性因素。因此，在理解许多自然现象和社会现象时，除了数学，概率论、随机分析与统计是不能回避的，任何现实世界现象的真实模型必须把随机的可能性考虑进来，必须利用统计技术和过程。

总之，统计模型可以描述一个数学模型的数值输出特征来理解数学模型的行为；可以估计数学模型模拟自然系统重要特性的能力，并把这些信息反馈给建模过程，提升模型的表现；可以基于过去的统计信息，评估一个系统的概率的未来行为；可以估计复杂数学模型的输入参数。有时，一个系统引进随机性后，即使能给研究现象一个确定性的数学模型，但是一个统计模型能提供一个更简洁及更容易理解的描述。

2.2数学建模思想与方法的引入升华数理统计课堂教学

数学建模思想与方法融入数理统计课堂教学具有重要意义。

把数学建模思想与方法融入数理统计课堂教学，发展了一种创新教育，在这种教学模式下学生将掌握一套合适的量化现实世界问题的数学思想体系，协助学生发展有效地运用数学统计思想来解决问题的技能，更重要的是具备解释结果和进一步认识的能力。在简单的层面上，它促进学生进一步了解，当数学建模涉及统计学科现象中固有的变量时，它不可能建立起观察到的现象与表示它的抽象模型之间的任何联系。

数学建模思想与方法融入数理统计课堂教学有助于学生获得必要的资质，例如把现实问题转换为数学与统计问题的能力，帮助学生获得数学、《概率论与数理统计》学的清晰和直接的印象，它使学生认识到这些学习对生活是必要的。

数学建模思想与方法融入数理统计课堂教学激励学生以一种深刻方式思考数学、概率论与数理统计和计算机科学，使他们能够回忆起以前学过的重要概念，它使《概率论与数理统计》学的教学富有历史背景，促进数理统计课堂教学高质量的讨论。

3 数学建模思想与方法融入数理统计课堂教学的观念转变

数学建模思想与方法融入数理统计课堂教学首先要正确了解统计学思想与数学思想的差异，在《概率论与数理统计》课程的教学改革中，要树立这样的一种观念，数学内嵌于统计学，统计学是一个为学习许多数学概念提供有意义环境的理想领域。无论何时都应把统计适当应用于对标准概念的说明和扩展。

统计是一门方法论学科，它不是为自身而是为其他研究领域提供一套条理分明的观念与处理数据的工具。统计在考虑变异的普遍性下，提供处理数据的手段。聚焦变异给予统计学特别的内容，使得统计学不同于数学自身，也不同于其他数学科学，更重要的是统计学还有一种不同的思想——统计思想。

关于统计思想，美国统计协会(ASA)/美国数学协会(MAA)本科统计学联合委员会(1992)[20]的定义为：对数据的需求，数据生产的重要性，变异的无所不在性，对可变性的测量和建模。美国统计协会工作委员会(1993)则表述为：对不确定性和数据的变化以及它们对决策影响的欣赏，处理问题时科学方法的使用。Snee (1990)[21]把统计思想定义为一种思维过程，即认识到变化总在人们身边，并存在于人们所做的一切，所有工作是一个相互联系的过程系列：识别，定性，量化，控制和减少变化对工作改进的干扰。不同定义均表明，要把对变异的理解与统计过程作为统计的整体看待。理解(相信)统计的关联性，经常把数据与研究背景关联起来。例如，在管理中统计思想的体现在：具有过程定向的观念，理解变异(每个事情都有变异，变异的存在提供了一个过程改进的机会，改进源于减少变异，管理行为要在决策过程中考虑变异)，利用数据指导行动(实验数据是改进过程的关键等)。

虽然数学家以研究动机和问题来源经常依赖于应用背景，但是数学思想的最终焦点在抽象的形式，背景只是不相关细节的一部分，为了揭示先前隐藏的本质结构，随着抽象的深入，背景是必须要去掉的。与数学家一样，统计学家也寻找模式，模式最终在数据分析里，是否这些模式有意义，还是有价值，取决于这些模式的线索怎样与其它补充线索相互交织[22]。在数学里，背景模糊了结构；在数据分析中，背景则提供意义。如果去掉统计学的数学背景，保留下来的只是它的图案与背景间的相互作用，需要用统计思想去解释。

4 数理统计课堂教学中融入数学建模思想与方法的一些实践

4.1教师要熟练使用统计软件，发展师生统计思想能力

教师不仅要懂数据知识，更要熟练使用统计软件开发数据，会用计算机模拟数据。统计软件技能在整个数学建模思想与方法融入数理统计课堂教学的过程有着极其重要的作用，教师的统计软件使用能力将影响数理统计课堂的教学内容及教学方式。熟练的统计软件操作，带动课堂教学中各种相关数据的积极使用，带给学生有益的尝试与体验，能极大地开阔师生教学数理统计的视野。

4.2教师要重视关于数据的情境知识，创造生动的统计思想环境

传统的数理统计教学专注于传授统计调查有关的技能，给出数据只是为了练习画一个正确的分析图或提出狭窄的结构化的统计问题，忽视关于数据的情境知识及数据里包含的故事，限制了学生与数据交互作用、解释及从数据做出结论、质疑数据的机会。为此，教师必须树立对统计学的正确态度、观念和信仰。要信仰统计不简单地是数学的一个分支，而是有其独特的研究领域，它在应用上非常活跃。教师不能把《概率论与数理统计》的教学作为数学类课程讲授，而应着重培养统计学思想，发展对关键统计概念(例如数据，统计推断等)的理解，不侧重于数学公式的证明与推导等。

数学教学中，应用背景不很重要，数学老师能熟练地当场举例，而且这种即兴的例子经常有效。但是在数理统计教学里，即兴的例子经常不起作用，因为它们不能在模式与背景之间提供可信的相互作用。教数理统计就像教诗歌一样，图案与背景不可分割，教师必须准备真实图例，坚持统计概念来源于真实的问题。

【例1】方差的概念引入。

要即兴给出两个不同分布具有相同的期望并不容易，如果还要用图示清晰地反映出它们的显著发散性则更不容易。先想象一个物理学的情境，把点x的质点p(x)放在x轴上，x轴被一个放在均值μ位置的支点所支撑而不倾斜；然后保持μ位置的支点不变且x轴不倾斜寻找另一种分布。总体X1的分布是P(X1=3)=0.3,P(X1=4)=0.4,P(X1=5)=0.3，总体X2的分布是P(X2=1)=0.4,P(X2=2)=0.1,P(X2=6)=0.3,P(X2=8)=0.2，概率线条图见图1。

图1　均值为4的两个不同分布

这个例子很好的做到了数字、图案与背景的紧密联系，让学生直观的看到：(1)均值测度了概率分布的趋中位置，而方差测度了总变异；(2)两个分布的均值相同，但围绕均值的发散性显著不同。

【例2】概率密度曲线的峰态。

在讲授“分布的其他特征数之概率密度函数的峰度系数与偏态系数”时，拓展了一个典型实例(数据来源[23])，是美国第一国家公园旧费斯富尔喷泉。给出等待时间的一个核密度估计，使用Matlab做出图2。这里的两个峰态说明了什么呢？如果教师不懂数据，就只看到曲线有两个峰。实际上，内部喷发时间的双峰暗示两种不同的喷发，偏态偏高的部分表明其是主要区域的分布，它才是典型的等待时间。

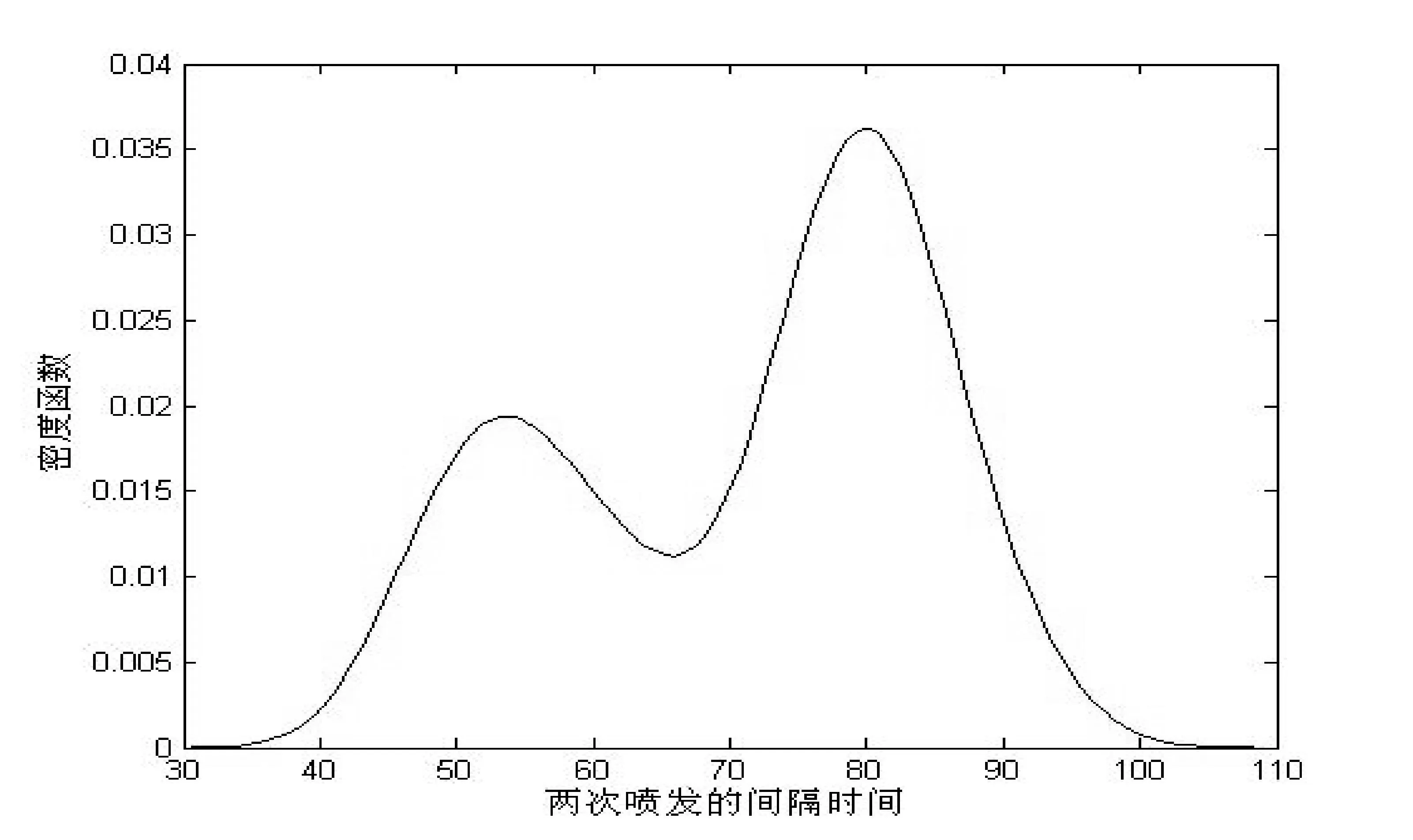
图2　旧费斯富尔泉等待时间的一个核密度估计

4.3重视用模拟及模拟的数据向学生演示难懂的统计概念

数学思想的终点在于揭示隐藏的本质结构，而数学模型是现实情形的模拟。这种把认识应用于数理统计教学中，特别重视用模拟及模拟的数据向学生演示难懂的统计概念。

【例3】从方差未知的正态总体随机抽取大小为10的样本，给出其均值90%的置信区间。

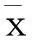
学生们惊讶的看到多于90次、少于90次的都有。趁机，教师指出“(1-α)%的置信区间在100次试验中，未必恰有100(1-α)%次包含了真值，但是，平均而言，在这样的大量的区间估计观测值中，至少有100(1-α)%次包含了真值。”

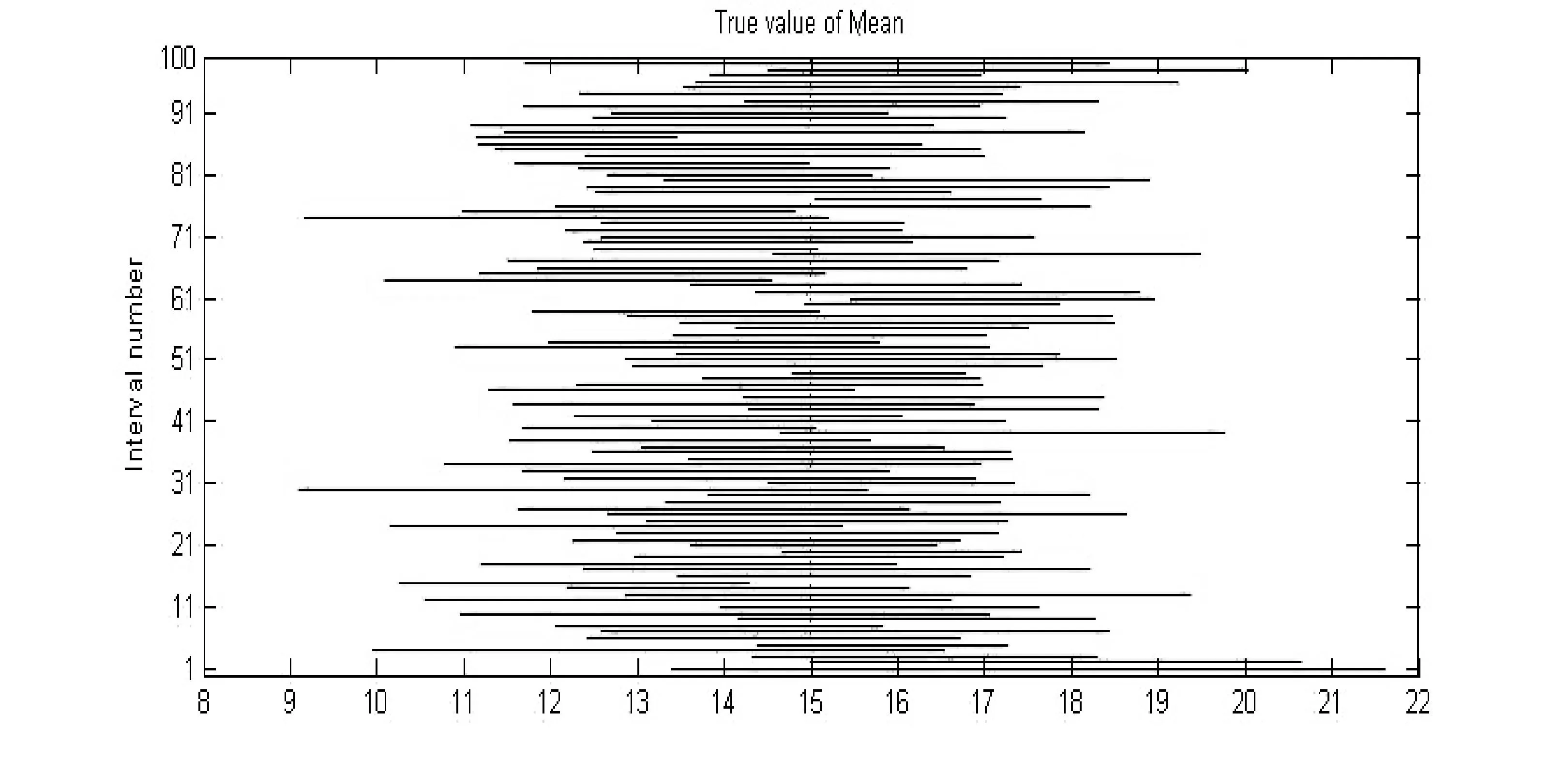
图3　 μ的90%置信区间

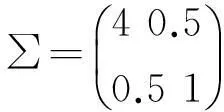
实践中，我们不只是把计算机作为有效的计算工具，还利用它提供可应用统计技术的环境，帮助学生澄清一些特别的概念。

4.4培养学生提出数字的、图形的推理和结论，并要求学生使用统计软件处理它们

数学建模中首先对现象做一般的观测，形成一个假设，再发展一个方法检验这个假设。融入这种思想方法就要培养学生提出数字的、图形的、符号的和口头上的推理和结论，并要求学生使用技术，包括统计软件、计算机和数据采集设备处理它们。

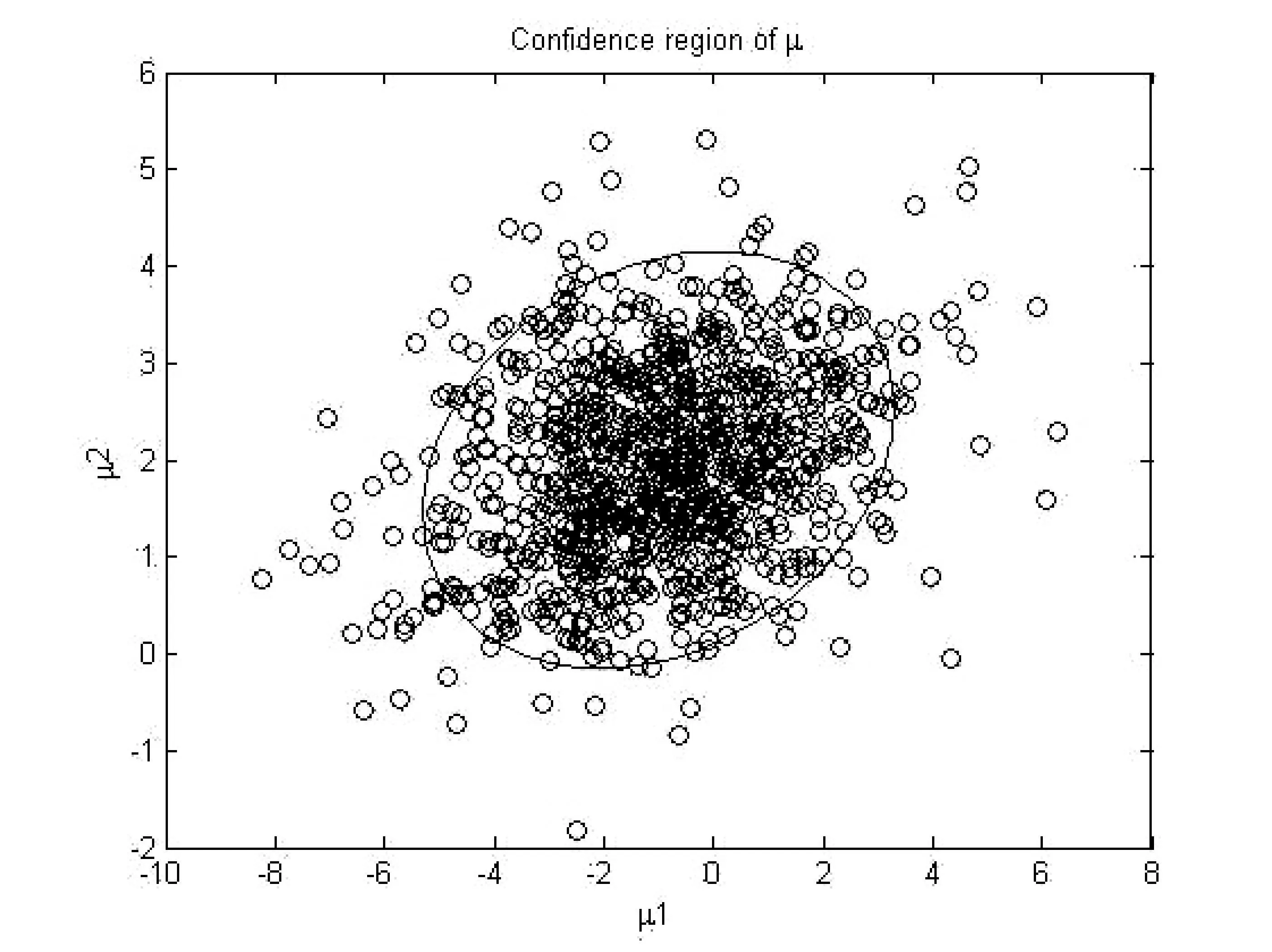
图4　二元正态分布均值的90%联合置信域

【例4】单个正态总体均值的检验。设从甲地发送一个信号到乙地，乙地接受到的信号值是一个服从正态分布N(μ,0.22)的随机变量，其中μ为甲地发送的实值信号，现甲地重复发送同一信号5 次，乙地接收到的信号值为8.05，8.15，8.2，8.1，8.25，设接受方有理由猜测甲地发送的信号值为8，问能否接受这种猜测。

一般教材处理时，归结为双边假设检验。讲解双边假设检验后，不失时机的启发学生：从样本观测值看，都是大于8的，能否提出H0:μ=8 vs μ>8的假设？然后要求学生利用Spss或Matlab软件完成右端检验。

为了便于统计软件进行科学计算、数据分析和提升学生交流能力，在建模过程中不过分调强数学形式主义。本例中，学生能用软件分析输出结果就达到基本目的。

%Matlab 右端检验

x=[8.05 8.15 8.2 8.1 8.25]′…;

[h,p]=ttest(x,8,0.05,′right′)

检验结果p-值 =0.0066，小于显著性水平α=0.05，拒接原假设。

这里重点理解为什么要右端假设检验，而不是死记针对各种数据类型的具体检验。

4.5引入建模题材，教会学生收集数据，产生数据和使用数据

数学建模竞赛宗旨在于培养学生解决实际问题的能力和创新精神，模型避免不了纷繁复杂的具体问题背景，经常会有大量数据需要统计处理。在实证分析的情形引入建模题材，要教会学生收集数据，产生数据和使用数据。

【例5】 医院眼科病床安排问题(全国大学生数学建模竞赛(http://www.mcm.edu.cn/)之2009年赛题)中的“分布的拟合优度检验”教学的部分设计。

该题目很长，附录了某医院眼科从2008年7月13日至2008年9月11日的每天出院人数和入院人数统计表及61天各类患者门诊数据，希望求解三个问题：

(1)建立评价指标体系，评价现有病床安排模型的优劣。

(2)依据住院部目前的情况，建立合理的病床安排模型，通过第二天拟出院的病人数确定第二天应安排入住的病人，并利用第(1)问的指标体系评价所建立的模型。

(3)利用当时住院病人及等待住院病人的数据，预测病人大致住院的时间段并在病人门诊时即告之。

课堂教学解析：

在引入该数学建模题材前，教师须对题目进行节略改编，使得问题的陈述更像一般的数理统计问题，改编后的题目要彰显“从数据开始”的统计思想，突出了“分布拟合检验”的数理统计知识点。

第一，术前住院时间过长，白内障病人的入院时间影响了病床有效利用率；第二，从2008年7月13日至2008年9月11日平均每天到门诊看病的人数为8.6885人，平均每天出院人数为8.1163人，平均看，每天到门诊看病的人数大于每天出院的人数，这导致了等待住院病人队列越来越长。第三，病人术前住院时间是确定的，依入院时间而定，病人住院时间中只有术后住院时间x是随机的，可以从正态分布 、T分布或埃尔朗分布等角度去拟合检验。

每天各类病人到达人数是随机的。为了模拟产生2008-9-12至2008-9-25每天各类病人的就诊人数，模拟每日出院人数，需要对每类每日病人到达人数，每日出院人数进行分布检验。接着教师提出争论：各类病人术后住院时间能否考虑指数分布拟合？请同学们回忆指数分布的重要特性，无“记忆”性后，给出回答：不能。

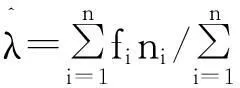
使用的统计软件，Matlab工具箱，Chi2gof，Sas 函数poisson(p,n)等之一，对统计的 61天青光眼门诊数据的分布拟合见表1。

表1　每天青光眼门诊病人到达数的Poisson分布检验

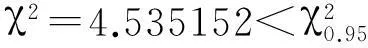
对其它类每日病人到达人数做分布拟合检验。结果表明各类患者到达人数分别服从不同参数的Poisson分布。因而，每日出院人数是服从参数为λ=8.8的泊松分布P(8.8)。

对数学建模材料的选择，难度及统计任务都要适中，解决问题的方法多样且能为学生所用。

【例6】葡萄酒评价问题(http://www.mcm.edu.cn/problem/2012/cumcm2012problems.rar)中的“数据分析”教学的部分设计。

这个2012高教社杯全国大学生数学建模竞赛题目的背景是，欲聘请一批有资质的评酒员进行品评以确定葡萄酒质量。每个评酒员先对葡萄酒品尝，然后给出分类指标得分，以各种葡萄酒的总得分定义葡萄酒的质量。已知葡萄酒的质量与酿酒葡萄的好坏有关，葡萄酒和葡萄的质量也能通过它们的检测的理化指标反映一部分。某一年份一些葡萄酒的评价结果放在附件1，该年份这些葡萄酒的和酿酒葡萄的成分数据分别放在附件2和附件3里。希望建立数学模型解决下列问题：

(1)分析两组评酒员的评价结果的差异性，选出较可信的一组。

(2)利用酿酒葡萄的理化指标和葡萄酒的质量数据评定这些酿酒葡萄的级别。

(3)分析酿酒葡萄与葡萄酒的理化指标间的关系。

(4)分析酿酒葡萄和葡萄酒的理化指标如何影响葡萄酒的质量，并回答可否用葡萄和葡萄酒的理化指标来评价葡萄酒的质量。

课堂教学解析：

(1)启发学生联想统计概念

问题(1)要求比较两组评价结果的是否存在差异，并建立合理的评价模型以判断两组结果在可信程度方面的优劣，可归为两样本均值检验问题。

让学生给两组评酒员对酒样评分的平均值画个柱状图或走势图比较分析。缺点：不深刻，缺乏必要的统计模型检验步骤。

再探索：先对数据求均值，使用检验T方法，为此需要对红、白葡萄酒的得分均值是否服从正态分布进行检验。正态分布的检验有许多方法，这里使用正态图P-P检验方法(调用normplot(X)，其中数据X是列向量)，从散点图近似于直线y=x，可以认为评酒员对红白葡萄酒的评分均值都服从正态分布。接下来做两个正态总体均值之差的检验就容易了。

也可以先用SPSS对缺失数据和异常数据进行处理，再进行多配对样本的非参数检验(Kendall 协同系数检验，曼-惠特尼U检验(等同于在Matlab中调用p=ranksum(x,y))等)。

比较两组评酒员对红白葡萄酒平均分总体均值的置信区间，空间第二组的区间长度短些，据此可以说第二组的评酒员评价结果更可信。

(2)引导学生寻找和表达统计规律，兼顾适当的数学复杂性

问题(2)首先要根据酿酒葡萄的理化指标和葡萄酒的质量指标确定分级的原则，然后依据原则采用相应的方法建立分级模型，最后通过模型求解给出3-5等级别的划分或分类。可选的建立分级模型的方法有主成分分析、因子分析、聚类分析(K-means聚类分析和模糊聚类分析)、回归分析和综合评价(模糊数学评价)等。

问题(3)酿酒葡萄和葡萄酒分别存在多个理化指标，考虑使用典型相关分析，或者偏相关回归分析。再者，用多项式曲线拟合的方法，找出一种适当的经验函数关系描述酿酒葡萄与葡萄酒之间相关关系。比如，利用统计软件(Matlab、SPSS) 对酿酒葡萄的理化指标关于葡萄酒的理化指标进行1次至3次多项式曲线拟合比较。

图5展示了红酿酒葡萄理化指标关于红葡萄酒理化指标的多项式拟合情况，其中一次多项式较好。对白酿酒葡萄理化指标关于白葡萄酒理化指标的多项式拟合，结果类似。于是得出，酿酒葡萄与葡萄酒的理化指标呈线性正相关。

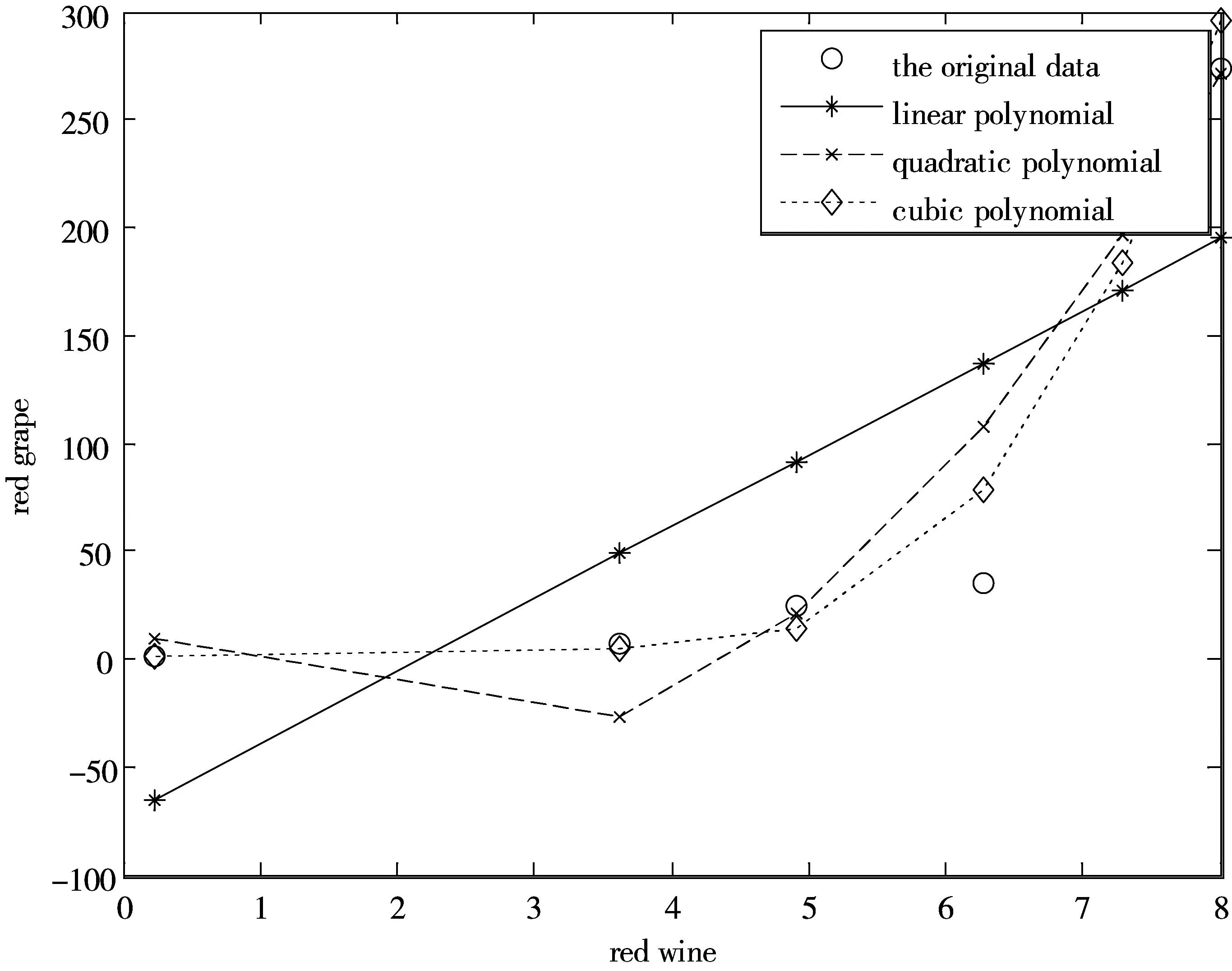
图5　红酿酒葡萄对红葡萄酒理化指标的多项式曲线

问题(4)论证是否可以利用酿酒葡萄和葡萄酒的理化指标评价葡萄酒的质量。首先考虑在前问的基础上，筛选出与葡萄酒质量相关性最强的酿酒葡萄与葡萄酒理化指标，然后建立多元线性回归模型，通过该模型及回归系数是否统计显著来对葡萄酒质量做评价。为了评价模型的表现，可以把样本随机分为两部分，一个子样本用于建立线性回归方程，另一个子样本用于对模型的可行性进行验证。

或者，设A表示酿酒葡萄的理化指标，B表示葡萄酒的理化指标，y表示葡萄酒质量，作为试验指标。考虑有交互作用的双因素方差分析，确定影响葡萄酒的主次因素。

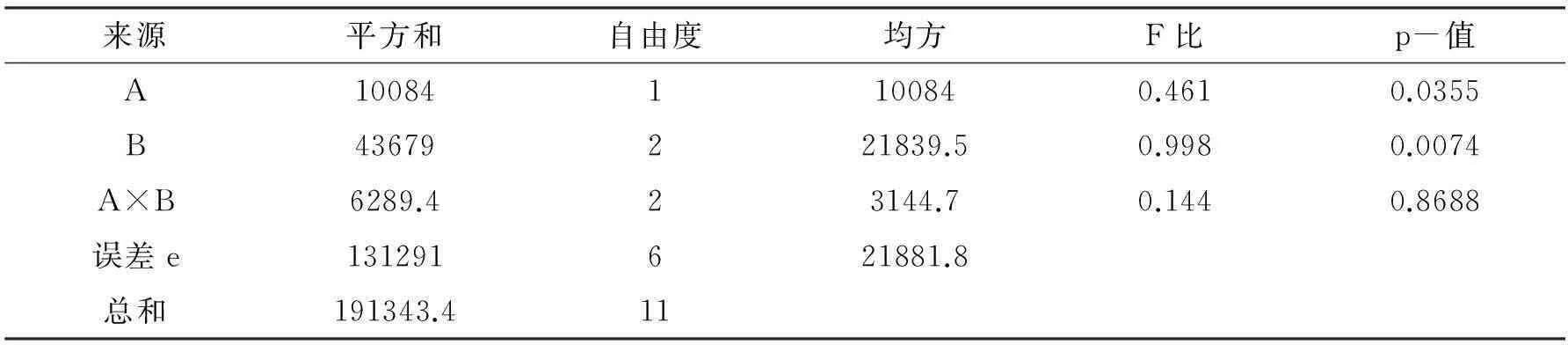
表2　双因素方差分析表

由表2可知，在0.5的显著性水平上，因素A及因素B对试验指标具有显著的影响，但交互作用A×B不显著。又因素B相应的p-值比因素A相应的p-值小，据此可以认为酿酒葡萄的理化指标对葡萄酒质量影响相对葡萄酒的理化指标更显著。

5结语

数学建模题的数据具有大量性、复杂性等特点，为基于统计软件应用的数理统计教学改革提供了很好的机遇，在《概率论与数理统计》教学中依据内容适当融入数学建模思想方法是培养学生解决现实问题的有效手段。设计这样的课程是一个挑战，既要能为数理统计课堂教学使用，培养学生使用统计模型的能力，同时保留一定的数学复杂性。把数学建模材料引入数理统计课堂教学中要注意：

(1)教师要充分准备，提前准备适宜的教学讲义；(2)对问题合理的抽象和量化、引入随机变量；(3)有策略地使用适当的统计软件，保证学生能够用统计软件解决实际问题，给学生体验成功的机会；(4)多角度地引导学生寻找和表达统计规律。

总之，把数学建模思想与方法融入数理统计课堂教学，尽量以较少的数学理论、以较多的统计方法换取学生更多的关注数据与基本概念，鼓励学生探索概念的含义，发展学生使用统计软件处理数据的能力。

参考文献：

[1] Moore, D. S. New pedagogy and new content: the case of statistics[J]. International Statistical Review,1997, 65(2):123-165.

[2] Garfield, J. , & Ben-Zvi, D. How students learn statistics revisited: A current review of research on teaching and Learning Statistics[J]. International Statistical Review, 2007, 75(3):372-396.

[3] Watson,J. Assessing statistical thinking using the media[A]. InI. Gal&J. B. Garfield. The Assessment Challenge in Statistics Education[C]. Amsterdam: IOS Press and The International Statistical Institute,1997:107-121.

[4] Garfield, J. , & Ahlgren, A. Difficulties in learning basic concepts in probability and statistics: Implications for research[J]. Journal for Research in Mathematics Education, 1988,19(1):44-63.

[5] Garfield, J. How students learn statistics[J]. International Statistical Review, 1995,63(1):25-34.

[6] Ben-Zvi,C. Towards understanding the role of technological tools in statistical learning[J]. Mathematical Thinking and Learning, 2000, 2(1&2):127-155.

[7] Smith,T. M. F. ,& Staetsky,L. The teaching of statistics in UK universities[J]. Journal of Royal Statistical Society, 2007, 170(3):581-622.

[8] 李明. 概率论与数理统计教学方法之体会[J]. 统计教育, 2006, (7): 22-23.

[9] 马学思, 李明. 《概率论与数理统计》的教学改革[J]. 统计与决策, 2011, (13).

[10] 邓华玲,傅丽芳等. 概率论与数理统计课程的改革与实践[J]. 大学数学, 2004,20(1):34-37.

[11] 周兴才. 应用型本科院校概率论与数理统计教学研究[J]. 襄樊学院学报, 2011, 32(5): 60-63.

[12] 陈建兰,吴明,孙伟良. 概率论与数理统计教学改革的探讨[J]. 杭州电子科技大学学报, 2005, (06): 58-60.

[13] 周宗好. 提升概率统计课堂教学效果的方法研究[J]. 黄山学院学报, 2013, 15(3):107-109.

[14] 王文文,张明. 浅谈典型案例的选取在概率论与数理统计教学中的重要性[J]. 大学教育, 2013, (5): 75-76.

[15] 叶林,邓筱红. 将数学建模思想、方法融人概率论与数理统计课程教学的一点尝试[J]. 工程数学学报2003, 20(8):93-96.

[16] 王庚. 数学建模与数学实验课程的探索、实践与收获[J]. 高等数学研究2007, 10(1):101-102.

[17] 刘琼荪, 钟波. 将数学建模思想融入工科“ 概率统计”教学中[J]. 大学数学, 2006, 22(2): 152 -154.

[18] 李晓毅, 徐兆棣. 概率统计教学与数学建模思想的融入[J]. 沈阳师范大学学报(自然科学版), 2008, 26(2):245-247.

[19] 刘蓉. 概率论与数理统计"教学改革之探索[J]. 长春理工大学, 2010, 5(7):132-133.

[20] Cobb,G. Teaching statistics,in heeding the call for change: suggestions for curricular action[A]. L. A. Steen, MAA Notes[C]. Washington, DC: Mathematical Association of America,1992,(22):3-34.

[21] Snee,R. Statistical thinking and its contribution to total quality[J]. The American Statistician, 1990,44(2):116-121.

[22] George W. Cobb and David S. Moore. Mathematics, statistics, and teaching[J]. The American Mathematical Monthly, 1997, 104(9): 801-823.

[23] Azzalini,A. and Bowman,A. W. A look at some data on the Old Faithful geyser[J]. Applied Statistics,1990,39:357-365.

The Theory and Practice of Integrating the Idea of Mathematical Modeling into the Teaching of Mathematical Statistics Curriculum

ZHANG Xue-xin

(SchoolofMathematicsandStatistics,HubeiEngineeringUniversity,Xiaogan,Hubei, 432000,China)

Abstract:The necessity of integrating ideas of mathematical modeling into Mathematical Statistics course was systematically discussed. Some keys to merge the idea of mathematical modeling into the teaching of mathematical statistics curriculum were present as follows: Firstly, statistics to be treated as an ideal field to provide a meaningful context for the learning of many mathematical concepts,to foster students' statistical thinking by the teacher,Secondly,to develope the teacher's ability to analyze data using software packages must be strengthened, Also, the selection and pretreatment of mathematical modeling materials should be well-prepared, Finally the results achieved with practice of this curriculum's reform were demonstrated by examples.

Key words:Mathematical modeling thinking method; Statistical thinking; Data exploring; Statistical software skills ;Teaching reform and practice in Mathematical Statistics

中图分类号:G642

文献标识码：A

文章编号：G6421008-9659(2016)01-063-09

[作者简介]张学新(1966-)，男，湖北宜城人，博士，副教授，主要从事概率论与数理统计方法应用研究。

[基金项目]湖北省教育科学“十二五”规划研究课题(2014B221)；湖北工程学院2014年度教学研究项目。

[收稿日期]2015-10-05