中心修正增量主成分分析及其在文本分类中的应用

2016-05-04陈素芬曾雪强

中文信息学报 2016年1期

关键词：协方差增量类别

陈素芬，曾雪强

(1. 南昌工程学院信息工程学院，江西南昌 330099；2. 南昌大学计算中心，江西南昌 330031)

中心修正增量主成分分析及其在文本分类中的应用

陈素芬1，曾雪强2

(1. 南昌工程学院信息工程学院，江西南昌 330099；2. 南昌大学计算中心，江西南昌 330031)

增量式学习模型是挖掘大规模文本流数据的一种有效的数据处理技术。无偏协方差无关增量主成分分析(Candid Covariance-free Incremental Principal Component Analysis， CCIPCA)是一种增量主成分分析模型，具有收敛速度快和降维效果好的特点。但是，CCIPCA模型要求训练数据是已经中心化或中心向量固定的。在实际的应用中，CCIPCA往往采用一种近似的中心化算法对新样本进行处理，而不会对历史数据进行中心化修正。针对这一问题，该文提出了一种中心修正增量主成分分析模型(Centred Incremental Principal Component Analysis， CIPCA)。CIPCA算法不仅对新样本进行中心化处理，而且会对历史数据进行准确的中心化修正。在文本流数据上的实验结果表明，CIPCA算法的收敛速度和分类性能明显优于CCIPCA算法，特别是在原始数据的内在模型不稳定的情况下，新算法的优势更为明显。

主成分分析；中心化修正；流数据；维数约减；增量学习

1 引言

流数据是近年来出现的一种新型的数据类型，在许多应用领域出现频繁，表现形式各异。与传统的数据类型相比，流数据具有如下特点：实时到达，速率多变；连续到达，次序独立；规模宏大，不能预知其极值；数据一经处理，除非特意保存，否则不能被再次取出处理[1-3]。由于流数据环境实际应用的需求，在流数据上进行在线监测、相关趋势的分析和预测、联机分析等研究工作受到了越来越多的重视。例如，网页点击流的分析，信息系统的入侵检测以及传感器网络的管理等环境中，有很大部分的应用需要对流数据进行及时的在线处理，从而获得尽可能短的响应时间。

数据的高维性是现代机器学习任务经常要面对的情况。与传统机器学习任务类似，高维或超高维的特征空间会对流数据的学习算法带来困难。维数约减(Dimension Reduction)将原始的高维特征变换到低维空间并尽可能降低无关和冗余特征的影响，可以提高建模的计算效率和泛化能力。在众多的维数约减方法中，主成分分析(Principal Component Analysis: PCA)是其中最为常见并被广泛应用的模型之一[4]。PCA的优化目标是寻找一个能尽可能保持原始数据信息(方差)的低维空间。传统的PCA以批量方式(Batch Mode)工作，即需要读入全部训练数据后再进行建模。但当原始数据的特征维数或样本数量过多时，批量方式的PCA会因为计算量过大或内存不足而无法工作。

解决该问题的一个可行的办法是设计一种增量式学习(Incremental Learning)的增量主成分分析(Incremental PCA: IPCA)模型。关于IPCA模型，国内外已有较多的研究工作[4-6]，现有的工作大致可以分为两类：协方差相关模型和协方差无关模型。协方差相关IPCA模型，需要随着样本的增加而增量的估计协方差矩阵，再由此计算出新的主成分。不同的协方差相关IPCA模型的区别主要在于其估计协方差矩阵的计算方式不同；而协方差无关IPCA模型可以避免对协方差矩阵的估计，直接采用新样本对得到的PCA主成分进行增量式的修正，这样可以减少模型的计算和存储的开销。在已有的协方差无关IPCA模型中，无偏协方差无关增量主成分分析(Candid Covariance-free Incremental Principal Component Analysis， CCIPCA)是其中收敛速度最快和效果最好的方法之一[7-8]。

和传统的PCA模型一样，CCIPCA方法有一个很强的假设前提，要求训练数据是已经中心化或中心向量固定的。在实际的应用中，CCIPCA一般会采用一种近似的中心化算法，即只对新进入的样本进行准确的中心化，而不对历史数据进行中心化修正。这样的中心化算法在数据内在模型变化不大的时候，有较好的效果；但是在其他情况下，数据没有准确中心化会明显降低IPCA模型的性能。目前已经有一些研究工作注意到了IPCA模型中的准确中心化的问题。例如，Ross等人基于SKL(Sequential Karhunen-Loeve)算法提出了一种中心修正的IPCA算法[9]；Duan和Chen提出了一种批量更新的中心修正IPCA算法[10]。但是这些研究工作都是对协方差相关IPCA模型的改进。目前还没有研究工作提出针对协方差无关IPCA模型的准确中心化修正的改进算法。

为了解决这一问题，我们提出了一种中心修正增量主成分分析(Centred Incremental Principal Component Analysis，CIPCA)模型。CIPCA算法不仅对新进入样本进行中心化处理，而且会对历史数据进行准确的中心化修正。在文本流数据集Reuter-21578上的实验结果表明，CIPCA算法的收敛速度和分类性能明显优于CCIPCA算法。新算法的优势在数据的内在模型不稳定的情况下更为明显。

本文组织如下：第一部分是引言；第二部分介绍IPCA模型的相关概念；第三部分对CIPCA模型的原理进行详细的阐述；实验结果与分析在第四部分中说明；最后一部分是结束语。

2 增量主成分分析

维数约减将原始数据从高维特征空间变换到低维空间，可以提高数据挖掘模型的计算效率和泛化能力。作为一种常见的无监督维数约减模型，主成分分析(Principal Component Analysis， PCA)的优化目标是寻找一个能尽可能保持原始训练数据信息(方差)的低维空间[11]。给定n个中心化的p维训练样本x(1),x(2), …,x(n)，PCA希望找到能保持最多方差信息的方向w。经过一些简单的推导，PCA的优化目标可以表示为式(1)。

(1)

其中，协方差矩阵如式(2)所示。

(2)

根据PCA成分之间的正交性要求，K个PCA投影方向就是协方差矩阵C的前K个特征向量。

作为一种维数约减方法，PCA将原始数据投影到K维子空间(一般K远小于p)。我们可以在变换后的低维空间进行进一步的数据挖掘和分析。PCA的具体求解一般采用奇异值分解(Singular Value Decomposition，SVD)[11]，其计算复杂度为O(η3)，其中η=min(p,n)。很明显，在样本数量和特征维度都很大的情况下，PCA算法的实际使用会由于计算量过大而出现困难。

为了适应大规模数据的应用要求，增量主成分分析模型(IncrementalPCA，IPCA)是一个较好的解决办法。现有的IPCA模型的相关研究工作可以分为协方差相关模型和协方差无关模型两大类[4-6]。随着样本的增加，协方差相关IPCA模型采用增量的方式更新对协方差矩阵的估计，再基于更新后的协方差矩阵计算得到新的主成分。不同的协方差相关IPCA模型的区别，主要在于协方差矩阵的增量计算方式的不同。无论采用何种计算方法，这一类模型的缺点是增量计算协方差矩阵的计算和存储开销比较大。而协方差无关IPCA模型直接用新样本对已有的PCA主成分进行增量式的修正；可以避免对协方差矩阵的重新估计。在已有的协方差无关IPCA模型中，无偏协方差无关增量主成分分析(CandidCovariance-freeIncrementalPrincipalComponentAnalysis，CCIPCA)模型是其中降维效果和收敛速度均比较好的方法之一[7-8]。

基于式(1)，CCIPCA定义了一个新的变量v=λw=Cw。给定n个样本的情况下，对v的估计v(n)可以按式(3)进行近似计算。

(3)

其中w(i)是对w的第i步的估计值。

如果能得到v的值，那么w就可以通过w=v/‖v‖计算得到，其对应的特征值λ=‖v‖。根据v和w的关系，构造增量递推公式的一个合理做法是用w(i-1)代替w(i)，用来计算当前的v(i)。这样，CCIPCA将公式(2)改写为式(4)。

(4)

另外，为了控制当前样本相对于历史数据的权重，CCIPCA还引入了一个遗忘参数(amnesic parameter)l。对式(4)进行修正后，CCIPCA最终的增量公式如式(5)所示。

(5)

3 中心化修正的增量主成分分析

和传统PCA模型一样，CCIPCA假设训练数据是已经中心化或中心向量固定的。为了满足这一要求，在实际的应用中CCIPCA会采用一种近似的中心化算法，即只对新进入的样本进行准确的中心化，而不对历史数据进行中心化修正。这样的中心化算法在数据内在模型变化不大的时候，有较好的效果；但是在其他情况下，数据没有准确中心化会明显降低IPCA模型的性能。为了解决这一问题，我们提出一种中心修正增量主成分分析(Centred Incremental Principal Component Analysis，CIPCA)模型。CIPCA算法不仅会对新进入的样本进行中心化，而且会对历史数据进行准确的中心化修正。

(6)

在样本均值已知的情况下，对当前新进入样本的中心化处理只需要简单的将样本向量减去均值向量。但是，对历史数据的中心化将会麻烦很多。随着样本的不断增多，当前的总体样本的均值是在不断的变化的；这样对历史数据的中心化就需要进行修正。在历史数据不能保存的情况下，我们就需要直接在IPCA的增量递推公式中考虑历史样本的中心化修正问题。

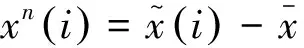
(7)

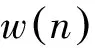
(8)

增量递推的式(8)只能解决第一主成分的计算问题，为了求取高阶PCA主成分，我们需要引入新的计算方法。我们注意到，PCA的各个主成分之间是相互正交的[11]；那么我们可以利用正交互补空间的性质，引入一种快速的计算方式。相似的计算方法已经被CCIPCA和一些类似的增量学习模型采用[7, 13-14]。

(9)

(10)

和CCIPCA算法一样，我们提出的CIPCA算法的计算复杂度是O(NKp)，其中N是样本数量，p是样本的特征维数，K是要得到的主成分的个数。在增量计算的过程中，CIPCA算法除了要存储当前的特征向量外，只需要存储样本均值向量和样本个数。因此，从计算复杂度和存储复杂度看，CIPCA算法都可以适应大规模数据的应用任务。CIPCA算法的具体的伪代码在图1中给出。

图1 中心修正增量主成分分析算法

4 实验结果与分析

4.1 实验数据集

本文采用由路透公司采集的1987年的新闻稿组成的Reuters-21578文集作为实验数据集。Reuters-21578是一个在文本挖掘领域被广泛采用的数据集[15]。虽然已有的在Reuters-21578文集上的大部分研究工作，只是将其作为一个普通的数据集来使用；但Reuters-21578文集实际上是一个典型的流数据集，因为其中的每一篇文档都一个时间戳。

在除去一些损坏的文档后，将训练集和测试集合并在一起，我们总共得到了11 359篇文档。这些文档分别属于120个类别，但文档的类别分布非常不平均。最常见的类别有3 986篇正例文档，而大部分类别(97个类别)的正例文档不足100篇。在本文的实验中，我们选用了最常见的两个类别earn和acq，他们的正例文档数分别为3 986和2 448。

对文档的处理步骤包括：去除数字和停用词，字母全部转为小写，采用Porter算法进行词干化处理。最终，我们得到了22 049个词，并采用了ltc权重进行文档的表示。实验在一台DELL的PC工作站上运行，硬件配置为24×Intel(R)Xeon(R)CPUX5680 3.33GHz，64G内存。实验的程序采用JAVA语言进行编码，代码中引用了开源机器学习工具箱WEKA[16]。

4.2 收敛速度分析

我们在earn和acq两个类别上，对比了CIPCA和CCIPCA的收敛速度。首先，所有的文档按照时间戳的先后进行排序；然后，我们从每个类别中分别选取了前1 000个正例文档；最后，这些文档被等分为20个数据块，每个数据块有50篇文档。我们将这些文档按照顺序加入到IPCA模型中，并且为每个数据块记录一个模型的收敛得分。

图2 CIPCA和CCIPCA的第一特征向量的收敛曲线

从图2中我们可以看出，CIPCA和CCIPCA总体上都会随着数据的增加而收敛。在类别earn上，CIPCA表现出比CCIPCA具有更快的收敛速度；而随着样本的增多，两个算法表现出了基本相同的收敛曲线。这说明，中心化修正的效果在数据样本比较少的情况下具有比较明显的效果；而当数据的内在模型稳定的时候，中心化修正的效果不明显。

我们还可以发现，CIPCA在类别acq上表现出了明显优于CCIPCA收敛性能。我们认为这是因为，当数据的内在模型不是很稳定的时候，样本均值向量就会有比较大的变化，那么中心化修正就能明显提升IPCA算法的性能。就像Weng指出的，IPCA算法在内在模型不稳定的数据流上的性能不佳[7]。因为数据的内在模型的剧烈变化，会使得IPCA模型的收敛出现问题。我们的实验结果也证实了这一观点。但是，从实验结果看，CIPCA在收敛鲁棒性方面要优于CCIPCA。

4.3 分类性能分析

在Reuters-21578数据集上已有的研究工作，一般会采用交叉验证或随机抽样的方式将文本的顺序打乱，再进行文本分类实验[15]。为了能更好的模拟真实的数据流的情况，我们设计了一个新的实验步骤。首先，我们将所有的文档按照时间戳的顺序等分为20个数据块，每个数据块大约有577篇文档；然后将这些数据块依次加入IPCA模型，进行模型训练；最后将已经加入IPCA模型的数据作为训练集，将当前的下一个数据块作为测试集，再采用IPCA进行降维、训练分类模型并记录最终的分类性能。这样，除了第一个数据块，我们可以为每一个数据块记录一个分类性能的结果。

我们采用了k近邻(kNearestNeighbout，kNN)分类器作为分类模型，其中的参数k=1。每个类别均作为一个二分类(binaryclassification)任务，正例的类标为1，负例为-1。采用常用的F1值记录最终的分类性能。我们在图3中给出了具体的CIPCA和CCIPCA在类别earn和acq上的分类结果，其中图3的上半部分是对应数据块的正例文档数。参数K和l的值分别设置为5和2。

图3 中心修正的增量主成分分析算法

我们从图3的结果可以发现，CIPCA在类别earn上的性能与CCIPCA类似；而在类别acq上，CIPCA的性能要明显优于CCIPCA。我们认为这是与数据的内在模型的稳定程度相关的。类别earn的数据的内在模型较为稳定，那么对历史数据的中心修正的效果会不明显。而当数据的内在模型变化较为剧烈的时候，CIPCA就会表现出明显优于CCIPCA的性能。这也是我们观察到CIPCA的性能在类别acq上优于CCIPCA的原因。另外，这与我们在前一小节分析模型的收敛速度时的结论是一致的。

另外我们可以发现，两个IPCA模型在类别earn的性能总体上要优于在类别acq上的性能。这也说明了类别earn的数据内在模型较为稳定，比较有利于增量学习算法的建模。而类别acq的数据内在模型变化较为剧烈，不利于IPCA模型的收敛。

5 结束语

无偏协方差无关增量主成分分析(CandidCovariance-freeIncrementalPrincipalComponentAnalysis，CCIPCA)是一种协方差无关的增量主成分分析模型，具有收敛速度快和降维效果好的特点。但是，CCIPCA模型要求训练数据是已经中心化或中心向量固定的。在实际应用中，CCIPCA一般会采用一种近似的中心化算法，只对新进入的样本进行中心化处理，而不对历史数据进行中心化修正。这样的中心化算法在数据的内在模型变化不大的时候，有较好的效果；但是在其他情况下，数据没有准确中心化会明显降低IPCA模型的性能。

为了解决历史数据的中心化修正问题，本文提出了一种中心修正增量主成分分析模型(CentredIncrementalPrincipalComponentAnalysis，CIPCA)。CIPCA算法不仅会对当前新进入样本进行中心化，而且会对历史数据进行准确的中心化修正。在文本流数据集上的实验结果表明，CIPCA算法的收敛速度和分类性能优于CCIPCA算法。特别是当数据的内在模型不稳定的情况下，CIPCA算法的优势更为明显。

[1]GolabL,JohnsonT,ShkapenyukV.Scalableschedulingofupdatesinstreamingdatawarehouses[J].IEEETransactionsonKnowledgeandDataEngineering, 2012, 24(6): 1092-1105.

[2]AusterberryD.Thetechnologyofvideoandaudiostreaming[M].FocalPress, 2005.

[3]BabcockB,BabuS,DatarM,etal.Modelsandissuesindatastreamsystems[C]//Proceedingsofthe21thACMSIGMOD-SIGACT-SIGARTsymposiumonPrinciplesofdatabasesystems.ACM,2002： 1-16.

[4]ArtacM,JoganM,LeonardisA.IncrementalPCAforon-linevisuallearningandrecognition[C]//Proceedingsofthe16thInternationalConferenceonPatternRecognition.IEEE, 2002, 3: 781-784.

[5]LiY.Onincrementalandrobustsubspacelearning[J].Patternrecognition, 2004, 37(7): 1509-1518.

[6]RenCX,DaiDQ.Incrementallearningofbidirectionalprincipalcomponentsforfacerecognition[J].PatternRecognition, 2010, 43(1): 318-330.

[7]WengJ,ZhangY,HwangWS.Candidcovariance-freeincrementalprincipalcomponentanalysis[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2003, 25(8): 1034-1040.

[8]YanS,TangX.Largest-eigenvalue-theoryforincrementalprincipalcomponentanalysis[C]//Proceedingsofthe12thIEEEInternationalConferenceonImageProcessing(ICIP).IEEE, 2005, 1: 1181-1184.

[9]RossDA,LimJ,LinRS,etal.Incrementallearningforrobustvisualtracking[J].InternationalJournalofComputerVision, 2008, 77(1-3): 125-141.

[10]DuanG,ChenYW.Batch-incrementalprincipalcomponentanalysiswithexactmeanupdate[C]//Proceedingsofthe18thIEEEInternationalConferenceonImageProcessing(ICIP).IEEE, 2011: 1397-1400.

[11]JolliffeIT.PrincipalComponentAnalysis[M],secondeditioned.Springer, 2002.

[12]ChinTJ,SuterD.Incrementalkernelprincipalcomponentanalysis[J].IEEETransactionsonImageProcessing, 2007, 16(6): 1662-1674.

[13]YanJ,ZhangB,YanS,etal.Ascalablesupervisedalgorithmfordimensionalityreductiononstreamingdata[J].InformationSciences, 2006, 176(14): 2042-2065.

[14]YanJ,ZhangB,LiuN,etal.Effectiveandefficientdimensionalityreductionforlarge-scaleandstreamingdatapreprocessing[J].IEEETransactionsonKnowledgeandDataEngineering, 2006, 18(3): 320-333.

[15]YangY,LiuX.Are-examinationoftextcategorizationmethods[C]//Proceedingsofthe22ndannualinternationalACMSIGIRconferenceonResearchanddevelopmentininformationretrieval.ACM, 1999: 42-49.

[16]WittenIH,FrankE.DataMining:Practicalmachinelearningtoolsandtechniques[M].MorganKaufmann,SanFrancisco, 2005.

Centred Incremental Principal Component Analysis and Its Application in Text Classification

CHEN Sufen1, ZENG Xueqiang2

(1. School of Information Engineering, Nanchang Institute of Technology, Nanchang, Jiangxi 330099, China; 2. Computing Center of Nanchang University, Nanchang, Jiangxi 330031，China)

For the data mining of large-scale and streaming text data, incremental dimension reduction is an essential technique. As a state-of-the-art solution, Candid Covariance-free Incremental Principal Component Analysis (CCIPCA) applies an approximate centric alignment on the input data, where only the current sample is centred but all historical data are not updated properly. In this paper, we propose a Centred Incremental Principal Component Analysis (CIPCA) algorithm with exact historical mean update. Compared to CCIPCA, the proposed method not only correctly centered the current sample, but also correctly update all historical data by the current mean. The experiments on text streaming dataset show that CIPCA converges more quickly with the data flows in, and the performance improvement is especially obvious when the data’s inherent covariance is not stable.

principal component analysis; exact mean update; streaming data; dimension reduction; incremental learning