基于优化粒计算下微粒子动态搜索的K—medoids聚类算法

宋红海 颜宏文

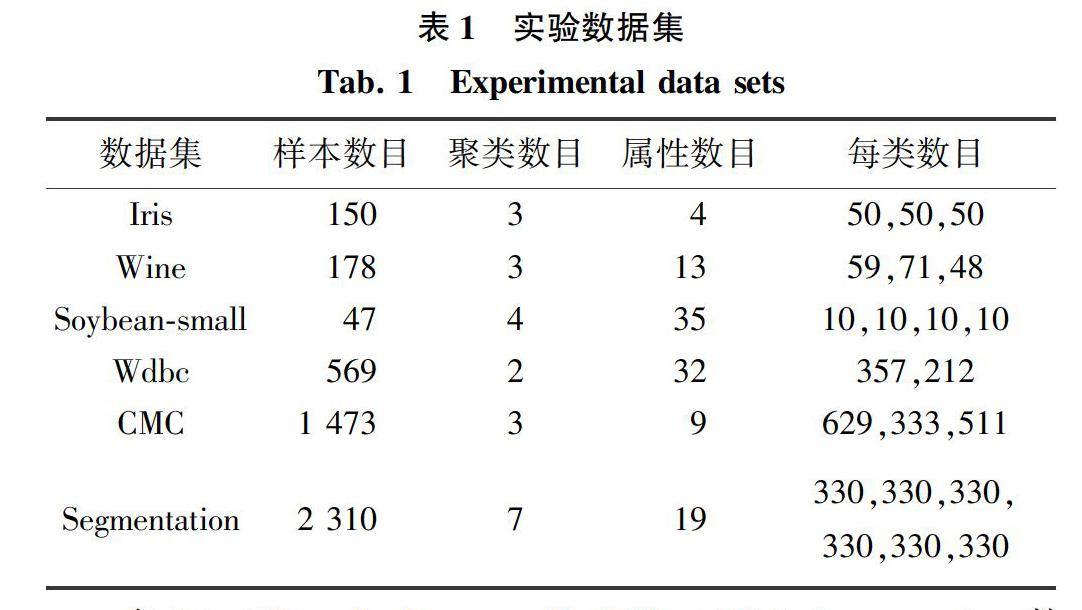
摘 要：K-medoids算法具有对初始聚类中心敏感，聚类准确度不高及时间复杂度大的缺点。基于此，文中提出一种优化的K-medoids算法；该算法在已有的粒计算初始化基础上进行了改进，以对象之间的相似性作为判断依据，结合最大最小法初始化聚类中心，能有效地获取最佳或近似最佳的聚类中心；在优化的粒计算前提下，提出了基于微粒子动态搜索策略，以初始中心点作为基点，粒子内所有对象到其中心的平均距离为半径，形成一个微粒子；在微粒子内部，采用离中心点先近后远的原则进行搜索，能有效地缩小搜索范围，提高聚类准确率。实验结果表明：在UCI多个标准数据集中测试，且与其他改进的K-medoids算法比较分析，该算法在有效缩短收敛时间的同时保证了算法聚类准确率。

关键字：聚类；K-medoids算法；粒计算；相似性；微粒子动态搜索

文献标志码： A 中图分类号：TP301.6文章编号：2095-2163（2016）02-

Novel K-medoids clustering algorithm based on dynamic search of Microparticlesunder optimizedgranular computing

SONG Honghai，YAN Hongwen

（ Institute of Computer and Communication Engineering， Changsha University of Sciences and Technology， Changsha Hunan 410114， China）

Abstract：The K-medoids algorithm has the disadvantage of sensitivity to cluster center initialization， low clustering accuracyand high the time complexity. So this paper proposes an optimized K-medoids algorithm； this algorithm has been initialized on the basis of granular computing which takes the similarity between objects as the basis to judge， and combined with the maximum and minimum cluster center initialization method the best or near-best cluster centercan be effectively accessed； Under the precondition of optimization of granular computing， the paper puts forward the dynamic search strategy based on the microparticles， the initial center as a base， all objects within the particles to an average distance of the center of the radius， form a microparticle； In microparticles inside， using the first after nearly far from the center of the principle of search， can effectively narrow the search， increase the clustering accuracy. Tested on a number of standard data sets in UCIand compared with other improved K-medoids algorithm， the experimental results show that this new algorithm reuduces the convergence time effectively and improves the accuracy of clustering.

Key word：clustering； K-medoids algorithm； granular computing；similarity； microparticles dynamic search

0 引言

聚类就是将拥有不同属性的事物划分成不同类的过程，不依赖于先验信息，只需考虑数据本身的特征属性以及数据间的相互关系[1]，同一类内的事物属性具有高质的相似性，不同类之间的属性则具有高度不相似性。作为一种重要的数据分析方法，聚类已经成为一种实用开发工具，广泛地应用到数据挖掘、模式识别、信息检索和图像处理等领域。

在时下经典的聚类算法中，K-medoids算法具有了较为普遍应用性。算法优点是实现思想简单，搜索能力强等，但也存在对初始化聚类中心敏感，时间复杂度较高，精确度不高等问题。针对这一特征状况，有大量学者提出了许多改进的算法：文献[2-4]提出了运用粒计算的思想来初始化 K-medoids 聚类中心，从而降低了时间复杂度，增强了局部搜索能力，但由于粒子多会表现出一定的随机性，使得准确率未获提高；文献[5]提出了一种改进粒计算的K-medoids算法，在相当程度上改善了K-medoids算法对初始化聚类中心敏感的问题，但因其搜索能力不强，导致精确度也未见可观增长；，进一步地，文献[6]则提出一个基于最小支撑树的初始化聚类中心方法，有效解决了初始化敏感的问题，但却增加了时间复杂度；另外，文献[7-8]又采用相异度矩阵来记录样本之间的距离，增强了局部搜索能力，同时降低了时间复杂度。

综上可知，各研究文献从不同方面对K-medoids算法实施了改进与优化，并已取得了一定的成果，但也存在明显的局限性，具体就是时间复杂度和准确度不能兼顾：有些以增加时间复杂度为代价来提高准确度，有些是以牺牲准确度来降低时间复杂度；还有一些则只是针对某种特定的数据。基于此，在现有粒计算的基础上，本文提出了一种基于优化粒计算初始化，微粒子动态搜索的K-medoids算法。

1 传统的K-medoids算法

K-medoids聚类算法根据K-means算法的思想改进而来[9]，是一种划分的方法，能够有效地处理异常数据和噪声数据，且具良好的鲁棒性。算法中采用欧氏距离来衡

基于粒计算初始化步骤如下：

3 算法的改进

3.1 粒计算的改进

基于粒计算初始化的步骤6改进如下：前2个初始化中心保持不变，仍然分别是粒子密度最大粒子的中心和距密度最大粒子最远且密度最大的粒子的中心，记为 和 ；对于剩下的粒子不是以欧氏距离作为依据，而是以对象间的相似度为依据，结合最大最小法，分别计算出剩余粒子的中心与 的相似度，记为 ，取 ，例如取第三个初始化中心时，分别计算出 ，则 ，依次类推，得到 个初始化聚类中心。

4.2基于微粒子动态搜索

基于改进的粒计算初 始化后，同一粒子中的对象具有高密度和高相似度，即同一粒子中的对象很大程度上可能属于同一簇，可以判定与初始化中心相近的对象是最优聚类中心的候选集。因此，提出一种基于微粒子动态搜索的策略。

3.2.1 新概念

粒子中对象到其中心的平均距离，对其数学定义可表述为：

其中， 是粒子 中对象 与中心 的欧氏距离， 是粒子 所包含对象的个数。

定义5 微粒子：以某一对象为基点，粒子中所有对象到粒子中心的平均距离为半径r，这样包含若干个对象的封闭区域。

3.2.2 微粒子搜索过程

以初始化中心 为基点，粒子 中所有对象 的平均距离 为半径，这样形成的圆区域内所包含的对象为一个微粒子；在微粒子内，以离初始化中心点 最近的对象作为新的聚类中心，根据准则函数可进行如下判断：

若新的准则函数 小于原准则函数 ，即 ，则用新的聚类中心点代替原中心点；再以新的聚类中心点为基点， 为半径，形成新的微粒子，在新的微粒子中应用上述搜索策略。

若新的准则函数 大于原准则函数 ，即 ，则中心点不变；采取先近后远的原则，以离初始化中心点 次近的对象作为新的聚类中心点，计算准则函数。

依此类推，直至找到最佳聚类中心。在粒计算有效初始化的前提下，基于微粒子动态搜索，缩小了寻找最佳聚类中心的范围，提高了搜索的效率。

改进算法的实现过程可具体描述如下：

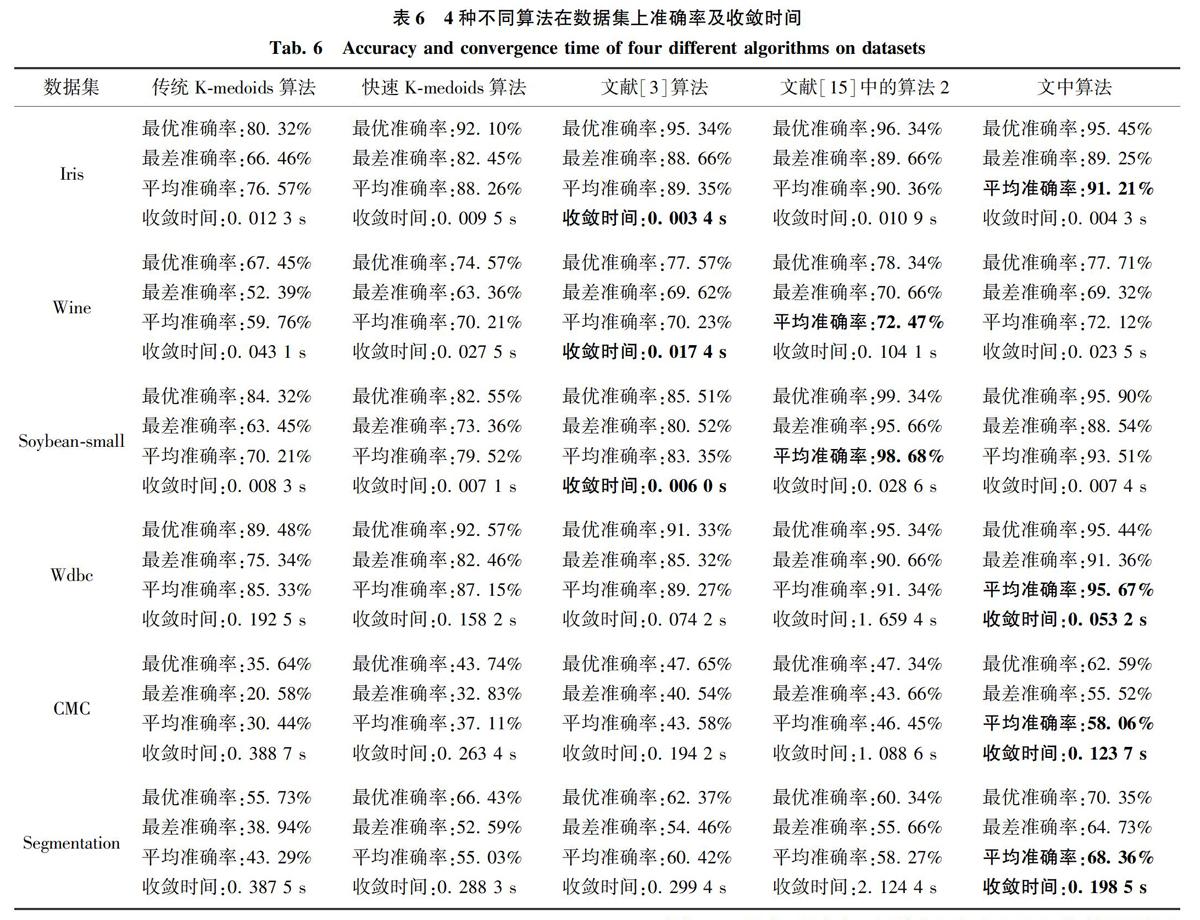
综上所述，实验从改进算法的准确率和收敛时间两个方面，与其他算法进行了对比。由实验可知文中算法能够收敛于最佳中心或最相似中心，提高了聚类的准确率和缩短了其运行的时间，尤其在相对较大的数据集上，文中算法的聚类效果明显优于其他算法。

5 结束语

K-medoids算法具有对初始聚类中心敏感，聚类准确度不高及时间复杂度大的缺点。文中提出了一种新的K-medoids算法，该算法采用改进的粒计算来克服K-medoids算法对初始化敏感问题，使用基于微粒子动态搜索策略改善了K-medoids算法全局搜索的能力，提高了算法精确度，同时也缩短了其收敛的时间。文中算法与其他改进的K-medoids算法作了对比，通过对比验证了文中算法的可行性与有效性。

参考文献：

[1]马儒宁，王秀丽，丁军娣.多层核心集凝聚算法[J].软件学报，2013，23（3）：490-506.

[2]王永贵，林琳，刘宪国.基于改进粒子群优化的文本聚类算法研究[J]计算机工程，2014，40（11）：172-177.

[3]马箐，谢英娟.基于粒计算的K-medoids 聚类算法[J].计算机应用，2012，32（7）：1973-1977.

[4]姚丽娟，罗可，孟颖.一种基于粒子群的聚类算法[J].计算机工程与应用，2012，48（13）：150-153.

[5]潘楚，罗可.基于改进粒计算的 K-medoids 聚类算法[J].计算机应用，2014，34（7）：1997-2000.

[6]李春生，王耀南.聚类中心初始化的新方法[J].控制理论与应用，2010，27（10）：1436-1440.

[7]陶新民，徐晶，杨立标等.一种改进的粒子群和 K均值混合聚类算法[J].电子与信息学报，2010，32（1）：93-97.

[8]HAE-SANG，PARK，CHI-HYUCKJ.Asimpleand fastalgorithmforK-medoidsclustering[J].ExpertSystems with Applications，2008，36（2）：3336-3341.

[9]Han Jiawei，Kamber M.数据挖掘：概念与技术[M].范明，译.北京：机械工业出版社，2012：293-297.

[10]张雪萍，龚康莉，赵广才.基于 MapReduce的 K-medoids并行算法[J].计算机应用，2013，33（4）：1024-1035.

[11]王国胤，张清华，胡军.粒计算研究综述[J].智能系统学报，2007，2（6）：8-26.

[12]王伦文.聚类的粒度分析[J].计算机工程与应用，2006，42（5） ：29-31.

[13]徐丽，丁世飞.粒度聚类算法研究[J].计算机科学，2011，38（8）：25-28.

[14]颜宏文，周雅梅，潘楚.基于宽度优先搜索的K-medoids聚类算法[J].计算机应用，2015，35（5）：1302-1305.

[15]谢英娟，鲁肖肖，屈亚楠等.粒计算优化初始聚类中心的K-medoids 聚类算法[J].计算机科学与探索，2015，9（5）：611-620.