一种传感网时间同步和定位的联合线性估计方法*

顾治华，朱雪芬，吴晓平，2*，陈道钱（.浙江农林大学信息工程学院，浙江临安3300；2.浙江省林业智能监测与信息技术研究重点实验室，浙江临安3300）



一种传感网时间同步和定位的联合线性估计方法*

顾治华1，朱雪芬1，吴晓平1，2*，陈道钱1
（1.浙江农林大学信息工程学院，浙江临安311300；2.浙江省林业智能监测与信息技术研究重点实验室，浙江临安311300）

摘要：采用时间测量以估计节点位置的方法实现简单，在传感网中得到了广泛的使用。然而节点计时时钟存在漂移和偏离，导致时间测量不准确。为此文本以节点时钟漂移和偏离模型为基础，提出了一种时间同步和节点定位的联合线性估计方法，包括最小平方（LS）及权重最小平方（WLS）方法。仿真测试了所设计算法的运行时间，分析了噪声对联合估计方法的估计误差影响。结果表明，LS及WLS线性估计方法运算速度较半正定（SDP）算法快，在低噪声条件下LS及WLS线性估计方法具有较高的稳定性和定位精度。

关键词：传感网；定位；时间同步；到达时间

项目来源：国家自然科学基金项目（61190114，61303236）；浙江省自然科学基金项目（LY16F020036）；浙江农林大学人才启动项目（2013FR086）；浙江省科技计划项目重大科技专项项目（2012C13011-1）

无线传感器网络（简称传感网）是通过将大量具有传感器单元、数据处理单元及通信模块的微小智能节点密集地散布在感知区域，节点间以自组织方式构成的无线通信网络。节点传感信息的采集在大多数情况下都与节点所处的地理位置相联系才有意义，因此国内外的众多专家学者已经开展了很多无线传感器网络定位方面的研究［1-2］。根据节点在定位过程中是否需要直接测距，可将定位方法分为非测距和测距的定位方法。非测距定位方法以节点间连通性、网络拓扑结构估计节点间距离，并以此来定位未知节点。但由于非测距方法的节点间距离估计误差较大，定位精度也较低，在定位精度要求较高的场合下难以适用。测距定位方法依赖于节点间精准的测量距离，常用的测量距离方法包括到达时间（TOA）［3-4］、到达时间差（TDOA）［5］、无线信号接收强度（RSS）［6-7］及能量强度［8］等。由于TOA测距方法实现原理较简单，成本低，在众多的定位系统中都得到了广泛的应用。

已有大量关于传感网的定位算法，如极大似然（ML）估计［8］、线性代数估计法［9］及凸优化［10-12］等实现方法。ML估计方法在弱噪声范围内，具有较好的定位精度。但其数值计算方法依赖于初始解的选择，若初始解选择不合适，有可能陷入局部最优，为此提出了凸优化及线性代数法等其它方法。凸优化方法包括半正定（SDP）［10- 11］和二阶锥规划（SOCP）［12］将优化模型松弛为凸优化问题，是当前传感网定位方法中比较流行的一种方法。凸优化方法的求解不依赖于初始化过程，但由于凸优化函数中具有较多的变量和等式约束，计算复杂度较高。为降低计算复杂度，线性代数法将计算结果直接表示为代数解，避免了初始解的选择问题，计算过程也较快，但对强噪声环境下的抗干扰能力较弱。

采用TOA建立节点间距离约束关系以估计节点位置坐标的方法与时间测量有关。然而由于初始化或环境因素变化有可能导致节点计时时钟失步，导致测量时间的不准确，为此提出了时间同步和定位的联合计算方法。如文献［13］采用多个天线接收器，提出了节点时钟偏离和目标位置的联合估计方法，实现了时间同步和定位的联合计算。考虑节点的时钟漂移的偏离模型，一种期望最大化（EM）方法［14］被设计用来联合估计时钟同步参数及未知节点位置坐标。假设所有信标节点的时钟是同步的，而未知节点存在时钟漂移和偏离，文献［15］提出了基于SDP方法的未知节点的目标位置以及时间同步的联合代数计算方法。

本文首先根据节点间来回信号传递的计时时钟模型，推导了观测时间与实际时间的关系，并以此建立了时间同步和定位的联合估计方程。以节点时钟漂移和偏离模型为基础，提出了一种时间同步和节点定位的联合线性估计方法，实现节点时钟漂移率、偏离量和位置坐标的同时估计。本文第1部分首先介绍了定位及时间同步问题描述；第2部分建立了时间同步和定位的联合估计方程；第3部分详细推导了联合线性估计方法的实现过程；第4部分为仿真与分析；最后部分为结论。

1　问题描述

假设在二维坐标平面上分布着M个未知位置坐标的节点（简称为未知节点），其位置坐标分别为xi=[xiyi]T，（i=1,2,̌,M）。同时在该区域内存在N个已知位置坐标的信标节点，其位置坐标分别为xj=[xjyj]T，(j=M+1,M+2,̌,M+N)。为估计未知节点位置坐标，未知节点i与信标节点j间测量信号到达时间（TOA）以建立距离约束关系。然而由于节点所处环境参数、初始化等原因使得节点计时时钟失步，引起节点观测时间与实际时间不一致。若直接使用观测时间估计未知节点位置坐标，将会使节点位置坐标估计发生严重错误。

无线传感器网络节点时钟失步的主要原因来自三个方面：①温度、压力、电源电压等环境因素的变化导致的节点时钟漂移；②为节省能耗，节点不断切换工作状态，频繁初始化导致时钟初始值存在差异；③特殊事件处理对时钟的影响，如时钟中断引起的时钟误差。综合上述三个因素，本文采用漂移和偏离的时钟计时模型，建立观测时间与实际时间的相互关系。假设ωi为时钟漂移率，表示了节点i上观测时间与实际时间的时间变化率，θi为时钟偏离量，表示了观测时间与实际时间在同一时刻的时间差。将节点i的观测时间Ti与实际时间t表示为以下关系式

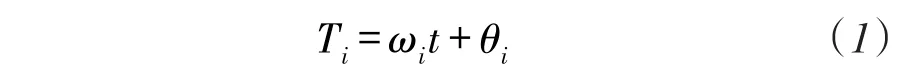
2　时间同步和定位的联合估计方程

图1绘出了未知节点i与信标节点j间的TOA测量时间与实际时间的关系。未知节点i在Ti,j时刻（Ti,j为节点i时钟的观测时间）发送信号给信标节点j，节点j在Ri,j时刻（Ri,j为节点j时钟的观测时间）收到节点i的信号，根据式（1）有以下关系式

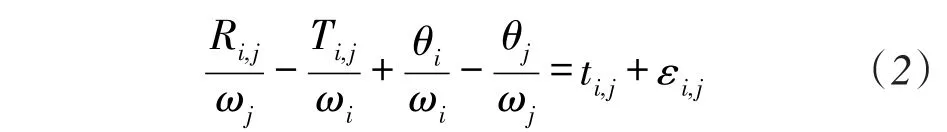
式中，ti,j为节点间信号到达时间，ti,j=di,j/c，di,j为节点间距离，c为信号传播速度，如电磁波传播速度c=3×108m/s。εi,j表示了未知节点i与信标节点j间的时间测量噪声，可以假设εi,j服从均值为零，方差为δ2i,j的高斯分布。

当信标节点j收到未知节点i的信号之后，节点j又在Ťi,j时刻（Ťi,j为节点j时钟的观测时间）发送信号给节点i，节点i在Ři,j时刻（Ři,j为节点i时钟的观测时间），同式（2）的类似推导过程，有

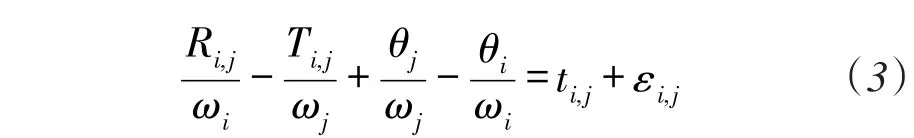
式中，ti,j的定义同式（2），ε̌i,j亦为噪声部分，假设ε̌i,j服从均值为零，方差为δ̌2i,j的高斯分布。

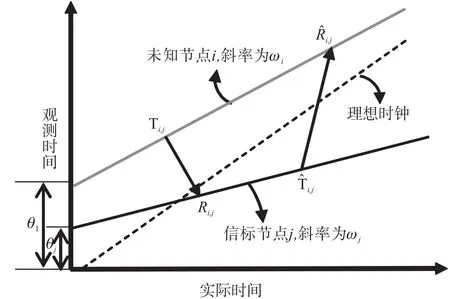
图1　TOA的测量时间与实际时间关系

为了联合估计时间同步参数和节点位置坐标，本模型假设未知节点的时钟参数是经过校准的，即时钟参数ωi、θi（i=1,2,̌,M）及信标节点的位置坐标xj(j=M+1,M+2,̌,M+N)为已知值，而信标节点时钟同步参数包括漂移率ωj、偏移量θj(j=M+1,M+2,̌,M+N)为未知参数，即通过ωi、θi(i=1,2,̌,M)与xj(j=M+1,M+2,̌,M+N)联合估计未知参数xi(i=1,2,̌,M)及ωj、θj(j= M+1,M+2,̌,M+N)。

3　联合线性估计方法

3.1估计方法推导过程

将式（2）及（3）相加，可消去公共项，有

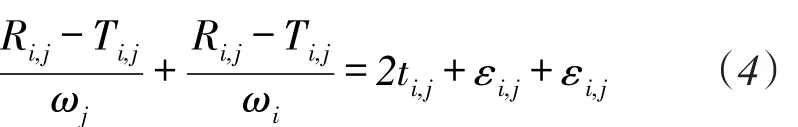
由于ωj非常接近于1，可假设ωj=，δj为接近于零的变量，j=M+1,M+2,̌,M+N。故式（4）可以改写为

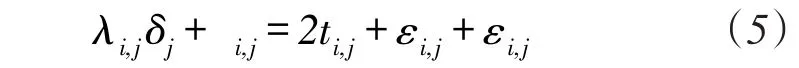
式（5）中，i,j=Ri,j-Ťi,j+，λi,j=Ri,j-Ťi,j。由于ti,j=且di,j=，对式（5）两边平方，忽略二次高阶项，经整理有表达式

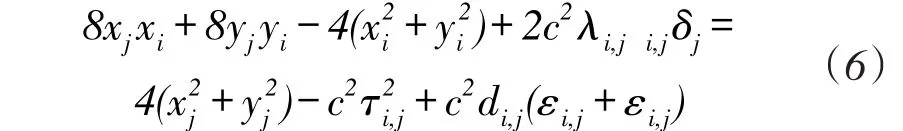
式（6）中，i=1,2,̌,M，j=M+1,M+2,̌,M+N。令，依照i、j从小到大的顺序，将所有节点间的连接表达式（6）写成矩阵形式

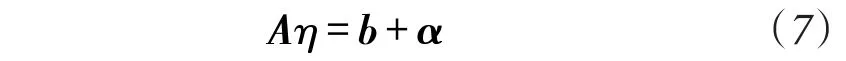
由式（6）判断，式（7）中矩阵A的行向量值为[01×3(i-1)8xj8yj-4 01×3(M-i)+j-12c2λi,jτi,j01×(N-j)]， b及噪声α的行元素值为， [c2di,j(εi,j+ε̌i,j)]。假设M个未知节点与N个信标节点间共存在L个时间测量连接，则有A∈RL×(3M+N)，b∈RL×1，α∈RL×1。

根据线性最小二乘法原理，未知参数η的无偏估计值为

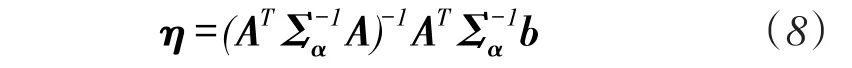
式中维度为L×L的矩阵Σα=E(αTα)，其值为

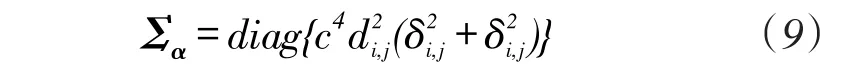
式中，di,j为未知参数，可预先设置Σα为单位矩阵，以式（8）近似估计未知节点位置坐标，此算法的所有测量连接的权重值都相等，称为最小平方（LS）算法。然后以LS算法的近似估计值计算di,j，再以式（9）重新计算Σα及η，将此过程称之为权重最小平方（WLS）算法。根据参数η的定义，可从估计值η提取出未知节点位置坐标及信标节点的时间漂移率，

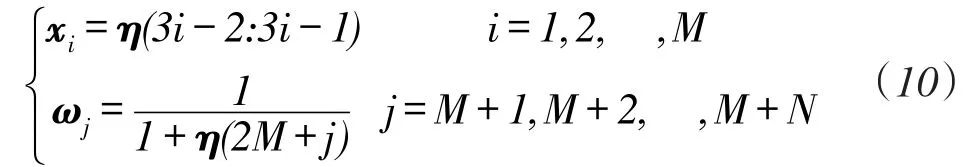
式（10）计算出了未知节点位置坐标估计值xi及信标节点的时钟漂移率ωj。为完整地表述时间同步参数，下面推导偏移量θj参数估计过程。将式（2）减去式（3），有以下表达式

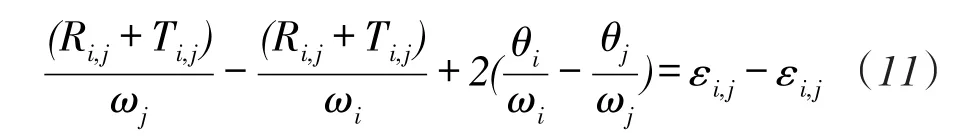
由ωj=，忽略误差项，由式（11）得到

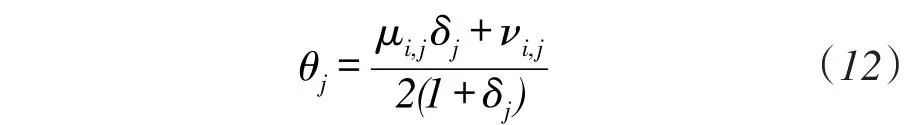
式中，νi,j=Ri,j+Ťi,j-，μi,j=Ri,j+Ťi,j， j=M+1,M+2,̌,M+N，再次依照i、j从小到大的顺序，将所有节点间的连接表达式（12）写成矩阵形式

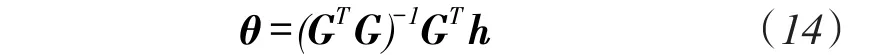
3.2算法实现流程

①根据矩阵A、向量b的定义，表示出A、b的值，A∈RL×(3M+N)，b∈RL×1。

②预先设置Σα为单位矩阵，以式（8）近似估计未知节点位置坐标，得到LS算法的估计结果。

③以LS算法的估计值近似计算出di,j及Σα，再根据WLS算法，由式（8）再次估计向量η。

④从η中提取出未知节点位置坐标的估计值xi及信标的时间漂移率ωj。

⑤根据矩阵G、向量h的定义，表示出G、h的值，G∈RL×(2M+N)，h∈RL×1。

⑥由式（14）估计信标节点的时间偏移量θ。

4　仿真分析

假设所有未知节点是时间同步而信标节点存在时间漂移，本文提出了一种时间同步和定位的联合线性估计方法。为验证所设计算法的性能，将所提出的算法与文献［15］所提出的SDP算法进行了运行时间、估计精度两方面的比较。文中所提出的联合线性估计方法及SDP算法均采用MATLAB软件进行了仿真，且凸优化SDP算法采用CVX工具箱下的SeDuMi求解器计算。

4.1算法的平均运行时间

在20 m×20 m的二维区域平面上，预先将五个信标节点位置分别设置在（0，0），（0，20），（20，0），（20，20），（10，10）点，并随机生成M个未知节点。假设未知节点与每个信标节点间的时间测量噪声εi,j、ε̌i,j都服从均值为0，方差为δ2的高斯分布。假设所有未知节点与信标节点间都存在测量连接，分别设置未知节点数量M=6,7,8,9,10，表1列出了1 000次蒙特卡罗（MC）下LS、WLS和SDP算法的单次平均运行时间。随着未知节点数量M的上升，节点间存在的测量连接数量增加，三种算法的平均运行时间都随之增加。由于WLS需要再次计算权重值，故WLS算法的运行时间几乎比LS算法增加一倍。相比于凸优化的SDP算法，LS及WLS算法的运行时间缩减了很多。如当M=10时，SDP算法的平均运行时间为620.3 ms，而LS及WLS算法的平均运行时间仅为3.3 ms、6.4 ms。

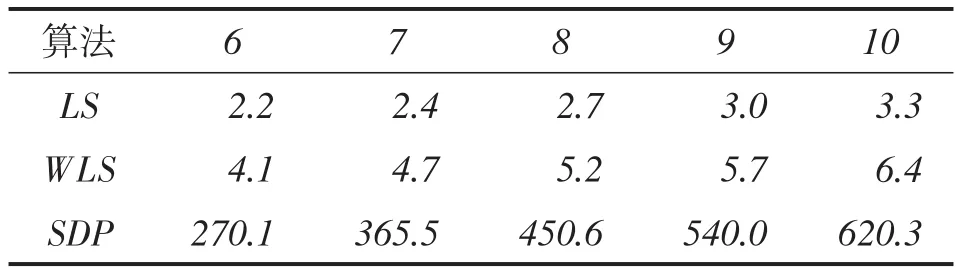
表1　不同算法的单次平均运行时间比较　单位：ms

4.2定位误差比较

众所周知，由于进行了凸优化松弛，SDP算法的定位结果非最优。而本文所提出的线性估计方法假设zi中各参数相互独立，亦降低了定位精度。为验证本文所提出的LS、WLS算法的估计误差，将算法的定位精度同文献［15］的SDP算法及克拉美罗下界（CRLB）［15］进行了比较。相同于4.1中信标节点的坐标位置设置，随机生成的十个未知节点分别设置在如图2所示的位置分布。

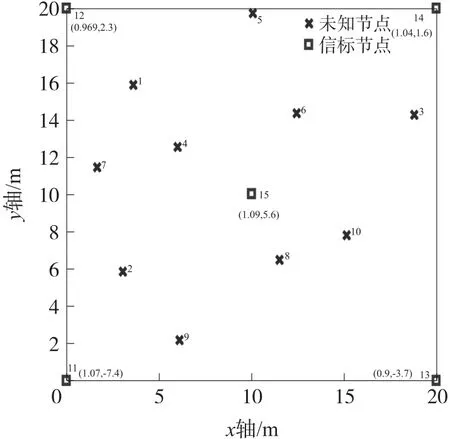
图2　未知节点与信标节点的位置分布

假设所有未知节点是时钟同步的，即ωi=1，θi=0，i=1,2,̌,10，将信标节点的时钟漂移率及偏移量标记为(ωj,θj)，j=11,12,̌,15，具体值如图2标注所示。假设信号传播速度c=3×108m/s，未知节点与信标节点的时间测量噪声εi,j、ε̌i,j以纳秒为单位，且都服从均值为0，方差为δ2的高斯分布。为评价该LS、WLS、SDP三种算法下的定位精度，采用均方根误差（RMSE）分析。对每种算法下的RMSE定位误差仿真运行1 000次，采用1 000次运行的平均值进行对比分析。

取十个未知节点的平均RMSE分析其定位精度性能，图3绘出了LS、WLS、SDP算法的平均RMSE定位误差比较。由图3可见，当噪声大小δ 从0.2增加到2时，三种算法的RMSE定位误差都随之增大。在低噪声条件（δ≤1.2）时，SDP算法的定位误差在3种算法中最大。但是当噪声δ大于1.2之后，SDP算法的定位误差小于LS算法，但仍大于WLS算法。同时也可以看出定位误差RMSE值与噪声δ之间有近似的线性关系，定位误差随着噪声的增加而增大。当噪声δ为0.2时，WLS算法的RMSE值为0.05 m；而当噪声δ等于2时，WLS算法的RMSE值增加到了0.52 m。

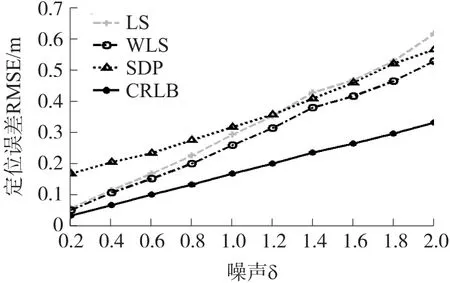
图3　定位误差随噪声大小变化关系

4.3时间同步参数估计误差

信标节点的时间同步参数包括时钟漂移率、偏离量与未知节点的位置坐标同时被估计。取五个信标节点的平均时钟漂移率、偏离量分析其估计误差，其结果绘在图4中。

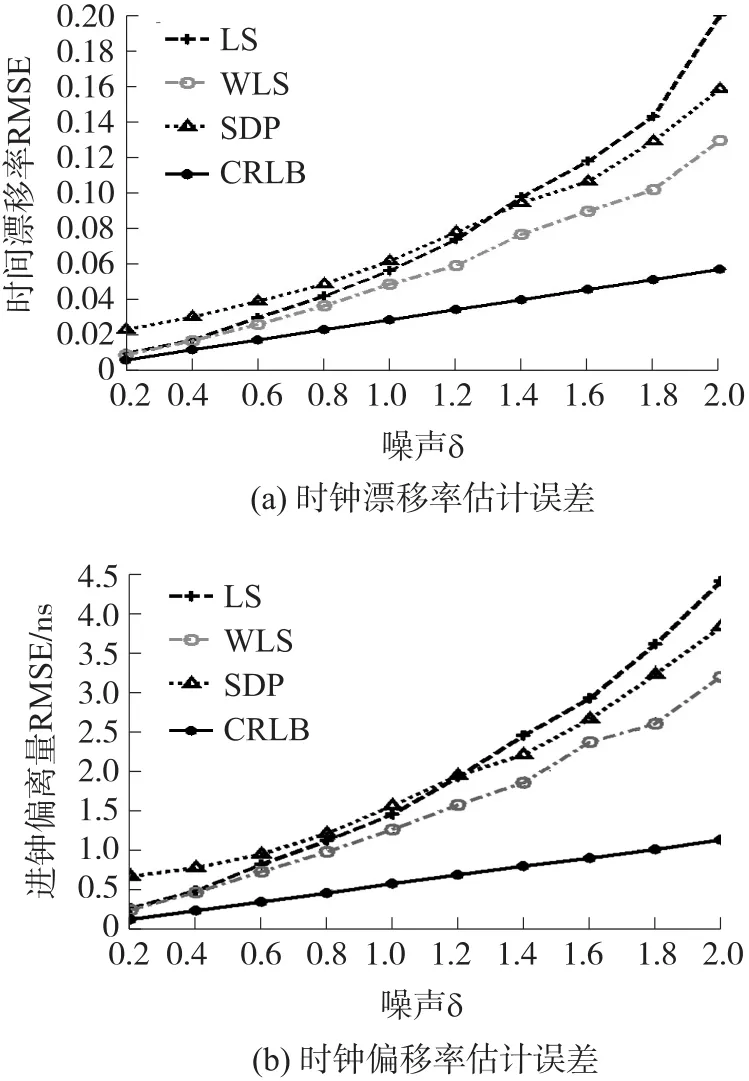
图4　时间同步参数的估计误差分析

观察图4（a）及图4（b）的时钟漂移率及偏离量随噪声δ的变化曲线，不难发现，算法的变化规律类似图3所反映的结果。当δ≤1.2时，SDP算法的估计误差较LS及WLS算法的估计误差大；而δ>1.2时，LS算法的估计误差较SDP算法大。相对于LS及WLS线性估计方法，凸优化的SDP算法随噪声的变化较为平缓。如当δ为0.2时，SDP算法的时钟漂移率RMSE为0.02，而LS及WLS算法的时钟漂移率RMSE仅为0.01；而当噪声δ等于2时，SDP算法的时钟漂移率RMSE增加到了0.16，LS及WLS算法的时钟漂移率RMSE分别增加到了0.20及0.13。

同样地，时钟偏离量估计误差也有类似上述规律。当噪声δ≤1.2时，LS及WLS的估计误差比SDP算法的估计误差小；当δ>1.2时，LS算法的估计误差较SDP算法大，但WLS算法的估计误差仍是最小的。算法的估计误差与噪声大小近似有线性关系，当噪声δ为0.2时，WLS算法的时钟偏离量RMSE值为0.24 ns；而当噪声δ增大到2时，WLS算法的时钟偏离量RMSE值也增加到了3.2 ns。

5　结论

本文介绍了一种无线传感器网络的时间同步和定位联合线性估计方法。该方法针对时钟漂移和偏离的TOA测距定位模型，将时间同步参数和节点位置坐标同时估计出来，即实现了时间同步，又实现了节点位置坐标估计。与凸优化SDP方法相比较，所设计的LS、WLS线性估计方法计算复杂度低，运算速度快；在低噪声条件下，其估计误差较小。但本文所提出的LS、WLS线性方法的估计误差并未达到CRLB下界值，其结果还有待于进一步通过优化方法求精。

参考文献：

［1］Liu Yunhao，Yang Zheng，Wang Xiaoping. Location，Localization，and Localizability［J］. Journal of Computer Science and Technolo⁃gy，2010，25（2）：274-297.

［2］叶苗，王宇平.一种新的容忍恶意节点攻击的无线传感器网络安全定位方法［J］.计算机学报，2013，36（3）：532-544.

［3］Wang Yuan，Ma Shaodan，Philip C L Chen. TOA-based Passive Localization in Quasi-Synchronous Networks［J］. IEEE Communi⁃cations Letters，2014，18（4）：592-595.

［4］Shen Hong，Ding Zhi，Dasgupta Soura，et al. Multiple Source Lo⁃calization in Wireless Sensor Networks Based on Time of Arrival Measurement［J］. IEEE Transactions on Signal Processing，2014，62（8）：1938-1949.

［5］Yang Le，Ho K C. An Approximately Efficient TDOA Localization Algorithm in Closed-form for Locating Multiple Disjoint Sources With Erroneous Sensor Positions［J］. IEEE Transactions on Signal Processing，2009，57（12）：4598-4615.

［6］袁鑫，吴晓平，王国英.线性最小二乘法的RSSI定位精确计算方法［J］.传感技术学报，2014，27（10）：1412-1417.

［7］Xu Yaming，Zhou Jianguo，Zhang Peng. RSS-based Source Local⁃ization When Path-loss Model Parameters are Unknown［J］. IEEECommunications Letters，2014，18（6）：1055-1058.

［8］Sheng Xiaohong，Hu Yuhen. Maximum Likelihood Multiplesource Localization Using Acoustic Energy Measurements with Wireless Sensor Networks［J］. IEEE Transactions on Signal Pro⁃cessing，2005：53（1）：44-53.

［9］So H C，Lin Lanxin. Linear Least Squares Approach for Accurate Received Signal Strength Based Source Localization［J］. IEEE Transactions on Signal Processing，2011，59（8）：4035-4040.

［10］Biswas Pratik，Liang Tzu-Chen，Toh Kim-Chuan，et al. Semidefi⁃nite Programming Approaches for Sensor Network Localization with Noisy Distance Measurements［J］. IEEE Transactions on Au⁃tomation Science and Engineering，2006，3（4）：1-11.

［11］吴晓平，谈士力.基于半定规划的无线传感器网络定位算法性能分析［J］.传感技术学报，2012，25（12）：1731-1736.［12］Ghasem Naddafzadeh- Shirazi，Michael Botros Shenouda，Lutz Lampe. Second Order Cone Programming for Sensor Network Lo⁃calization with Anchor Position Uncertainty［J］. IEEE Transac⁃tions on Wireless Communication，2014，13（2）：949-963.

［13］Yousefi Siamak，Chang Xiaowen，Champagne Benoit. A Joint Lo⁃calization and Synchronization Technique Using Time of Arrival at Multiple Antenna Receivers［C］. 2013 Asilomar Conference on Signals，Systems and Computers，2013：2017-2021.

［14］Aitzaz Ahmad，Erchin Serpedin，Hazem Nounou，et al. Joint Node Localization and Time-Varying Clock Synchronization in Wireless Sensor Networks［J］. IEEE Transactions on Wireless Communica⁃tion，2013，12（10）：5322-5333.

［15］Reza Monir Vaghefi，R. Michael Buehrer. Cooperative Joint Syn⁃chronization and Localization in Wireless Sensor Networks［J］. IEEE Transactions on Signal Processing，2015，63（14）：4035-4040.

顾治华（1991-），女，甘肃兰州人，硕士研究生，研究方向为无线传感器网络资源优化与定位计算，guzhihuayiran@163.com；

吴晓平（1977-），男，浙江金华人，副教授，博士，硕士研究生导师，研究方向为无线传感器网络与分布式计算。在国内外重要会议及期刊上发表论文二十多篇，其中SCI收录6篇，wuxipu@gmail.com。

A Joint Linear Estimation Approach for Time Synchronization
and Localization in Wireless Sensor Networks*

GU Zhihua1，ZHU Xuefeng1，WU Xiaoping1，2*，CHEN Daoqian1
（1.School of Information Engineering，Zhejiang A& F University，Lin’an Zhejiang 311300，China；2.Zhejiang Provincial Key Laboratory of Forestry Intelligent Monitoring and Information Technology，Lin’an Zhejiang 311300，China）

Abstract：It is simple to estimate the locations of sensor nodes by using the time measurements which are widely used in sensor networks. However there is a drift and deviation of the time clock，which leads to inaccurate time measurement. Based on the clock drift and deviation model，a joint linear estimation method for time synchroniza⁃tion and node localization is proposed，including the least squares（LS）and the weighted least squares（WLS）meth⁃od. The simulations tested the running time of the designed algorithm and analyzed the impacts of the noises on the estimation error with the joint estimation method. The results show that the LS and WLS linear estimation algo⁃rithms run faster than the SDP algorithm，and the LS and WLS linear estimation methods have high stability and ac⁃curacy in low noise conditions.

Key words：wireless sensor networks；localization；time synchronization；time of arrival（TOA）

doi：EEACC：6150；7110；521010.3969/j.issn.1004-1699.2016.03.016

收稿日期：2015-10-07修改日期：2015-12-10

中图分类号：TP393.0

文献标识码：A

文章编号：1004-1699（2016）03-0397-06