基于柔性铰链的杠杆-平衡机构的运动特性分析与参数设计*
2016-05-03刘庆纲秦自瑞郎垚璞天津大学精密测试技术及仪器国家重点实验室天津300072
刘庆纲,孙 庚,秦自瑞,郎垚璞(天津大学精密测试技术及仪器国家重点实验室 天津 300072)
基于柔性铰链的杠杆-平衡机构的运动特性分析与参数设计*
刘庆纲*,孙庚,秦自瑞,郎垚璞
(天津大学精密测试技术及仪器国家重点实验室天津300072)
摘要:基于微小力测量(mN级分辨力,N级测量范围)的柔性铰链杠杆-平衡机构,建立了此机构的运动数学模型,并利用有限元方法对该数学模型进行了验证。数学模型计算及有限元分析结果表明,减小柔性铰链的刚度、增大平行四杆机构的长度能增大被测力产生的位移,通过合理地选择铰链支点两侧的杠杆长度,能设计出所需的杠杆比及运动模型,从而为该机构的设计提供了理论依据。
关键词:杠杆平衡机构;运动特性;ANSYS FEM分析;柔性铰链
项目来源:国家自然基金项目(51575387);教育部博士点基金项目(20120032110059);天津市自然基金重点项目(14JCZDJC31100)
力平衡法是实现精密力测量的一种常用方法[1-2],该原理为被测力与作为测量系统的特定机构所施加的力经平衡机构平衡,通过测量施加力得到被测力的大小,而设计高精度的平衡机构,是实现被测力高精度测量的关键[3]。
柔性铰链是一种小体积、无机械摩擦、无间隙和运动灵敏度高等特点的传动机构,是为实现小范围的偏转和定位而提出的一种机构,因此被广泛应用在各种精密机构的设计中[4-7]。应用柔性铰链设计精密力测量设备的平衡机构是实现高精度力测量的一种常用方法,如梅特勒-托莱多有限公司生产的高精度电子天平即采用基于柔性铰链设计的平衡机构,但未见到该机构的数学运动模型;国内也有厂家及高校对该结构进行研究,如湖南大学的邵万里等人应用簧片替代柔性铰链设计平衡机构[8-9],并对该机构的挠度进行了研究,但也未对该机构的数学运动模型进行解析;张霖[10]等人用材料力学能量法对平行四杆柔性铰链机构的运动模型进行了推导,并用有限元方法对数学模型的正确性进行了验证,但同样没有建立测力的一体化杠杆放大-平衡机构的数学模型。由于平行四杆柔性铰链机构为杠杆-平衡机构的一部分,相比于平行四杆柔性铰链机构,杠杆-平衡机构提供了力及位移的杠杆放大比,同样的被测力易于产生更大的位移,在测力机构中具有不可替代的作用。因此,建立一体化柔性铰链杠杆-平衡机构的数学运动模型并对杠杆-平衡机构的运动模型进行力学及结构分析,是此类微力测量力学模型中亟待解决的问题。
本文以柔性铰链平衡机构为研究对象,从一体化柔性铰链杠杆-平衡机构的基本结构出发,利用材料力学能量法对该机构的运动进行数学分析,建立该机构运动的数学运动模型,利用有限元方法对该机构的数学运动模型进行验证,并根据数学模型及有限元分析结果分析该机构各个参数在设计时的选取方法,为一体化柔性铰链杠杆-平衡机构的设计提供理论依据。
1 一般柔性铰链的运动特性
目前,常见的柔性铰链结构形式主要有三种,正圆形、椭圆形和直角形[11]。不同类型柔性铰链的转动刚度、转角偏移量和灵敏度等均有所不同,其中正圆形柔性铰链具有运动精度较高、易加工等特点,所以应用范围较广。
正圆形单轴柔性铰链的结构参数如图1所示。图中R为柔性铰链的切割半径,t为铰链的最小厚度,b为柔性铰链的宽度,E为柔性铰链材料的杨氏模量,组成柔性铰链主要基本形变的是绕Z轴的力矩作用下产生的转动,柔性铰链绕Z轴的转动刚度K的性能参数计算公式如下[12-13]:
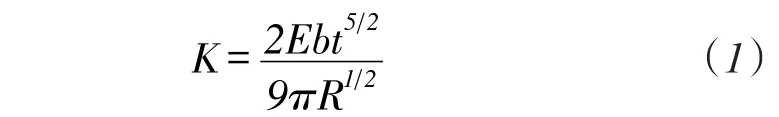
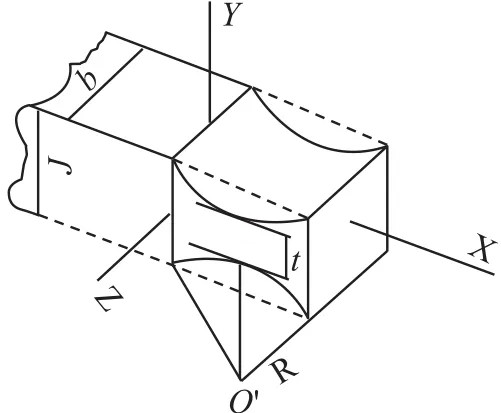
图1 正圆形柔性铰链结构
2 基于柔性铰链的杠杆-平衡机构
目前,被广泛应用的基于柔性铰链的平行四杆柔性铰链机构如图2所示,A、A′、B、B′、C、C′、D、D′分别代表相应的柔性铰链。图2为基于柔性铰链的杠杆-平衡机构,由A、A′、B、B′、C、C′、D、D′、E、F、G的柔性铰链及相应铰链间刚体构成,其中A、A′、B、B′、C、C′、D、D′柔性铰链及相应刚体所构成如图3所示的平行四杆柔性铰链机构,用于消除被测力的四角误差,防止被测力由于施力点偏置所造成的误差;柔性铰链G及两侧刚体构成如图4所示的杠杆机构,该机构为被测力和所施加力之间提供杠杆;柔性铰链E、F及之间的刚体构成如图5所示的拉带机构,该机构为杠杆机构和平行四杆柔性铰链机构之间提供柔性和位移转移作用。为简化起见,图2、图3中连接C、C′、D、D′的刚体约束并未画出。
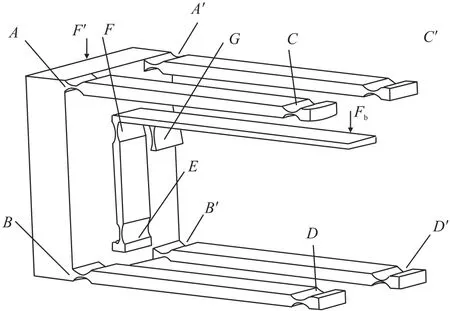
图2 基于柔性铰链的平衡机构
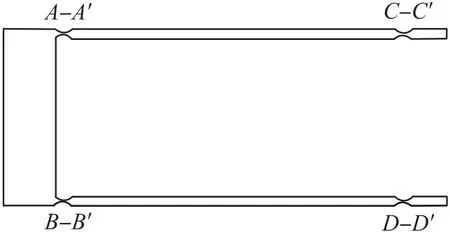
图3 柔性铰链平行四杆机构

图4 杠杆机构

图5 拉带机构
机构的作用原理如图6所示,施加被测力F′后,平行四杆柔性铰链机构产生垂直向下的位移,该位移带动柔性铰链拉带机构向下移动,将位移传递到柔性铰链杠杆机构,使柔性铰链杠杆机构绕支点铰链G转动,此时设置在杠杆另一端的位移检测机构在右端产生位移时检测出被测信号,并在该侧由力发生机构施加如图2所示的电磁平衡力Fb,使该杠杆重新稳定到最初的位置,此时通过右端施加的电磁平衡力Fb的大小即可通过杠杆比得出被测力的大小[14]。
在设计该类平衡机构时,为了满足测量分辨力的要求,设计所需要考虑的必要条件为被测最小力应使杠杆右端产生的位移能被位移检测机构检测。杠杆的位移放大比由于涉及到平衡力Fb与被测力的比值,因此也是设计时应考虑的因素。
3 柔性铰链平衡机构的运动及位移计算公式
基于材料力学能量法,对柔性铰链杠杆-平衡机构的右端位移分析如下:
平行四杆柔性铰链机构的运动模型[9]中,杠杆机构及其左端铰链F的受力运动特性为:拉带机构在柔性铰链平行四杆机构受力向下运动后,铰链F向下移动带动杠杆倾斜,从而带动铰链G转动,由于杠杆为一刚体,因此,铰链F和铰链G在同一方向上有相同的转动角度,杠杆右端通过铰链G的转动产生位移。拉带机构的运动特性为杠杆机构和平行四杆柔性机构之间的运动提供柔性,消除平行四杆柔性机构的耦合位移[15],防止由于耦合位移的影响造成柔性铰链在运动过程中的扭曲变形。其整体的运动特性原理图如图6所示。
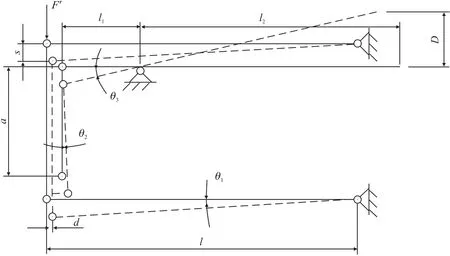
图6 运动特性原理图
在被测力F′作用下,左端刚体产生沿F′方向的位移S,由于该机构在设计时通常被用于微小力的测量,因此,位移S在实际应用中往往远小于l等参数。此时,根据柔性铰链平行四杆机构的运动特性,柔性铰链平行四杆机构的4个铰链的旋转角度为:θ1=s/l,耦合位移为:d=s2/2l,铰链F的耦合位移为d′=s2/l1,拉带结构用于消除耦合位移,因此,拉带结构的铰链E的转动角度为:θ2=arcsin((d-d′)/a)= (d-d′)/a;由于在实际设计中应尽力减小耦合位移,故a的长度往往设计得尽可能大,l和a的长度通常远远大于s,因此θ2的值往往比θ1小几个数量级,可忽略不计。平衡杠杆的支点铰链和左端的铰链的转动角度可由运动原理图得出为:θ3=arcsin(s/l1)= s/l1。
为便于计算,根据材料力学能量法[15-16],设该平衡杠杆机构在力F′处的刚度为Kt,平行四杆机构的八个铰链的转动刚度均为K1,拉带机构的两个铰链的转动刚度均为K2,杠杆的支点铰链的转动刚度为K3。由于θ2远小于θ1和θ3,则有:
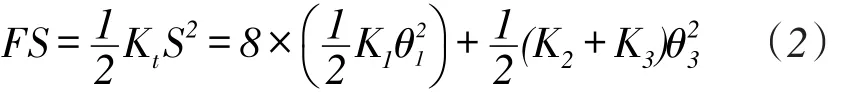
将θ1和θ3的值代入式(2),可得Kt为:
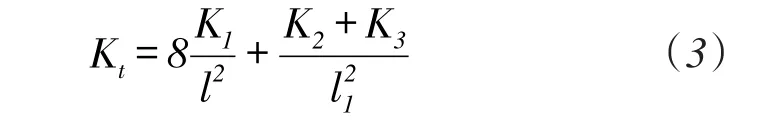
则在力F′的作用下,位移S为:

则杠杆右端位移为:

将式(3)和式(4)代入式(5)中可得右端位移与力F’及该机构各参数的关系式为:

4 有限元验证及设计分析
采用有限元分析软件ANSYS12.0建立柔性铰链平衡机构的有限元模型,在图2中的柔性铰链平行四杆机构的C、C′、D、D′铰链的右侧刚体及支点铰链G的下部进行全约束,施加外力F=1×10-5N,从而可得出柔性机构的位移S。有限元单元类型为Solid95,采用六面体单元划分网络,参照常用的该机构尺寸及材料,机构的材料选用航空铝,弹性模量E=71 GPa,泊松比μ=0.33,定义A、A′、B、B′、C、C′、D、D′柔性铰链为最小厚度t1=0.1 mm半径为R1=0.9 mm宽度b1=18 mm的直圆型柔性铰链,由式(1)可得其转动刚度为E1=0.3(N·m)/rad;定义E、F柔性铰链为最小厚度t2=0.1 mm半径为R2=0.9 mm宽度b2=12 mm的直圆型柔性铰链,其转动刚度为E2=0.2 (N·m)/rad;定义支点铰链G为最小厚度t3=0.1 mm半径为R3=0.9 mm,宽度b3=18 mm的直圆型柔性铰链,其转动刚度为E3=0.3(N·m)/rad,定义刚体部分参数分别为l=60 mm、l1=10 mm及l2=60 mm。在上述参数条件下,ANSYS的位移分析结果及应力分析结果如图7和图8,其中位移单位为毫米(mm),材料应力单位为兆帕(MPa),杠杆机构自由位移端为最大位移1.04×10-5mm;在整体机构参数不变的情况下,分别通过改变铰链宽度的值改变E1、E2、E3的值及改变参数l、l1、l2的有限元分析值和理论计算值如图9~图14所示。经数据分析发现,有限元分析值与理论模型的计算值的结果相差不到5%;同样,在通过改变铰链的厚度t及半径R等参数改变柔性铰链刚度的情况下,同样可以得到有限元分析值与理论计算值的结果相差不到5%的结果,由于该理论计算模型为近似运动模型、且有限元分析方法由于有限元网络划分密度设计不同也会对计算精度产生影响,5%的差值应属合理允许误差范围,因此可以说ANSYS分析的结果验证了式(1)~式(6)的正确性。

图7 ANSYS位移分析结果图
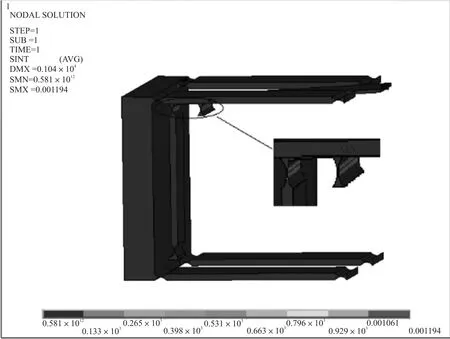
图8 ANSYS应力分析结果图
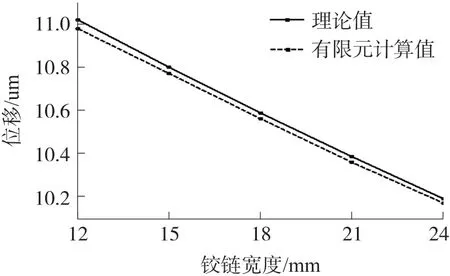
图9 改变铰链宽度b 的有限元值与理论值比较
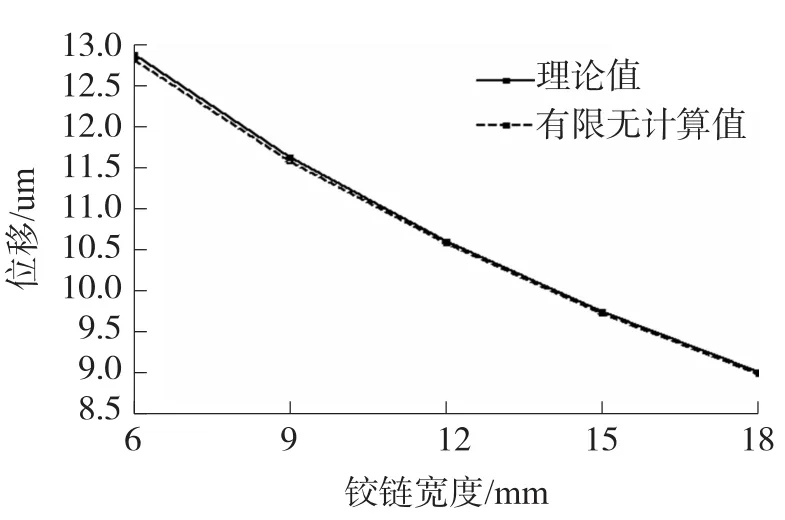
图10 改变铰链宽度b2的有限元值与理论值比较
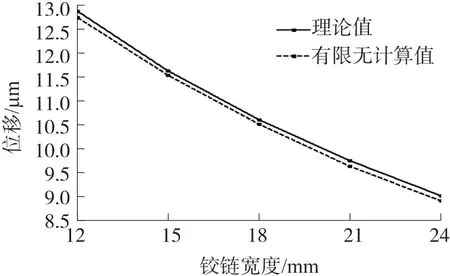
图11 改变铰链宽度b3的有限元值与理论值比较
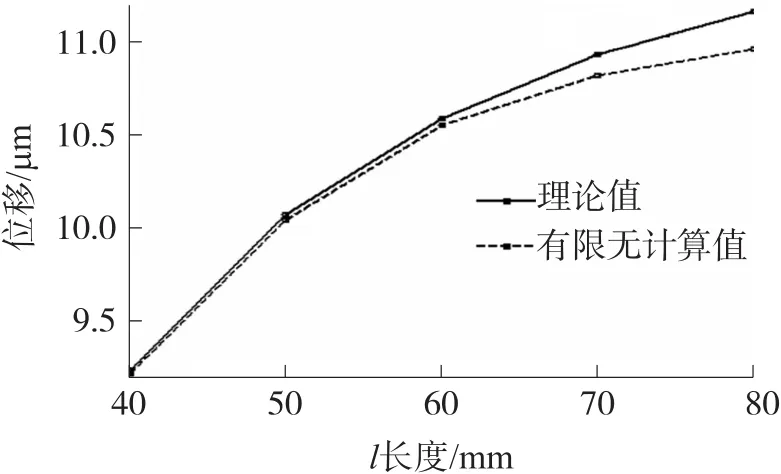
图12 改变长度l的有限元值与理论值比较
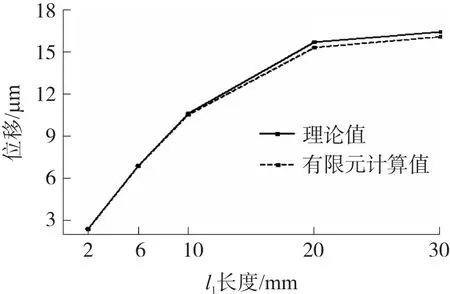
图13 改变长度l1的有限元值与理论值比较
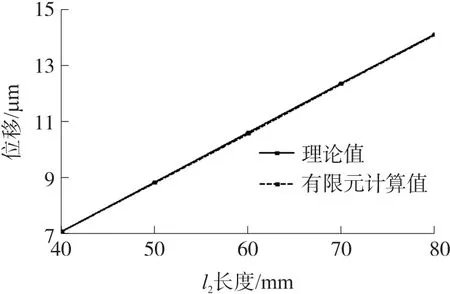
图14 改变长度l2值的有限元值与理论值比较
在实际设计中,往往由于产品需求及材料特性等因素,各项尺寸存在限制,因此,需要对各项参数进行仔细选择以提高性能指标。
式(1)~式(6)及有限元分析结果表明,在设计时,在加工能力的范围内,该平衡机构的各个铰链的刚度应尽可能小。对于结构尺寸参数的设计,如图12所示,平行四杆机构的长度l越长,杠杆右端位移越大,因此在设计时应在尺寸允许的条件下加大l的长度。对于l1和l2的设计,由于尺寸限制,l1与l2的和往往应为一个固定尺寸,因此根据式(5),可根据设计要求的放大比(即l2与l1的比值)和位移量选取l2和l1的数值。
5 设计实例
本方法在精密天平的设计中进行了实际设计应用。电子天平基本原理为杠杆平衡法称重,采用光电检测测位法和利用电磁力反馈平衡零位法原理,实现对被称物体质量的称量。
以分辨力为1 mg、最大量程为200 g的实验室天平的设计为例:首先根据电磁缸所产生的电磁力确定杠杆比及l1/l2的范围,已知天平电路的电流检测分辨力为100 nA,该电流能发生的力为10×10-7N,1 mg重物产生的重力大小为10×10-5N,因此l1/l2的值应大于1/100;已知电路能检测的最大电流为400 mA,此时能稳定产生的电磁力为4 N,最大量程200 g所产生的重力被测力为2 N,因此l1/l2的值应小于2。据便携性要求,所设计的天平机械结构的长×宽×高为50 cm×30 cm×8 cm以内;由于其内部还需放置电路板,防护罩等零件,杠杆平衡机构的空间为12 cm× 9 cm×6c m;因此,取尺寸l和a的最大值分别为长和高的2/3,即为8 cm和4 cm,l1与l2之和为9 cm。考虑到加工能力,柔性铰链的最小加工厚度存在一定限制,因此设所加工的各柔性铰链参数与有限元验证部分的个铰链参数相同。同时已知光电测位机构的分辨力为5 nm,即10×10-5N的被测力产生的位移D的值大于5 nm;根据式(6),l1的范围为大于0.29 cm小于7.34 cm,由于l1/l2的值应大于1/100且小于2,且l1、l2之和为9 cm,因此l1的取值范围应为0.29 cm 表1给出了上述约束条件下根据式(6)针对千分之一和万分之一天平分辨力时对l、l1、l2的设计结果,从结果中可以看到,在上述已知条件和选取铰链参数条件下,设计万分之一天平时,计算结果表明不存在l1及l2的参数值可使天平达到该设计分辨力,此时应该考虑适当加长l、l1+l2,或者提高位移检测机构或电路的分辨力。 表1 天平设计参数 在实际设计中,除了本文提及的柔性铰链平行四杆机构、杠杆机构和拉带机构外,还需根据加工条件及使用情况,设计装配部分、电磁缸的安装部分及校准机构等。图15为一实际设计的天平机械部分结构图。 图15 实际设计图 本文通过材料力学能量法给出了用于精密力测量中柔性铰链平衡机构的数学运动模型(6),并通过有限元方法对该数学运动模型(6)的正确性进行了验证,证明了模型的正确性,并利用该结论对电子精密天平进行了实际设计。根据所得运动模型及有限元分析的结果,分析了设计时各种参数的选择方法,为此类机构提供了设计时的理论根据。 参考文献: [1]邓志军.电子天平的原理与使用[J].理化检验:化学分册,1997,(5):225-227. Deng Z J. The Principle and Use of Electronic Balance[J],Physi⁃cal Testing and Chemical Analysis Part B(Chemical Analysis),1997,(5):225-227. [2]骆钦华,骆英.天平的发展演变[J].中国计量,2003,(9):37-40. Luo Q H,Luo Y. The Evolution of the Balance[J]. China Metrolo⁃ gy,2003,(9):37-40. [3]周兆敏,杨德邻.高精度电子天平设计中的几个问题[J].仪器仪表学报,1989,(1):3-10. Zhou Z M,Yang D L. Some Problems in the Design of High Preci⁃sion Electronic Balance[J]. Chinese Journal of Scientific Instru⁃ment,1989,(1):3-10. [4]王思民,云霞,陈军政.基于柔性铰链微位移放大机构的设计和分析[J].液压气动与密封,2011,31(1):17-20. Wang S M.Design and Analysis on Micro Displacement Magnify⁃ing Mechanism with Flexible Hinges[J]. Hydraulics Pneumatics & Seals,2011,31(1):17-20. [5]王旭,沈雪瑾,张永宇.基于柔性铰链的热驱动微夹钳的实验和仿真分析[J].传感技术学报,2006,5A(5):1559-1562. Wang Xu,Shen Xuejin,Zhang Yongyu. Experimental Analysis and Simulation of Microgripper with Flexure Hinge[J]. Chinese Journal of Sensors and Actuators,2006,05A(05):1559-1562. [6]何高法,唐一科,刘世明,等.微加速度计中新型微杠杆机构设计和分析[J].传感技术学报,2007,7:1535-1538. He Gaofa,Tang Yike,Liu Shiming,et al. A Novel Micro Leverage Mechanism Optimization for Micro Resonant Accelerometer[J]. Chinese Journal of Sensors and Actuators,2007,7:1535-1538. [7]Zou X,Guoping LI,Shen J,et al. Displacement Magnifying Mech⁃anism with Flexible Hinges Based on APDL[J]. Mechanical & Electrical Engineering Magazine,2009. [8]邵万里.精密电磁力平衡传感器设计[D].湖南大学,2012. Shao W L. The Design of Precision Electromagnetic Force Bal⁃ance Sensor[D]. Hunan University,2012. [9]梅特勒-托莱多有限公司.测力设备,特别是重量传感器:中国,99119142.0[P].1999-09-17. Mettler Toledo. Force Measuring Equipment,Especially Weight Sensor:China,99119142.0[P].1999-09-17. [10]张霖,王建华.单平行四杆柔性铰链机构刚度特性分析[J].华东交通大学学报,2013,(6):55-58. Zhang L,Wang J H. Stiffness Analysis of Single Parallel Four Bar Flexure Hinge Mechanism[J]. Journal of East China Jiaotong Uni⁃versity,2013,(6):55-58. [11]左行勇,刘晓明.三种形状柔性铰链转动刚度的计算与分析[J].仪器仪表学报,2006,27(12):1725-1728. Zuo X. Calculation and Analysis of Rotational Stiffness for Three Types of Flexure Hinges[J]. Chinese Journal of Scientific Instru⁃ment,2006,27(12):1725-1728. [12]Paros J M,Weisboro L. How to Design Flexure Hinges[J]. Ma⁃chine Design,1965,37(27):151-157. [13]吴鹰飞,周兆英.柔性铰链转动刚度计算公式的推导[J].仪器仪表学报,2004,25(1):125-128. Wu Y. Deduction of Design Equation of Flexure Hinge[J]. Chi⁃nese Journal of Scientific Instrument,2004,25(1):125-128. [14]杨敏,滕召胜,陈良柱,等.基于CS5532的高精度电子天平设计[J].仪表技术与传感器,2010,(1):14-17. Yang M,Teng Z S,Chen L Z,et al. Design of High Precision Elec⁃ tronic Balance Based on CS5532[J]. Instrument Technique & Sensor,2010(1):14-17. [15]沈剑英,杨世锡,周庆华,等.单平行四杆柔性铰链机构的输出位移和耦合误差分析[J].机床与液压,2004,(3):27-28. Shen J Y,Yang S X,Zhou Q H,et al. Analysis on the Output Dis⁃placement and Coupling Error of Single Parallel Four-bar Flexure Hinge Mechanism[J]. Machine Tool & Hydraulics,2004,(3):27-28. [16]杨启志,尹小琴,马履中,等.能量法求解全柔性微动机器人移动副的刚度[J].江苏大学学报(自然科学版),2005,26(1):12-15. Yang Q Z,Yin X G,Ma F Z,et al. Establishing Stiffness of Pris⁃matic Pair in Fully Compliant Parallel Micro-robot Using Energy Method[J]. Journal of Jiangsu University,2005,26(1):12-15. 刘庆纲(1964-),男,1987年于天津大学获得学士学位,1990年于天津大学获得硕士学位,1996年于天津大学获得博士学位,现为天津大学教授博导,主要研究方向为光电及微纳测试技术,lqg@tju.edu.cn; 孙庚(1990-),男,2013年于河北工程大学获得学士学位,现为天津大学硕士研究生,主要研究方向为微纳测试技术,sungeng@tju.edu.cn。 Kinematics Analysis and Parameter Design of Leverage Balancing Mechanism Based on Flexible Hinges* LIU Qinggang*,SUN Geng,QIN Zirui,LANG Yaopu Abstract:Leverage balance mechanism based on flexible hinges for small force measurement with mN order resolu⁃tion and N order range is described in this paper,and the motion model is derived. Finite element method(FEM,ANASYS)is used to validate the mathematical model. According to the results of both mathematical model and the FEM analysis,a conclusion that the displacement of the test force generated can be increased by reducing the stiff⁃ness of the flexible hinges and increasing the length of the parallel four-rod mechanism is obtained. Required lever⁃age ratio and motion model can be obtained by reasonably choosing the leverage length of the hinge pivot on both sides. Thus atheoretical basis for the design of the mechanism is provided. Key words:leverage balancingmechanism;Kinematics analysis;ANSYS FEM;flexible hinges doi:EEACC:7320M10.3969/j.issn.1004-1699.2016.03.002 收稿日期:2015-09-30修改日期:2015-11-21 中图分类号:TH82 文献标识码:A 文章编号:1004-1699(2016)03-0313-07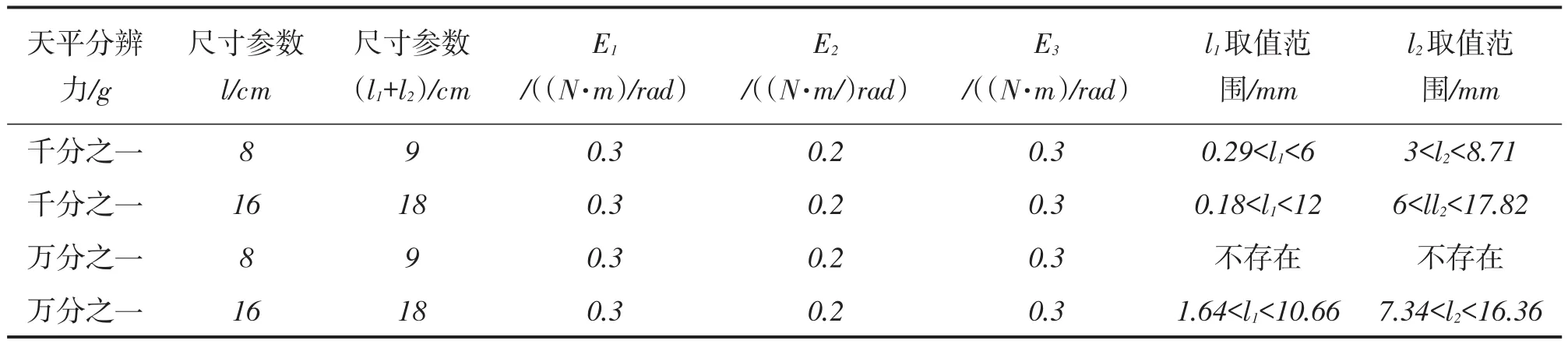

6 结论


(State Key Laboratory of Precision Measurement Technology and Instrument,Tianjin University,Tianjin 300072,China)
