一种基于目标圆的有向强栅栏构建算法*
2016-05-03车志聪范兴刚徐俊超浙江工业大学计算机科学与技术学院杭州310023
车志聪,范兴刚,徐俊超(浙江工业大学计算机科学与技术学院,杭州310023)
一种基于目标圆的有向强栅栏构建算法*
车志聪,范兴刚*,徐俊超
(浙江工业大学计算机科学与技术学院,杭州310023)
摘要:K-栅栏覆盖是有向传感器网络覆盖控制的研究热点之一。提出一种基于目标圆的分布式有向强栅栏构建方法(DBCTC)。首次构建了节点目标圆和能耗比2个模型。以节点感知区域内横坐标最大的点为圆心,以感知半径为半径的圆就是目标圆。节点的运动能耗和栅栏增益的比值就是能耗比。前一个节点根据目标圆模型选择后一个节点的最佳目标位置。从附近移动节点中选择能耗比最少的移动节点构建有向强栅栏。仿真结果证明,该栅栏构建方法比其他算法降低60%左右的能耗。
关键词:有向栅栏覆盖;目标圆;节点目标方向;下一个节点,能耗比
项目来源:“十二五”国家科技支撑计划项目(2012BAD10B01)
有向传感器,如视频传感器,超声传感器和红外传感器等,在诸多领域有着广泛的应用,如可将传感器节点部署在重要管道沿线以监视针对管道的破坏活动,以及在敌营周边布设无线传感器节点来监视敌方的兵力部署和武器配备情况等。在上述列举的应用中,有向传感器节点被部署于感兴趣区域的边界,对进入感兴趣区域的移动目标进行检测,这种技术被称为栅栏覆盖。如何实现栅栏覆盖是有向传感网络一个研究热点[1]。
利用节点的移动能力构建全向栅栏已有一些研究工作。班冬松研究了全向移动传感器网络K-栅栏覆盖问题,提出了一种能量高效的栅栏覆盖构建算法CBIGB[2]。Wang研究了节点存在定位误差时的栅栏覆盖问题[3]。He研究了多次移动节点构建栅栏覆盖[4]。范兴刚研究了全向强栅栏构建,提出了PMNSB算法[5]。在有向栅栏研究中,Ma研究了最少的有向视频节点组建栅栏问题[6];Zhang利用有向节点的转动能力构建强栅栏[7];Wang选择有向节点组建视线栅栏,构建有向传感阵列监视入侵者[8];Wang研究了混合有向网络的栅栏覆盖[9-10],根据网络拓扑构建权重栅栏图WBG,再运用顶点不相交的路径算法构造K-栅栏。以上这些方法都是集中式的,都需要知道整个网络的拓扑。Shih研究了分布式栅栏构建算法,利用可能栅栏行中的邻居节点通过栅栏信息构建栅栏[11]。Tao利用邻居节点的位置信息,选择具有最多邻居的节点构建栅栏[12]。
Amac基于移动能耗和转动能耗,研究了有向网络的覆盖增强[13]。利用附近节点之间的位置关系,分布式的选择节点构建栅栏。我们研究了NSDBC算法[14]。在此基础上,本文研究如何利用邻居节点目标圆,根据运动能耗与栅栏增加的长度比值,调度节点的运动,节能高效的构建有向强K-栅栏覆盖,提出一种基于目标圆的分布式有向强栅栏构建方法DBCTC (Distributing Directional Strong Barrier Construction Based on Target Circle)。主要贡献如下:①首次创建了节点目标圆模型,节点根据自己的目标圆和周围的移动节点,确定下一个节点的目标位置;②提出了能耗比模型,每一个节点根据能耗比选择可移动节点运动到目标位置构建有向强栅栏;
本文余下章节安排如下:第1节描述网络模型;第2节详细介绍DBCTC方法;第3节通过仿真实验对提出的算法进行性能评估;第4节总结全文并介绍下一步工作。
1 相关模型和定义
有向传感器节点方向可调感知模型可以采取四组表示
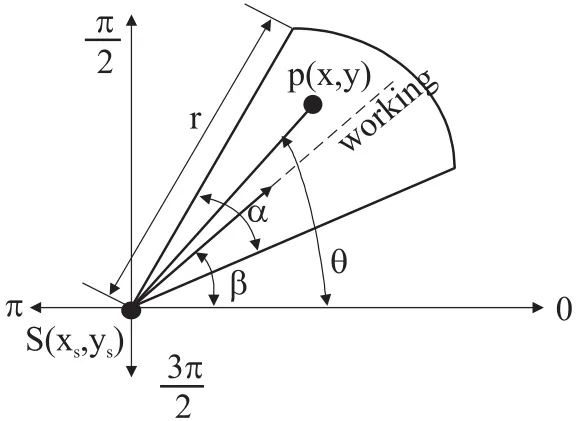
图1 可旋转有向传感器的传感模型
研究有向栅栏问题之前,有如下假设:①所有传感器的感知半径和感知角度均相同。②所有传感器的转动能耗和移动功耗均相同,参考文献[15],传感器每转动180°耗能为1.8 J,每移动1 m耗能为3.6 J。③传感器监视范围内的信号强度相同,且能在范围内以100%的可能性监测到事件。
有向节点的目标位置,有向节点运动能耗和节点密度定义分别参考文献[14]中的定义1,2,3。
定义1有向节点的目标感知方向。移动到目标位置的有向节点的感知方向就是有向节点的目标感知方向。有向节点的目标感知方向由移动到该位置的移动节点的初始感知方向决定。
定义2目标圆。以一个节点感知区域内横坐标最大的点为圆心,以r为半径的圆就是目标圆。目标圆外的移动节点只要移动到目标圆上,再转动有限的角度,就可能与前一个节点形成栅栏链接。
定义3能效比。假设移动节点的运动能耗为Ei,栅栏增加的长度为li,则能效比为λi=Ei/li,能效比越小,形成栅栏耗费的能量越小,栅栏形成算法越高效。
有向强栅栏的定义见文献[10]的定义6,我们研究的问题就是:在狭长区域中,随机部署的有向移动节点密度为γ的情况下,如何分布式地调度移动节点,以尽量少的运动能耗构建有向强栅栏覆盖。
2 基于目标圆的分布式有向强栅栏构建算法(DBCTC)
Wang[10]提出了optimal scheme算法,构建加权图,采用顶点不重复的K条路径图论算法找到形成栅栏的目标位置,然后移动节点和这些目标位置进行最佳匹配。运用节点之间的位置关系,在形成栅栏的节点集合中,按照从左到右的节点顺序,按照节点对栅栏贡献尽量最大原则,由前一个节点确定节点的目标位置,并选择能耗最少的节点移动到目标位置。从而构建有向强栅栏。这是分布式基于邻居节点运动的分布式有向栅栏构建算法(NSDBC)[14]。
另一方面,以节点感知区域内横坐标最大的点为圆心,以r为半径的圆就是目标圆,移动节点只要移动到这个目标圆上,再转动有限的角度,就可以与前一个节点形成栅栏链接。这就是DBCTC算法的基本思路。
2.1理论分析
要形成栅栏,重点和难点是确定节点目标位置。有向节点的目标位置由形成栅栏的前一个节点决定。
在第i(i≥1)个节点调度完毕后,若在其感知区域内部存在节点,横坐标最大的节点就是第i+1个节点的目标位置。例如,在图2(a)、2(b)中,节点A中,节点C的横坐标比节点D大,则节点C的坐标就是下一个节点的坐标,圆心为C的虚扇形就是第i+1个节点的目标位置。在图2(a)中,α/2≤β≤π,节点C的目标方向为β=α/2处。在图2(b)中,π<β<2π-α/2,节点C的目标方向为β=2π-α/2。
对于节点感知区域外的移动节点,则要构造目标圆来确定节点的目标位置。以感知区域内横坐标最大的点为圆心,以r为半径,构造目标圆。如果目标圆内有移动节点,下一节点的目标位置就是其坐标,这个节点再以最小的转动角度调整感知方向,使其与前一个节点形成栅栏衔接。例如,在图2(c)中,节点A中没有节点,则以节点A的感知区域内,找到横坐标最大的堤岸B,以点B为圆心构造节点A的目标圆,节点C在目标圆内,则节点C的坐标就是下一个节点的目标位置,其目标感知方向为红色的虚线扇形。
由几何知识可知,两点之间的直线距离最短,对于目标圆外的移动节点,移动节点与目标圆的圆心的连线与目标圆的交点就是下一节点目标位置。移动节点沿着与目标圆圆心的连线,用最短的移动距离与前一个节点形成栅栏衔接。
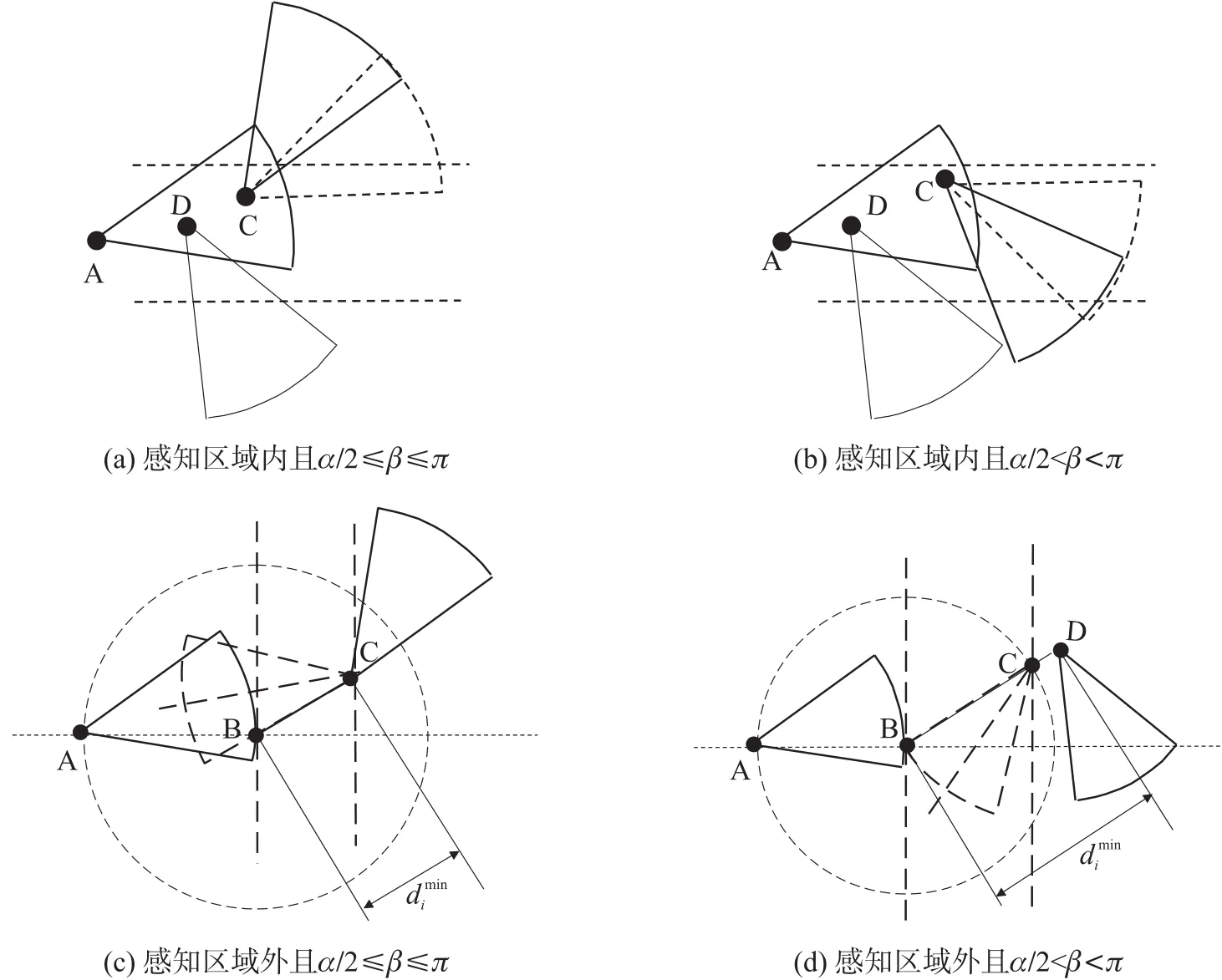
图2 节点的选择
例如,在图2(d)中,节点A的目标圆中没有节点。移动节点D在目标圆外,BD与目标圆的交点C就是下一个节点的目标位置,其感知方向为红色的虚线扇形。直线CB与X轴的夹角为θ,逆时针转动的节点C,使其与目标感知方向一直。根据文献[15]的定义2,计算节点C的运动能耗,这个时候栅栏增加的长度为l=xC-xA。
确定了节点的运动能耗和栅栏增益长度后,定义3给出了移动节点的能耗比。选出能效比最大的移动节点,移动到相应的目标位置,并以最小的转动能耗调整感知方向,形成栅栏。
2.2算法的详细过程
算法所用参数如表1所示。

表1 相关参数
DBCTC算法伪代码如图3,DBCTC算法具体步骤如下。

图3 DBCTC算法伪代码
Step 1:确定有向强栅栏的第一个节点。
选出预选区域中横坐标最小的节点。若其横坐标大于半径r,则先令其向左平行移动至横坐标等于半径,并用最少的转动能耗调整其感知方向,使其在[π-α/2,π+α/2]之间。若其横坐标小于半径,判断扇形区域与左边界x=0是否有公共点。若已有公共点,不进行转动;若无公共点,选择需要转动角度较小的那个方向,转至其扇形区域恰与左边界x=0有一个公共点。该节点调度完毕后作为该条栅栏的第1个节点。
Step 2:确定下一个节点的目标位置。Step 2.1:前一个节点感知区域内的移动节点。
根据文献[10]的定义1,判断剩余节点中,是否有节点在第1个节点扇形区域内部。若有,选出扇形区域内横坐标最大的节点作为第2个节点,不进行移动。只将其按照文献[14]的式(1)调整方向角,并计算运动能耗。例如,在图4中,节点A为第一个节点,圆心为B的虚扇形为第二个节点的目标位置,圆心为B的节点主要转动到虚线位置即成为构建栅栏的第二个节点。
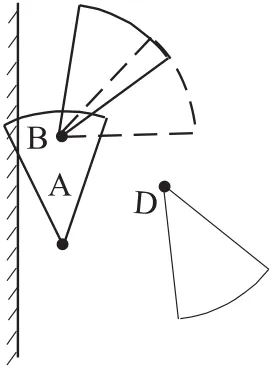
图4感知区域内节点的选择
Step 2.2:前一个节点感知区域外的移动节点。
Step 2.2.1:前一个节点目标圆内的移动节点。
若没有节点在第1个节点扇形区域内部,则将其中横坐标最大的点作为圆心,构造目标圆。如果有移动节点在目标圆内,下一节点的目标位置就是其坐标,以最小的转动角度调整感知方向,使其与前一个节点形成栅栏衔接。计算移动节点构建栅栏的能耗,和栅栏的延伸长度,计算能耗比。
Step 2.2.2:前一个节点目标圆外的移动节点。
如果目标圆内没有移动节点,对目标圆周围的移动节点进行如下的操作:先确定移动节点形成栅栏的的目标位置和目标感知方向,移动节点和圆心的连线与目标圆的交点就是下一个节点的目标位置,再根据图2确定节点的目标感知方向。计算移动节点构建栅栏的能耗,和栅栏的延伸长度,计算能耗比。
Step 3:确定移动节点的目标方向。
根据定义1确定节点的目标方向。
Step 4:确定移动节点的运动能耗。
根据文献[14]的定义2确定节点的运动能耗。
Step 5:能耗比最高的可移动节点形成栅栏。
选择能耗比最高的节点运动到目标位置,与前一个节点形成栅栏衔接。
Step 6:依次确定其余节点的目标位置,并选择能耗比最高的节点移动。
Step 7:根据右边界位置,确定形成第1条栅栏。第i+1个节点调度完后,判断≥L是否满足。若是,则该条栅栏已经形成完毕,转入Step 8;若否,则转到Step 2。
Step 8:构建其余K-1条栅栏。
若K>1,从剩余的移动节点中选择横坐标最小的节点,重复Step 2至Step 7的操作,形成第2条栅栏。同理,依次形成第3条、第4条…第K条栅栏,算法结束。
2.3算法的特点分析
如何降低栅栏形成过程中的能耗,是栅栏构建算法要重点考虑的问题。DBCTC算法通过以下措施降低能耗,高效构建栅栏:①在构建有向栅栏的节点集合中,由前一个节点根据其目标圆确定下一个节点的目标位置,不同的节点有不同的目标位置。而NSDBC算法只把前一个节点感知区域内最大的横坐标位置作为下一节点的坐标位置。②DBCTC算法根据节点的运动能耗和栅栏增益长度的比值选择移动节点运动到目标位置。而NSDBC算法只选择运动能耗最小的节点运动到目标位置。
在栅栏形成过程中,设起始为n个节点,则需要先从n个节点中选中第1个节点,然后从(n-1)个节点中选出第2个节点…以此类推,直至栅栏形成完毕。因此在整体上,时间复杂度会随着所需节点的增加而增加。最坏情况:在形成K条栅栏的过程中,若出现最坏情况,则形成K条栅栏用尽了投撒区域内全部n个节点。此时,时间复杂度O(n2)。
3 仿真结果
本文运用MATLAB 7.0对此算法进行仿真,区域大小为300 m×200 m。每组实验数据采用重复50次独立实验取平均值的方式获得。如果没有特别指明,实验的默认参数为K =2,r=10 m,a=π/4,γ=0.006,J1=3.6 J/m,J1=1.8 J/m。目前为止,最新的有向栅栏构建算法研究是文献[10]和[14],我们选取了文献[10]的strong optimal算法,文献[14]中的NSDBC算法与本文DBCTC算法进行了仿真比较。主要的性能参数是:形成的栅栏的总能耗,平均能耗,节点数。默认情况下取100次实验的平均值。
在默认参数下,给定相同的初始投撒结果,DBCTC算法如图5所示。NSDBC算法的形成的栅栏如图6所示,strongoptimal算法的形成的栅栏如图7所示。NSDBC算法仅用60~70个节点就构建了2条栅栏,而strongoptimal算法需要用110~125个节点才能构建两条栅栏。DBCTC算法用了80~90个节点形成两条栅栏。DBCTC算法的节点数要比NSDBC算法多,这是因为NSDBC算法仅仅以±α/2或者π±α/2为目标方向。而DBCTC算法目标方向是不确定的。
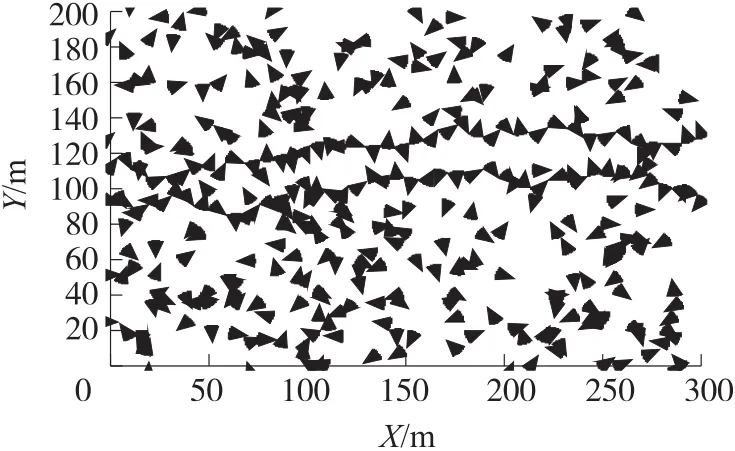
图5 DBCTC算法
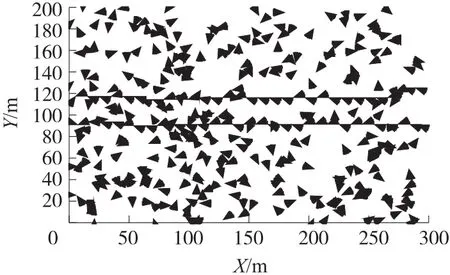
图6 NSDBC算法
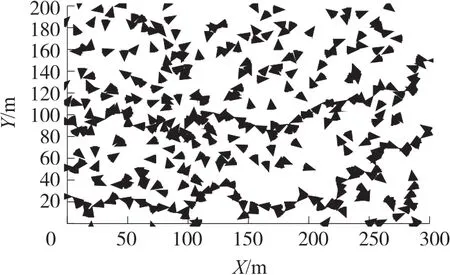
图7 strong optimal算法
3.1节点密度的影响
由于strongoptimal算法对于节点数量的要求比较高,在保证能形成栅栏的前提下,本文采用0.003作为起始节点密度进行仿真比较,其余实验参数均为默认参数。仿真结果如图8~图10所示。随着节点密度的增加,会有更多的节点位于目标圆中,从而使得DBCTC算法中不需要移动的点增加,而转动所消耗的能量要远小于移动,这导致DBCTC算法的平均能耗和总能耗会随密度的增加而减小,图8和图10表现了这一趋势。同时,由于移动节点对栅栏的期望贡献要略大于只进行转动的节点,从而只需要更少的节点构建栅栏,所以当节点密度增加时,DBCTC算法的节点个数会略微增加,图9表现了这一趋势。此外,由于DBCTC算法引入了目标圆,使得每一个节点的目标位置不在固定,因而在最优情况下DBCTC算法中每一个节点相交于NSDBC算法均少移动了一个感知距离的长度,但实际情况中,无法达到最优情况,而图10表明,相同密度下,DBCTC算法的平均能耗要比NSDBC算法低15 J~20 J,即每个节点平均少移动大约0.4~0.6个感知距离。
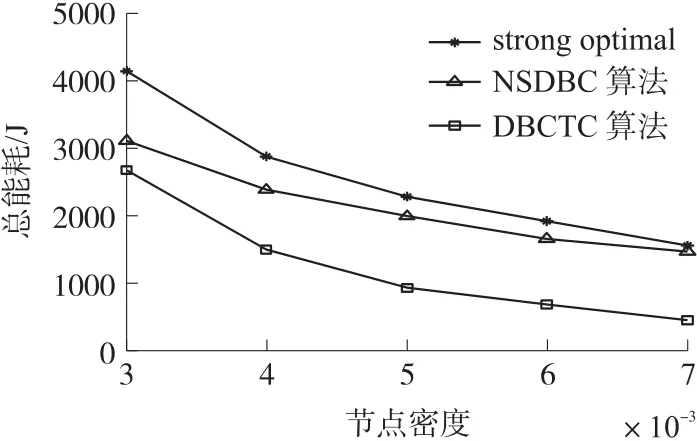
图8 节点密度VS节点总能耗
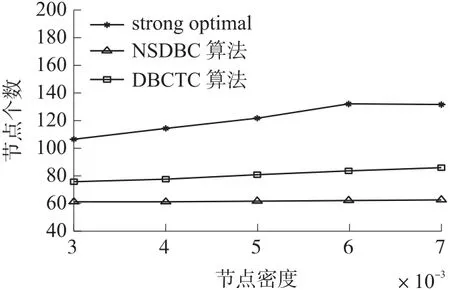
图9 节点密度VS形成栅栏所需的节点数
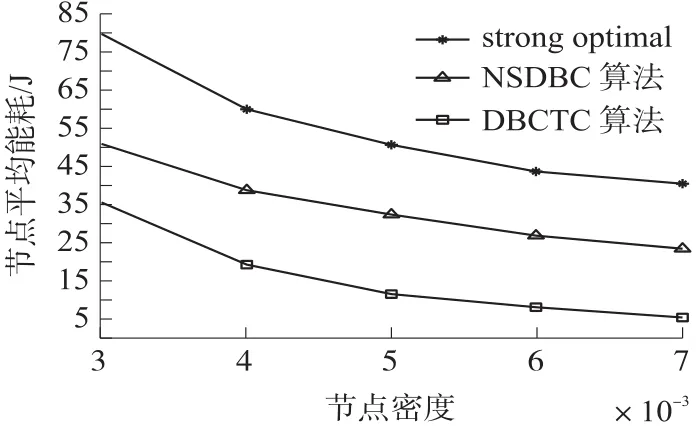
图10 节点密度VS节点平均能耗
3.2栅栏数的影响
栅栏数K的影响如图11~图13所示。从图11中可以看出,3种算法的节点总能耗均随K增大而增大,当K>3时,随着K的增大,DBCTC算法的节点总能耗将越来越低于同等条件下strong optimal算法与NSDBC算法中的节点总能耗。从图12中可以看出,随着K的增大,DBCTC算法形成栅栏所需的节点数随K的增长率明显低于同等条件下的strong optimal算法,但高于NSDBC算法。图13表明,随着K的增大,而DBCTC算法的节点平均能耗的上升幅度远低于strong optimal算法与NSDBC算法。相比strong optimal算法,NSDBC算法,DBCTC算法的平均能耗分别下降了83%,60%。
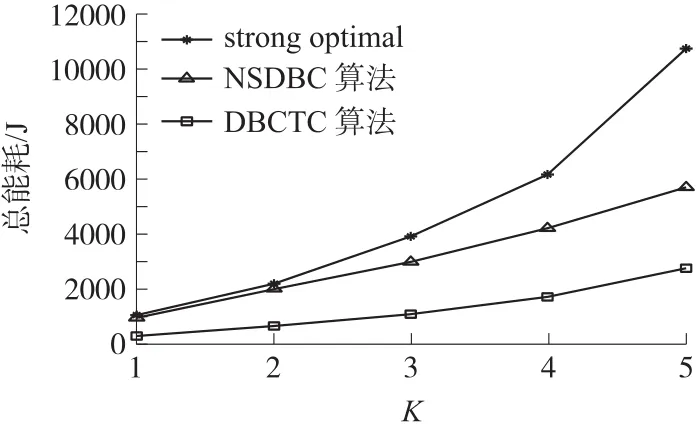
图11 栅栏数VS节点总能耗
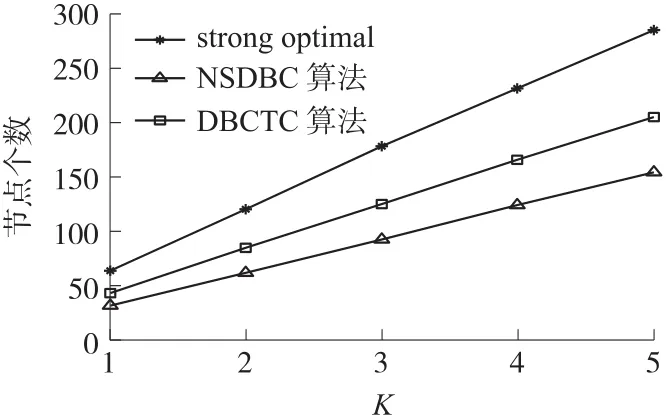
图12 栅栏数VS形成栅栏所需的节点数
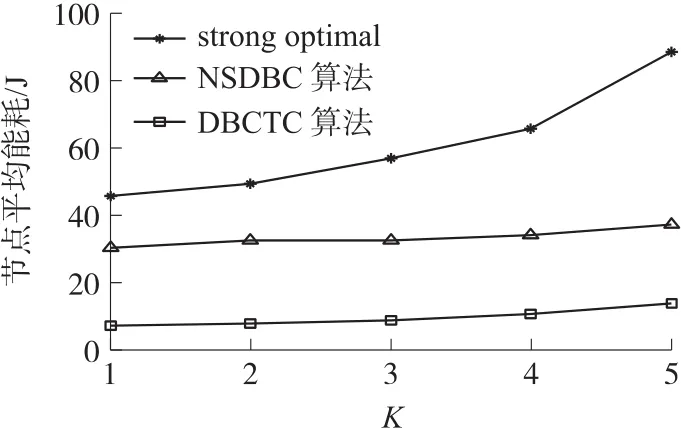
图13 栅栏数VS节点平均能耗
3.3传感器感知角度的影响
传感器感知角度改变时,对栅栏构建的影响主要在于改变了单个节点对栅栏的贡献。NSDBC算法中大部分节点对栅栏的贡献都是固定的,因而无法有效利用感知角度增加时节点感知区域增加的部分,从而导致其总能耗、平均能耗以及节点数均变化很小,如图14~图16所示。
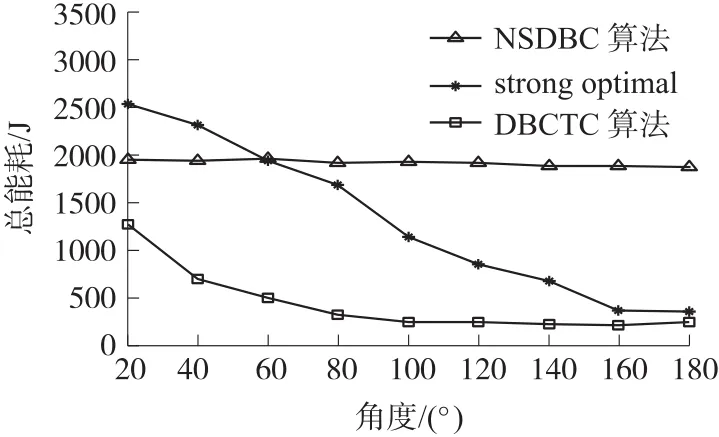
图14 感知角度VS总能耗
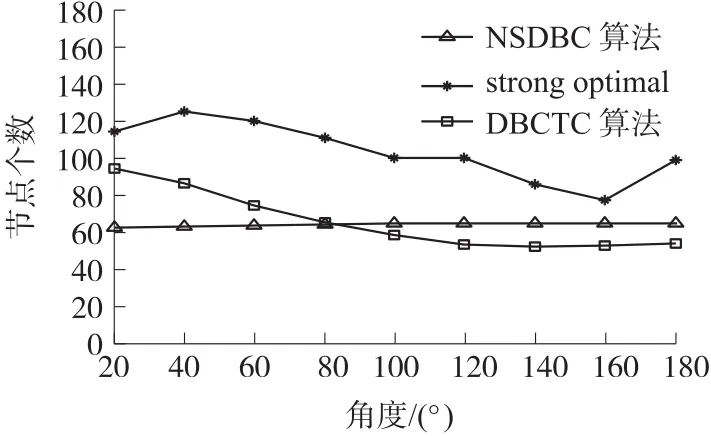
图15 感知角度VS形成栅栏所需的节点个数
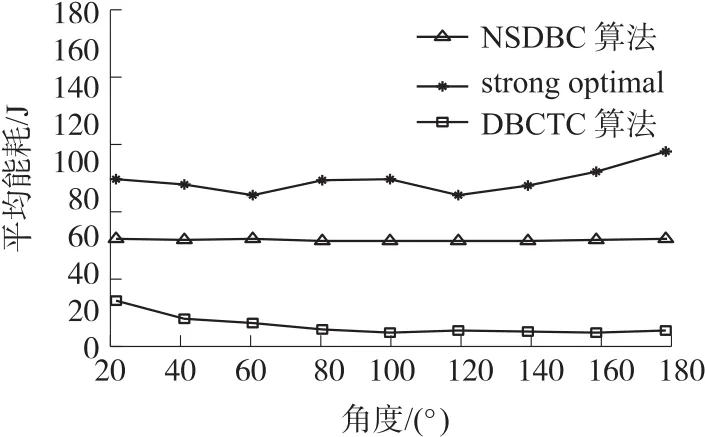
图16 感知角度VS节点平均能耗
而DBCTC则有效的利用了感知角度增加时节点感知区域增加的部分,因而,虽然在低感知角度下,DBCTC算法中单个节点对栅栏的贡献要小于NSDBC算法,但随着感知角度的增加,DBCTC算法中单个节点对栅栏的贡献会逐渐增加,直至超过NSDBC算法,这就导致了图15中低感知角度下DBCTC的节点个数比NSDBC算法高,而随着角度的增加,DBCTC的节点个数要逐渐减少直至低于NSDBC算法。同时其降低的幅度要大于strong op⁃timal算法,可知DBCTC算法对单个节点的利用要更充分。
仿真结果表明,DBCTC算法大大降低了形成栅栏节点能耗,提高了算法效率,增加了栅栏寿命。
4 结论
本文主要研究有向强栅栏覆盖问题,提出DBCTC算法,利用目标圆确定节点的目标位置。从附近节点中选择能耗比最少的节点运动到目标位置,从而分布式构建有向强栅栏。仿真结果证明DBCTC算法可以用大大降低能耗,更为高效节能地构建有向K-栅栏覆盖。
概率感知模型是更符合实际的感知模型,如何节能高效地构建概率栅栏是下一步要研究的内容。
参考文献:
[1]Tao D,Wu T Y. A Survey on Barrier Coverage Problem in Direc⁃tional Sensor Networks[J]. IEEE Sensors Journal,2015,15(2):876-885.
[2]班冬松,温俊,蒋杰,等.移动无线传感器网络K-栅栏覆盖的构建算法[J].软件学报,2011,22(9):2089-2103.
[3]Wang Z B,Chen H L,Cao Q,et al. Fault Tolerant Barrier Cover⁃age in Wireless Sensor Networks[C]. Proceedings of IEEE INFO⁃ COM,Toronto,Canada,2014:1869-1877.
[4]He S B,Chen J M,Li X,et al. Cost-effective Barrier Coverage by Mobile Sensor Networks[C]. Proceedings of IEEE INFOCOM. Or⁃lando,USA,2012:819-827.
[5]王超,范兴刚.一种高效强K—栅栏覆盖构建算法[J].传感技术学报,2015,28(2):227-233.
[6]Ma H,Yang M,Li D,et al. Minimum Camera Barrier Coverage in Wireless Camera Sensor Networks[C]. Proceeding of IEEE INFO⁃COM,Orlando,USA,2012:217-225.
[7]Zhang L,Tang J,Zhang W. Strong Barrier Coverage With Direc⁃tional Sensors[C]. Proceedings of IEEE Globe Com,Honolulu,USA,2009:1-6.
[8]Wang Y,Cao G. Barrier Coverage In Camera Sensor Networks [C]. Proceedingof ACM MobiHoc,Paris,France,2011:12.
[9]Wang Z B,Liao J L,Cao Q,et al. Barrier Coverage in Hybrid Di⁃rectional Sensor Networks[C]. Proceedings of IEEE MASS. Hang⁃hou,China,2013:222-230.
[10]Wang Z B,Liao J L,Cao Q,et al. Achieving k-barrier Coverage in Hybrid Directional Sensor Networks[J]. IEEE Transactions on Mobile Computing,2014,13(7):1443-1455.
[11]Shih K P,Chou C M,Liu I H,et al. On Barrier Coverage in Wire⁃less Camera Sensor Networks[C]. Proceeding of 24th IEEE AT⁃MA,Perth,England,2010:873-879.
[12]陶丹,陈后金.视角受限传感器网络强栅栏覆盖判定算法[J].北京交通大学学报,2010,35(5):8-11.
[13]Amac Guvensan,Gokhan Yavuz. Hybrid Movement Strategy in Self-orienting Directional Sensor Networks[J]. Ad Hoc Networks,2013,11(3):1075-1090.
[14]任勇默,范兴刚.一种有向传感器网络栅栏覆盖增强算法[J].传感技术学报,2015,28(7):10511057.

车志聪(1995-),男,本科生,主要研究领域为无线传感器网络;

范兴刚(1974-),男,副教授,工学博士,研究领域为传感器网络,网络通信、实时通信,分布式实时系统的设计,xgfan@zjut. edu.cn;

徐俊超(1995-),男,本科生,主要研究领域为无线传感器网络。
A Construction Scheme for Directional Barrier Based on Target Circle*
CHE Zhicong,FAN Xinggang*,XU Junchao
(College of Computer Science and Technology,Zhejiang University of Technology,Hangzhou 310023,China)
Abstract:K-barrier coverage is one of the hot spot in directional wireless sensor network. This paper proposes a dis⁃tributing directional barrier construction based on target circle(DBCTC). Two novel models:target circle and ener⁃gy consumption ratio are created for the first time. The center of target circle is just the point with maximum X coor⁃dinate within the sensing region of the preceding node. Its radius is always the sensing radius. The energy consump⁃tion ratio is the ratio of actuating energy consumption to barrier gain. Target location is determined by target circle. The mobile node with minimum energy consumption ratio moves to target next node location. Simulation results show this method could decrease 60% energy consumption than other method.
Key words:Directional barrier coverage;target circle;target workingdirection;next node;energy consumption ratio
doi:EEACC:6150P;6210;723010.3969/j.issn.1004-1699.2016.03.015
收稿日期:2015-09-28修改日期:2015-11-23
中图分类号:TP273
文献标识码:A
文章编号:1004-1699(2016)03-0390-07
