基于蚁群粒子群混合算法与LS-SVM瓦斯涌出量预测*

付　华，于　翔，卢万杰（辽宁工程技术大学电气与控制工程学院，辽宁葫芦岛125105）



基于蚁群粒子群混合算法与LS-SVM瓦斯涌出量预测*

付华*，于翔，卢万杰
（辽宁工程技术大学电气与控制工程学院，辽宁葫芦岛125105）

摘要：为有效预防瓦斯灾害，以预测矿井瓦斯涌出量为研究目的，提出经改进的蚁群（ACO）粒子群（PSO）混合算法优化的最小二乘支持向量机（LS-SVM），并用其预测非线性动态瓦斯涌出量。算法通过对LS-SVM的正则化参数C和高斯核参数σ进行寻优，建立了基于蚁群粒子群混合算法优化的瓦斯涌出量预测模型，并根据赵各庄矿矿井监测到的各项历史数据进行实例分析。实验结果表明：该预测模型预测的最大相对误差为1.05%，最小相对误差为0.28%，平均相对误差为0.75%。较其他预测模型拥有更强的泛化能力和更高的预测精度。

关键词：瓦斯涌出量；非线性动态预测；蚁群算法；粒子群算法；最小二乘支持向量机

项目来源：国家自然科学基金项目（51274118）；辽宁省教育厅基金项目（L2012119）；辽宁省科技攻关项目（2011229011）

瓦斯是影响煤矿安全生产的重要因素之一［1］。准确预测瓦斯的涌出量，提前采取有效的防治手段是预防煤矿瓦斯灾害的关键所在［2］。至今为止，国内外学者已经研究过多种煤矿瓦斯量涌出的预测方法。目前所使用的瓦斯量涌出预测方法有：矿山统计法、瓦斯地质数学模型法、分源预测法等线性预测方法［3］，以及卡尔曼滤波法［4］、神经网络预测法［5］、灰色系统预测法［6］、主成分回归分析法［7］、聚类分析法［8］等非线性预测方法。但不同的预测模型有着各自的优缺点，例如：神经网络模型需要选择模型和参数，存在收敛速度慢等缺点；灰色理论预测法当原始数据序列波动较大且信息过于分散时，其预测精度将会降低；聚类分析法中隶属度的确定受人为因素影响较大等问题。且上述各种方法都不能很好地解决实际问题中普遍存在的变量之间多重相关性问题。

基于上述现状，提出了基于蚁群算法ACO（Ant Colony Optimization）与粒子群算法PSO（ParticleSwarm Optimization）的混合算法优化最小二乘支持向量机LS-SVM（Least Squares Support Vector Ma⁃chine，）的瓦斯涌出量预测模型，对回采工作面瓦斯涌出量进行预测。将该预测模型应用于实际矿井中，同时与其它预测模型所预测的结果进行比对，突出了该预测模型的优点，克服了之前瓦斯涌出量预测模型的不足。

1　 LS-SVM回归算法

LS-SVM是标准支持向量机SVM（Support Vec⁃tor Machine）的一种扩展，与标准支持向量机相比，LS-SVM用等式约束取代不等式约束，求解速度快［9-10］。它采用误差ξi的二次范数作为损失函数，于是优化问题则变为：

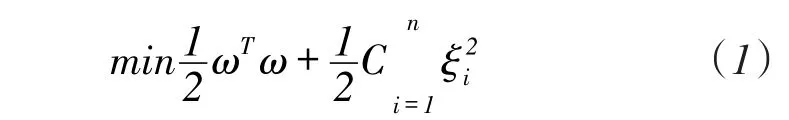
约束条件为：

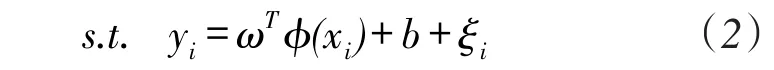
式中，ω为权向量，b为偏置量，ξi为误差量，ϕ(xi)为核空间映射函数，C为正则化参数。

引入拉格朗日乘子αi构造如下函数：

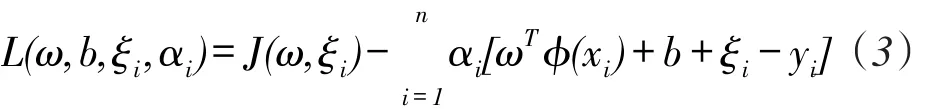
通过Karush-Kuhn-Tucker最优化条件消去中间变量得最优的αi，b值，则LS-SVM回归模型变为：

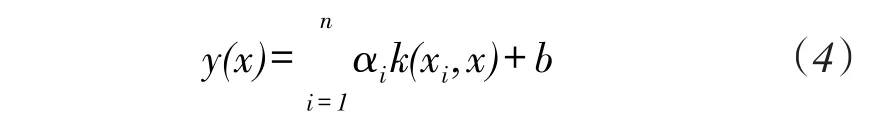
选择具有全局收敛性的高斯径向基函数作为核函数，即

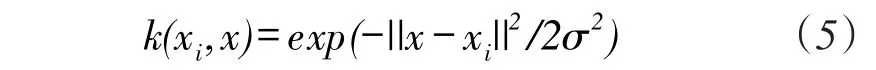
式中，σ为核宽度，在选择了核函数后，LS-SVM有待于进一步确定的参数有：正则化参数C及核宽度σ。选用蚁群粒子群混合算法对LS-SVM的正则化参数C及高斯核参数σ进行寻优。

2　蚁群粒子群算法

2.1蚁群算法

蚁群算法由意大利学者Dorigo M等人率先提出。充分利用了蚁群搜索食物过程及旅行商问题（TSP）之间的相似性，通过人工蚂蚁搜索食物的过程从而解决TSP问题［11］。

LS-SVM参数优化设计中蚁群算法的应用如下：

初始时，将m只蚂蚁放置在起点处，然后每只蚂蚁按照不同路径寻找LS-SVM的最优参数，经过n个时刻蚂蚁完成一次循环，蚂蚁遍历过程中，在每条路径上释放信息素。遍历完成后，各条路径上的信息量大小要根据下式作出调整：

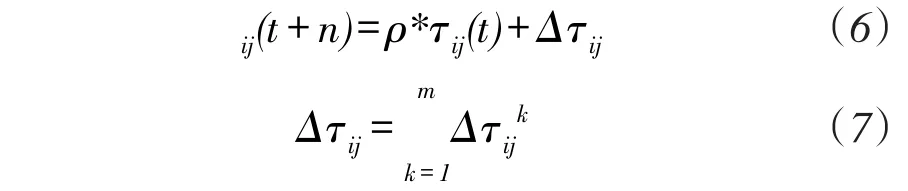
式中，Δijk表示第k只蚂蚁在本次循环中在路径ij上所留下信息量的增量，Δij表示本次循环中所有经过路径ij的蚂蚁在该路径上所留下信息量的增量，ρ为信息素挥发度。

式中，Q为常数（蚂蚁循环一次所能释放出的总信息量），Lk为第k只蚂蚁在当次循环中所经过路径的总长度。

由于该算法求解的质量取决于参数的选择，而参数的选择过于依赖于工程师的经验和主观判断，故蚁群算法关于LS-SVM最优参数的求解性能受到一定限制。

2.2粒子群算法

粒子群优化算法（PSO），由Eberhart博士及Ken⁃nedy博士提出［12-14］。算法初始化为一群随机粒子（随机解），通过迭代法找到最优解。每次迭代过程中，粒子会通过跟踪两个“极值”更新自己。一个是粒子自身所寻找到的最优解，叫个体极值即：pbest。另一个是整个种群目前所寻找到的最优解，叫全局极值即：gbest。粒子i的速度及位置更新方程如下：

式中：xi为位置信息，且xi=（xi1，xi2，..，xid）T；vi为速度信息，且及分别为粒子i在第k次迭代中的第d维的速度及位置；和 gbestkid为粒子i在第k次迭代中的第d维个体极值点的位置和全局极值点的位置；ω为调节粒子飞行速度的惯性权重因子。c1和c2分别是调节个体最佳粒子和全局最佳粒子飞行方向的学习因子。r1，2为［0，1］间的随机参数。

蚁群算法优化中粒子群算法的应用如下：将蚁群算法的重要参数值赋值给粒子群算法中的粒子位置坐标，通过粒子位置寻优后反馈到蚁群算法中，避免了蚁群算法中参数选取盲目性的问题。

3　基于蚁群粒子群混合算法与LSSVM的瓦斯涌出量预测模型

3.1基于蚁群粒子群混合算法与LS-SVM的参数优化

采用蚁群粒子群混合算法优化最小二乘支持向量机（LS-SVM），可由经验给出一组LS-SVM的参数值，对LS-SVM算法进行训练，根据目标值的大小选择可使目标值最优的参数再进行训练，直到获得满意的LS-SVM训练模型。蚁群粒子群混合算法优化LS-SVM的流程图如图1所示。

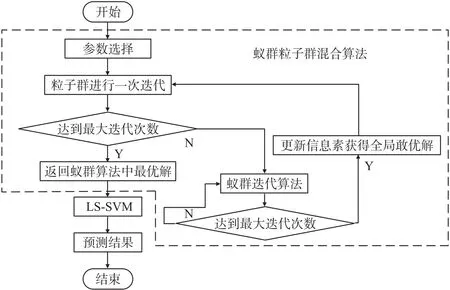
图1　算法流程图

首先，将蚁群算法中的信息素强度Q、期望值启发式因子β、信息素挥发度ρ映射到粒子群算法中，即粒子的位置坐标由三个参数来表示：

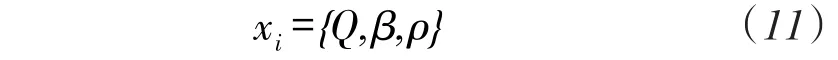
粒子的初速度随机产生，粒子每一维均对应一个速度及方向：

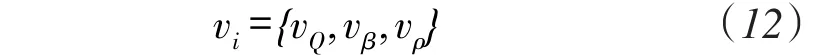
对粒子位置进行初始化后，即调用蚁群算法并完成迭代循环，通过所得到的最优解来对粒子所处位置的优劣进行判断，从而来更新粒子的速度和位置：

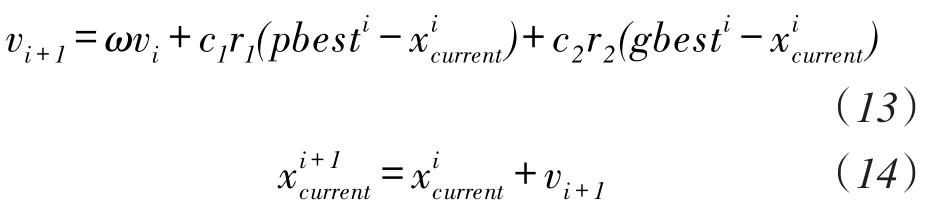
式中，vi+1为本次迭代完成后粒子的速度；及分别作为粒子在迭代前后所处的位置；pbesti与gbesti分别为当前粒子的个体极值点位置和全局极值点位置；ω为惯性权重；c1、c2分别为粒子趋向自身最优解和全局最优解的学习因子；r1、r2为随机数，取值范围为［0，1］。

其次，当粒子完成一个移步后，需要将粒子的位置坐标反馈到蚁群算法中，即再次调用蚁群算法，将粒子当前的位置坐标和各维分量分别赋值给蚁群算法中的信息素强度Q、期望值启发式因子β、信息素挥发度ρ，当粒子连续迭代若干次后仍未出现更优解，则迭代终止，返回一个全局最优解，即当前最优粒子的位置坐标，将其赋值到蚁群算法的参数中，完成优化算法。

调用蚁群算法时，当出现更优解时，才进行更新。即调用一次蚁群算法后，信息素并不清空，下一次开始调用蚁群算法时，信息素的值为上一次蚁群算法结束时的值，从而节省程序运行的时间成本。

最后，将蚁群算法所得到的最优正则化参数C和高斯核参数σ赋值给最小二乘支持向量机预测模型，得出预测结果。

3.2蚁群粒子群混合算法与LS-SVM的瓦斯涌出量预测

煤矿的瓦斯涌出量预测是一个受到多因素影响的动态非线性预测问题，选取几个重要影响因素：X1为煤层瓦斯含量，单位m3/t；X2为煤层埋藏深度，单位m；X3为煤层厚度，单位m；X4为煤层间距，单位m；X5为日工作进度，单位m/d，X6为工作面日产量，单位t/d。将上述因素作为输入样本，实时地对瓦斯涌出量Y（单位m3/min）进行预测。

利用极差化的处理方法，对训练模型的原始数据采用归一化处理，其归一区间为［0.1，0.9］，其数据归一化公式为：

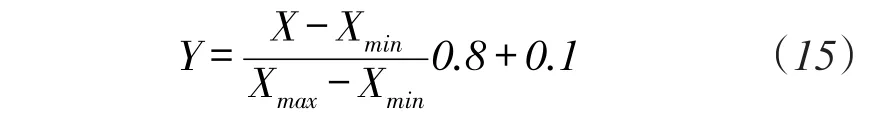
式中：X为原始数据；Xmin为原始数据的最小值；Xmax为原始数据的最大值；Y为变换后的数据。当预测运算完成后，对数据结果进行反归一化处理，其数据反归一化公式为：

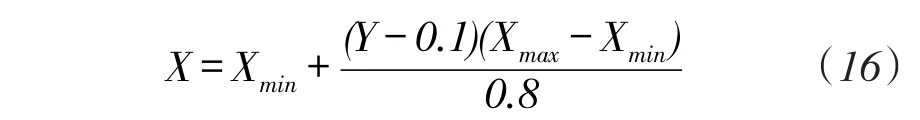
蚁群粒子群混合算法优化LS-SVM预测模型的具体预测步骤为：

第1步对训练模型输入样本的每一个重要影响因素向量按式（15）进行归一化处理。

第2步用蚁群粒子群混合算法对正则化参数C和核函数参数σ进行寻优处理，从而得到最优参数，并将其赋值给LS-SVM预测模型中训练。

第3步用训练后的LS-SVM模型对测试样本进行瓦斯涌出量预测，并将预测结果按式（16）作反归一化处理，计算预测相对误差。

4　基于蚁群粒子群混合算法与LS-SVM的瓦斯涌出量预测模型应用实例

选取赵各庄矿2013年5月至2014年12月的610组瓦斯涌出量历史监测数据进行建模分析和预测，选取对瓦斯涌出量影响作用较大的6个因素的历史数据作为预测模型的训练测试样本集。其中，前593组数据作为训练集，后17组数据用来检验预测模型的精度，具体数据见表1。

根据煤矿绝对瓦斯涌出量的影响因素，从而确定算法的初始参数如下：粒子群规模为30，学习因子c1=c2=2，惯性权重ω=0.5，蚁群数量为4个，蚁群迭代次数为30次，粒子群迭代1 000次程序终止。

表1　绝对瓦斯涌出量与影响因素数据统计

性能指标公式：

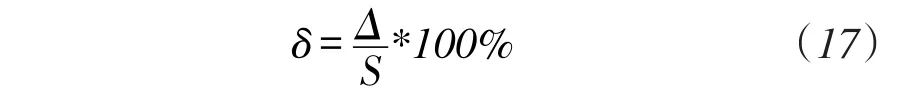
其中：δ为瓦斯涌出量预测结果相对误差，Δ为瓦斯涌出量预测结果绝对误差，S为实际瓦斯涌出量。

通过MATLAB仿真软件并结合表1数据对瓦斯涌出量预测模型进行仿真实验，得到瓦斯涌出量实际值与预测值对比图，如图2所示。

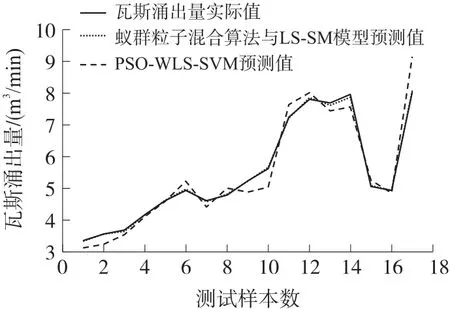
图2　瓦斯涌出量预测值与实际值对比

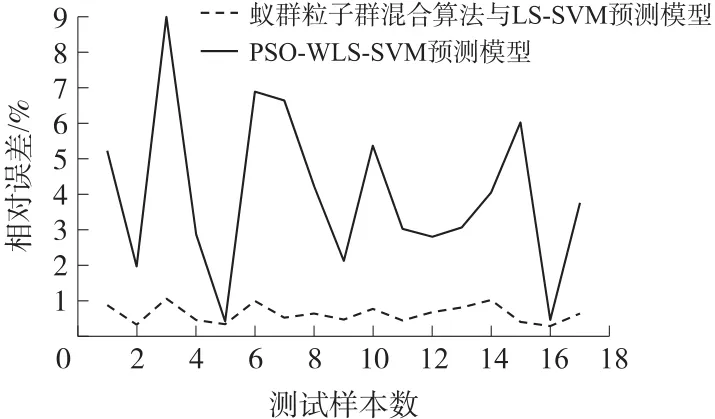
图3　预测结果相对误差

由图3可以看出，应用蚁群粒子群混合算法与LS-SVM预测模型所预测的最大相对误差为1.05%，最小相对误差为0.28%，平均相对误差为0.75%。而应用PSO-WLS-SVM预测模型预测的最大相对误差为8.99%，最小相对误差为0.41%，平均相对误差为3.97%。

由预测结果可知，蚁群粒子群混合算法与LSSVM瓦斯量涌出预测模型具有较高的预测精度和较好的泛化能力，可以准确地对矿井瓦斯涌出量进行预测，从而达到理想预测效果。

5　结论

应用蚁群粒子群混合算法，将蚁群算法的3个重要参数值赋值给粒子群算法中的粒子位置坐标，通过粒子位置寻优后反馈到蚁群算法中，解决了蚁群算法中参数选取盲目性的问题。并通过对蚁群算法进行优化，节约了时间成本。

（1）由于对煤矿瓦斯涌出量预测产生影响的因素较多，提出了蚁群粒子群混合算法与LS-SVM预测模型，对瓦斯涌出量与其影响因素之间的非线性关系进行逼近，非线性学习能力强。

（2）将蚁群算法中的信息素强度Q、期望值启发式因子β、信息素挥发度ρ映射到粒子群算法中，保证了最终得到的参数为最优参数。

（3）矿井瓦斯涌出量预测实验结果表明：基于蚁群粒子群混合算法与LS-SVM的瓦斯涌出量预测模型与同类其他预测模型相比拥有更强的泛化能力和更高的预测精度，能有效实现煤矿瓦斯涌出量动态预测的目标。

参考文献：

［1］付华，刘汀，张胜强.基于SOM-RBF算法的瓦斯涌出量动态预测模型研究［J］.传感技术学报，2015，28（8）：1255-1258.

［2］付华，訾海，孟祥云.一种EKF-WLS-SVR与混沌时间序列分析的瓦斯动态预测新方法［J］.传感技术学报，2015，28（1）：126-127.

［3］付华，谢森，徐耀松.基于MPSO-WLS-SVM的矿井瓦斯涌出量预测模型研究［J］.中国安全科学学报，2013，23（5）：56-57.

［4］王晓路，刘健，卢建军.基于虚拟状态变量的卡尔曼滤波瓦斯涌出量预测［J］.煤炭学报，2011，36（1）：80-85.

［5］朱志杰，张宏伟，韩军.基于PCA-BP神经网络的煤与瓦斯突出预测研究［J］.中国安全科学学报，2013，23（4）：45-50.

［6］董丁稳，李树刚，常心坦.瓦斯浓度区间预测的灰色聚类与高斯过程模型［J］.中国安全科学学报，2011，21（5）：40-45.

［7］吕伏，梁冰，孙维吉.基于主成分回归分析法的回采工作面瓦斯涌出量预测［J］.煤炭学报，2012，37（1）：113-116.

［8］Chang Dongxia，Zhang Xianda. Dynamic Niching Genetic Algo⁃rithm With Data Attraction for Automatic Clustering［J］. Tsinghua Science & Technology，2009，14（6）：718-724.

［9］Rubio G，Pomares H，Rojas I.A Heuristic Method for Parameter Selection in LS-SVM：Application to Time Series Prediction［J］.In⁃ternational Journal of Forecasting，2011，27（3）：725-739.

［10］乔美英，马小平，兰建义.基于加权LS-SVM时间序列短期瓦斯预测研究［J］.采矿与安全工程学报，2011，28（2）：311-315.

［11］王晓路.基于蚁群算法优化SVM的瓦斯涌出量预测［J］.煤炭技术，2011，30（5）：81-82.

［12］施式亮，李润求，罗文柯.基于EMD-PSO-SVM的煤矿瓦斯涌出量预测方法及应用［J］.中国安全科学学报，2014，24（7）：44-47.

［13］王雨虹，付华，张洋.基于KPCA和CIPSO-PNN的煤与瓦斯突出强度辨识模型［J］.传感技术学报，2015，28（2）：271-273.

［14］付华，刘雨竹，李海霞.煤矿瓦斯浓度的CAPSO-ENN短期预测模型［J］.传感技术学报，2015，28（5）：717-720.

付华（1962-），女，辽宁阜新人，教授，博士生导师，博士（后），主要研究方向为煤矿瓦斯检测、智能检测和数据融合技术。主持国家自然科学基金2项、主持及参与国家863和省部级项目30余项，发表学术论文40余篇，申请专利24项，fxfuhua@163.com；

于翔（1992-），男，辽宁抚顺人，辽宁工程技术大学电气与控制工程学院硕士研究生，主要研究方向为电气工程，2511430686@qq.com。

Prediction of Gas Emission Based on Hybrid Algorithm of Ant Colony Particle Swarm Optimization and LS-SVM*

FU Hua*，YU Xiang，LU Wanjie
（Faculty of Electrical and Control Engineering，Liaoning Technical University，Huludao Liaoning 125105，China）

Abstract：In order to prevent gas disasters effectively and predict mine gas emission，an improved LS-SVM model based on ant colony optimization mixing with particle swarm optimization was presented，which was used to predict nonlinear dynamic gas emission. The regularization C and the Gaussian kernel parameter σ of LS-SVM were opti⁃mized by the prediction model of gas emission based on hybrid algorithm of ant colony particle swarm optimization. The model was validated by using the historical data from Zhaogezhuang coal mine in China. The results show that both the maximum and minimum relative errors predicted by the model are 1.05% and 0.28% respectively，and the average is 0.75%. Compared with others，the model has higher generalization ability and predictingprecision.

Key words：gas emission；nonlinear dynamic prediction；ant colony optimization；particle swarm optimization；least square-support vector machine

doi：EEACC：723010.3969/j.issn.1004-1699.2016.03.012

收稿日期：2015-09-23修改日期：2015-11-06

中图分类号：TP391；TP212

文献标识码：A

文章编号：1004-1699（2016）03-0373-05