BeeCipher： 一种32bit分组长度的轻量级密码算法

罗宜元，　林智伟，　陈炜家，　徐禄丰

(上海电机学院 电子信息学院, 上海 201306)



BeeCipher： 一种32bit分组长度的轻量级密码算法

罗宜元，林智伟，陈炜家，徐禄丰

(上海电机学院 电子信息学院, 上海 201306)

摘要设计了一个32bit分组长度、64bit密钥长度的分组密码BeeCipher。该算法基于国际数据加密算法(IDEA)和Lai-Massey结构，对IDEA算法的32bit版本的轮函数进行了改进，添加了正交置换，使得其具有可证明安全性；修改了密钥调度过程，使得目前已有的对IDEA算法的攻击都对BeeCipher无效。BeeCipher的软件和硬件实现都很简单，其速度较目前已有的大多数 32bit 分组长度算法要快很多，是32bit分组长度轻量级分组密码中有力的候选算法。

关键词计算机安全; 密码学; 分组密码; 轻量级

BeeCipher: A 32 bit Block Length Lightweight Block Cipher

LUOYiyuan，LINZhiwei，CHENWeijia，XULufeng

(School of Electronics Information Engineering, Shanghai Dianji University，Shanghai 201306, China)

AbstractThis paper proposes a 32 bit block length, 64 bit key length block cipher BeeCipher. It is based on the structure of IDEA and Lai-Massey. The round function of IDEA-32 version is revised, and an orthomorphism added to the round function to achieve provable security. The key schedule is also updated such that all known attacks on IDEA cannot be applied to BeeCipher. Software and hardware implementation of BeeCipher is simple, and faster than most of other 32 bit block ciphers. BeeCipher can be a candidate for 32 bit block ciphers in lightweight applications.

Keywordscomputer security; cryptology; block cipher; lightweight

随着信息技术的发展，信息的安全性问题愈来愈显得突出，保证信息安全的一个重要技术就是密码学。密码学在信息安全技术中扮演着基础的角色，是攻击者最难攻破的模块。而分组密码又是密码学中最常用的算法，是信息安全中的主力，通常被称为信息安全中的驿马。目前，学术界对分组密码的设计和研究已经相当成熟，每年都有很多新的加密算法推出。由于物联网等相关技术的进步，人们发现传统的加密算法已经在资源受限的环境中无法得到广泛应用，因此，对资源消耗较少、实现效率较高的轻量级密码算法的设计已经成了学术界关注的热点。

对于轻量级密码算法的设计，目前常用的算法的长度都是64bit长度的，如PRESENT[1]、LED[2]、PRINTCipher[3]、Twine[5]，LBlock等[6-7]。而在某些特殊应用下，用户会需要32bit分组长度的分组密码，如：

(1) 一个网站系统的数据库用户ID在数据表中是用32bit整型数字来表示的，网站系统希望在用户访问的统一资源定位符(Uniform Resource Locator, URL)中标明这些ID，但同时不想让其他用户知道这些ID的数量。因此就使用一个32bit分组长度的加密算法对这些ID进行加密，然后将加密后的URL发给用户，使得用户无法查看ID的数量。同时，当用户使用相应的URL访问网站时，系统会进行相应的解密，并调出相应的用户ID。

(2) 需要将一组按序排列的32bit整数加密成另外一组无序排列的32bit的整数，同时具备一定的安全性。

对于64bit的密钥长度，穷举攻击需要264次加密过程，对于非政府或非军事组织而言，还是很难破译的。因此，目前64bit密钥的算法对于抵抗个人和小型组织的攻击还是具有一定的安全性。

目前，已有的轻量级算法主要采用Feistel结构及其扩展和代换置换网络(Substitution Permutation Network, SPN)结构，如PRESENT采用SPN结构，LBlock主要采用的是Feistel扩展结构等。除Feistel和SPN结构外，还有一类比较成熟的分组密码设计结构，即Lai-Massey结构[8]，以国际数据加密算法(International Data Encryption Algorithm, IDEA)、FOX算法为代表[9-10]。其中，IDEA在经过20多年的密码分析后，提出了Biclique攻击方法[11]。该方法将攻击复杂度降低到穷举攻击复杂度的1/4，且对于Biclique攻击，AES算法也不能幸免。因此，IDEA算法还是一个很安全的算法。其安全性建立在3个不相合的代数群运算上。其主要运算是对16bit的数据块进行异或、模216加法、模216+1乘法运算。由于这3个运算各自在不同的代数群上，结合律、分配律均不适用，从而使得IDEA算法的混淆速度非常快，在经过4.5轮迭代后，就能抵抗差分分析攻击。IDEA算法的缺陷是其密钥调度过于简化，只有简单的线性移位，故目前所有针对IDEA的攻击都是利用其密钥调度的缺陷。

原始的IDEA算法的上层结构并不具有理论意义上的伪随机性，故文献[8]中对IDEA算法的结构进行了微小的改动，添加了一个正交置换，从而使其具有理论意义上的伪随机性，而且将该结构称为Lai-Massey结构。Lai-Massey结构被证明经过3轮后具有伪随机性，4轮后具有强伪随机性。

本文基于IDEA和Lai-Massey结构设计了一种32bit分组长度、64bit密钥长度的分组密码BeeCipher。该算法不仅对IDEA算法的32bit版本，且对其轮函数进行了修改，添加了正交置换，并修改了密钥调度过程，从而使得目前已有的针对IDEA算法的攻击均对BeeCipher无效。BeeCipher的软件实现也非常简单，其速度较目前已有的大多数32bit分组长度算法要快很多。

1BeeCipher算法的描述

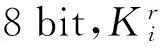
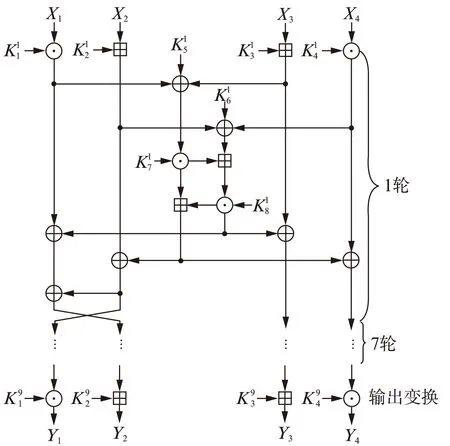
图1　BeeCipher加密过程Fig.1　Encryption of BeeCipher

图中，有3种运算方式：

(2) 字节加法运算，即模28下加法运算，用符号表示；

1.1BeeCipher加密过程

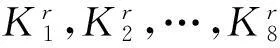
1.2BeeCipher解密过程

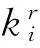
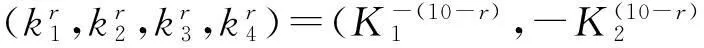
1.3BeeCipher的密钥调度过程

密钥调度将64bit的主密钥分为8个ByteK1，K2，…，K8。BeeCipher加密时一共需要68个Byte的子密钥，则第一轮子密钥为

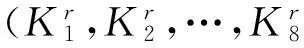
(1) 令第r+1轮子密钥中

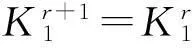
其中，Primes是小于整数256的54个素数集合，即Primes[54]={2，3，5，7，…，251}，由i=0开始，以后每运行一次乘法操作后将i递增，即i=i+1；

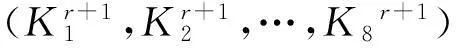
(3) 重复步骤(1)和(2)直到i=8，然后将r+1轮子密钥循环左移13bit。

(4) 一直到生成了68个子密钥为止。

2BeeCipher算法的设计原则与安全性

2.1Lai-Massey结构与IDEA结构

BeeCipher算法是基于Lai-Massey结构设计的。Lai-Massey结构与IDEA结构不同，图2给出了Lai-Massey结构与IDEA结构的对比。

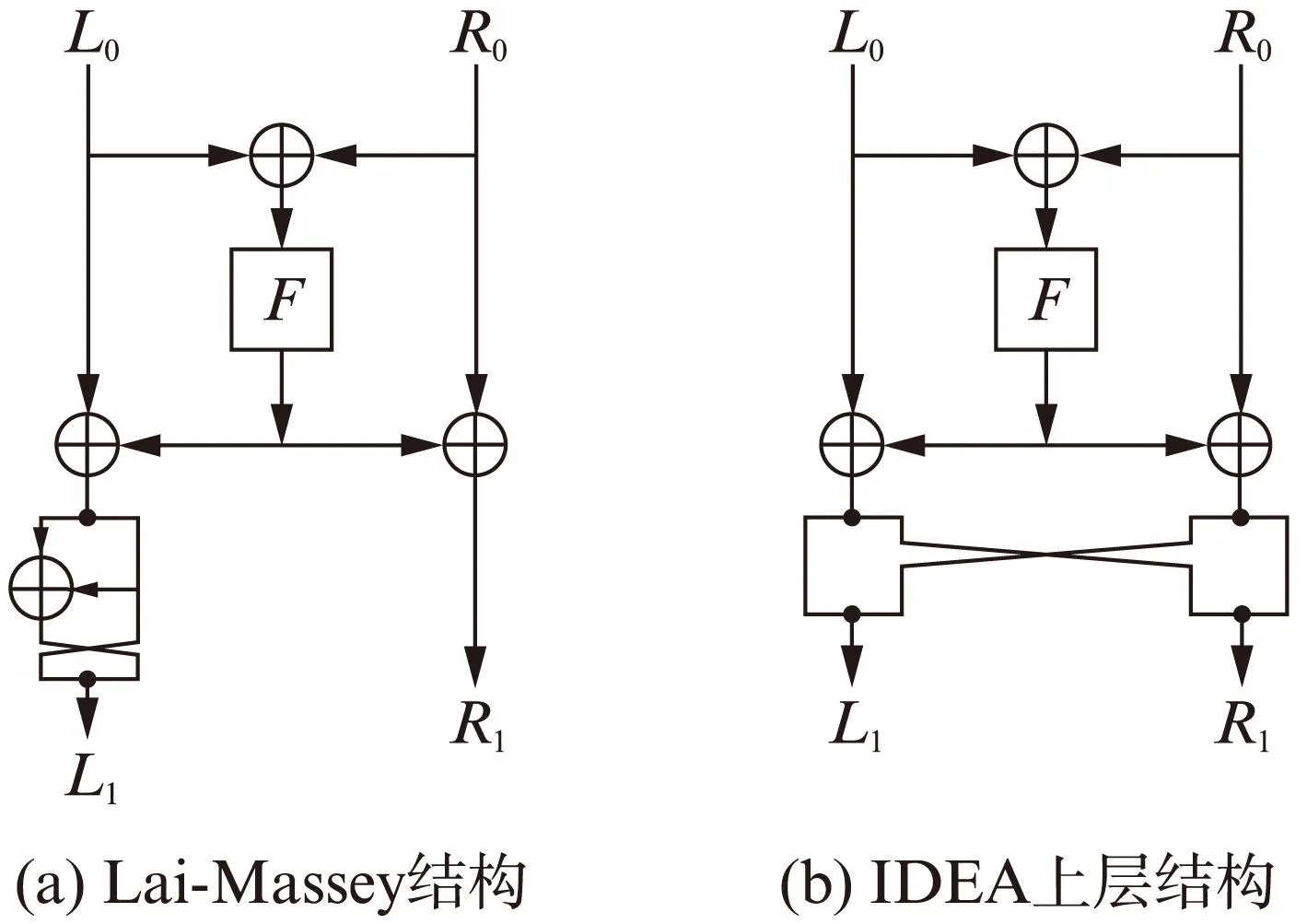
图2　Lai-Massey结构与IDEA上层结构对比图Fig.2　Lai-Massey scheme and IDEA high-level

由图可见，在Lai-Massey结构中，每轮左边的值都增加了一个正交置换；而IDEA的上层结构只是将左边数据块的右半部分与右边数据块的左边部分进行了对称交换。

对于Lai-Massey结构，Vaudenay等[6]已经证明了以下定理。

定理1在轮函数F为独立随机函数时，3轮Lai-Massey结构构成一个伪随机置换，4轮Lai-Massey结构构成一个强伪随机置换。

对于如图2(b)所示的IDEA上层结构，由于采用了以下的攻击方法，故无论迭代多少轮都无法达到伪随机性。

攻击对于一轮IDEA上层结构，若输入为

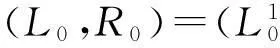
输出为

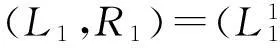
若F的输出为(f1‖f2)，则有

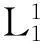
故可见无论经过多少轮迭代，攻击者都可以使用上面的攻击方法将其与一个伪随机置换区分开来。

值得注意的是，由于IDEA算法使用了不相容群上的运算，具有很强的混淆性，因此此处的攻击并不表示IDEA具体算法不能达到伪随机性，而是指其上层结构无法达到伪随机性。若IDEA算法轮函数的输入与密钥的运算都在一个群上进行攻击，如将IDEA轮函数中最上面的明文与密钥的运算改为异或运算，则IDEA算法将无法达到伪随机性。

BeeCipher对IDEA算法做了相应修改，在 IDEA 算法的基础上增加了正交置换，并在理论上证明BeeCipher的结构具有强伪随机性，且其同时具有IDEA算法的在不同群上运算的强混淆性，因此BeeCipher的安全性要强于32bit版本的IDEA算法。

2.2安全性分析

2.2.1弱密钥分析目前对IDEA的所有攻击都利用了IDEA密钥调度过于简单的弱点。在BeeCipher的密钥调度中，使用了类似非线性移位寄存器的方法，每一个新生成的字节密钥都由之前的密钥经过不同群上的模乘和异或运算得出。由于在28+1上的模乘与GF(28)上的异或运算不兼容，使得两者混合起来具有很高的非线性，故BeeCipher不存在类似于IDEA的弱密钥。

2.2.2差分分析与线性分析BeeCipher是IDEA的32bit版本的改进版。文献[10]中使用了马尔科夫链理论证明了8bit和16bit版本的 IDEA 算法在经过4轮后就能抵抗差分分析，并猜想32bit与64bit也是如此。就目前已有的对 IDEA 的攻击结果来看，IDEA对差分分析的抵抗能力的确很好。

对于线性分析，由于BeeCipher采用了群上的不兼容运算，其非线性度非常高；文献[10]中证实了MA结构，也就是图1中轮函数中最中间的结构是具有完美的混淆性，因此，BeeCipher对线性分析具有很强的抵抗能力。

2.2.3Biclique攻击Biclique攻击是目前最成功的攻击，能够成功地应用在IDEA和AES上，这是由于利用的IDEA和AES算法的密钥调度的混淆速度都不是很快，而BeeCipher的密钥调度混淆速度却相当快，使得Biclique攻击无法奏效。

综上分析可知，BeeCipher较32bit的IDEA算法更安全，且能达到最优的安全性，即对BeeCipher的最好攻击是穷举攻击。64bit的安全性能够满足对手是非政府组织和非军事组织，安全性需求不太高，但又具有一定安全性，特别的，其可以应用在超市、购物商场上。

3BeeCipher算法的实现效率

由于BeeCipher所有的运算都是字节运算，故无论是软件实现，还是硬件实现，都很简单。本文将其实现效率与其他算法进行了比较。为了实现算法的公平对比，故在同一个运算平台上实现，所用平台为HP个人PC，CPU为Intel i5-5200U 2.20GHz。表2给出了运行加密算法100万次所耗时间对比，同时给出了各算法的特征。其中，除AES128算法外，其他均为32bit分组长度的算法；Skip32算法由Greg Rose[12]基于Skipjack设计，KATAN算法由Canniere等[13]设计，SIMON和SPECK算法等由美国国家安全局[14]设计。

由表可见，KATAN32与KATANTA32算法的软件实现速度很慢，这主要是因为它们是硬件平台实现的算法；BeeCipher算法的软件实现速度较Skip32算法快了3倍多，较AES128算法快了25倍多；虽然较美国国家安全局(NSA)最新设计的SPECK32和SIMON32算法慢了约40%，但SIMON32和SPECK32算法正受到大量攻击，且公众对NSA不够信任，其安全性受到很大威胁。由于BeeCipher算法所有的运算都是字节运算，且硬件实现也很方便，故认为BeeCipher在32bit长度分组密码中是很有竞争力的候选算法。

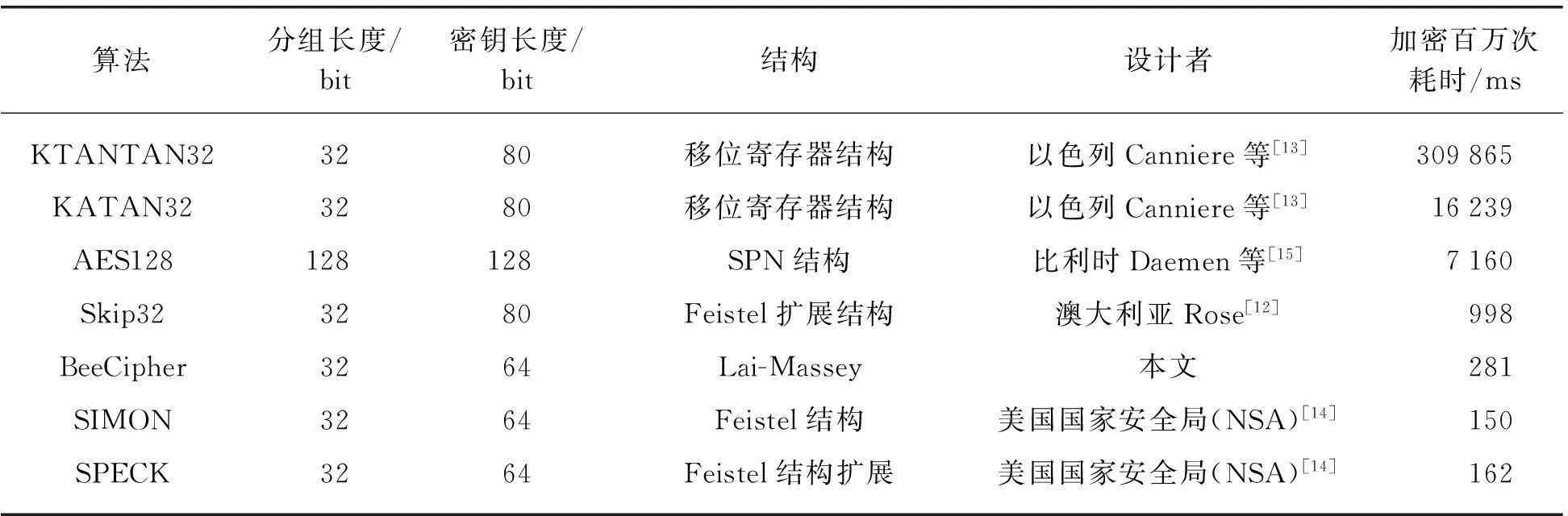
表1　不同算法的特征及运行耗时对比

4结语

本文主要设计了一个32bit分组长度，64bit密钥长度的分组密码算法BeeCipher，并且对BeeCipher的安全性做出了分析。BeeCipher是对32bit IDEA算法版本的改进，在轮函数中增加了正交置换，从而使得结构具有可证明安全性；同时，采用了IDEA算法中良好的乘法、加法混淆模块，增加了算法混淆性，并且修改了密钥生成算法，避免了线性密钥调度过程，从而使得最新的Biclique攻击对BeeCipher不成立。在软件实现上，BeeCipher算法比其他大多数32bit分组算法要快很多，只比美国国家安全局最新设计的SIMON和SPECK慢了40%左右。在硬件实现上，BeeCipher也非常容易。考虑到美国国家安全局设计的算法目前还未被验证具有良好的安全性，因此，BeeCipher是一个有力32bit分组长度的候选分组密码算法。

参考文献

[1]BOGDANOV A，KNUDSEN L R，LEANDER G，et al.PRESENT：An ultra-lightweight block cipher[C]∥Proceedings of the 9th International Workshop on Cryptographic Hardware and Embedded Systems.Berlin，Heidelberg：Springer-Verlag，2007： 450-466.

[2]GUO Jian，PEYRIN T，POSCHMANN A，et al.The LED Block Cipher[C]∥Cryptographic Hardware and Embedded Systems-CHES 2011：Proceedings of the 13th International Workshop.Berlin，Heidelberg：Springer-Verlag，2011： 326-341.

[3]KNUDSEN LR，LEANDER G，POSCHMANN A，et al.PRINTcipher：A block cipher for IC-Printing[C]∥Proceedings of the 12th International Conference on Cryptographic Hardware and Embedded Systems.Berlin，Heidelberg： Springer-Verlag，2010： 16-32.

[4]LEANDER G，PAAR C，POSCHMACNN A，et al.New lightweight DES variants[C]∥Fast Software Encryption：Proceedings of the 14th International Workshop.Berlin Heidelberg: Springer，2007： 196-210.

[5]SUZAKI T，MINEMATSU K，MORIOKA S，et al.TWINE： A lightweight block cipher for multiple platforms[C]∥Proceedings of SAC 2012.Berlin，Heidelberg： Springer-Verlag，2012： 339-354.

[6]WU Wenling，ZHANG Lei.LBlock： A Lightweight block cipher[C]∥Proceedings of the 9th International Conference.Berlin，Heidelberg：Springer，2011： 327-344.

[7]郭建胜，罗伟，张磊，等.LBlock码的不可能差分密码性能分析[J].电子与信息学报，2013，35(6)： 1516-1519.

[8]VAUDENAY S.On the Lai-Massey scheme[C]∥International Conference on the Theory and Application of Cryptology and Information Security.Berlin，Heidelberg：Springer，1999： 8-19.

[9]JUNOD P，VAUDENAY S.FOX：A new family of block ciphers[C]∥11th International Workshop，Heidelberg：Springer Berlin，2004： 114-129.

[10]LAI Xuejia，MASSEY J L，MURPHY S.Markov ciphers and differential cryptanalysis[C]∥Advances in Cryptology-EUROCRYPT’91：Proceedings of the Workshop on the Theory and Application of Cryptographic Techniques.Berlin，Heidelberg：Springer，1991： 17-38.

[11]BOGDANOV A，KHOVRATOVICH D，RECHBERGER C.Biclique cryptanalysis of the full AES[C]∥Proceedings of the 17th International Conference on the Theory and Application of Cryptology and Information Security.Berlin，Heidelberg：Springer，2011： 344-371.

[12]ROSE G.Skip32：A 32-bit block cipher based on Skipjack[EB/OL].[2015-08-12].http：∥www.qualcomm.com.au/PublicationsDocs/skip32.c.

[13]CANNIERE C，DUNKELMAN O，KNEZEVIC M.KATAN and KTANTAN-A family of small and efficient hardware-oriented block ciphers[C]∥Proceedings of the 11th International Workshop on Cryptographic Hardware and Embedded Systems.Berlin，Heidelberg：Springer-Verlag，2009，272-288.

[14]BEAULIEU R，SHORS D，SMITH J，et al.The SIMON and SPECK families of lightweight block ciphers[EB/OL].(2013-06-19)[2014-05-18].http：∥eprint.iacr.org/2013/404.pdf.

[15]DAEMEN J，RIJMEN V.The Design of Rijndael：AES-The advanced encryption standard[M].Berlin，Heidelberg：Springer-Verlag，2002： 25.

文献标识码A

中图分类号TP 309.7

文章编号2095 - 0020(2016)01 -0038 - 05

作者简介：罗宜元(1986-)，男，讲师，博士，主要研究方向为密码学，E-mail： luoyy@sdju.edu.cn

基金项目：国家自然科学基金项目资助(61402280)；上海电机学院重点学科资助(13XKJ01)；上海市大学生创新活动计划项目资助(A157011501201062)

收稿日期：2015 - 07 - 27