表贴式多相永磁电动机的优化设计分析

2016-04-29王敬莆徐余法孙明伦

上海电机学院学报 2016年1期

关键词：优化设计

王敬莆，　徐余法，　孙明伦，　张　宙

(1. 上海电机学院电气学院, 上海 201306；

2. 上海电气集团上海电机厂有限公司, 上海 200240)

表贴式多相永磁电动机的优化设计分析

王敬莆1，徐余法1，孙明伦2，张宙2

(1. 上海电机学院电气学院, 上海 201306；

2. 上海电气集团上海电机厂有限公司, 上海 200240)

摘要传统方法设计表贴式多相永磁电动机需要花费大量的时间和精力。建立了表贴式多相永磁电动机的最优化设计数学模型，选取8个优化变量，并确定了合适的取值范围。针对一台多相永磁电动机，利用遗传算法给出了2种优化设计方案，并分析验证了优化算法的灵活性和有效性。

关键词多相永磁电动机; 优化; 设计

Analysis and Optimization of Surface Mount Multi-Phase Permanent Magnet Motor

WANGJingpu1，XUYufa1，SUNMinglun2，ZHANGZhou2

(1. School of Electrical Engineering, Shanghai Dianji University, Shanghai 201306, China;2. Shanghai Electric Group Shanghai Electric Machinery Co., Ltd., Shanghai 200240, China)

AbstractTraditionally designed surface-mount multi-phase permanent magnet motor takes much time and effort. Optimization design of a surface-mounted multi-phase permanent magnet motor is established. Eight optimal variables are selected, and a suitable range determined. Two optimal designs are given using genetic algorithm. Flexibility and efficiency of the optimization algorithm are verified.

Keywordsmulti-phase permanent magnet motor; optimization; design

多相永磁电动机作为永磁电动机与多相电动机的结合，兼具两者的优点；具有高功率和转矩密度、高效率、高可靠性和易于实现低压大功率的特点，非常适合应用于大容量低速直接驱动场合[1]，如风力发电、船舶电力推进等，因此，其在低速直接驱动领域有着广泛的应用前景。

目前，对于多相永磁电动机的设计多采用传统的设计方法，要调整得到其最优的设计方案，往往需要花费大量的时间和精力[2]。对于采用最优化原理进行电动机的优化设计，国外已经有了广泛而深入的研究[3-4]，不同之处在于优化算法的选择上。传统的优化算法都是由初始点附近的有关优化信息引导，然后逐步逼近最优解，如模式搜索法[5]、共扼梯度法[6]、单纯形法[7]、可变容差法[8]和复合形法[9]等。本质上这些算法的所得结果都是局部最优解，它们在处理多峰函数时，很容易收敛于局部极值点，只能靠丰富的经验来选取较优的初始点，因此，主观性较强，不利于推广。目前，应用于电动机优化设计的多为全局优化方法，如模拟退火法[10]、遗传算法[11]等。其中，遗传算法是一种模拟生物进化过程的全局收敛算法，它通过与生物遗传、进化相似的步骤，通过选择、复制、重组、交叉、变异等，模拟自然界生物“优胜劣汰，适者生存”的现象，达到优化目的，具有通用性好、全局性、鲁棒性好等特点[12]。本文采用遗传算法进行电动机的优化设计。

本文建立了表贴式多相永磁电动机[13]的最优化设计数学模型，选取了8个优化变量，并确定了变量合适的取值范围，通过调用电动机设计和性能分析程序完成了最优化设计，通过改变目标函数可以灵活地实现电动机的不同优化目标。

1电动机优化数学模型

电动机最优化设计是带有多个不等式约束的非线性规划问题，其数学规划模型一般有3个要素：目标函数、设计变量和约束条件。

1.1目标函数

目标函数主要有两个特点： ① 无法直接用解析式表达；② 常是多峰函数，具有多个极值点。采用最优化设计方法的一个很大的优点就是目标函数的选取非常灵活，可根据要求方便地设定，仅需要修改目标函数和相应的约束条件即可，不会触及电动机的分析程序。本文选取电动机所用材料的加权质量为目标函数，即

f(x)=k1Mm(x)+k2Mfe(x)+k3Mcu(x)

(1)

式中，x=(x1，x2，…，xs)T，其中，i=1,2，…，s为电动机的设计变量；Mm(x)、MFe(x)和MCu(x) 分别为永磁体、硅钢片、铜的质量(kg)；k1、k2和k3分别为相应的加权因子，通过改变3个因子的数值可以灵活地实现各种材料最优组合[6]。

1.2设计变量及权值范围

在确定设计变量时，应考虑该变量是否独立存在、对目标函数或约束函数的影响是否足够大[14]。此外，在不显著影响优化效果的前提下，变量数目应尽可能地少，以节省计算时间。本文中，电动机的优化设计选取了8个变量，如表1所示。

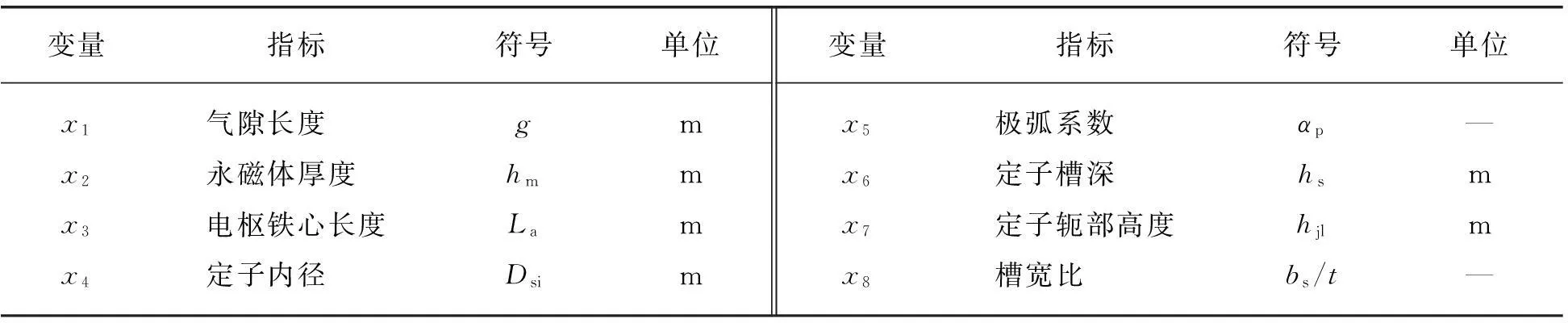
表1　电动机的优化设计变量

优化设计变量需要解决以下问题： ① 变量数量级差别过大，需要做归一化处理；② 需要确定各变量的区间中心，即参考值；③ 各变量的变化幅度。为此，本文采用尺度变换系数法[15]进行设计变量的取值。

尺度变换矩阵为

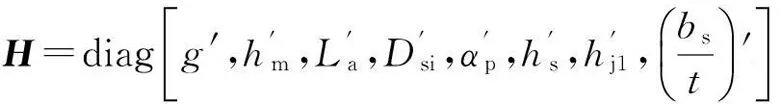
(2)

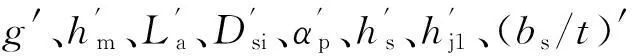
采用尺度变换矩阵可以实现设计变量的标幺化，得标幺值X=xH-1。设计变量标幺化后的数值接近1，为保证优化效果，可以选择变量范围为[0.5,2]，但是，αp和bs/t的实际值不能大于1。

1.3约束条件

永磁电动机的约束条件主要是指电动机的技术要求和保证电动机性能的其他一些限制，它反映了国家和用户对电动机技术性能的要求。不同容量的电动机具有不同的有效线负荷。本文以大型永磁推进电动机为例，为保证较高的功率密度，线负荷A取80kA以上。电动机热负荷A·J的选取同其冷却条件密切相关，其中，J为电流密度。由于多相永磁电功机的功率较大，属于大型电动机，故参考水轮发电机的相关数据，本文取A·J=300A2/mm3[16]。另外，多相永磁电动机的部分参数如下：相数m=12，额定功率P=4.5MW，额定转速n=180r/min。

本文将电动机的效率η、功率因数cosφ、额定转矩TN、最大转矩倍数kT、最小气隙长度gmin、热负荷A·J、齿部磁通密度Bt以及轭部磁通密度Bj1作为其性能约束。本文研究的永磁推进电动机性能参数如下：η0=0.97，cosφ0=0.84，TN0=238.73kN·m，kT=2.5，A·J0=300A2/mm3，Bt0=1.5T，Bj10=1.5T。则约束条件g1(x)～g8(x) 如下：

(3)

1.4惩罚函数

为对多相表贴式永磁电动机进行设计优化，本文采用罚函数法将有约束最优化问题转化为无约束最优化问题[17-18]。由于优化算法是求目标函数的最大值，故无约束最优化下的目标函数为

(4)

式中，ai为不同约束条件的加权系数，且ai>0。

2多相表贴式永磁电动机的优化与分析

本文对一台多相表贴式永磁电动机采用遗传工具箱求解其数学模型，并利用Matlab软件进行最优化仿真求解，并给出了2个优化方案。

方案1。以永磁电动机的质量f1为优化目标，在功率一定的情况下，实现电动机功率密度的最大化，选取k1=k2=k3=1。

方案2。以永磁电动机的有效材料成本f2为优化目标，设永磁体、铜和硅钢片的价格比为10∶2∶1，选取k1=10,k2=2,k3=1。

表2给出了多相表贴式永磁电动机优化前、后的设计变量比较。表3给出了Id=0时多相永磁电动机优化前后的性能比较。

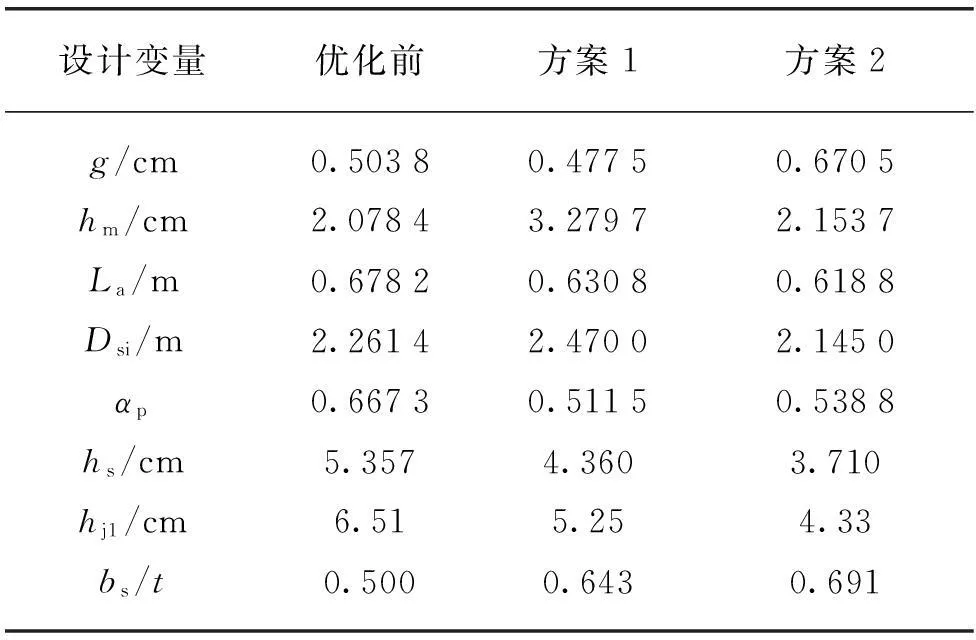
表2　优化前、后的设计变量比较

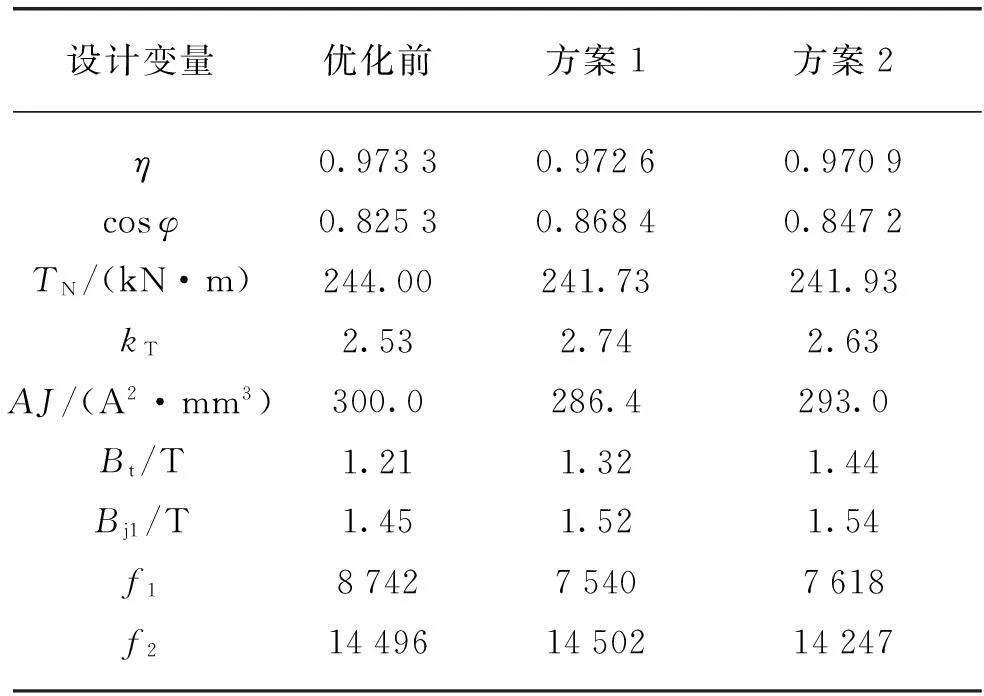
表3　优化前、后的电动机性能比较

由表2、3可见，方案1的电动机质量最小，方案2的电动机有效成本最小，且电动机的cosφ和kT都较优化前有所提高，同时基本满足了电动机的性能约束，证明了遗传算法优化电动机的灵活性和有效性。

通过优化前后各方案的比较，可以得到以下的结论：

(1) 减小hs可在降低电动机质量的同时降低电动机的效率。这是由于减小hs可以减小定子外径，从而减小整个电动机的质量；但是，为了确保A·J不超标，必须通过增加槽宽来维持槽面积的基本恒定，从而导致齿部过窄，使磁通密度增加，相应地铁耗也增加，最终导致电动机效率降低。因此，由表2可见，优化前、方案1和2的电动机效率随hs的减小依次减小。

(2) 增大hm与有效气隙长度ge之和(hm+ge)有利于增加永磁电动机的cosφ和kT，但同时会增加永磁体的用量。这是由于当采用Id=0控制时，

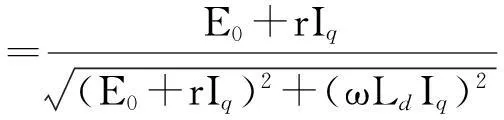
(5)

式中，E0为电动势；r为相电阻；Iq为交轴电流；Ld为电枢电感；ω为转速。理论推导也表明，hm+ge与Ld成反比，故增大hm+ge有利于增加永磁电动机的cosφ，而与最大转矩Tmax成正比。由表1、2可知，优化前、方案2和方案1的cosφ和kT随hm+ge增加依次增加。

图1给出了2种优化方案的遗传进化曲线。由图可见，遗传算法经过10代进化后进化结果开始稳定，平均结果同最好结果基本重合。

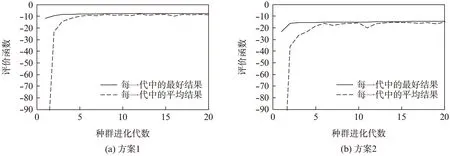
图1　2种优化方案的遗传进化过程Fig.1　Two genetic evolution processes of optimization

4结语

本文建立了多相表贴式永磁电动机的最优化数学模型，选取了优化设计变量并确定了取值范围；利用罚函数法将有约束最优化问题转化为无约束最优化问题。采用遗传工具箱求解数学模型，给出了两种不同的优化方案，其优化结果证明了优化算法的灵活性和有效性。表明使用最优化原理设计多相表贴式永磁电动机，不仅准确、高效，且可根据不同设计要求灵活地设置目标函数，有效地降低了对设计人员经验的依赖，同时可在更大设计变量范围内、更大程度地接近电动机的最优解。

参考文献

[1]张岳,王凤翔.直驱式永磁同步风力发电机性能研究[J].电机与控制学报,2009,13(1)： 78-82.

[2]程福秀.现代电机设计[M].北京：机械工业出版社,1993： 10-32.

[3]Bianchi N,Bolognani S.Design optimization of electric motors by genetic algorithms[J].IEE Proceedings of Electric power Applications.1998,145(5)： 475-483.

[4]Bouchikhi E H E,Choqueuse V,Benbouzid M E H.Current frequency spectral subtraction and its contribution to induction machines’ bearings condition monitoring[J].IEEE Transaction on Energy Coversion,2013,28(1)： 135-144.

[5]倪有源，黄亚，郎旭初，等.采用拟牛顿法和模式搜索法优化爪极发电机[J].微特电机，2013,41(3)： 15-18,23.

[6]朱丽娜，王广军，陈红.采用共轭梯度法求解多变量稳态传热反问题[J].中国电机工程学报，2011,31(8)：58-61.

[7]丛爽，冯先勇.基于GA和单纯形法的直流电机参数辨识[J].控制工程，2009,16(1)： 109-112.

[8]吴新振，金明.可变容差法在单相电机优化设计中的应用[J].微特电机，1996(4)： 24-25,34.

[9]邹琳，夏巨谌，胡国安.基于复合形法的混合多目标遗传算法研究[J].计算机应用研究，2006(7)： 70-72.

[10]孟大伟，周美兰.模拟退火算法在电机设计中的应用[J].电机与控制学报，2001,5(3)： 154-158,162.

[11]俞国燕,郑时雄,刘桂雄,等.复杂工程问题全局优化算法研究[J].华南理工大学学报(自然科学版),2000,28(8)： 104-110.

[12]肖曦,许青松,王雅婷,等.基于遗传算法的内埋式永磁同步电机参数辨识方法[J].电工技术学报,2014,29(3)： 21-26.

[13]王秀和.永磁电机[M].北京：中国电力出版社,2007： 124-136.

[14]唐任远.现磁代永电机理论与设计[M].北京：机械工业出版社,1997： 54-60.

[15]周美兰, 孟大伟. 容量自适应电动机优化设计[J]. 中国电机工程学报,2003，23(5)： 132-135.

[16]白延年.水轮发电机设计与计算[M].北京：机械设计出版社,1982： 102-116.