海口湾可见光遥感测深方法研究
2016-04-27张晓冬张文静朱首贤曾文华
张晓冬,张文静,朱首贤,曾文华
(1.河海大学 港口海岸与近海工程学院,江苏 南京210098;2.解放军92292部队,山东 青岛 266000;3.解放军理工大学气象海洋学院,江苏 南京 211101)
海口湾可见光遥感测深方法研究
张晓冬1,2,张文静3,朱首贤1,曾文华3
(1.河海大学港口海岸与近海工程学院,江苏南京210098;2.解放军92292部队,山东青岛266000;3.解放军理工大学气象海洋学院,江苏南京211101)
摘要:以海口湾为研究区,利用Landsat资料进行可见光遥感测深方法研究。采用NDW I、MNDW I、EW I、NW I指数的阈值分割法进行水陆分离,结果表明NDW I指数更适合海口湾。选取与水深相关性比较好的反射率因子TM2、TM3、TM1/TM2、TM1/TM3,采用目前常见的可见光遥感测深方法,建立了线性、对数、幂指数、指数测深模型,与实测水深的比较结果表明TM1/TM3的指数测深模型在0-10 m水深的平均绝对误差为1.67 m,在实际应用中有参考价值。此外,建立了TM2、TM3、TM1/TM2、TM1/TM3的二次多项式测深模型以及对数二次多项式测深模型,建立了它们的二元和四元线性、对数测深模型,还建立了它们的分段函数测深模型,与实测水深的比较结果表明,二次多项式测深模型优于线性测深模型,对数二次多项式测深模型优于对数测深模型,分段函数测深模型优于非分段函数测深模型。
关键词:海口湾;可见光;水深遥感
近岸海域船舶运输、港湾建设、水产养殖、围海造田、铺设电缆管道、军事活动和科学研究等都依赖于水深资料。常规水深测量方法是使用船舶进行逐点测量,费用高,难度大,更新速度慢。遥感测深方法具有覆盖范围大、快速观测的特点,为动态获取大面积海域的水深信息提供了可能,对于船舶不能进入的浅滩和争议海域也能实现水深测量。
近岸海域常见的遥感测深方法主要有机载激光测深、航空双介质摄影测深、SAR图像测深和可见光遥感测深(申家双等,2002)。机载激光测深和航空双介质摄影测深精度高,但是它们以飞机作为观测平台,对人力和物力要求高。SAR图像测深可以采用卫星资料,对人力和物力要求不太高,但是需要一定数量的常规水深和流场观测资料作为支撑,要求成像时的潮流流速应大于0.5 m/s,风速在3~12m/s。可见光向水中传播的光辐射强度随着水体及水中悬浮粒子的吸收和反射作用逐渐减弱,利用卫星传感器接收的辐射强度与水深、水体浑浊度之间的关系可以判断水深。可见光遥感资料源丰富,测深方法比较简单,在很多海域得到应用(张东等,2008;曹瑞雪等,2004)。可见光遥感测深模型的种类很多,根据构建水体测深遥感模型原理的不同,主要分为理论解译模型、半理论半经验模型、统计相关模型和人工神经网络模型等方法(王艳娇等,2007)。其中,统计相关模型计算过程简单而且不需要水体内部的光学参数,应用最为广泛。根据统计相关模型所采用的波段数可以分为单波段法(Benny et al,1997)、双波段比值法(John et al,1983)和三波段法(Hengle et al,1991),所采用的数学公式一般分为线性、对数、幂指数、指数。
本文以海口湾为研究区,根据可见光遥感光谱特征分析,参考目前常见的可见光遥感测深方法,建立了单波段和双波段比值的线性、对数、幂指数、指数测深模型。此外,拓展建立了单波段与双波段比值的二次多项式测深模型、单波段与双波段比值混合的多元因子测深模型、单波段与双波段比值的分段函数模型,并且对这些测深模型进行综合比较。
1可见光遥感测深的基本原理
太阳光辐射能量经过大气层时,被大气吸收、反射和散射后减弱,传输到水体表面时,少部分被水面反射回大气中,大部分入射到水体内部。入射到水体内部的光,大部分被水体吸收,部分被水体中的悬浮物(如泥沙、有机质等)反射,因此不断衰减,只有少部分光能透射到水底,被水体底质吸收和反射,被悬浮物反射和水体底质反射的辐射光,部分穿过水体折回到大气中。因此卫星传感器所接收到的光辐射能量就由大气后向散射光、大气反射光、水面反射光、悬浮物反射光和水底反射光等部分组成。其中,反映大气信息的大气后向散射光和大气反射光可以通过大气校正来消除;水面反射光只与水体表面状况有光,悬浮物反射光则反映了水体中悬浮物的信息,此两者可以利用深水区的光辐射能量来近似代替;水底反射光是水下地形的直接反映,是遥感探测水深的主要信息源。
在假设水质和底质都是均质的情况下,卫星传感器接收到的一个窄幅波段的光辐射能量与水深之间的关系,可以表示为:
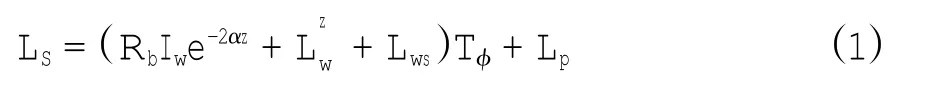
其中,Rb为底质的反射率,Iw为进入水体的光能,α为光在水体中的衰减系数,z为水深,Lzw为水体内部反射的光能,Lws为被水面反射的光能,Tφ为大气透射率,Lp为大气后向散射能量。设L∞为传感器接收到的第i波段的深水区光谱值,它为水-气界面反射的辐射能量、水体后向散射的辐射能量以及大气后向散射的辐射能量之和,即:

由式(1)和式(2)得:

(3)式表明了传感器接收到的经大气和水体削弱的光辐射能量与水体深度之间的关系,这是可见光遥感测深技术的理论基础。
对于某一个窄幅光谱波段,利用(3)式求得水深的表达式:

式中,(LS-L∞)/Iw近似等于经大气校正后得到的第i波段的反射率。式(4)进一步写为:

(5)式即为单波段测深模型。选取常规水深资料和对应的单波段反射率资料为样本,采用最小二乘法确定系数a和b,然后利用(5)式探测整个研究区的水深。
研究表明,虽然水体衰减系数和水底反射率随着水体类型和底质类型不同有很多差别,但是通过两个波段比值在一定程度上可以消除这种差异。假设存在两个波段,对应不同底质类型,这两个波段的各种底质反射率比值不变。同时假设这两个波段的水体衰减系数的差值对不同类型的水体基本保持恒定。根据(3)式,可以给出:

对(6)式两边取对数,得到水深的计算公式:

(7)式为双波段比值测深模型,它可以在一定程度上消除水质不均匀引起的衰减系数不同和底质差异引起的水底反射率不同的影响。
对双波段比值方法进行扩展,如果假设n个波段的底质反射率满足:

同时假设这n个波段的水体衰减系数对不同类型的水体满足:

则可得到多波段测深模型:

(5)和(7)式给出的单波段和双波段比值测深模型,都是采用对数公式。实际海水的水质特征复杂,光谱强度变化并不是严格按照(3)式变化,其它类型公式,例如线性公式、指数公式、幂指数公式,在测深模型中也得到应用。本文还采用二次多项式建立单波段和双波段比值测深模型。(10)式给出的多波段测深模型利用某些波段的反射率计算水深,本文还综合采用单波段和双波段比值因子建立多元测深模型。
本文采用Landsat卫星遥感影像建立测深模型。Landsat的TM1、TM2、TM3、TM4波段处于可见光波长范围,对水体穿透性比较好。TM5、TM6、TM7波段处于中红外和热红外波长范围,基本上被水体完全吸收。因此,在利用Landsat影像建立可见光遥感测深模型时,一般选择TM1~TM4波段或其组合为参数。
2研究区域和资料选取
本文研究区域如图1所示,范围为110°12'-110°18'E、20°1'-20°5'N,面积约为60 km2。水深资料从2003年实测的1∶60 000水下地形图(海图)中获得,共608个实测水深数据,水深变化范围为0~25m。选取的遥感影像资料为2004年12月20日的Landsat5 TM遥感影像(如图2),与实测水深数据的观测时间相差不大,根据遥感影像对应的潮位对海图水深数据进行潮汐订正。对该遥感影像进行辐射定标、FLAASH大气校正和几何校正等预处理后,得到各波段的反射率。
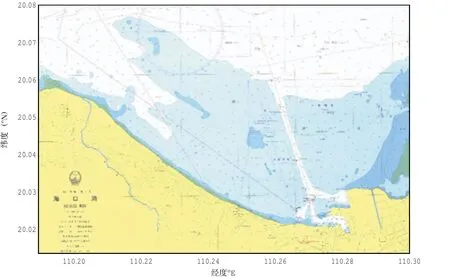
图1 海口湾实测水下地形图

图2 海口湾2004年12月20日的Landsat5 TM遥感影像
3水体信息的提取
在进行可见光遥感测深之前,需要利用可见光遥感影像进行水陆分离,提取水体信息。在可见光遥感影像上,可以根据水体和陆地的光谱差异进行水陆分割。目前常用的方法有边缘检测法、阈值分割法和监督分类法三大类(朱长明等,2013),水体指数阈值分割法简单快捷而被广泛使用。常见的水体指数有NDW I(归一化水体指数)(McFeeters,1996)、MNDW I(改进型归一化水体指数)(徐涵秋,2005)、EW I(增强型归一化水体指数)(闫霈等,2007)和NW I(新型归一化水体指数)(丁凤,2009),表达式分别为:
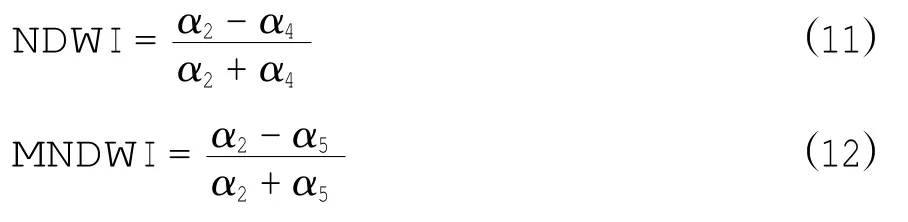

α1、α2、α4、α5、α7分别对应Landsat 5的TM1、TM2、TM4、TM5、TM7波段的反射率。本文还采用Landsat8 OLI遥感资料提取水体信息,α1、α2、α4、α5、α7分别对应Blue、Green、NIR、SW IR1、SW IR2波段的反射率。
利用水体指数阈值分割方法提取水体信息的步骤为:首先,利用水体指数公式对遥感影像进行波段运算,得到灰度值影像;其次,选择阈值0,对灰度值影像进行二值分割,灰度值大于0时为水体,并将灰度值重置为255,灰度值小于0时为陆地,并将灰度值重置为0,得到水陆分离的二值化影像;然后,采用拉普拉斯滤波算法对二值化影像进行边缘增强处理;最后,对边缘增强后的影像进行二值分割,并将栅格数据转化为矢量数据,得到水陆分界线,进而提取水体信息。
为了检验和选取适合海口湾的水体指数公式,于2013年11月20日作了水边线观测。观测方法为观测人员手持GPS,沿水边线行走,记录各个时刻水边线位置。观测时间为10∶00-10∶30,该时间段潮位为233~239 cm,取其均值为236cm。查找海口湾历史遥感影像,2013年10月26日上午11∶00的Landsat8OLI影像成像时潮位231 cm,与观测水边线的潮位非常接近。采用(11)-(14)式分别计算该Landsat 8 OLI影像的水体指数NDW I、MNDW I、EW I和NW I,并利用水体指数阈值分割法提取水边线。遥感水边线上各点与观测水边线的最近距离可以当作遥感水边线的误差,表1给出了各种水体指数公式提取的遥感水边线误差统计,综合比较最大误差和平均误差,可以看出NDW E指数提取的遥感水边线误差比较小。所以本文采用NDW I阈值分割法提取海口湾的水体信息。

表1 各种水体指数公式提取的水边线误差统计(单位:m)
4可见光遥感测深模型的建立及检验
将所有的608个实测水深数据按水深值从小到大排序,并依次分到A、B两组,A组水深数据用于相关性分析和建立模型,B组水深数据用于检验。对A组水深数据和对应站位的反射率因子(单波段反射率或双波段反射率比值)做相关性分析。相关系数计算公式为:
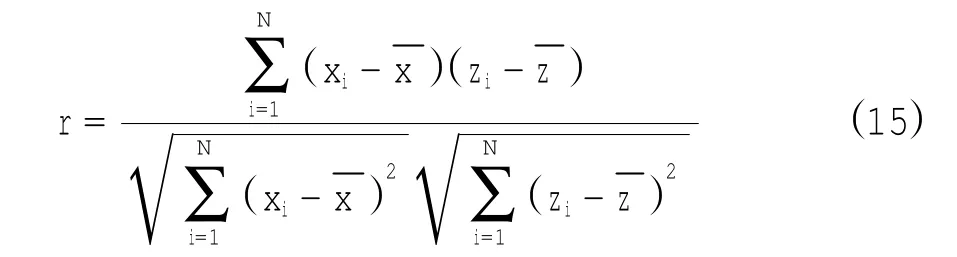
r为相关值,xi为反射率因子,为反射率因子的均值,zi为实测水深值;为实测水深的平均值;N为水深点总个数。表2给出了各反射率因子与水深的相关系数,在单波段中,TM2、TM3和水深相关性比较好,相关系数分别为-0.61和-0.60;在双波段比值中,TM1/TM2、TM1/TM3和水深相关性比较好,相关系数分别为0.71和0.70。
选取TM2、TM3、TM1/TM2、TM1/TM3的遥感数据,利用A组水深数据,分别建立线性、对数、幂指数、指数形式的测深模型,然后采用B组水深数据对各模型进行检验。表3给出了各测深模型的参数和误差统计,图3给出了单波段和双波段比值的线性、对数、幂指数、指数测深模型的检验情况。总体来看,在水深小于10m时测深效果更好,在水深大于10m时测深效果差一些。各种遥感数据进行比较,TM1/TM2和TM1/TM3与水深的相关性高于TM2和TM3与水深的相关性,TM1/TM2和TM1/TM3的测深效果也优于TM2和TM3。各种拟合公式进行比较,幂指数和指数测深模型的优于线性和对数测深模型,尤其是水深小于10m时,前两种类型测深模型的效果更佳。在水深小于10m时,TM1/TM3的指数测深模型误差最小,其平均绝对误差为1.67m。

表2 反射率因子与水深的相关系数
图3还给出了二次多项式和对数二次多项式测深模型的检验情况,表4给出了它们的误差统计,采用的反射率因子分别为TM2、TM3、TM1/TM2、TM1/TM3。TM2的二次多项式测深模型比线性测深模型的误差小,在0~10m水深的平均测深误差由2.00m降低到1.93m,10~25m水深的平均测深误差由4.70m降低到4.30m;TM2的对数二次多项式测深模型比对数测深模型的误差也小,在0~10m水深的平均测深误差由1.97m降低到1.91m,10~ 25m水深的平均测深误差由4.62m减低到4.41m。 TM3、TM1/TM2、TM1/TM3的二次多项式测深模型也比线性测深模型的误差小,它们的对数二次多项式测深模型则比对数测深模型误差小。表4中,在0~10m水深的情况下,TM1/TM3的二次多项式测深模型误差最小,平均绝对误差为1.66m。
表5给出了多元线性、对数测深模型的误差统计,采用了三组反射率因子,第一组为TM2和TM3,第二组为TM1/TM2和TM1/TM3,第三组为TM2、TM3、TM1/TM2、TM1/TM3。表3中,TM2的线性测深模型在0-10m水深的平均测深误差为2.00m,在10~25m水深的平均测深误差为4.70m,TM3的线性测深模型在0~10m水深的平均测深误差为2.01 m,在10~25m水深的平均测深误差为5.11m。表5中,TM2和TM3的二元线性测深模型在0~10 m水深的平均测深误差为1.97 m,在10~25m水深的平均测深误差为4.39m,比它们的线性测深模型误差小。表4和表5对比,TM2和TM3的二元对数测深模型比它们的对数测深模型在0~10m水深的测深误差相差不大,在10~25m水深的测深误差则明显减小。TM1/TM2和TM1/TM3的二元线性测深模型比它们的线性测深模型在0~10m水深的测深误差减小,在10~25m水深的测深误差则没有减小,二元对数测深模型和对数测深模型对比,也有类似特点。TM2、TM3、TM1/ TM2、TM1/TM3组合的四元线性测深模型比它们的线性测深模型在0~10 m水深的测深误差小,在10~25m水深的测深误差相差不大,四元对数测深模型和对数测深模型对比,也有类似特点。表5中,在0~10m水深的情况下,TM2、TM3、TM1/ TM2、TM1/TM3的四元线性测深模型误差最小,平均绝对误差为1.67m。
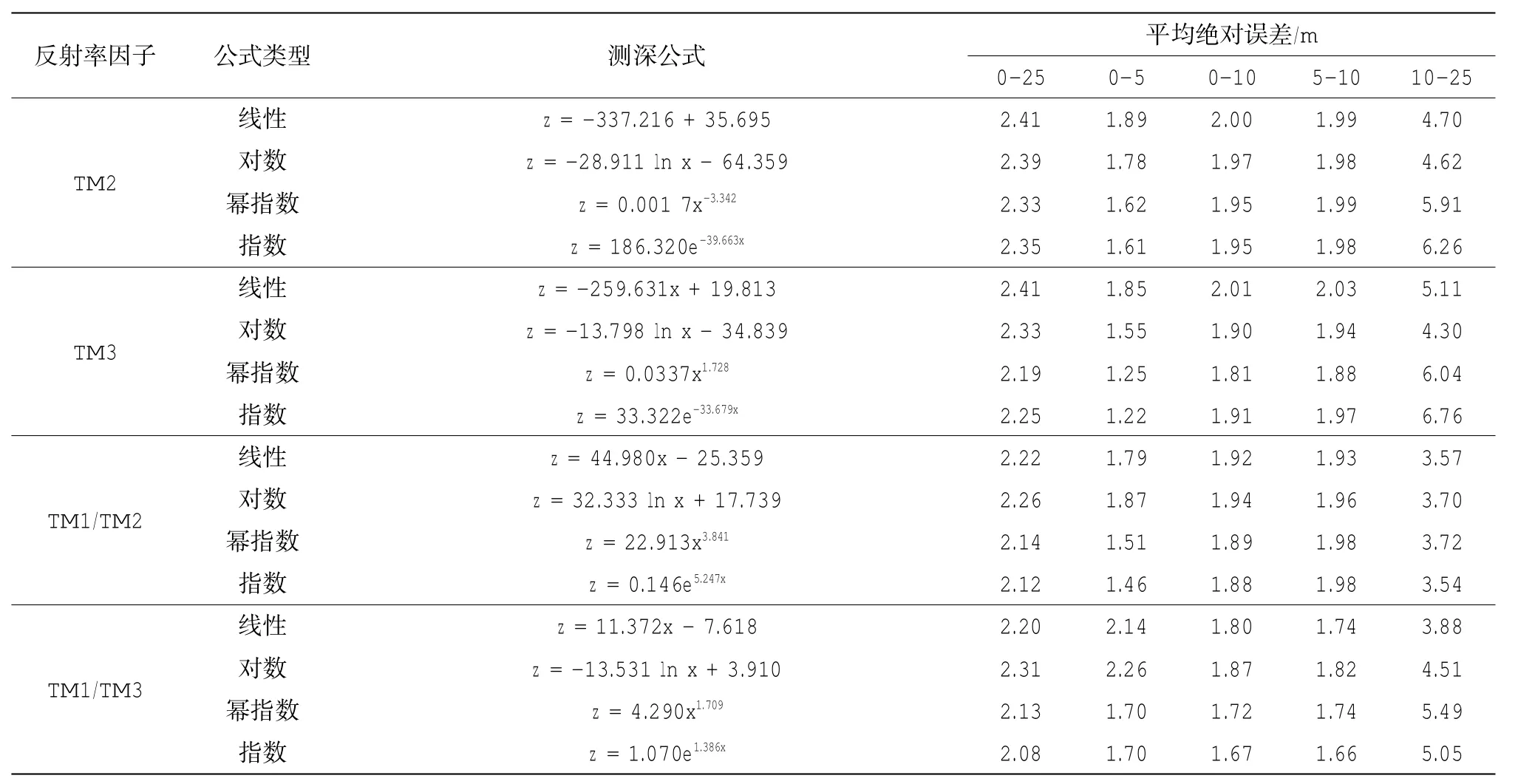
表3 单波段和双波段比值的线性、对数、幂指数、指数测深模型误差统计

图3 单波段和双波段比值的线性、对数、幂指数、指数及多项式测深模型检验

表4 二次多项式测深模型误差统计

表5 多元测深模型误差统计
图3的各种测深模型在10~25m水深区域测深结果普遍偏小,因此采用TM2、TM3、TM1/TM2、TM1/TM3建立了线性、对数、指数、幂指数的分段函数测深模型。表6-9给出了这些测深模型的数学表达式和测深误差统计,图4给出了它们的检验情况。表6-9中表6中x1=0.077 5、 x2=0.082 5,表7中x1=0.037 5、x2=0.042 5,表8 中x1= 0.775、x2= 0.82 5,表9中x1= 1.455、x2= 1.505。表6-9与表3比较,TM2、TM3、TM1/TM2、TM1/TM3的分段函数测深模型误差都比非分段函数测深模型小,不仅在10~25m水深区域的测深误差减小,在0~10m水深区域的测深误差也减小。综合表6-9来看,在0~25 m水深的区域,TM1/ TM3的分段线性测深模型误差最小,图5给出了它反演的整个海域水深,基本给出了水深从外海向海岸逐渐变浅的变化趋势。

表6 TM 2的分段函数测深模型误差统计

表7 TM 3的分段函数测深模型误差统计

表8 TM 1/TM 2的分段函数测深模型误差统计

表9 TM 1/TM 3的分段函数测深模型误差统计

图4 分段函数测深模型检验

图5 TM 1/TM 3线性分段测深模型反演水深
5结论
本文以海口湾为研究区,利用Landsat资料进行可见光遥感测深研究。本文分别采用NDW I、MNDW I、EW I、NW I指数的阈值分割法进行水陆分离,结果表明NDW I指数更适合海口湾,它对水边线反演的平均误差为3.5m。选取与水深相关性比较好的反射率因子TM2、TM3、TM1/TM2、TM1/TM3,采用常见的测深方法,分别建立线性、对数、幂指数、指数测深模型,它们的测深误差在0-10m水深的情况下比较小,其中TM1/TM3的指数测深模型平均绝对误差为1.67m,在实际应用中有参考价值。本文拓展建立了TM2、TM3、TM1/TM2、TM1/TM3的二次多项式测深模型以及对数二次多项式测深模型,还拓展建立这几个反射率因子的二元和四元线性、指数测深模型,从检验情况看,二次多项式测深模型优于线性测深模型,对数二次多项式测深模型优于对数测深模型。本文还建立了这几个反射率因子的分段函数(包括线性、对数、幂指数、指数)测深模型,它们的测深误差都比非分段函数测深模型的误差小。
参考文献
Benny,A H,Dawson,G J,1983.Satellite imageryasan aid tobathymetric Charting in the Red Sea.The Cartographic Journal,20:5-16.
Hengle,W V,Spitzer,D,1991.Multi-temporalwater depth mapping by means of Landsat TM.International Journal of Remote Sensing,12 (4):703-712.
John,M P,Robert,E S,1983.W ater depth mapping from passive remote sensing data under a generalized ratio assumption.Applied Optics,22(8):1134-1135.
McFeeters SK,1996.TheuseofNormalized DifferenceW ater Index(NDW I)in the delineation of open water features.International Journal ofRemote Sensing,17(7):1425-1432.
曹瑞雪,张杰,孟俊敏,2004.利用TM图像数据计算海水深度模型-以双子礁和黄河口水域为例.海洋科学进展.22(z1):65-70.
丁凤,2009.基于新型水体指数(NW I)进行水体信息提取的实验研究.测绘科学,34(4):155-157.
申家双,潘时祥,2002.沿岸水深测量技术方法的探讨.海洋测绘,22(6):60-65.
王艳娇,董文杰,张培群,等,2007.水深可见光遥感方法研究进展.海洋通报,26(5):92-101.
徐涵秋,2005.利用改进的归一化差异水体指数(MNDW I)提取水体信息的研究.遥感学报,9(5):589-595.
闫霈,张友静,张元,等,2007.利用增强型水体指数(EW I)和GIS去噪音技术提取半干旱地区水系信息的研究.遥感应用,2007(6):62-67.
张东,潘雪峰,张鹰,2008.基于可见光遥感测深技术的长江口南支河段河势演变规律研究.海洋学报,30(2):33-37.
朱长明,张新,骆剑承,等,2013.基于样本自动选择与SVM结合的海岸线遥感自动提取.国土资源遥感,25(2):69-74.
(本文编辑:岳心阳)
Study on thewater depth extractionm ethod using visible rem ote sensing in the Haikou Bay
ZHANG Xiao-dong1,2,ZHANG W en-jing3,ZHU Shou-xian2,ZENG W en-hua3
(1.CollegeofHarbor,Coastaland Offshore Engineering,HohaiUniversity,Nanjing210098,China;2.92292 TroopsofPLA,Qingdao 266000,China;3.CollegeofMeteorologyand Oceanography,PLA UniversityofScienceand Technology,Nanjing211101,China)
Abstract:The study ofwater depth extraction methods using visible Landsat remote sensing ismade in the Haikou Bay.Four types ofwater indices,namely NDW I,MNDW I,EW Iand NW I,are used to extract thewaterline from Landsatsensing image,in which NDW Iis proved to be the best.TM2,TM3,TM1/TM2 and TM1/TM3 are checked to have better correlation with the water depth,so they are selected for the water depth extraction models.Based on the familiarmethods,the linear model,the logarithmic model,the power exponentmodel and the exponentialmodel for water depth extraction are made,amongwhich the exponentialmodelusing TM1/TM3 is the bestwith the average absolute errorof1.67m at thewater depth of 0-10m.Furthermore,thequadratic polynomialmodeland the logarithmic quadratic polynomialmodelaremade for thewater depth extraction using TM2,TM3,TM1/TM2 and TM1/TM3 respectively,which are also used to make the binary(or quaternary)linear(or logarithmic)modelsand the segmented functionmodels.It is shown that the quadratic polynomial model is better than the linearmodel,and the logarithmic quadratic polynomialmodel is better than the logarithmicmodel and the segment functionmodel isbetter than thenon-segmented functionmodel.
Keywords:Haikou Bay;visible light;waterdepth extraction from the remote sensing
通讯作者:张文静,电子邮箱:zhangwenjing_lgd@163.com。
作者简介:张晓冬(1986-),男,硕士研究生,主要从事海洋动力学和海洋遥感研究,电子邮箱:zxd8696@163.com。
基金项目:国家自然科学基金(41206163;41076048);中央高校基本科研业务费项目(2011B05714)。
收稿日期:2014-11-02;
修订日期:2015-04-30
Doi:10.11840/j.issn.1001-6392.2016.01.008
中图分类号:P714.3;TP79
文献标识码:A
文章编号:1001-6932(2016)01-0054-10
