潮流泥沙数学模型在青岛港挡沙堤工程的应用

李大鸣，阳　婷，李杨杨，欧阳锡钰

（天津大学　水利工程仿真与安全国家重点实验室，天津　300072）



潮流泥沙数学模型在青岛港挡沙堤工程的应用

李大鸣，阳婷，李杨杨，欧阳锡钰

（天津大学水利工程仿真与安全国家重点实验室，天津300072）

摘要：考虑波浪辐射应力对潮流场和泥沙运动的影响，建立了青岛港前湾三期码头前沿挡沙堤工程二维潮流泥沙数学模型。在采用实测资料验证的基础上，运用模型对本海域在无挡沙堤及不同挡沙堤长的各种方案的流场变化和泥沙回淤情况进行计算研究。结果表明，无挡沙堤时，由于三期工程的建设缩窄了河口至海区的断面面积，断面西侧的浅水区水流速度增大，容易掀起泥沙输移至断面东侧开挖后的深水区，使泥沙在码头前港池中落淤，码头前沿最大淤积强度约为0.818 m/day；而建设挡沙堤后将显著减小码头前沿的泥沙淤积。经过比较，从挡沙堤附近流场与港池航道回淤情况的角度考虑，认为方案二对码头前沿拦沙的效果较好。

关键词：波浪辐射应力；潮流；泥沙；数学模型；挡沙堤；青岛港

近岸水动力环境对海岸带及港工建筑物的影响十分重要，而潮流、波浪和泥沙等相互作用又使得海岸带附近的水动力环境非常复杂。在对其的诸多研究方法中，以数学模型最为方便经济，并成为研究大范围水动力条件变化的主要手段之一（韩亮，2010）。近岸潮流、波浪和泥沙运动规律的基本方程大多都是由偏微分方程来描述的。通过数值计算方法求解这些方程，首先要将这些方程进行离散形成代数方程组，然后在计算机上求解（严恺，2002）。常使用的方法有有限差分法、有限单元法、有限体积法、有限分析法和边界元法等；按差分网格形状的不同可以分为三角形、矩形、四边形、多边形、曲线坐标网格以及不同网格的组合等（张涤明，1991）。

在对近岸水动力环境的大量研究中，河口海岸地区波浪与潮流共同作用下的泥沙运动及其模拟属于前沿课题。早期研究中，Swart（1976）通过将波浪、潮流共同作用下的床面剪切应力替代河流泥沙输运公式中的剪切应力来研究河流输沙问题；David等（1991）采用波流相互作用模型来计算底部切应力，认为在研究泥沙再悬浮及浅水河口床面泥沙运动时考虑波流相互作用是十分重要的。随着相关研究的发展，不少学者采用流场模型，在悬沙扩散方程中采用波流共同作用下的挟沙能力来研究泥沙扩散问题（窦希萍，1992）；窦国仁等（1995）导出了波浪和潮流共同作用下的悬沙输移方程式和挟沙能力公式，建立了河口海岸平面二维泥沙数学模型。另外，也有许多研究者在潮流方程中引入辐射应力（严以新，1988），结合悬沙扩散方程讨论波流共同作用下的泥沙扩散（曹祖德等，1993）；辛文杰（1997）将“波浪辐射应力”、“波流摩阻力”以及“波流挟沙能力”三个要素归纳到水流运动方程和悬沙输送方程中去，建立潮流、波浪综合作用下的河口二维悬沙数学模型。从其他角度出发，白玉川等（2000）根据N-S方程和质量传输方程，采用Reynolds分解法建立了模拟波浪潮流共同输沙及海岸冲淤演变模式；吴永胜等（2002）通过引入紊动封闭方程，耦合波浪和水流之间的相互作用因素，建立了统一描述波浪、水流流场在波浪边界层内、外的变化规律的数学模型。李大鸣等（2014）考虑了波浪场产生的“波浪辐射应力”和“波流挟沙力”动力要素，采用有限元加权质量法建立了波浪作用的潮流泥沙数学模型，对本文有着很大的理论指导意义。

青岛港前湾港区地处山东半岛胶州湾黄岛东南岸线的前湾内，其一﹑二期工程已投入运营。为满足港口货运增长的要求，计划在一﹑二期工程西南面沿岸线，进行三期工程的建设（图1）。随着三期工程向西发展，工程占用了前湾湾顶辛安河口的一部分海区面积，导致河道缩窄；与此同时，三期工程最西侧港池、航道的挖深使得青岛前湾纳潮量增加，港池边坡塌落，浅水区的掀沙随潮流向深水区落淤的泥沙将威胁西侧港池航道的正常水深。为顺利实施青岛港三期工程和减少港池回淤，拟在三期工程最西端建一座挡沙堤，故本文建立波浪潮流泥沙数学模型，对该区的流场动力条件和泥沙回淤情况进行分析研究，为青岛港前湾三期工程的实施及今后港口的建设、维护提供科学依据。

图1　青岛港前湾港区地理位置和模型范围

1数学模型理论

1.1波浪场数学模型

1.1.1基本方程

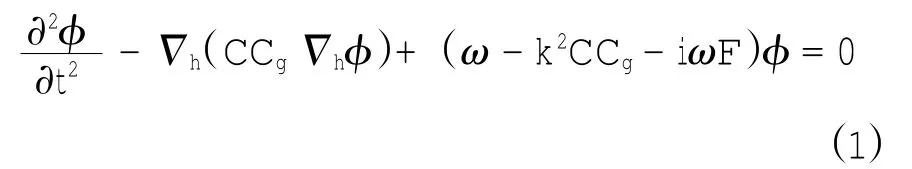
采用三角网格剖分的有限海域折绕射联合计算，并依据波能衰减的缓坡方程（潘军宁等，2001）来确定波浪场：式中：φ表示波势；h=（∂/∂x，∂/∂y）；C表示波速；Cg表示群波速；ω为角频率；k表示波数；F为波能衰减因子；

1.1.2边界条件

入射边界条件：

透、反射边界条件：

式中：γ为反射参数，由下式计算：

式（2）至（6）中，n为入射波向；表示入射波势；φr表示反射波势；R为反射系数；ε为相位差；R =1时为全反射边界，R =0时为全透射边界。

1.2考虑波浪作用的潮流场数学模型

1.2.1基本方程

采用三角网格剖分的有限元加权集中质量法计算潮流场（吴克田，1990）。依据波浪辐射应力作用的二维浅水环流方程：

其中：u、v为流速在x、y方向的分量；z为水位；g为重力加速度；c为谢才阻力系数；h为水深；f为柯氏力系数；S为辐射应力；AH为水平涡粘系数；H为波高；k为波数；ρ为水体密度；α为波向角。

1.2.2边界条件

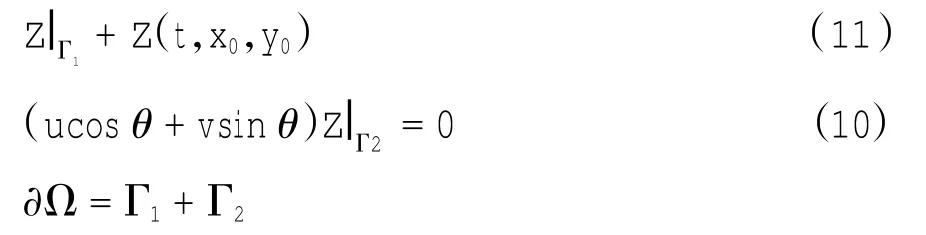
式中：Z为（x0，y0）点上的潮位过程；Γ1为模型水域水线边界；θ为模型陆边界法向角；Γ2为模型水域陆线边界；Ω为平面计算域。

1.3泥沙场数学模型

依据以下方程采用三角网格剖分的三角差分方法计算悬沙含沙量、底沙量和海床变化。

1.3.1考虑紊动水动力影响的泥沙扩散方程（王尚毅，1990）

其中：Cs为悬沙平均含沙量；Cb为床面层内部底沙含沙量；εx、εy为x、y方向的扩散系数；ωs为悬沙平均沉速；d50s为悬沙中值粒径；As为与悬沙平均沉速和中值粒径相关的修正系数。

1.3.2考虑两相流相互作用的底沙输移的连续和运动方程

其中：ωb为底沙平均沉速；d50b为底沙中值粒径；Ab为与底沙平均沉速和中值粒径相关的修正系数；v为水流运动粘性系数；ks为广义渗透率。

1.3.3床面变形方程

其中：γc为底沙干容重；γs为悬沙容重；CA为全沙含沙量。（注：以上平均含沙量均采用含沙相对体积比）。

1.3.4边界条件

模型水域水线边界Γ1处网格节点的含沙量以平衡挟沙理论（曹志先，1997）为基础，根据该边界处的水动力条件及附近海域的泥沙中值粒径计算确定；而模型水域陆线边界Γ2处网格节点的含沙量始终为0，即：

海床底部变化边界条件由（16）式确定。

2模型布置

青岛港前湾港区潮流泥沙数学模型的模型范围如图1所示，东起团岛鼻与脚子石嘴一线海域，西至辛安河口西岸线（120°17＇24＂E-120°10＇24＂E），东西最大宽度约10.5 km；南起海西湾湾顶，北到团岛嘴与黄岛东岸一线海域（35°58＇N-36°3＇30＂N），模型长约10.5 km。模型覆盖海域面积达60 km2。模型中部采用规则的有限元三角形单元进行剖分，边界则采用不规则三角形网格使工程和岸线与单元网格完全拟合。验证模型以三期工程建设前的地形数据为基础，空间步长约为160m，平面剖分网格见图2左部分。为较准确的描述前湾港区三期工程西端挡沙堤对浅滩泥沙的拦挡作用，计算模型采用如图2右部分所示的平面剖分网格，在三期工程附近的浅滩和港区周边取1.6 km×8 km的矩形加密区，空间最小步长约为25m。对不同长度的挡沙堤，模型平面剖分网格略有差别，剖分网格图略。

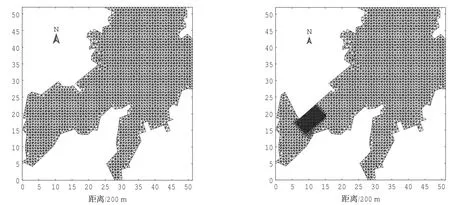
图2　验证模型剖分网格（左）及挡沙堤建设前模型加密网格（右）图

3模型验证

3.1观测站潮流验证

模型验证计算采用2001年6月5日8时-6日9时大潮过程、6月10日8时-11日9时中潮过程和6月17日9时-18日10时小潮过程对模型中四个验潮站进行了验证，验潮站分别为L1、L2、L3 和L4，位置如图3所示。通过对四点全潮逐时的潮位、流速、流向验证资料进行调试验证，可以看到各点潮位吻合良好，流速、流向趋势基本一致。限于篇幅，这里只给出各测点大潮潮位、流速、流向逐时过程验证结果，见图4。

图3　验潮站位置示意图

3.2潮流场验证

模型还分别验证了整个模型区域在大、中、小潮过程的涨落潮流场。这里只给出大潮过程的涨落潮流场图，见图5。从图中可以看出，涨潮主流由外海经湾口流入，一股强流向北流入胶州湾，一股较弱的分流流向西南的前湾，向南流入海西湾的水流流量最小；落潮分别由胶州湾、前湾和海西湾汇流后流向外海，流态与实际观测基本一致。

图4　大潮潮位、流速、水位过程验证

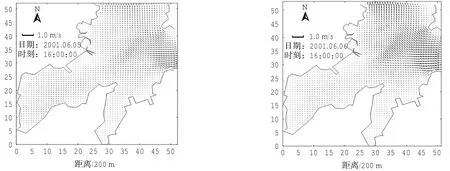
图5　验证模型大潮落潮（左）、涨潮（右）流场图

3.3观测站含沙量验证

含沙量的验证计算采用中、大、小潮同期资料。其中各个测点大潮验证结果见图6，与实测过程基本一致；整个模型区域大潮落、涨急情况的含沙量分布见图7，可见含沙量分布基本合理，模型基本能反映原型的物理特征。

图6　大潮含沙量过程验证

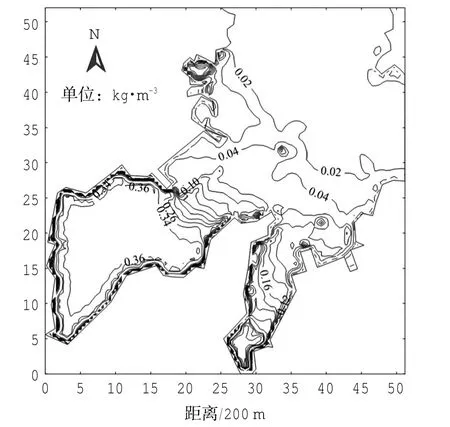
图7　模型验证大潮含沙量分布图

4挡沙堤方案计算

4.1挡沙堤布置方案

青岛港前湾港区三期工程拟建的挡沙堤由码头前沿向东南延伸。为比较不同长度挡沙堤的拦沙效果，分别设计长度为180m、200m和220m，将这三种情况分别称为第一、第二和第三方案，未建挡沙堤前的情况称为工程前方案。为比较各方案挡沙堤附近流场与港池航道回淤情况，在挡沙堤拟建位置附近沿三期工程泊位岸线，选择5个特征点，用于定量比较工程前后主要物理量的变化，特征点距挡沙堤距离分别为0.0m、100m、200m、300m 和400m。挡沙堤及各个特征点位置如图8所示。

图8　挡沙堤附近特征点位置示意图

4.2各方案计算

4.2.1潮流场计算

考虑上述四种方案下对模型区域在大、中、小潮的涨落潮进行潮流场计算。其中，在青岛港前湾港区三期工程建设完成、港池航道开挖后无挡沙堤情况下的工程前方案中，由于工程占用海区，三期工程西端形成河口到海区缩窄断面，断面西侧为浅水区，水流速度较大，断面东侧为开挖后的深水区，水流速度较小，形成了一个大小流速交换区，如图9左边部分所示的大潮落潮过程。而挡沙堤工程建设后，缩窄断面处继续缩窄，使浅水区与深水区缩窄断面离开码头前沿，大流速与小流速交换区离开码头前沿。工程第二方案，即挡沙堤为200m时，三期工程附近大潮期落潮流场如图9右部分所示；第一和第三方案潮流场与第二方案相似，不再以图形方式给出。表1给出各方案特征点上大潮落潮的极值情况。

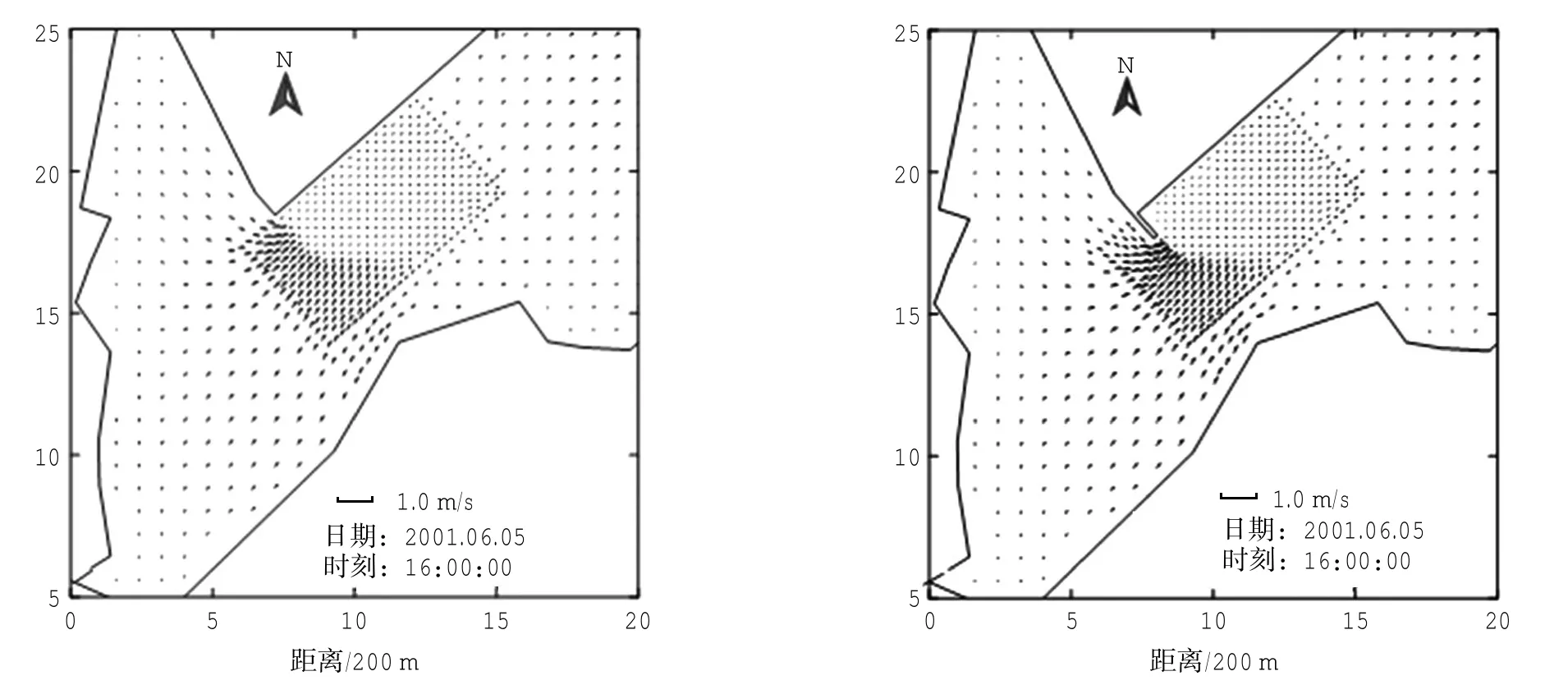
图9　挡沙堤工程前（左）及第二方案（右）大潮落潮流场

表1　各方案特征点大潮落潮流速极值

4.2.2日淤积强度计算

从上述潮流场的计算可以看出，三期工程西端形成的河口到海区缩窄断面西侧为水流速度较大的浅水区，容易带动浅水区掀起的泥沙随水流运动；断面东侧为水流速度较小的开挖后深水区，泥沙不容易起动，水流挟沙能力较弱；在落潮流作用下，浅水区泥沙随水流经缩窄断面进入开挖后的深水区，水流挟沙能力迅速减弱，大部分泥沙快速沉积，少部分泥沙向前湾口方向扩散，但在涨潮流作用下，少部分泥沙的一部分会随水流作用回到缩窄断面或挡沙堤东侧落淤，增加了断面处深水侧的淤积厚度。根据潮流场计算结果得到开挖完成后各方案大、中、小潮作用24 h后的含沙量分布与港池航道淤积图，以第二方案大潮过程淤积情况及含沙量分布为例，如图10所示；各方案特征点上大潮24 h累积淤积量以表2给出。

表2　大潮不同方案挡沙堤东侧不同部位日淤积强度

从以上图表中可以看出，不加挡沙堤的工程前方案，码头前沿在大潮情况下淤积强度最大，最大淤积强度发生在浅水区与深水开挖区的交界断面处，最大数值为0.818m/day；建设挡沙堤后码头前沿淤积厚度减小，最大淤积强度仍发生在大潮情况下，淤积部位为挡沙堤东侧堤脚，第一方案挡沙堤长度为180m时，大潮最大淤积强度为0.222m/day；第二方案挡沙堤长度为200m时，大潮最大淤积强度为0.090 m/day；第三方案挡沙堤长度为220 m时，大潮最大淤积强度为0.172m/day，第二方案挡沙堤拦沙作用最明显，可将码头前沿的最大淤积强度减少约89％。

图10　挡沙堤工程第二方案大潮淤积分布（左）及含沙量分布（右）

4.2.3泥沙年淤积强度计算

青岛港前湾港区三期工程建设完成、港池航道开挖后，初期会由于边坡塌落和浅滩来沙出现较高强度的回淤，但随着回淤厚度的增加回淤强度会逐渐减弱。考虑大、中、小潮作用，模拟港池航道开挖后一年回淤情况，如表3所示，比较工程前方案与挡沙堤第二方案特征点上的年淤积强度，工程前方案与挡沙堤第二方案年淤积强度分布见图11。

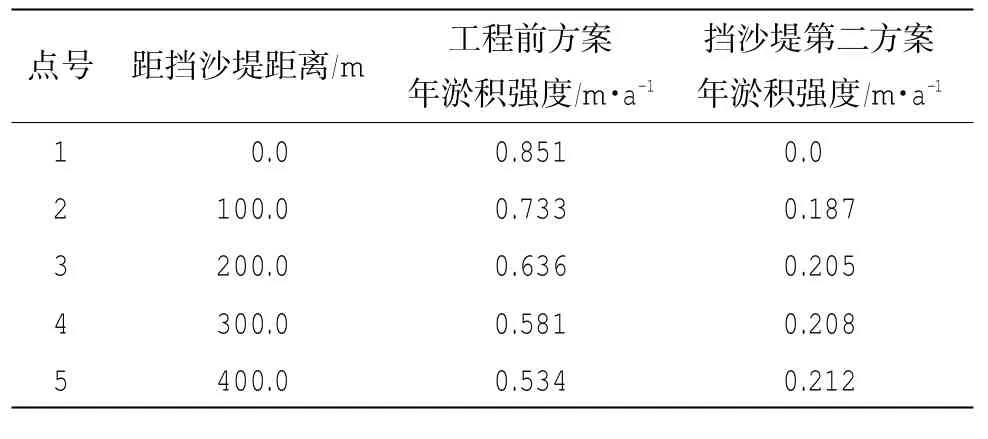
表3　第二方案与工程前方案年淤积强度比较

图11　挡沙堤工程前（左）及第二方案（右）年淤积强度分布

从图表中可以看出，建设挡沙堤主要对三期工程西侧，有明显的减淤效果。在表3中，特征点上工程前年最大淤积强度为0.851m/a；建设200m挡沙堤后，码头前沿的年最大淤积强度为0.212m/a，最大淤积强度位于第5特征点处，与工程前方案相比约减少75％。通过对比表2和表3可以发现，工程第二方案最大日淤积强度与最大年淤积强度位置不同，前者在第2点位处最大而第5点位处最小，后者则相反；因为前者计算的是港池开挖后某一特征潮作用下24 h内的淤积高度，而后者计算的是全年的淤积高度。港池开挖后，在一次大潮、中潮或小潮独立作用的时间内，泥沙会在开挖后港池边缘挡沙堤堤头处的地方先落淤，受此时淤积带的影响，挡沙堤东侧第2点位处淤积强度相对较大，而此时第5点位处还未受到淤积带影响；而在全年潮流的作用下，港池内泥沙淤积带向第五点位方向发展，最大淤积强度点也向港池东侧推移。从图11中还可以看出挡沙堤能够引起三期工程港池航道内淤积分布的改变，但港池航道整体的淤积总量变化不大，泥沙淤积空间分布也逐渐趋于均匀。

5结论

本文建立了考虑波浪作用的二维潮流数学模拟计算模型，并使用实测海流资料验证所建立的潮流数学模型的合理性。通过对挡沙堤工程各方案进行典型潮的模拟潮流计算，分析工程和流态的相互影响，并从挡沙堤工程布置方案上对流场变化、泥沙淤积和运移角度加以分析，得到以下结论：（1）青岛港前湾港区三期工程建设完成、港池航道开挖后，在无挡沙堤的工程前方案中，码头前沿在大潮情况下淤积强度最大，最大数值为0.818 m/day。（2）青岛港前湾港区三期工程建设200m挡沙堤时，对码头前沿拦沙效果最好，大潮时码头前沿最大淤积强度减少为0.090m/day，比未建设挡沙堤的情况，码头前沿的最大淤积强度减少约89 ％，挡沙堤对减小三期工程码头前沿淤积的作用明显。（3）建设200m挡沙堤后，码头前沿的年最大淤积强度为0.212m/a，约减少75％，挡沙堤对减小三期工程码头前沿年淤积强度的作用也较明显。

参考文献

Schoellhamer David H,Levesque Victor A,1991.W ind generated wave resuspension of sediment in Old Tampa Bay.Proceedings-National Conferenceon Hydraulic Engineering,(29):85-90.

Swart D H,1976.Coastal sediment transport.Computation of Longshore Transport,ReportR968.

白玉川，顾元棪，蒋昌波，2000.潮流波浪联合输沙及海床冲淤演变的理论体系与其数学模拟.海洋与湖沼，31（2）：186-196.

曹志先，1997.泥沙数学模型近底边界条件I：平衡输沙.水利学报，（1）：11-19.

曹祖德，王桂芬，1993.波浪掀沙、潮流输沙的数值模拟.海洋学报，15（1）：107-118.

窦国仁，董凤舞，窦希萍，李禔来，1995.河口海岸泥沙数学模型研究.中国科学，25（9）：995-1001.

窦希萍，罗肇森，1992.波浪潮流共同作用下的二维泥沙数学模型.水利水运科学研究，（4）：331-338.

韩亮，2010.二维潮流波浪数学模型及工程应用.天津大学.

李大鸣，欧阳锡钰，潘番，等，2014.考虑波浪辐射应力的潮流泥沙数学模型.海洋通报，33（6）：703-711.

潘军宁，左其华，洪广文，2001.一种推广的缓坡方程.海洋工程，19（1）：24-31.

王尚毅，顾元蒳，郭传镇，1990.河口工程泥沙数学模型.海洋出版社，120-192.

吴克田，1990.二维浅水波问题Galerkin解法的质量集中法.计算物理，7（1）：1-6.

吴永胜，练继建，王兆印，等，2002.波浪-水流相互作用模型.水利学报，（4）：13-17.

辛文杰，1997.潮流、波浪综合作用下河口二维悬沙数学模型.海洋工程，15（1）：30-47.

严恺，2002.海岸工程.海洋出版社，622-625.

严以新，1988.潮汐河口地区波流相互作用的数学模型.海洋工程，7（3）：47-56.

张涤明，1991.计算流体力学.中山大学出版社，181-187.

（本文编辑：岳心阳）

App lication of thenum ericalm odelof tidal currentsand sedim ents in the dike engineering of Qingdao Port

LIDa-ming,YANG Ting,LIYang-yang,OUYANG Xi-yu
（State Key LaboratoryofHydraulic EngineeringSimulation and Safety,Tianjin University,Tianjin 300072,China）

Abstract：In this paper,a 2-D tidal currentand sedimentnumericalmodel for the dike engineering at the former bay of Qingdao Port Phase 3 is established in view of＂wave radiation stress＂generated by the wave field on the flow field and sedimentmovement.Based on the observed data,themodel isapplied to study the change of currentsand back silting in the portareawithout the dike and with the dike of different length.The results show thatwhen there is no dike here,the cross section area between the estuary and sea narrows due to the construction of the Phase 3,and itcauses the increasing ofwater flow rate at the shallow water on the west side of cross section,which makes sediments transport from the west to the east deepwater side easilywith the sedimentation in theharborbasin.In this case,themaximum silting intensity ofwharfapron is about0.818m/day.W hereas the dikebuildingwillsignificantly reduce the sedimentation of thewharfapron.According to the comparison,case2 isbetter in view of the sedimentdeduction.

Keywords：wave radiation stress;tidalcurrents;sediments;numericalmodeling;dike;Qingdao Port

通讯作者：阳婷，硕士研究。电子邮箱：544052703@qq.com。

作者简介：李大鸣（1957-），男，博士，教授，主要从事水力学与河流动力学研究工作。电子邮箱：lidaming@tju.edu.cn。

收稿日期：2014-12-29；

修订日期：2015-04-30

Doi：10.11840/j.issn.1001-6392.2016.01.014

中图分类号：TV148

文献标识码：A

文章编号：1001-6932（2016）01-0103-09