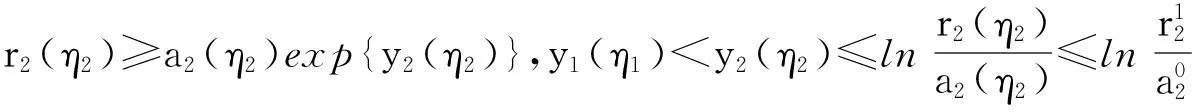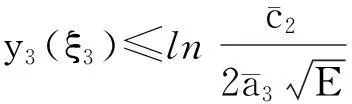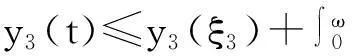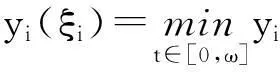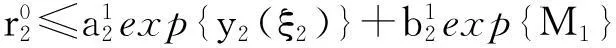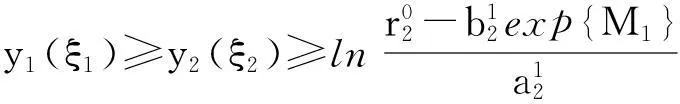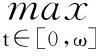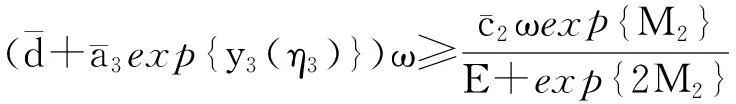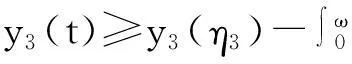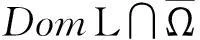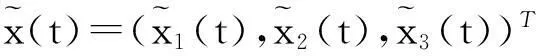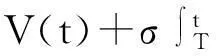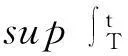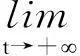一类具有非单调型功能反应的捕食-食饵扩散系统的持久性和全局吸引性

徐长玲，程荣福

(北华大学数学与统计学院，吉林 吉林　132013)



一类具有非单调型功能反应的捕食-食饵扩散系统的持久性和全局吸引性

徐长玲，程荣福

(北华大学数学与统计学院，吉林 吉林132013)

摘要：利用微分方程的比较原理和重合度理论中的延拓定理，及Lyapunov函数和Barbalat引理，研究了一类具有双密度制约和非单调型功能性反应的捕食-食饵扩散系统的持久性和全局吸引性，获得了周期系统存在唯一全局渐近稳定正周期解的充分条件.

关键词：扩散系统；正周期解；非单调功能性反应；持久性；全局渐近稳定性

【引用格式】徐长玲，程荣福.一类具有非单调型功能反应的捕食-食饵扩散系统的持久性和全局吸引性[J].北华大学学报(自然科学版)，2016，17(2)：141-147.

1引言

捕食者和被捕食者系统是生态数学中非常经典的模型，现已有大量的研究工作[1-8]，对于具有双密度制约和非单调型功能反应的捕食者与被捕食者模型已成为研究热点之一.本文进一步考虑如下系统

(1)

其中：gi(xi，t)=ri(t)-ai(t)xi(t)(i=1，2)，x1(t)，x2(t)分别表示食饵在第1阶段和第2阶段中时刻t的密度；D1(t)和D2(t)分别表示扩散系数；x3(t)是捕食者在第1阶段中时刻t的密度；ri(t)，ai(t)，bi(t)，ci(t)，d(t)，Di(t)，a3(t)∈C(，+)(i=1，2)，当t∈+=(0，+)时，它们是连续有界严格正的函数；时滞τ1>0，τ2>0，E>0；Ki(s)：+→+是分段连续函数且满足(i=1，2).系统(1)的生态意义参见文献[1].

φi∈C+，xi(s)=φi(s)≥0， s∈[-τ，0]， φi(0)>0， i=1，2，3.

(2)

2系统的持久性

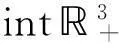
证明类似于文献[2-3]，略.

为了证明系统的一致持久性，不妨假设(x1(t)，x2(t)，x3(t))T是系统(1)的满足正初始条件(2)的任意正解，设 V1(t)=max{x1(t)，x2(t)}，计算系统(1)的右导数，得

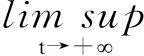
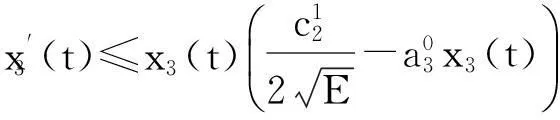
设V2(t)=min{x1(t)，x2(t)}，类似地，当t≥T2时，从系统(1)，有

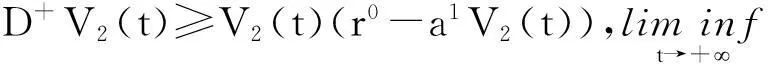
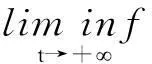
设T=T4，M=max{M1，M2}，m=min{m1，m2}.综上，任意正解Mi，mi(i=1，2)存在，且它们不依赖系统(1)，那么，我们得到紧区域：

当t>T时，系统(1)的解将进入并保留在紧区域D内，因此D是正向不变集且是系统(1)的最终有界域.据此，可以直接得到下面引理：

引理2如果

成立，那么系统(1)是一致持久的.

3系统正周期解的存在性

假设ri(t)，ai(t)，bi(t)，ci(t)，d(t)，Di(t)，a3(t)∈C(，+)(i=1，2)是关于周期ω的正周期函数，系统(1)是ω-周期系统.在下面定理证明中将利用Mawhin和Gaines的持续性定理[4].

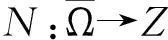
(a)Ly≠λNy，∀y∈∂Ω∩DomL，λ∈(0，1)；

(b)QNy≠0，y∈∂Ω∩KerL；

(c)deg{JQN，Ω∩KerL，0}≠0.

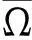
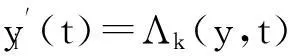
(3)

D2(t)exp{y1(t)-y2(t)}，

取X=Z={(y1(t)，y2(t)，y3(t))T∈C(，3)：y(t+ω)=y(t)}，且yyi(t)，y∈X.那么X和Z是在此范数下的Banach空间，利用周期性，易知Λi(y，t)是ω-周期函数.令 Nx=(Λ1(y，t)，Λ2(y，t)，Λ3(y，t))T，y∈X.；，则

是Z中的闭子集，且

KerL=3，dimKerL=3，

故L是指标为零的Fredholm映射.容易证明P，Q 是连续投影且使得

ImP=KerL，KerQ=ImL=Im(I-Q).

因此L的逆映射KP有形式KP：ImL→DomL∩KerP，且

于是

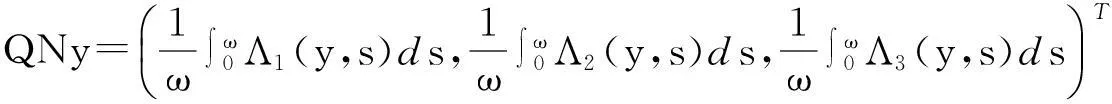
KP(I-Q)Ny=(ψ1(y，t)，ψ2(y，t)，ψ3(y，t))T，

对应算子方程 Lx=λNx，λ∈(0，1)，有

(4)

假设y(t)∈X是系统(4)对应于某个λ∈(0，1)的ω-周期解，于是存在η1，η2∈[0，ω]，使得

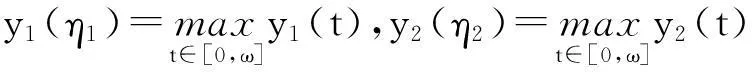
进而

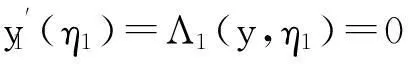
(5)

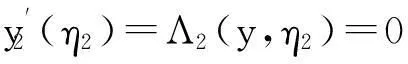
(6)

如果y1(η1)≥y2(η2)，那么y1(η1)≥y2(η1)，利用式(5)有

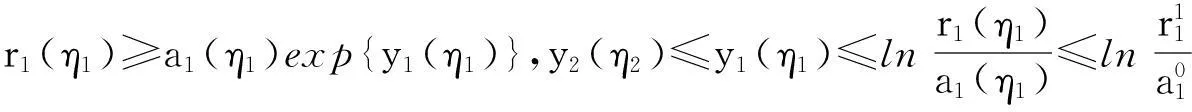
(7)

如果y1(η1)

(8)

因此，对任意t∈[0，ω]有

(9)

将系统(4)的第3个等式两边从0到ω积分，有

(10)

利用式(10)，进而有

(11)

(12)

那么，对于任意t∈[0，ω]，利用式(11)和(12)有

(13)

(14)

(15)

如果y1(ξ1)≥y2(ξ2)，那么y1(ξ2)≥y2(ξ2)，利用式(15)和(9)有

(16)

如果y1(ξ1)

那么，对任意t∈[0，ω]有

(17)

利用式(9)和(17)有

(18)

利用式(10)和(17)有

(19)

利用式(11)和(19)，对任意t∈[0，ω]有

(20)

从式(13)和(20)有

(21)

因此，从式(18)和(21)有

(22)

考虑如下方程

(23)

其中y=(y1，y2，y3)T∈3，μ∈[0，1].对系统(23)的任意解，存在0<ρ0<+，使得

(24)

易见，ρ1，ρ2，ρ0不依赖参数λ.

令B=2ρ2+ρ1+ρ0，且

那么Ω满足引理3的条件(a).

当y∈∂Ω∩KerL=∂Ω∩3时，从式(23)和(24)，有QNy≠0.因此，满足引理3的条件(b).

为简单起见考虑F1=0，F2=0，F3=0.定义映射φ：DomL∩KerL×[0，1]→X如下：

φ(y，μ)=(F1，F2，F3)T，φ(y，μ)=(F1，F2，F3)T.

当(y1，y2，y3)T∈∂Ω∩3，μ∈[0，1]时，利用式(23)和(24)，得φ(y，μ)≠0.注意ImP=KerL，令J是恒等映射，直接计算有

定理1如果

那么系统(1)至少有一个正ω-周期解.

4系统的全局吸引性

引理4[5](Barbalat 引理)假设f是定义在[t0，+)上的非负可积的一致连续函数，其中t0≥0，那么成立.

定理2系统(1)满足正初始条件(2)和引理2、定理1的条件，如果

成立，那么系统(1)有唯一全局吸引性正解.

其中

计算系统(1)的解V(t)的右导数，得到

设0<σ=min{σ1，σ2，σ3}，那么

将上式从T到t积分，有

因此

证毕.

参考文献：

[1] F Y Wei，S H Wang.Periodicity of nonautonomous competitive systems with infinite delay and diffusion[J].Journal of Biomathematics，2012，27：193-202.

[2] Y M Huang.Global stability for a diffusive model with time delay and functional response[J].Journal of Biomathematics，2006，21：370-376.

[3] G Z Zing，J F Chen.Persistence and periodic orbits for two-species non autonomous diffusion models[J].Math Comput Modeling，1994，20：69-80.

[4] R E Gaines，J I Mawhin.Coincidence degree and nonlinear differential equations[M].Berlin：Springer-Verlag，1997：40-45.

[5] I Barbalat.System dequation differentilles doscilltion nonlinears[J].Rev Math Pure and Appl，1959，4：267-270.

[6] A Rojas-Palma，E Gonzalez-Olivares.Optimal harvesting in a predator-prey model with Allee effect and sigmoid functional response[J].Appl Math Model，2012，36：1864-1874.

[7] P Yangzhen，L Changguo，F Shunhou.A mathematical model of a three species prey-predator system with impulsive control and Holling functional response[J].Math Com Appl，2013，219：10945-10955.

[8] M Javidi，N Nyamoradi.Dynamic analysis of a fractional order prey-predator interation with harvesting[J].Appl Math Mode，2013，37：8946-8956.

【责任编辑：伍林】

Persistence and Global Attractivity of a Class of Predator-Prey Diffusive System with Non-Monotonic Type Functional Response

Xu Changling，Cheng Rongfu

(MathematicsandStatisticsSchoolofBeihuaUniversity，Jilin132013，China)

Abstract：We investigate the persistence and global attractivity of a class of predator-prey diffusive system with double density restrict and non-monotonic type functional response by applying Comparison Theorem of differential equation，the Continuation Theorem of coincidence degree theory，Barbalat Lemma and Lyapunov Function.The sufficient conditions with the existence of the unique globally asymptotically stable of the positive periodic solution are obtained.

Key words：diffusive system；positive periodic solution；non-monotonic type functional response；persistence；global asymptotic stability

中图分类号：O175.7

文献标志码：A

作者简介：徐长玲(1982-)，女，硕士，讲师，主要从事微分方程定性理论研究，E-mail：xcl19820106@163.com.

基金项目：国家自然科学基金项目(11201008).

收稿日期：2016-01-08

文章编号：1009-4822(2016)02-0141-07

DOI：10.11713/j.issn.1009-4822.2016.02.001