冷却猪肉阴性样品中气单胞菌概率分布的影响与优选

董庆利，宋筱瑜，丁　甜，刘　箐

(1. 上海理工大学医疗器械与食品学院，上海200093； 2. 国家食品安全风险评估中心，北京100021；

3. 浙江大学 生物系统工程与食品科学学院，浙江杭州310058)



冷却猪肉阴性样品中气单胞菌概率分布的影响与优选

董庆利1，宋筱瑜2，丁甜3，刘箐1

(1. 上海理工大学医疗器械与食品学院，上海200093； 2. 国家食品安全风险评估中心，北京100021；

3. 浙江大学 生物系统工程与食品科学学院，浙江杭州310058)

摘要：探讨不同阴性样品中致病菌污染水平对定量风险评估结果的影响。以冷却猪肉中气单胞菌定量暴露评估为例，设定阴性样品中致病菌为零值和最大值(检测限)2种极端场景，由此预测冷却猪肉中因气单胞菌导致食物中毒的概率分别为33.6%和69.3%，显著高于根据Jarvis经典公式模拟阴性样品的结果(22.1%，P<0.01)。同时，应用赤池信息量准则(AIC)、贝叶斯信息准则(BIC)和卡方检验(X2)等评价参数，对阴性样品污染水平的不同连续型概率分布进行了比较，表明上述两种极端场景下应用指数分布最优，AIC分别为-41.24和-135.62，低于逻辑、正态、三角、均匀分布等结果，但与离散型概率分布预测食物中毒概率的差异不显著。建议今后的微生物定量风险评估研究中，必须考虑阴性样品中致病菌的存在，并应选择合适的概率分布用以描述阴性样品中致病菌的污染水平。

关键词：阴性样品；气单胞菌；概率分布；风险评估

微生物定量风险评估(quantitative m￣i￣c￣r￣o￣b￣i￣o￣l￣o￣g￣i￣c￣a￣l risk assessment,QMRA)可用于评估特定致病菌对人群健康(发病率或爆发率)的定量影响[1]。QMRA包括4个步骤：危害识别、危害特征描述、暴露评估和风险特征描述。其中，暴露评估是微生物定量风险评估的研究核心。在已完成的定量暴露评估研究中，冷却猪肉中的气单胞菌[2]、即食凉拌菜中的单增李斯特菌[3]和蒸煮米饭中的蜡样芽胞杆菌[4]等样品，受检测方法所限，初始污染水平高于检测限的样品认定为阳性样品，如冷却猪肉中气单胞菌为0.78 lg(CFU/g)；相应地，低于此检测限的认定为阴性样品。为使QMRA研究中的致病菌初始污染水平更能接近实际，研究中常假定阴性样品的污染水平分布以Jarvis的经典公式推测，并用反向偏斜累积均匀分布(Uniform)描述阴性样品中的致病菌浓度[2-4]。但这种方法和致病菌的实际分布有较大差距，如冷却猪肉中气单胞菌的阴性结果得到最小值、平均值和最大值分别为-5.22、-2.22和0.78 lg(CFU/g)[2]，意为低于检测限的阴性样品中致病菌实际数量出现概率一致，这与一般微生物在食品中随机分布的常识不符，因此得到的暴露评估结果可靠性有待商榷。

提高QMRA评估结果可靠性的最根本方法之一是提高微生物检测方法的精度，由此得到致病菌的真实分布，作为评估的输入值，得到风险评估结果为风险管理和交流提供理论基础[5]。另外，在现有研究水平上，不同阴性样品分布的假设，必定对QMRA的结果产生较大影响，量化这种影响有待于明确。

本研究中，笔者以冷却猪肉中气单胞菌定量评估为例[2]，首先分析不同阴性样品污染水平的假设(包括为零值和检测限值2种极端场景)对定量暴露评估结果的影响，特别是导致不同的食物中毒概率比较；分析不同阴性样品污染水平应用不同连续型概率分布(贝塔、指数、伽马、逻辑和正态等)的差异，并通过不同评价参数比较确定最优分布，进而比较离散型和连续型概率分布对致病菌最终污染水平的差异，由此为今后微生物风险评估研究考虑阴性样品的定量影响提供理论参考。

1数据来源与分析方法

1.1数据来源

本研究引用气单胞菌的相关数据来源于文献[2]中的定量暴露评估，为某市2009—2010 年以随机抽样的方式从超市中采集冷却猪肉共计100份样品，按国标法进行检测后的结果，近似认为是冷却猪肉中气单胞菌的初始污染量。

1.2场景设定及概率分布模拟

设定以下5种场景，分别描述如下。

场景1(S1)：冷却猪肉中阴性样品(Ln)的气单胞菌以Jarvis公式分布，即符合累计概率分布Cumulative (-5.22,0.78,{-5.22,-2.22,0.78},{0.01,0.50,0.99})，阳性样品(Lp)分布代表的污染率(Pp)同文献[2]，冷却猪肉的初始污染水平仍按综合阳性和阴性样品的离散概率分布Discrete (Lp:Ln,Pp:(1-Pp))设定。

场景2(S2)：冷却猪肉中全部阴性样品的气单胞菌设定为0，初始污染不分阳性和阴性，按离散概率分布Discrete (0,4,{0,0.78,1.00,1.33,1.60,1.85,2.33,2.41,2.48,2.59,2.71,3.26,3.36},{0.86,0.01,0.02,0.01,0.01,0.01,0.02,0.01,0.01,0.01,0.01,0.01,0.01})设定。此场景假设低于检测限的阴性样品中实际没有致病菌的极端情况。

场景3(S3)：冷却猪肉中全部阴性样品的气单胞菌污染水平设定为0.78 lg(CFU/g)，即最大值或检测限值，初始污染不分阳性和阴性，按离散概率分布Discrete (0,4,{0.78,1.00,1.33,1.60,1.85,2.33,2.41,2.48,2.59,2.71,3.26,3.36},{0.87,0.02,0.01,0.01,0.01,0.02,0.01,0.01,0.01,0.01,0.01,0.01})设定。此场景假设低于检测限的阴性样品中实际全部在检测限值的极端情况。

场景4(S4)：对S2按常见的连续型概率分布函数分别拟合，如表1所示。

场景5(S5)：对S3按常见的连续型概率分布函数分别拟合，如表1所示。

进而采用蒙特卡罗(Monte Carlo)模拟方法，运用@RISK 6.0风险评估软件(美国Palisade公司)对上述不同场景的设定参数进行模拟分析，迭代10 000次后比较不同气单胞菌最终污染水平对应的累积概率。以气单胞菌5 lg(CFU/g)为导致食物中毒的风险阈值[2]，计算S1、S2和S3场景对应的超过风险阈值的概率。

表1　常用连续概率分布函数表达式

1.3概率分布的评价参数

应用@RISK软件中RiskFit 函数对S4和S5场景按常见概率分布分别拟合，选择3个评价参数如下[5-6]：

赤池信息量准则AIC=2k1-2lnL

(1)

贝叶斯信息准则BIC=k2lnn-2lnL

(2)

式中：L是似然函数，k1和k2分别是拟合的估计参数数量，n是样本数。

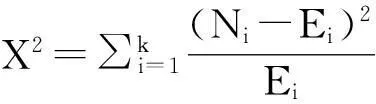
(3)

式中：k为将x轴分成数据段的个数，Ni为第i个数据段中观测的样本数，Ei为第i个数据段中期望的样本数。

2结果与讨论

2.1不同场景的阴性样品污染水平的概率模拟

对设定的3种场景S1、S2和S3分别通过@RISK软件模拟分析，求得最终的气单胞菌菌数的累积概率分布，结果如图1所示。由计算得知，S1、S2和S3场景下超过5 lg(CFU/g)的概率分别为22.1%、33.6%和69.3%，三者之间差异显著(P<0.01)。图1表明设定的阴性样品中气单胞菌值越高，越接近检测限(如S3将所有阴性样品设定为0.78 lg(CFU/g))，估计的超过风险阈值的概率越高，导致食物中毒的可能性越高，这与预想一致。

图1　　　阴性样品污染水平对气单胞菌定量　　　暴露评估的影响Fig.1　　　Effects of pathogen distribution in negative sample　　　on the quantitative exposure assessment of　　　Aeromonas spp.

2.2不同阴性样品概率分布的评价比较

对设定的2种场景S4和S5按照常见的连续型概率分布函数分别拟合，并通过计算AIC、BIC和X2等参数进行评价，结果如表2 所示。其中Beta、Gamma和Pert分布无法收敛，未列在表2中。

从表2可知：对同一场景，AIC和BIC的结果非常相近，两者的理论基础均依赖于贝叶斯分析，是从贝叶斯先验概率的不同假设得出的2种不同形式，如式(1)和(2)所示。AIC和BIC都属于“信息标准”检验，专门设计用于模型选择。AIC和BIC实际值并非代表特定拟合的绝对优度，所以只有比较才有意义[7]。而X2检验在评价方面应用广泛，但较依赖于选择数据段数目和位置，应用@RISK软件基于等概率数据段，即对表1中的连续型概率分布拟合时尝试使每个数据段包含相等的概率量，由此获得较高的评价依据。

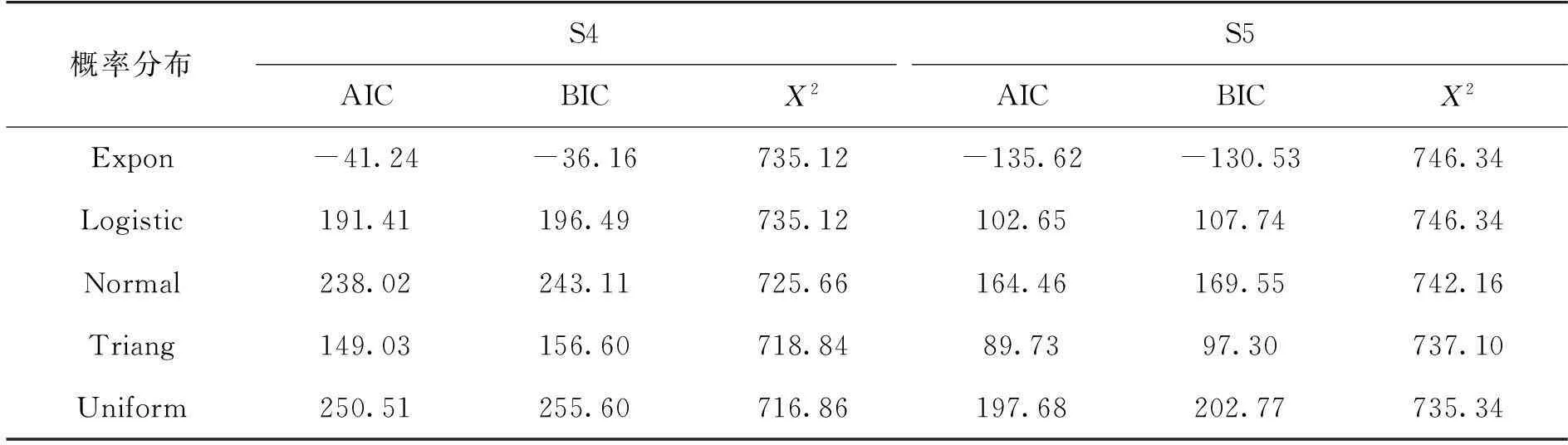
表2　不同阴性样品连续概率分布的评价(S4和S5)

表2结果表明：通过X2检验的值差别不大，以均匀分布(Uniform)为最优。但根据经验可知，微生物在食品中的污染水平符合均匀分布的可能性较小，不予考虑。而AIC和BIC优选的阴性样品概率分布都为指数分布(Expon)，对应的S4和S5场景的气单胞菌概率密度图分别如图2和图3所示，其中拟合求出的指数分布中衰减参数(β)分别为0.29和0.18，根据定义[8]，S4和S5场景的气单胞菌菌数的期望值E[Nt]分别为1/0.29和1/0.18，即3.45 lg(CFU/g)和5.56 lg(CFU/g)。

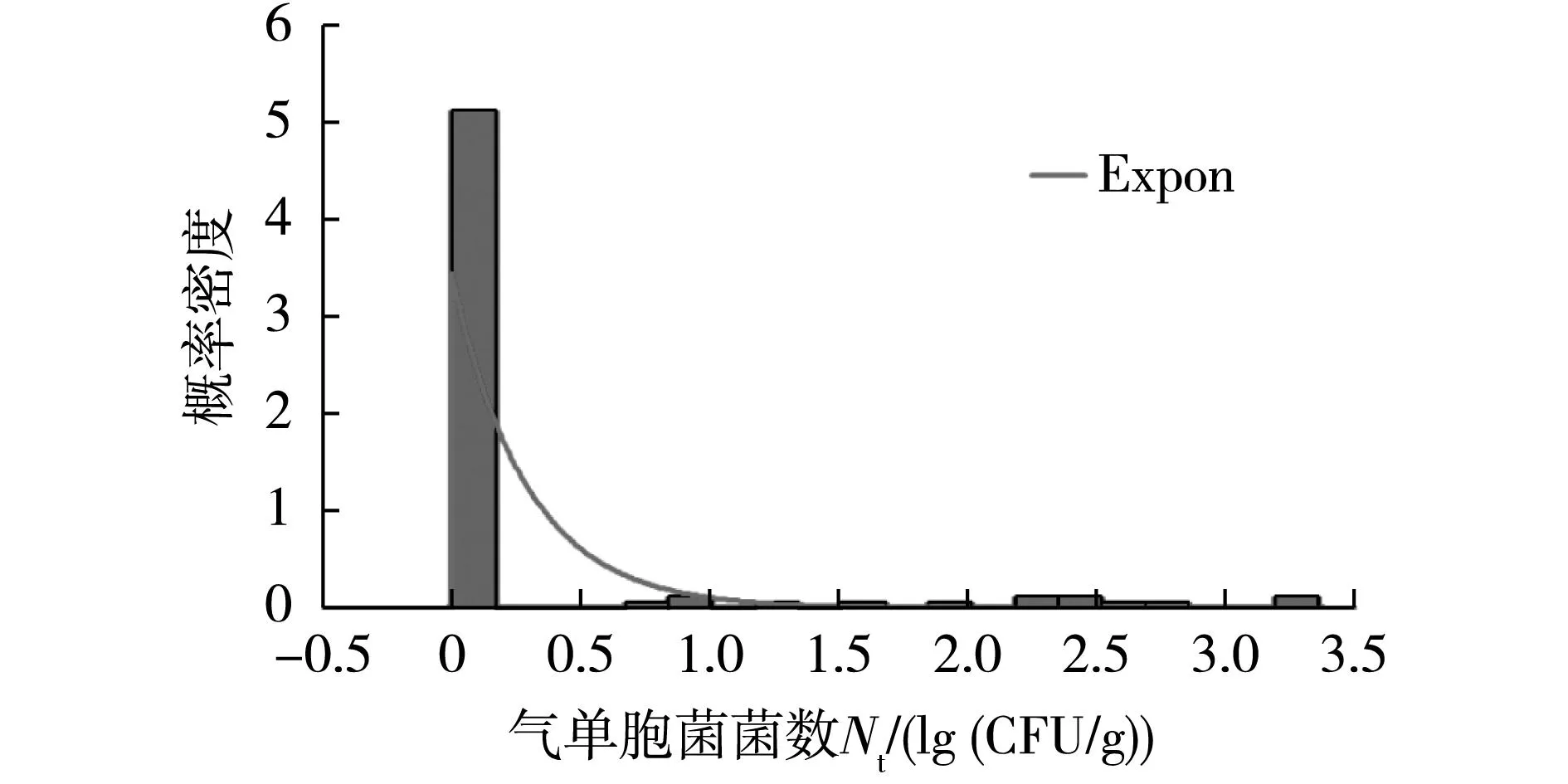
图2　　　应用Expon函数拟合S4场景的气单胞菌概率密度Fig.2　　　Aeromonas spp.probability density of Scenario 4　　　fitted by Exponential function

假设S4和S5选择指数分布(Expon)作为气单胞菌的初始污染水平，与上述的S2和S3类似，通过软件模拟分析，求得最终的气单胞菌菌数超过5 lg(CFU/g)的概率分别为32.4%和59.0%，这分别与S2和S3的结果(33.6%和69.3%)差异不显著(P>0.05)，但与S1的结果(22.1%)差异显著(P<0.01)。由此可知，致病菌初始污染水平的概率分布选择离散型(S2和S3)或者连续型(S4和S5)，不是影响定量暴露评估结果的显著因素。

另外，通过安德森-达林(A-D)检验按照表1列出的概率分布，对S4和S5进行评价，结果都分别为正态分布(Normal)最优；通过K-S检验为逻辑分布(Logistic)最优(数据未列出)。A-D检验和 K-S检验最初都是为拟合验证而开发的检验，有观点认为适合于数据点较多的情况，不可直接作为确定替代分布的工具[9]。因此优选概率分布的标准仍以AIC和BIC为准。

2.3离散分布与连续分布的选择

离散分布和连续分布是概率统计常用的两类变量分析。简单地说，符合离散分布的变量可以一一列举，而符合连续分布的不能一一列举，但变量充满某一空间。从已有的QMRA研究来看，大多数设定致病菌符合离散分布，比如世界卫生组织(WHO)、联合国粮食及农业组织(FAO)完成的不同食品中沙门菌、单增李斯特菌、阪崎肠杆菌、弧菌、病毒等的定量风险评估研究[10]，主要依据是对致病菌污染水平采用定量检测方法，如CFU/mL或CFU/g，并假设检测结果是独立和离散的，采用离散分布更能代表实际污染情况。但当前有些致病菌的检测方法采用最大可能数(MPN/g或MPN/mL)，本身即为概率方法，基于这类方法开展QMRA分析需特别谨慎[11]，推荐选用连续分布。

另外，CFU和MPN是并非可以互相换算的微生物计数方法，有专门研究二者之间的统计关系[12]，但并非通用于所有的病源性微生物；同时，与CFU方法原理不同，MPN方法不存在阴性样品的问题，其原理可参考Cochan的经典论述[13]。本研究的数据基于CFU的菌落计数方法，故选用离散分布对阴性样品中致病菌的数量进行描述(S1、S2和S3)，同时还利用连续分布对致病菌的数量进行描述(S4、S5)，并探讨了设定不同分布的结果差异，结果表明离散分布和连续分布计算得到的食物中毒发病率差异不显著(S2和S4之间、S3和S5之间)。可能原因是样本数较大(文献[2]中的100个)，但是如果样本数过小，比如低于30个，仍建议选用离散分布，更符合实际检测结果。

2.4评价概率分布的参数选择

不同连续概率分布表达式代表的意义差别较大(表1)，如何选择适合QMRA研究的概率分布对结果影响较大。优选可通过专家意见(Expert opinion)、历史经验(Previous experience)或统计分析(Statistical analysis)而实现[14]，本研究主要基于统计分析的几种评价参数(AIC、BIC和X2而选定指数分布(Expon)模拟致病菌的初始污染水平(图2和图3)。

对概率分布的优选，常用的评价方法包括赤池信息量准则(AIC)、贝叶斯信息准则(BIC)、卡方检验(X2)、安德森-达林检验(A-D)、科尔莫戈罗夫-斯米尔诺夫检验(K-S)和均方根误差检验(RMSE)等[15]。其中AIC和BIC统计量是利用简单表达式，使用对数似然函数计算得出的，一般认为AIC假设“真”模型不在候选集中，应用均方误差最小原则，渐进于最优模型，这种假设更符合实际情况[16]，因此首选AIC作为判断依据。另外，卡方检验也可用于连续型或离散型样本数据的拟合优度检验，一般通过任意选择数据段进行观测值和期望值的比较，可通过等概率数据段的方式来消除数据段选择的任意性(如@RISK软件)。作为类似的模型“信息标准”检验参数，AIC和BIC结果类似，AIC基于渐进最优的假设，而BIC不是，按照Yang[16]的分析，AIC趋向于对强度弱于BIC的参数数量进行惩罚，AIC更易于使概率分布获得收敛。而其他几种检验参数(X2、A-D和K-S)都为常用评价方法，各有优缺点，可作为评价概率分布参数选择的辅助参考。

同时，专家意见和历史经验在选择概率分布也是非常重要的参考依据，比如QMRA研究中常涉及的冰箱温度、贮藏时间等，多为符合正态分布(Normal)，这些参数可以直接选用合适的概率分布来描述。

2.5阴性样品的概率分布对风险评估结果的影响

当前食品风险评估发展迅速，许多学者也质疑此类研究数据缺乏和假设过多[17]。解决此类难题的方法有很多，如前述提高微生物检测精度，如果能得出微生物的真实污染水平，对风险评估模型的输出值可靠性会大大提高。但是，风险评估本身就是一个概率问题[5]，很难真正完全按照定值评价的模式来实现，而概率模式对食品安全控制和风险管理更有实际意义(比如本文场景S1的最终污染水平导致食物中毒的概率为22.1%)，已证实比单纯依靠点估计模式更优[18]。需要注意的是，用概率方法进行风险评估，为提高风险特征描述的严谨性，模型本身的不确定性和变异性需要区别对待[19]。

本研究结果表明不同阴性样品污染水平的假设对定量暴露评估结果的影响显著，设定为零值的S2和设定为检测限值的S3，预测得到的食物中毒概率分别为33.6%和69.3%，如果直接用来作为风险管理和控制的理论参考，势必严重失实并造成公众恐慌。因此考虑阴性样品(低于检测限)的致病菌分布情况或者改进现在常用的Jarvis经典公式[2-4]，提高风险评估的科学性和严谨性非常必要。

3结论

阴性样品分布对微生物定量风险评估结果影响显著，以冷却猪肉中气单胞菌研究为例，设定阴性样品全为零值或全为最高值(检测限)，由此预测得到的食物中毒概率显著高于常规的Jarvis公式方法。再以常用的连续型概率分布拟合上述2种极端的场景，通过AIC、BIC等评价参数进行比较，表明指数分布(Expon)作为气单胞菌的初始污染水平最优。今后微生物定量风险评估研究不应忽略阴性样品分布的设定，以此提高风险评估结果的可靠性。

参考文献：

[1]CAC.Working principles for risk analysis for food safety for application by governments[EB/OL].[2015-03-18].http://www.codexalimentarius.net/web/more_info.jsp?id_sta=10751.

[2]董庆利,高翠,郑丽敏,等.冷却猪肉中气单胞菌的定量暴露评估[J].食品科学,2012,33(15):24-27.

[3]董庆利,郑丽敏.即食凉拌菜中单增李斯特菌的定量暴露评估[J].生物加工过程,2013,11(5):55-60.

[4]董庆利.蒸煮米饭中蜡样芽胞杆菌的定量暴露评估[J].食品科学,2013,34(21):306-310.

[5]DONG Q,BARKER G C,GORRIS L G M,et al.Status and future of quantitative microbial risk assessment in China[J].Trends Food Sci Technol,2015,42(1):70-80.

[6]美国Palisade公司.@RISK Microsoft© Excel 风险分析和模拟插件用户指南[M].6版.New York:Palisade Corporation,2013.

[7]FELLER W.An introduction to probability theory and its applications[M].3rded.New York:John Wiley & Sons,Inc.1968.

[8]KNUTH D E.The art of computer programming,Volume 2:semi-numerical algorithms[M].3rded.Boston:Addison-Wesley,2009：133-134.

[9]HASTIE T,TIBSHIRANI R,FRIEDMAN J.The elements of statistical learning:data mining,inference,and prediction[M].New York:Springer-Verlag:120-127.

[10]WHO/FAO.Risk Analysis[EB/OL].[2015-03-18].http://www.who.int/foodsafety/micro/riskanalysis/en/

[11]POUILLOT R,HOELZER K,CHEN Y,et al.Estimating probability distributions of bacterial concentrations in food based on data generated using the most probable number (MPN) method for use in risk assessment[J].Food Control,2013,29(2):350-357.

[12]SARTORY D P,GU H,CHEN C H.Comparison of a novel MPN method against the yeast extract agar (YEA) pour plate method for the enumeration of heterotrophic bacteria from drinking water[J].Water Res,2008,42(13):3489-3497.

[13]COCHRAN W G.Estimation of bacterial densities by means of the ″Most Probable Number″[J].Biometrics,1950,6(2):105-116.

[14]USDA/FSIS/EPA.Microbial risk assessment guideline:pathogenic organisms with focus on food and water[M].[s.l.]:FSIS Publication,2012.

[15]VOSE D.Risk analysis:a quantitative guide[M].3rded.London:John Wiley & Sons,Ltd.,2008.

[16]YANG Y.Can the strengths of AIC and BIC be shared： a conflict between model identification and regression estimation[J].Biometrika,2005,92(4):937-950.

[17]ROMERO-BARRIOS P,HEMPEN M,MESSENS W,et al.Quantitative microbiological risk assessment (QMRA) of food-borne zoonoses at the European level[J].Food Control,2013,29(2):343-349.

[18]董庆利,王忻,王海梅,等.冷却猪肉中气单胞菌暴露评估的不确定性和变异性[J].食品科学,2014,35(15):101-104.

[19]POUILLOT R,CHEN Y,HOELZER K.Modeling number of bacteria per food unit in comparison to bacterial concentration in quantitative risk assessment:impact on risk estimates[J].Food Microbiol,2015,45(2):245-253.

(责任编辑管珺)

Effect and optimization ofAeromonasspp.probability distribution in negative samples of chilled pork

DONG Qingli1,SONG Xiaoyu2,DING Tian3,LIU Qing1

(1.School of Medical Instrument and Food Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China;2.China National Center for Food Safety Risk Assessment,Beijing 100021,China;3.College of Biosystems Engineering and Food Science,Zhejiang University,Hangzhou 310058,China)

Abstract：This study was designed to verify the effects of pathogen in the negative samples on quantitative microbiological risk assessment (QMRA). Previous research on QMRA of Aeromonas spp. in chilled pork was taken as an example,and two scenarios of Aeromonas spp. in the negative samples,zero and maximum value (detection limit),respectively,were simulated in quantitative exposure assessment. The predictive food-poison probability of the two scenarios was 33.6% and 69.3%,respectively,and these values were higher than the previous results of 22.1% based on Jarvis function to estimate the possible pathogen distribution in negative samples significantly (P<0.01). Moreover,Akaike Information Criterion (AIC),Bayesian Information Criterion (BIC)， X2， and other parameters were applied for evaluating pathogen in negative sample with different continuous probability distributions. Exponential distribution proved to be better than Logistic,Normal,Triangle and Uniform with AIC values equaling to -41.24 and -135.62 under the two simulated scenarios,respectively,lower than the results of other distributions. In conclusion,pathogen distribution in negative sample should be noted and further optimized during QMRA in future.

Keywords：negative sample; Aeromonas spp.; probability distribution; risk assessment

中图分类号：TS 201.3；TS 251.44

文献标志码：A

文章编号：1672-3678(2016)02-0064-06

作者简介：董庆利(1979—)，男，山东临沂人，博士，副教授，研究方向：畜产品质量与安全控制，E-mail:dongqingli@126.com

基金项目：国家自然科学基金(31271896、31371776)；上海市科委重点支撑项目(13430502400)；上海市科委长三角科技联合攻关领域项目(15395810900)

收稿日期：2015-03-18

doi:10.3969/j.issn.1672-3678.2016.02.012