适于Russell流体因子提取的孔隙弹性介质反射系数近似方程

张世鑫,杜向东,韩文明,孙林洁

(中海油研究总院,北京100027)



适于Russell流体因子提取的孔隙弹性介质反射系数近似方程

张世鑫,杜向东,韩文明,孙林洁

(中海油研究总院,北京100027)

摘要:Russell流体因子是表征储层孔隙流体特征的重要敏感流体因子,其提取结果的可靠性是决定流体判识质量的核心问题之一。叠前地震反演是提取流体因子的主要途径,而反射系数近似方程是叠前反演的基础。结合Biot-Gassmann多孔弹性介质理论对反射系数近似方程进行了重新推导,得到了包含Russell流体因子的孔隙弹性介质反射系数线性近似方程;通过分析方程的精度和反演敏感特征,验证了新反射系数近似方程的可靠性和Russell流体因子项的高反演敏感度;最终基于贝叶斯反演框架的AVO反演实现了Russell流体因子的定量提取。模型试算和实际应用结果表明,基于新反射系数近似方程的叠前反演方法能够稳定可靠地从地震资料中提取Russell流体因子,为储层流体识别提供了一种新的流体因子计算方法。

关键词:Russell流体因子;反射系数近似方程;叠前地震反演;流体识别

地震波所蕴含的丰富的动力学与运动学信息有助于揭示地下岩层及其孔隙流体特征。随着物探技术的进步,以地震资料为主体的地下岩层孔隙流体识别技术已成为现阶段储层精细描述的关键技术之一。在保证地震资料品质的前提下,储层流体识别精度主要取决于所选取的流体因子是否敏感及其计算方式是否可靠[1-5]。

现今,单纯依靠振幅异常的“亮点”等定性检测技术已无法满足复杂岩性油气藏的流体识别需求,SMITH等[6]率先提出了利用纵、横波速度相对变化率的加权叠加检测烃类异常的方法,并首次提出了流体因子的概念;随后,GIDLOW等[7]和FATTI等[8]利用纵、横波阻抗相对变化率构建了新流体因子;GRAY等[9]则使用拉梅参数的相对变化率为流体因子进行流体判识。流体识别的研究重点也逐渐从定性检测过渡到利用流体因子实现储层含流体异常的定量判识,并且随着地震反演技术的发展,流体因子类型也逐步从反射系数域发展到阻抗域。GOODWAY等[10]提出了拉梅常数-密度(Lambda-Mu-Rho,简称LMR)技术,利用储层的拉伸剪切特性区分储层含流体类型;QUAKENBUSH等[11]提出了泊松阻抗的概念;RUSSELL等[12-13]基于多孔弹性介质岩石物理理论,提出了可以反映孔隙流体弹性效应的Russell流体因子和Gassmann流体/孔隙项,通过研究干岩石纵横波速度比的取值,认为LMR技术只是Russell流体因子的特例,并且与其它利用权差运算得到的流体因子相比,Russell流体因子和Gassmann流体/孔隙项具有更明确的物理意义和更敏感的流体判识能力。目前,二者在碎屑岩储层流体判识中占据重要位置,且研究发现,虽然两者对碎屑岩储层流体判识的敏感度基本一致,但是Russell流体因子综合了Gassmann流体/孔隙项和密度项参数,对一些固结成熟的碎屑岩储层,表现为更高的流体判识敏感性[1,14]。

叠前地震反演作为提取储层弹性参数的主要途径,其反演结果的可靠性直接影响流体因子的可靠性。在叠前反演中,反射系数近似方程是反演框架构建的基础,如包含纵、横波速度和密度的Aki-Richards近似等[15]。由于反射系数近似方程中的弹性参数信息权重存在较大差异,即反射系数近似方程中的弹性参数具有不同的反演敏感性,且受地震反演本身的“病态解”影响,叠前反演得到的弹性参数不可避免地存在多解性[16],而通过间接代数运算得到的流体因子则会进一步放大累计误差,影响流体识别的可靠性[17]。为了提高流体因子的估算精度,学者们进行了一系列研究,RUSSELL等[13]基于多孔弹性介质岩石物理理论首次建立了包含Gassmann流体/孔隙项、剪切模量和密度项的反射系数近似方程,提出了从叠前道集资料中直接估算Gassmann流体/孔隙项,并以此作为流体因子直接进行储层流体识别的研究思路。随后,敏感流体因子的直接反演逐步成为学者们研究的热点,印兴耀等[18]利用弹性阻抗反演实现了Gassmann流体/孔隙项的估算;杨培杰等[19]基于Russell反射系数近似公式提出了可变点约束AVO叠前反演算法,提高了Gassmann流体/孔隙项的估算精度。考虑到流体因子的敏感性具有区域适用性,围绕Russell流体因子的直接反演,学者们也进行了一些研究,印兴耀等[1]基于包含Russell流体因子的两项弹性阻抗方程实现了Russell流体因子的直接提取,取得了较好的深层流体识别应用效果,同时也指出在大角度叠前地震资料可用的情况下,要尽可能借助大角度地震资料来进一步提高Russell流体因子计算的可靠性。本文为充分利用叠前地震资料包含的有效信息,在多孔弹性介质岩石物理理论指导下,推导了包含Russell流体因子的3项反射系数近似方程,在贝叶斯反演理论框架下利用叠前AVO反演实现了Russell流体因子的直接反演,为流体因子的可靠计算提供了一种新的方法。

1新反射系数近似方程

在地震波引起孔隙流体压力变化符合Biot-Gassmann多孔弹性介质理论应用条件的前提下[20-21],RUSSELL等[12]利用孔隙弹性介质的力学特征对含流体多孔介质的纵波速度与横波速度进行了改写,并进一步推导得到了Russell流体因子F,即:

(1)

式中:f为Gassmann流体/孔隙项;ρ为多孔流体饱和弹性介质的密度;vP为纵波速度;vS为横波速度;γdry为干岩石纵横波速度比。

为得到包含Russell流体因子的反射系数近似方程,对Aki-Richards反射系数近似方程进行重新改写。Aki-Richards反射系数近似方程为:

(2)

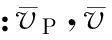
对(2)式两边同时乘以(vPρ)2,得到:

(3)

对(1)式两边微分,则有:

(4)

整理后可以得到:

(5)

将(5)式代入(3)式得:

(6)

又因为流体因子可以表示为:

(7)

两边微分并变形可以得到:

(8)

将(8)式代入(6)式,并进行变换可以得到:

(9)

又因为:

(10)

(11)

(9)式最终化为:

(12)

(12)式为包含Russell流体因子F,剪切模量μ和密度ρ的孔隙弹性介质反射系数近似方程。与常规反射系数近似方程不同的是该方程考虑了孔隙流体的弹性效应,不仅更直观地表征了地震波中蕴含的流体信息,而且有利于流体因子的定量反演。

2近似精度与反演敏感性分析

2.1近似精度分析

利用RUSSELL等[13]提出的砂岩模型来验证公式(12)的精度。砂岩模型为两种双层砂岩模型,模型参数如表1所示,模型一为上层砂岩含气(含气饱和度为90%,含水饱和度为10%),下层砂岩含水,两层孔隙度均为25%;模型二的两层砂岩均含水,但孔隙度存在差异,上层孔隙度为25%,下层孔隙度为15%。分别采用精确Zoeppritz方程、Aki-Richard近似方程和本文新推导的反射系数近似方程计算这两种模型中砂岩界面的反射系数,并比较了两种近似方程与精确Zoeppritz方程之间的相对误差,其结果如图1和图2所示。

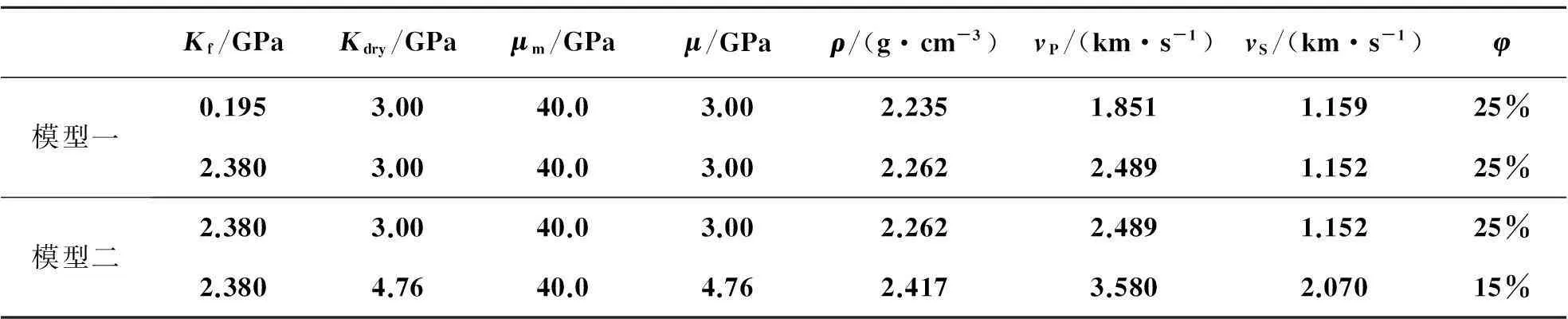
表1　两种砂岩模型参数[13]

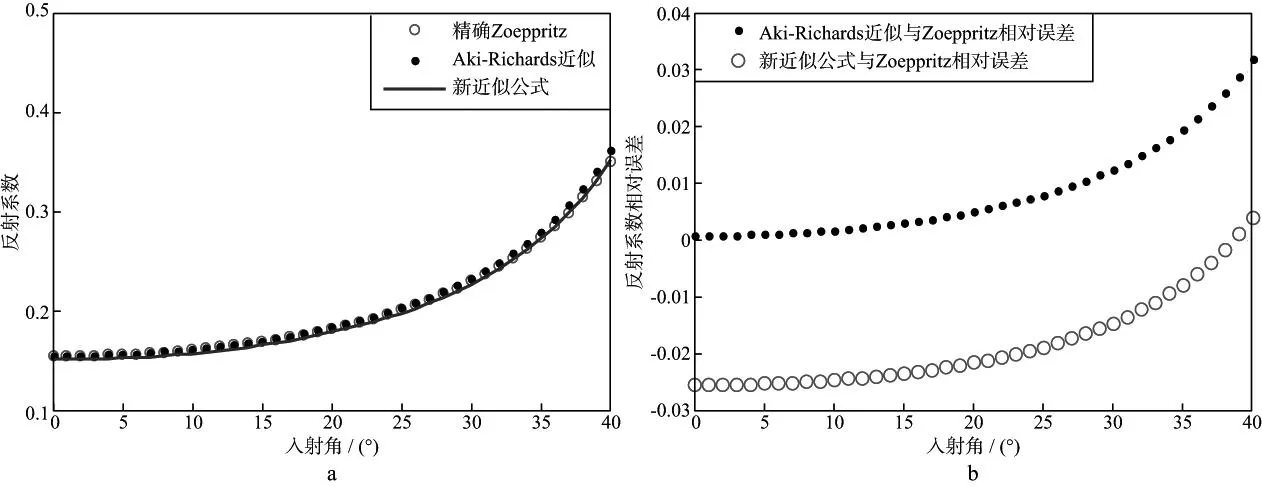
图1　模型一的反射系数计算结果a 反射系数; b 反射系数相对误差

从图1a可以看到,当界面两侧介质孔隙度没有变化时,(12)式与Zoeppritz精确方程的结果匹配较好;从图1b可以看到,当入射角为0时,公式(12)与Zoeppritz方程的相对误差为-2.5%,且随着入射角的增加,两者之间的相对误差逐渐减小。从图2a则可以看到,当界面两侧砂岩孔隙度不同时,公式(12)在小角度入射时,与精确解相差不大,随着入射角的增大,公式(12)的计算数值逐渐偏离精确Zoeppritz结果;由图2b可知,公式(12)与Zoeppritz精确方程的最大误差在入射角为40°时出现,相对误差为-8%,但是公式(12)的计算值与Aki-Richards近似的结果基本一致,这是因为新反射系数近似方程本身是从Aki-Richards近似推导出来的,两者精度基本一致,误差仅在于干岩样纵横波速度比值的选取;考虑到反射系数近似是建立在界面两侧弹性差异较小的前提下,而孔隙度的变化对岩石模量的影响要大于孔隙流体变化造成的影响,因此界面两侧孔隙度的变化会产生更大的大角度近似误差,但从总体上说,公式(12)在小角度入射情况下仍然可以满足反射系数的近似精度。考虑到实际应用中的角度道集一般不超过35°,即在误差允许的范围内使用新的反射系数近似方程进行叠前反演是可行的。

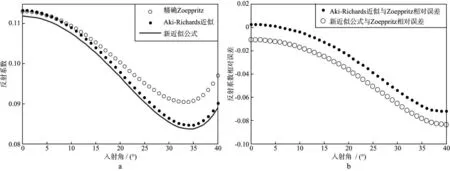
图2　模型二的反射系数计算结果a 反射系数; b 反射系数相对误差

2.2反演敏感性分析

由URSIN等[22],NICOLAO等[23]的研究得出,不同反射系数线性近似方程所表达的弹性参数信息是不同的,进而影响了相应弹性参数反演的可靠性。为检验基于公式(12)的Russell流体因子的反演可行性,在此采用NICOLAO等[23]提出的信息敏感分析方法对公式(12)包含的弹性参数信息进行定量分析。

将公式(12)以矩阵形式表示为:

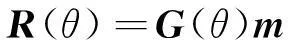
(13)

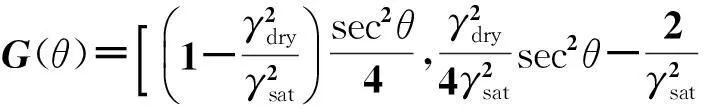
NICOLAO等[23]指出,通过分析模型空间特征值及特征向量,可以定量分析反射系数近似方程中蕴含的弹性参数的信息敏感性。其中,正演映射矩阵的大特征值及对应的特征向量表示信息敏感的弹性参数,而小特征值则表示信息不敏感、在反演中不易得到的弹性参数。

对正演映射矩阵G(θ)进行奇异值分解:

(14)

式中:U表示数据空间的特征向量;Λ表示奇异值对角矩阵;V表示模型空间的特征向量。设γsat=2.000,γdry=1.732,最大入射角范围为0～50°。图3 给出了特征值随最大入射角的变化曲线。其中,特征值的大小用分贝(20lgλ)表示。由图3可知,所有特征值都随最大入射角的增加而增大,这说明模型空间包含的弹性参数信息量随着入射角的增加而增大,即入射角越大,反演的弹性参数越可靠。在最大入射角为30°时,第一特征值几乎是第二特征值所包含能量的100倍,是第三特征值所包含能量的10000倍。考虑到第三特征值包含能量很少,且随入射角的增加也很难确定待反演的参数组合,因此只分析第一、第二特征值对应的特征向量即可确定易于反演的弹性参数。

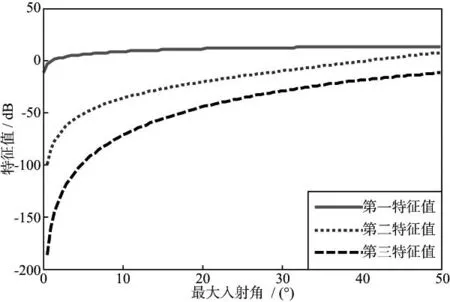
图3　模型空间中的3个特征值随最大入射角的变化曲线

图4a和图4b分别给出了模型空间第一特征值和第二特征值对应的特征向量的方向余弦随最大入射角的变化曲线。当方向余弦为0时,无法反演该弹性参数,且数值偏离0的程度越大,反演该弹性参数的难度越小。从图4a可知,当最大入射角较小时,第一特征值对应的Δμ/μ特征向量方向余弦偏离0的幅度最大,其次是ΔF/F,Δρ/ρ偏离0的幅度最小;随着最大入射角的增加,ΔF/F和Δρ/ρ的特征向量方向余弦偏离0的幅度逐渐增大,而Δμ/μ则逐渐减小;当最大入射角大于27°时,ΔF/F的偏离幅度要高于Δμ/μ,即Russell流体因子信息随角度的增加而增大,而Δρ/ρ的幅度则始终很小。图4b中3个弹性参数的特征向量方向余弦偏离0的幅度相差不大,相比较而言,Δρ/ρ的偏离幅度最大,其次是ΔF/F和Δμ/μ。

由于第一特征值对应的信息量最大,第二特征值对应的信息只有在入射角很大的情况下才能生效。由图4可知,基于公式(12)可较好地确定ΔF/F和Δμ/μ,而确定Δρ/ρ的难度相对较大,且为了保证ΔF/F的准确性,需选用入射角大于30°的地震道集。因此,当最大入射角大于30°时,ΔF/F具有最高的反演敏感性,这与印兴耀等[1]的认识也是一致的。

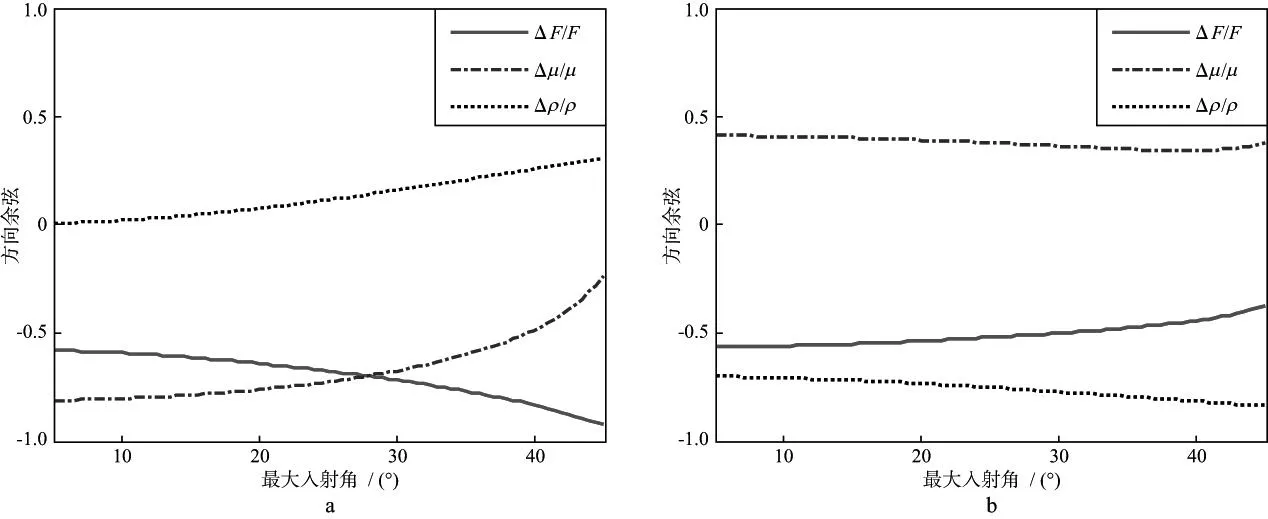
图4　模型空间中特征向量的方向余弦随最大入射角的变化曲线a 第一特征值对应的方向余弦; b 第二特征值对应的方向余弦

3Russell流体因子反演

3.1反演方程

贝叶斯反演理论能够利用必要的先验约束缩小解空间,且保证反演结果的稳定性[24-26]。在贝叶斯反演框架下建立了基于新反射系数近似方程的反演方程,通过先验地质约束最大似然的反演过程,实现了Russell流体因子的直接反演。

一般情况下,地震记录中的噪声信息服从正态分布,即似然函数是高斯分布。为了保护地下的弱反演信息,在此假设反映地下弹性参数相对变化量特征的先验信息服从柯西分布,利用贝叶斯公式将似然函数与先验函数结合起来,得到包含反演参数m的后验概率函数P(m|d):

(15)

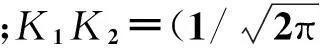
通过求解后验概率最大化可以得到反演目标函数:

(16)

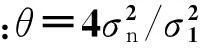
(17)

在给定初值的前提下,利用共轭梯度方法循环迭代求解公式(16)即可得到反问题的解。得到的结果是3个参数的相对变化率mF,mμ和mρ,再通过求解方程(18)可以最终得到Russell流体因子

F,剪切模量μ和密度ρ的数据体。

(18)

式中:t是时间采样点;t0是起始时间。

3.2模型测试及分析

为验证反演方法的可靠性,以实际测井资料为模型数据进行测试。模型如图5所示,用精确Zoeppritz方程得到不同采样点的P波反射系数,将其与40Hz零相位Ricker子波褶积生成叠前角度道集(角度范围为0～45°,采样间隔2ms),以此为基础对不同信噪比条件下的反演结果进行分析。图6a和图6b分别为未含噪声和信噪比为2∶1的角度道集数据。针对这两套数据,分别采用直接反演方法和常规方法(先反演得到纵、横波速度和密度,再通过间接代数运算得到流体因子等参数)反演得到Russell流体因子、剪切模量和密度,与模型数据进行对比,结果如图7和图8所示。图7和图8中黑色实线代表实际模型的反演结果,红色虚线代表利用本文方法直接反演的结果,蓝色虚线代表利用常规方法间接计算的结果。通过比较发现,无噪声时,两种方法得到的Russell流体因子及剪切模量均与模型数据吻合较好,只有密度项的反演结果误差相对较大,这与2.2节中的反演敏感性分析结论一致;当信噪比为2∶1时,两种方法的估算精度均受到一定的影响,但与常规方法相比,本文方法直接反演的Russell流体因子以及剪切模量的总体趋势更接近实际模型,但是两种方法得到的密度项则均存在较大的差异,这是因为反射系数近似方程本身缺少密度信息,反演得到的密度参数稳定性不高,且易受噪声影响产生较大的反演误差。

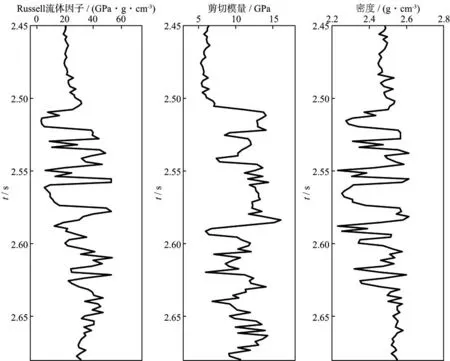
图5　地层模型曲线

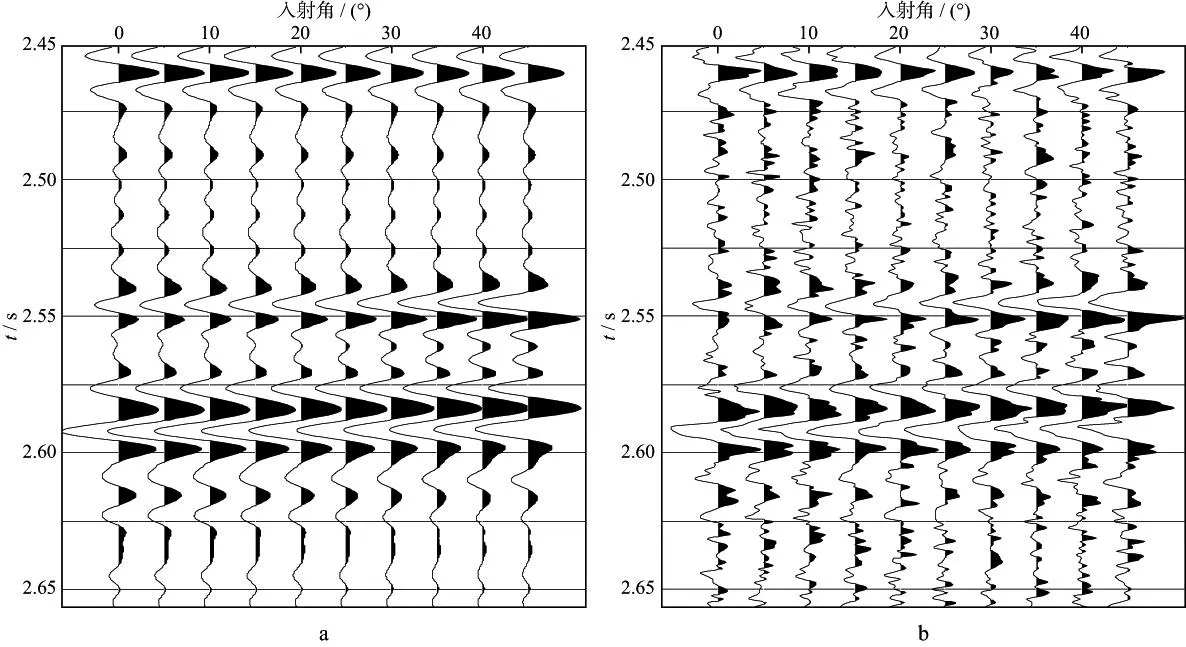
图6　模型角度道集a 无噪声角度道集; b 信噪比为2∶1的角度道集

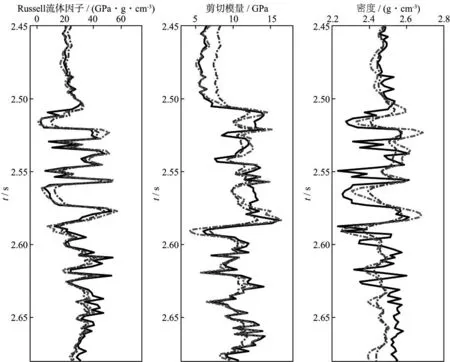
图7　无噪声反演结果

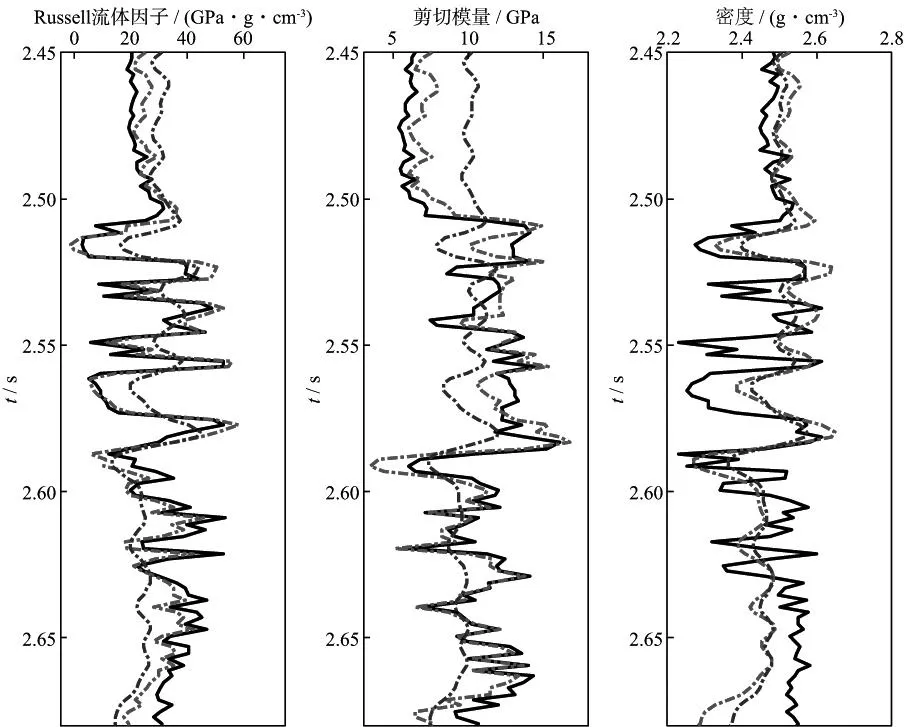
图8　信噪比为2∶1情况下的反演结果

考虑到Russell流体因子是参与储层流体识别的主体数据,为进一步比较本文方法与常规方法提取Russell流体因子的精度,对比了两种方法估算的Russell流体因子与模型数据的相对误差,结果如图9所示。图9中红色虚线代表直接反演结果的相对误差;蓝色虚线代表常规方法计算结果的相对误差。从图9可见,在无噪声情况下,两种方法估算的Russell流体因子的相对误差基本一致,但是,当有噪声时,常规间接计算方法的相对误差更大,这是因为有噪声的情况下,密度项的反演结果会存在较大的不确定性(图8),利用这种密度项进行Russell流体因子的间接计算会进一步造成误差累计,使得间接计算的Russell流体因子存在较大误差,而直接反演方法则有效规避了这种现象。考虑到实际地震数据均会存在一定的噪声,所以本文方法直接反演的Russell流体因子具有更高的可靠性。

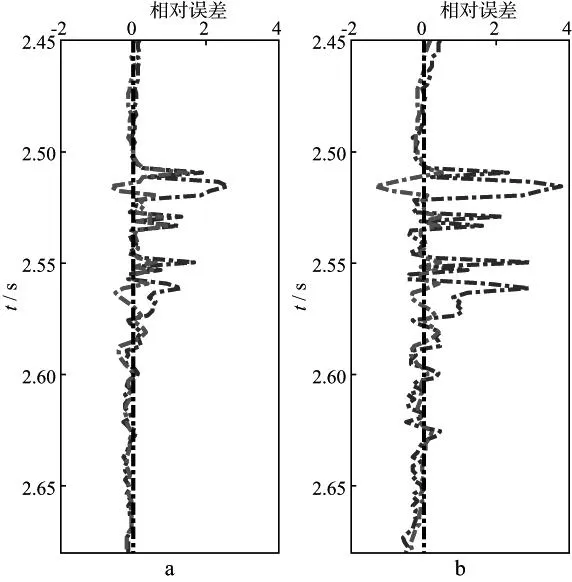
图9　无噪声(a)和信噪比为2∶1(b)情况下反演的Russell流体因子与实际模型数据的相对误差

3.3实际数据应用

实际资料来自加拿大Alberta地区的叠前道集数据,选取了100个CMP道集,每个道集含有8道,偏移距为70～560m。图10为选用的道集数据剖面,在剖面0.64～0.66s用黑色椭圆标出了含气储层位置。假设该数据不含噪声,加入白噪声使得数据信噪比为5∶1,利用本文方法直接反演得到Russell流体因子数据,结果如图11a所示;利用常规AVO三参数反演方法反演得到纵、横波速度与密度参数,再根据公式(1)计算得到的Russell流体因子如图11b所示。从图11中可以看到,虽然两者在含气目的储层位置均表现为较为明显的低值异常,但是相比较直接反演结果,间接计算结果的信噪比明显偏低,且产生了较大累计计算误差。

图10　测试道集数据(黑色椭圆表示含气储层位置)

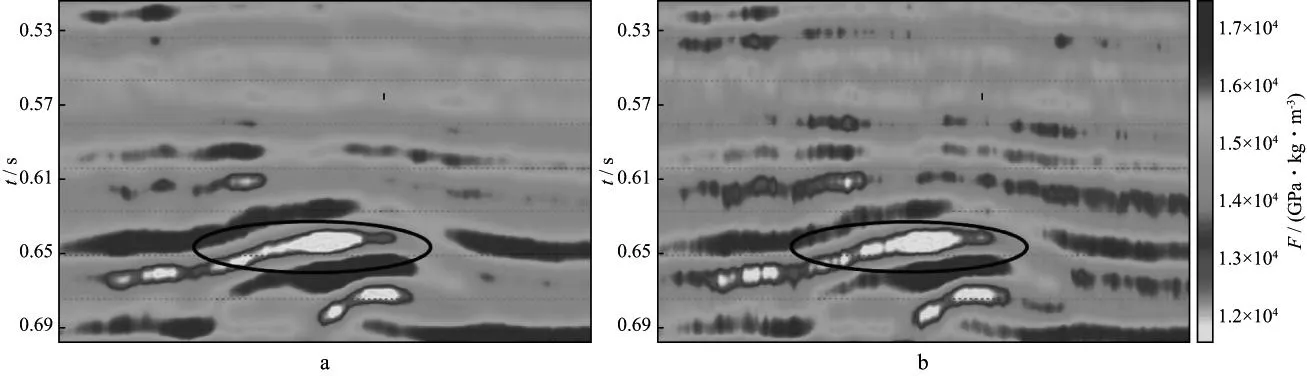
图11　测试数据的Russell流体因子计算结果a 直接定量反演结果; b 常规方法间接计算结果

为了更加清晰地对比反演结果的可靠性,图12 给出了叠前反演得到的Russell流体因子曲线和实际测井曲线(为减小尺度差异,此处将测井数据进行了Backus平均处理)。由图12可见,直接反演的Russell流体因子与实际测井曲线吻合度更高,具有更高的抗噪性,而常规方法得到的Russell流体因子则存在较大误差,这与模型测试的结果也是吻合的,即不可靠的密度项参数造成了Russell流体因子的累计误差。通过实际数据的应用也进一步验证了基于新反射系数近似方程直接反演得到的Russell流体因子更为精确。

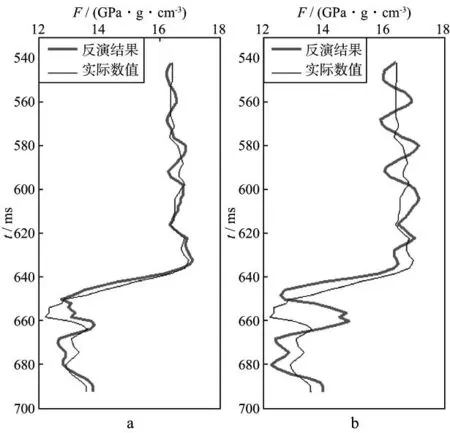
图12　叠前反演得到的Russell流体因子与实际测井曲线的对比a 基于新反射系数近似方程的反演结果与测井曲线的对比; b 常规叠前反演结果与测井曲线的对比

4结束语

包含Russell流体因子的反射系数近似方程更直观地表征了孔隙介质中的流体弹性效应。通过叠前地震反演直接提取Russell流体因子,不仅实现了叠前反演与储层流体识别的有效结合,而且为流体检测提供了更加可靠的数据基础。主要结论如下:

1) 结合Biot-Gassmann孔隙弹性介质理论推导的包含Russell流体因子的反射系数近似方程不仅可以满足精度要求,而且Russell流体因子在公式中的信息量可以保证参数反演的稳定性;

2) 基于贝叶斯理论框架的反演方法实现了Russell流体因子参数的可靠反演,有效避免了常规方法的累计误差,提高了Russell流体因子的估算精度,有助于储层流体类型的可靠判识;

3) 在实际资料的应用中,需要借助各向异性动校正等技术对叠前道集进行处理,在保证远道大偏移距数据可用的前提下,尽可能利用大角度叠前数据提高Russell流体因子反演的可靠性。

参考文献

[1]印兴耀,张世鑫,张峰.针对深层流体识别的两项弹性阻抗反演与Russell流体因子直接估算方法研究[J].地球物理学报,2013,56(7):2378-2390

YIN X Y,ZHANG S X,ZHANG F.Two term elastic impedance inversion and Russell fluid factor direct estimation method for deep reservoir fluid identification[J].Chinese Journal of Geophysics,2013,56(7):2378-2390

[2]郑静静,印兴耀,张广智.流体因子关系分析以及新流体因子的构建[J].地球物理学进展,2011,26(2):579-587

ZHENG J J,YIN X Y,ZHANG G Z.Fluid factor analysis and the construction of the new fluid factor[J].Progress in Geophysics,2011,26(2):579-587

[3]管路平.地震叠前反演与直接烃类指示的探讨[J].石油物探,2008,47(3):228-234

GUAN L P.Pre-stack inversion and direct hydrocarbon indicator[J].Geophysical Prospecting for Petroleum,2008,47(3):228-234

[4]郝前勇,印兴耀,王玉梅,等.弹性模量流体因子在永新工区储层预测中的应用[J].石油物探,2012,51(5):502-507

HAO Q Y,YIN X Y,WANG Y M,et al.Application of elastic modulus fluid factor on reservoir prediction at Yongxin Block[J].Geophysical Prospecting for Petroleum,2012,51(5):502-507

[5]李超,印兴耀,张广智,等.基于贝叶斯理论的孔隙流体模量叠前AVA反演[J].石油物探,2015,54(4):467-476

LI C,YIN X Y,ZHANG G Z,et al.Prestack AVA inversion for pore fluid modulus based on the Bayesian theory[J].Geophysical Prospecting for Petroleum,2015,54(4):467-476

[6]SMITH G C,GIDLOW P M.Weighted stacking for rock property estimation and detection of gas[J].Geophysical Prospecting,1987,35(8):993-1014

[7]GIDLOW P M,SMITH G C,VAIL P J.Hydrocarbon detection using fluid factor traces,a case study:how useful is AVO analysis?[J].Technical Program and Abstracts of Joint SEG/EAEG Summer Research Workshop,1992:78-89

[8]FATTI J L,VAIL P,SMITH G C,et al.Detection of gas in sandstone reservoirs using AVO analysis:a 3-D seismic case history using the geostack technique[J].Geophysics,1994,59(9):1362-1376

[9]GRAY D,GOODWAY B,CHEN T.Bridging the gap:using AVO to detect changes in fundamental elastic constants[J].Expanded Abstracts of 69thAnnual Internat SEG Mtg,1999:852-855

[10]GOODWAY B,CHEN T,DOWNTON J.Improved AVO fluid detection and lithology discrimination using Lamé petrophysical parameters;“λρ”,“μρ”,&“λ/μfluid stack”,from P and S inversions[J].Expanded Abstracts of 67thAnnual Internat SEG Mtg,1997:183-186

[11]QUAKENBUSH M,SHANG B,TUTTLE C.Poisson impedance[J].The Leading Edge,2006,25(2):128-138

[12]RUSSELL B H,HEDLIN K,HILTERMAN F J.Fluid-property discrimination with AVO:a Biot-Gassmann perspective[J].Geophysics,2003,68(1):29-39

[13]RUSSELL B H,GRAY D,HAMPSON D P.Linearized AVO and poroelasticity[J].Geophysics,2011,76(3):C19-C29

[14]张世鑫.基于地震信息的流体识别方法研究与应用[D].青岛:中国石油大学(华东),2012

ZHANG S X.Methodology and application of fluid identification with seismic information[D].Qingdao:China University of Petroleum,2012

[15]AKI K,RICHARDS P G.Quantitative seismology[M].2nd ed.San Francisco:W H Freeman and Co,2002:153-154

[16]TARANTOLA A.Inverse problem theory and methods for model parameter estimation[M].Philadelphia:SIAM,2005:5-8

[17]王保丽,印兴耀,张繁昌.基于Gray近似的弹性波阻抗方程及反演[J].石油地球物理勘探,2007,42(4):435-439

WANG B L,YIN X Y,ZHANG F C.Gray approximation-based elastic wave impedance equation and inversion[J].Oil Geophysical Prospecting,2007,42(4):435-439

[18]印兴耀,张世鑫,张繁昌,等.利用基于Russell近似的弹性波阻抗反演进行储层描述和流体识别[J].石油地球物理勘探,2010,45(3):373-380

YIN X Y,ZHANG S X,ZHANG F C,et al.Utilizing Russell approximation based elastic wave impedance inversion to conduct reservoir description and fluid identification[J].Oil Geophysical Prospecting,2010,45(3):373-380

[19]杨培杰,王长江,毕俊凤,等.可变点约束叠前流体因子直接提取方法[J].地球物理学报,2015,58(6):2188-2200

YANG P J,WANG C J,BI J F,et al.Direct extraction of the fluid factor based on variable point-constraint[J].Chinese Journal of Geophysics,2015,58(6):2188-2200

[20]BIOT M A.Mechanics of deformation and acoustic propagation in porous median,low frequency range[J].Journal of the Acoustical Society of America,1956,28(2):168-178

[21]GASSMANN F.Über die elastizität poröser median.Vier.Der Natur[J].Gesellschaft in Zürich,1951,96:1-23

[22]URSIN B,TJALAND E.Information content of the elastic reflection matrix[J].Expanded Abstracts of 62ndAnnual Internat SEG Mtg,1992:796-799

[23]NICOLAO A D,DRUFUCA G,ROCCA F.Eigenvalues and eigenvectors of linearized elastic inversion[J].Geophysics,1993,58(5):670-679

[24]WUBSHET M A.Regularization of the AVO inversion problem by means of a multivariate Cauchy probability distribution[D].Alberta:University of Alberta,2010

[25]张世鑫,印兴耀,张繁昌.基于三变量柯西分布先验约束的叠前三参数反演方法[J].石油地球物理勘探,2011,46(5):737-743

ZHANG S X,YIN X Y,ZHANG F C.Prestack three term inversion method based on trivariate Cauchy distribution prior constraint[J].Oil Geophysical Prospecting,2011,46(5):737-743

[26]印兴耀,周琪超,宗兆云,等.基于t分布为先验约束的叠前AVO反演[J].石油物探,2014,53(1):84-92

YIN X Y,ZHOU Q C,ZONG Z Y,et al.AVO inversion witht-distribution as priori constraint[J].Geophysical Prospecting for Petroleum,2014,53(1):84-92

(编辑:陈杰)

A reflection coefficient approximation equation of poroelastic media for Russell fluid factor estimation

ZHANG Shixin,DU Xiangdong,HAN Wenming,SUN Linjie

(CNOOCResearchInstitute,Beijing100027,China)

Abstract:The Russell fluid factor is an important sensitive parameter for reservoir pore-fluid identification and the estimation techniques for Russell fluid factor plays a key role to the quality of reservoir fluid identification.The prestack seismic inversion based on the reflection coefficient approximation equation is the main approach to estimate fluid factors.With the help of Biot-Gassmann poroelastic theory,the Aki-Richards reflection coefficient approximation is rearranged to get a new linear approximation equation containing the Russell fluid factor parameter.Analytical analysis is carried out to check the accuracy and inversion sensitivity of the new approximation equation,which shows the reliability of the new reflection coefficient approximation and high inversion sensitivity of Russell fluid factor term.Finally,the directly quantitative inversion of pore-fluid impedance is realized based on the Bayesian AVO inversion.The model test and real application denote the feasibility and stability of this Russell fluid factor estimation technique.This is proposed as a new fluid estimation approach for reservoir fluid identification.

Keywords:Russell fluid factor,reflection coefficient approximation equation,prestack seismic inversion,fluid identification

文章编号:1000-1441(2016)02-0178-10

DOI:10.3969/j.issn.1000-1441.2016.02.003

中图分类号:P631

文献标识码:A

基金项目:国家科技重大专项(2011ZX05030-004)资助。

作者简介:张世鑫(1985—),男,博士,主要从事地震资料解释、储层油气预测等方面的研究工作。

收稿日期:2015-03-24;改回日期:2015-12-25。

This research is financially supported by the National Science and Technology Major Project of China (Grant No.2011ZX05030-004).