灰色直接迭代建模在武器故障预报中的应用

黄　莹

（1.武警工程大学，西安　710086；2.西安交通大学制造系统工程国家重点实验室，西安　710049）



灰色直接迭代建模在武器故障预报中的应用

黄莹1，2

（1.武警工程大学，西安710086；2.西安交通大学制造系统工程国家重点实验室，西安710049）

摘要：武器系统故障数据常呈现出非等时距、随机性及非准光滑特性，不满足GM（1，1）的建模条件。为此，引入故障信息序列的导数作为建模的白化值，并使用迭代优化算法进行参数优化，从而构建灰色直接迭代GM（1，1）模型。同时，直接迭代建模可有效利用数据第一点的信息，建模时不需累加生成变换和还原处理，算法简单可行，可以有效解决武器系统贫信息状态下的故障预报问题。仿真结果验证了该模型对于实际武器故障序列具有较高的拟合和预测精度。为了解和掌握武器质量状态的发展规律提供了可行的方法。

关键词：非等时距，迭代，灰色模型，武器系统，故障预报

0　引言

武器系统维护是军队装备保障的重点［1］，核心是建立行之有效的故障诊断和预报机制。其中故障预报是提高系统可靠性、避免事故发生的有效途径。

国内外学者对于武器系统的故障预报采用了一些方法。文献［2］将故障预报技术归纳为4类：统计预测技术、数学预测技术、智能预测技术、信息融合预测技术。而这些预测的技术已经在各行各业都得到的应用［3-7］。

但是武器系统的一般造价昂贵，试验费用高，且其故障发生及其发展过程具有不确定因素，欲由大量试验数据评定或预测其可靠性是不太现实的，只能利用有限的试验数据进行系统可靠性评定或预测［1-2］。而灰色系统理论专门针对“小样本、贫信息”进行建模分析，所以将武器系统视为一个灰色系统具有非常好的适用性。利用统计预测技术中的灰色系统理论具有较好的适用性。

灰色预测方法具有预测精度较高、所需历史数据少、不考虑分布规律、运算方便、易于检验等优点。因此，根据数据序列灰色预测理论，可以完成对武器系统历史状态进行趋势分析。通过建立武器各测试参量的灰色预测模型，可以对武器各测试参量的未来状态进行预测，评估武器将可能出现的故障，对其实施预防性的维护，确保武器安全可靠地工作。GM（1，1）模型是灰色系统理论常用的模型，利用GM（1，1）模型进行数列预测，特别是故障数据的预测方面已经取得了广泛的应用［2，6］。但经典的GM （1，1）模型要求原始数据序列是等间隔的，数据序列为准光滑序列，而武器系统故障特征量存在大量的非等时距问题，为此针对非等时距灰色建模方法进行研究。

1非等时距序列建模方法

非等时距灰色建模方法可归纳为两类：一类是对非等间隔序列进行一次累加后，将微分方程近似为差分方程建模求解；另一类是先根据等间隔序列构造出等间隔序列，再利用等间隔序列建模求解。为便于区分，称第1类建模方法为差分模型，第2类为等间隔化模型。

差分模型建模方法在对原始数据序列进行一次累加生成时，又有两种不同的形式，称为一般累加生成差分模型和加权生成差分模型。而从等间隔化模型的建模过程来看，主要区别在于等间隔时间序列的构造上。目前一般都采用最小二乘法和借助平均观测间隔来构造等间隔时间序列。为表示方便，文中以YLCFGM（一般累加差分模型），JLCFGM（加权累加差分模型），DJGHGM1（最小二乘），DJGHGM2（平均间隔）分别代表上述4种模型。

1.1差分模型处理非等距方法

差分模型建模方法在对原始数据序列进行一次累加生成时，又有两种不同的形式，称为一般累加生成差分模型和加权生成差分模型。

对x（0）作一次累加生成，得到生成序列：

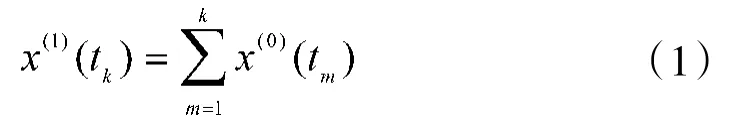
建立生成序列x（1）的微分方程：

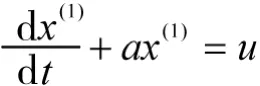
为了得到a和u的估计值，将微分方程用以下差分方程来表示，即：

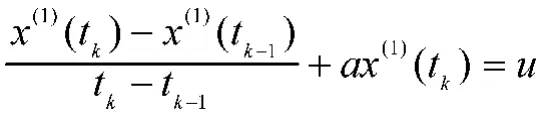
运用最小二乘法得到参数的估计值后，就可得到微分方程的解，即：

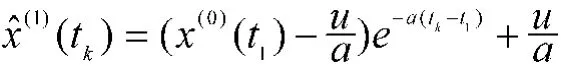
经一次累减还原后，就得到了原始数据序列的模型，即：

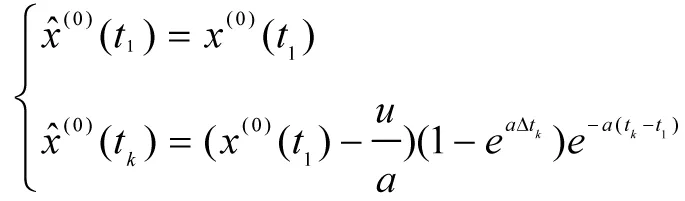
以上就是YLCFGM模型的建立过程。

对于加权生成差分模型而言，设Δt={Δt1，Δt2，…，Δtn}为取样间隔序列，令Δt1=1，Δtk=tk-tk-1，则一次加权累加生成序列为：

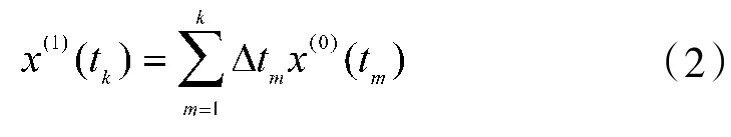
从式（2）可以看出，JLCFGM模型在进行累加生成时，考虑了取样间隔的影响，其余建模步骤同YLCFGM模型。

1.2等间隔化处理方法

从等间隔化模型的建模过程来看，主要区别在于等间隔时间序列的构造上。目前一般都采用最小二乘法和借助平均观测间隔来构造等间隔时间序列。

若采用最小二乘法构造等间隔时间序列，则设对应的时间序列为：t={t1，t2，…，tn}，当Δtk（Δtk=tktk-1）相差不是十分悬殊时，新的时间序列：t'={t1'，t2'，…，tn'}。

时间序列t'（tk'=b0+b1k）就是等间隔时间序列，且需要满足最小。

待定系数：

其中：

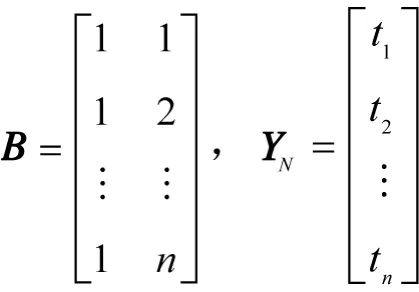
即可得到新的等间隔时间序列。

或者借助平均观测间隔来构造等间隔时间序列，来求平均时间间隔：

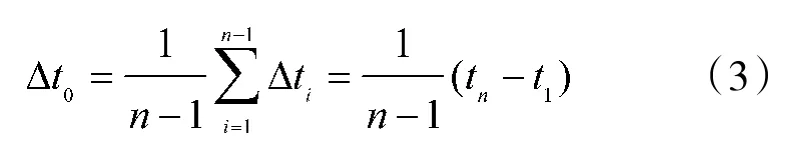
再求各观测周期的时距与平均时距的单位时间差系数：

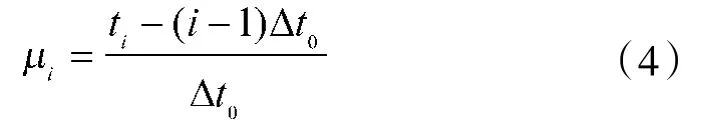
求各观测时期的总差值：

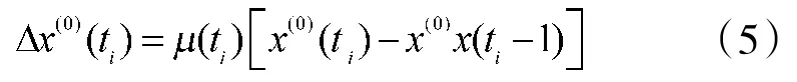
从DJGHGM1模型和DJGHGM2模型的建模过程来看，二者的主要区别在于等间隔时间序列的构造上，DJGHGM1模型采用了最小二乘法来构造等间隔时间序列，而DJGHGM2模型的等间隔时间序列是借助平均观测间隔直接构造的，因此，与DJGHGM1模型相比，DJGHGM2模型的算法得到了简化，减少了计算量。

上述方法实质都是对数据本身进行等间隔化的拟合，而拟合的过程中必然会使测试受到影响，所以需要寻求一种能够直接应用原始数据的方法进行建模。在数学中，求导运算不会影响原始数据的测试。这一点可以作为论文研究的出发点，用原始序列的导数值来构建模型，并对模型进行优化。

2 GM（1，1）迭代优化直接建模

2.1利用导数白化原始信息

GM（1，1）是对具有灰指数律的数据序列［3］：

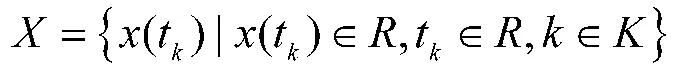
建立指数模型：

建立的一阶线性微分方程模型：

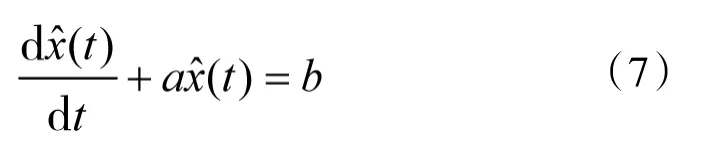
原始数据序列仅给出了某些点的函数值信息，若要直接建模则需要白化信息，可以借鉴高等数学的思想，由函数值的信息结合系统其他信息来间接得到部分导数信息，将其称为灰导数信息。因此，要利用灰色系统理论建立模型就首先要对灰导数信息进行白化。

由拉格朗日中值定理知，若函数x（t）在［tk-1，tk］满足以下条件［8］：

①在［tk-1，tk］连续；

②在［tk-1，tk］可导，则在［tk-1，tk］中至少存在一点ξ，使得

因此，ξ点的导数可以看作是已知的，在区间灰数［tk-1，tk］上，可以认为达到了白化。问题的关键是在［tk-1，tk］区间能够寻求最优的ξ值。

若x（t）在［tk-1，tk］为单调函数，则x（ξ）属于以x（tk-1），x（tk）为端点的开区间，可以得到：

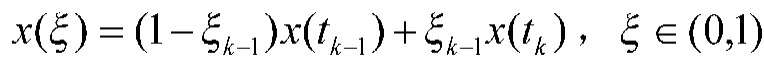
在此，又引入了区间灰数x（ξ），既要利用灰导数增加数据信息，又要利用信息直接建模，要解决的问题就是寻求最优的ξ值，以保证采用中值定理后的数据序列具有白指数律吻合性，符合GM（1，1）直接建模的条件。

2.2非等时距迭代优化直接建模方法

为寻求ξ的优化值，在这里采用数学中的迭代算法，给出初始值，逐步迭代，利用线性回归方法进行参数的辨识。具体步骤如下：

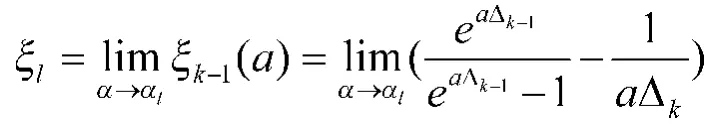
在［tk-1，tk］的白化值为：

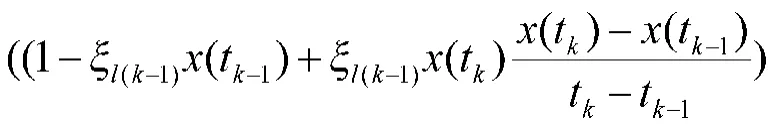
其中l为初始迭代步长，a参数的初始值设定为0。

②利用线性回归对参数的白化值进行辨识：

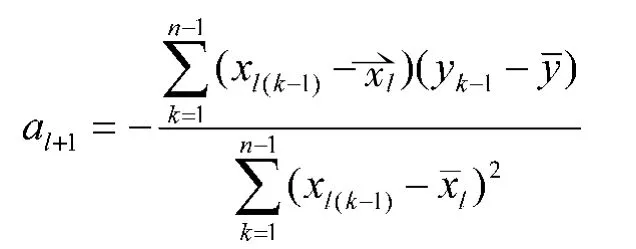
其中

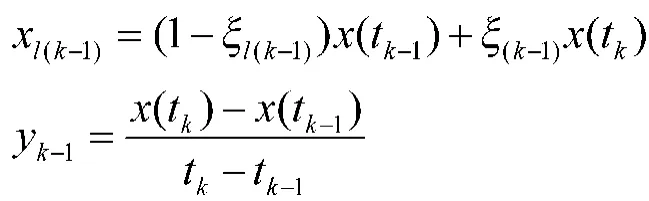
利用线性回归方法得指数模型El+1：

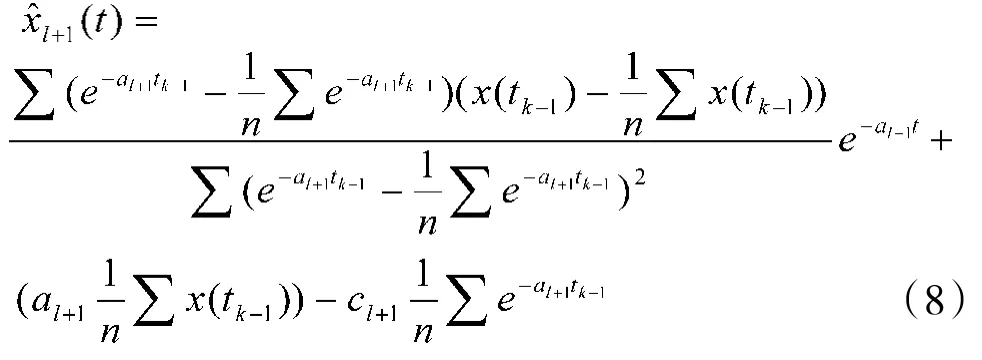
对于模型El+1，用逐步迭代算法优化到满意为止。从以上的建模过程可以看出，利用了原始信息的灰导数信息进行等间隔化，在不影响原始数据的情况下，进行直接建模，而且建模时采用了第一点的信息，采取逐步优化的迭代算法进行参数优化和辨识，称为灰色直接迭代建模方法。

3武器故障预报非等时距灰色预测模型分析

3.1非等时矩差分模型与等间隔化模型分析

武器系统非等时距的故障原始数据如表1所示。

以日期为时间序列，得到序列：

t0=（1，4，11，14，18，21，25，28，32，35，39，42）

很明显，此时间序列为非等间隔时间序列。

对原始数据序列的前8个数据分别建立4种常规模型得到拟合结果如表2所示。再用所建立的模型进行预测，采用原始序列的后4个数据进行预测精度检验，结果如表3所示。

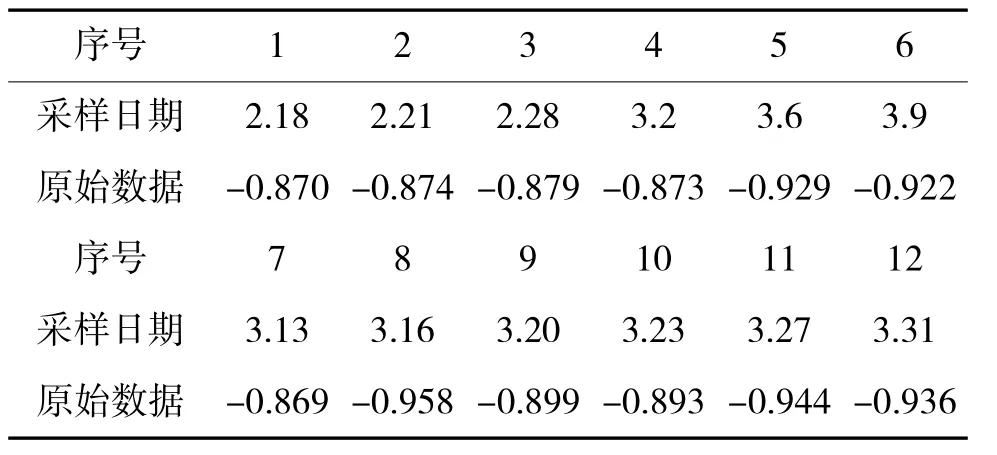
表1　武器系统非等时距的故障原始数据

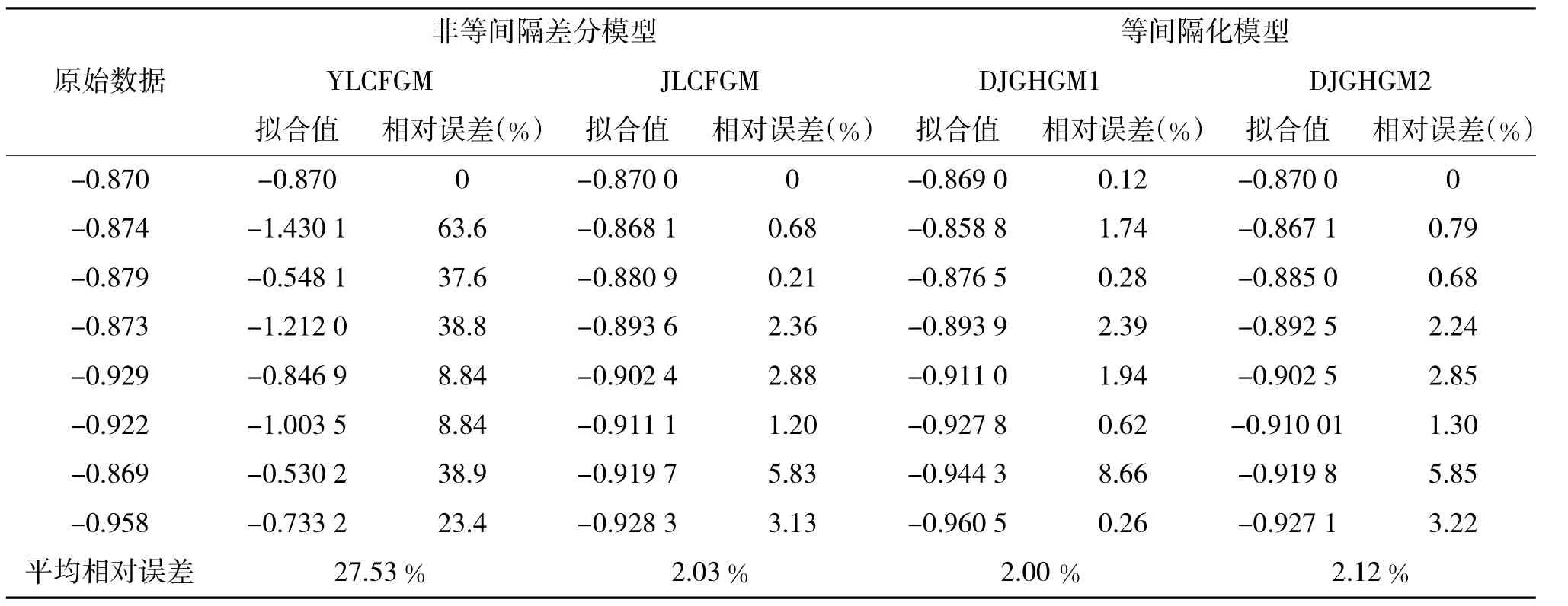
表2　非等时距差分模型与等间隔化模型拟合结果

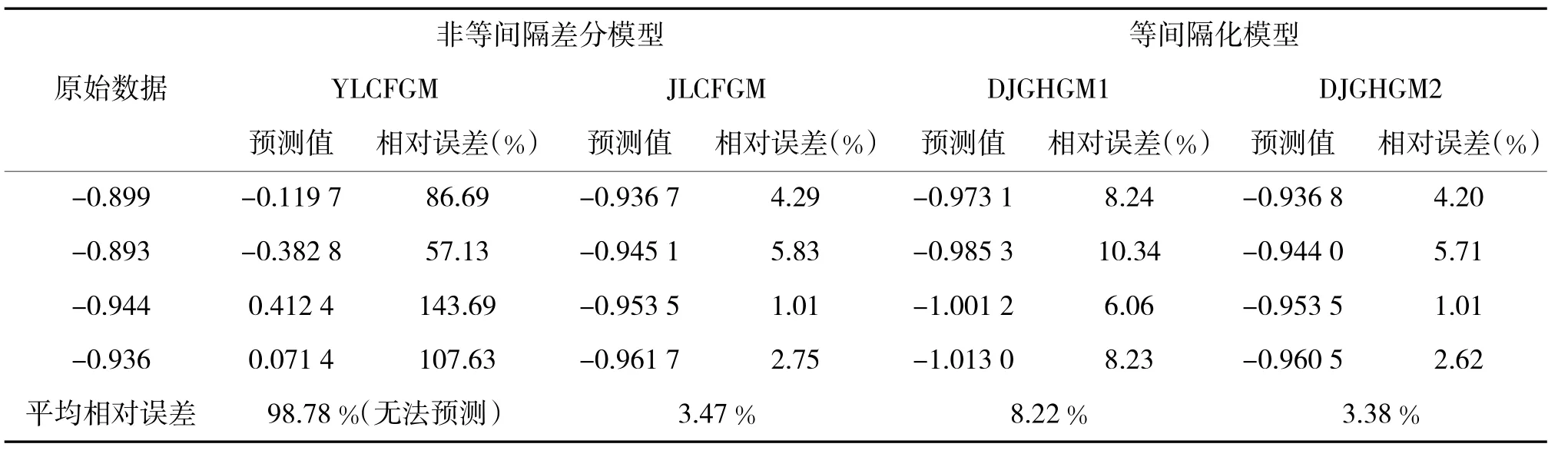
表3　非等时距差分模型与等间隔化模型预测结果

从表2和表3中可以得出结论：基于经典GM（1，1）建模方法的YLCFGM模型拟合精度很低，根本无法用于预测，而JLCFGM，DJGHGM1，DJGHGM2模型都有较好的拟合精度，适于非等间隔序列的建模。

3.2 GM（1，1）迭代优化直接模型分析

利用灰色直接迭代建模法计算灰色拟合模型的优化参数为：

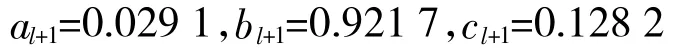
所以其迭代优化灰色预测拟合模型为：

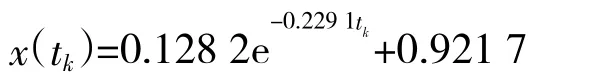
将其拟合的结果列入下页表4所示。

用表2后4个数据进行模型的预测精度检验结果见表5所示。

从表4和表5中可以得出结论：迭代优化直接建模优化法灰色模型对于非等间隔灰色模型具有较高的拟合精度和预测精度，而且它充分利用了第一点的信息，建模时不需累加生成变换和还原处理，具有广泛的适用性。

4　结论

由于现代武器装备系统日趋复杂，使其表现出的故障规律也极其复杂，对装备保障的要求也越来越高。因此，进行装备的预防性维修已经成为部队保障战斗力的一个重要课题，进行故障预报掌握维修的主动权，对充分发挥装备的使用效能，提高战备完好率等方面具有重大意义。

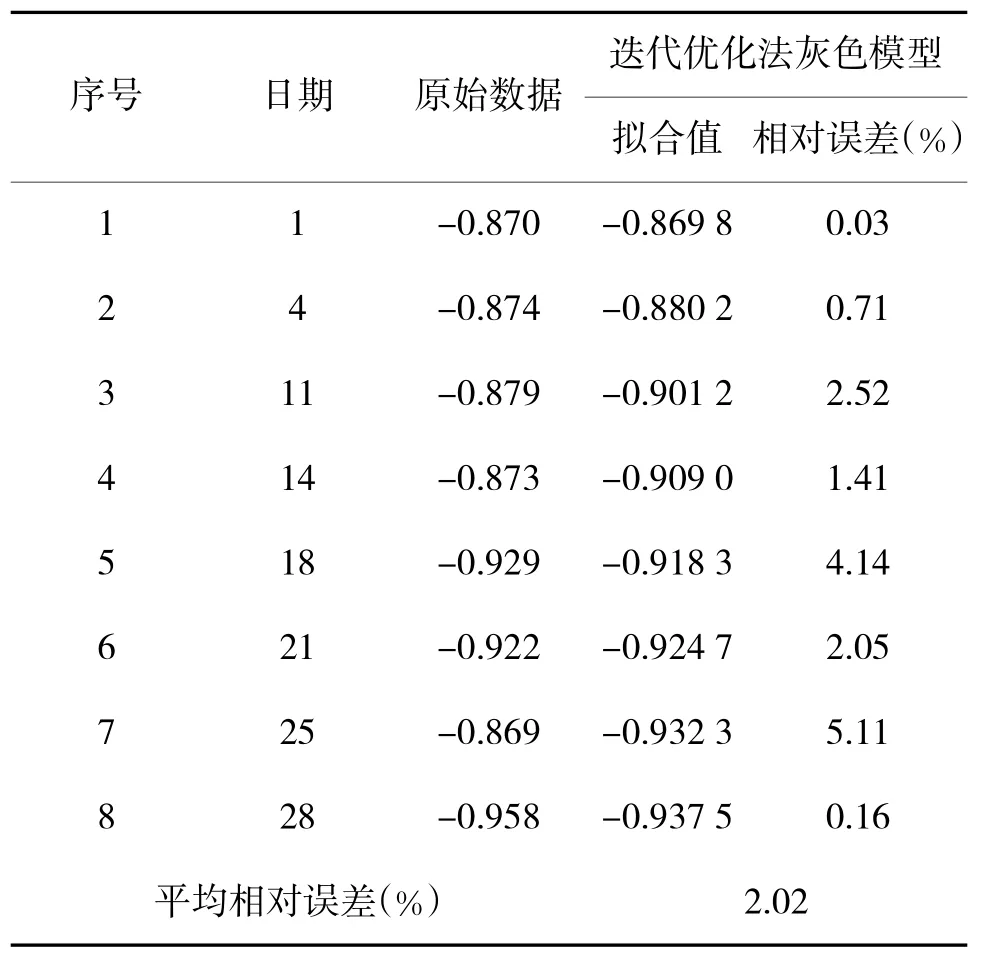
表4　迭代优化法灰色模型拟合结果

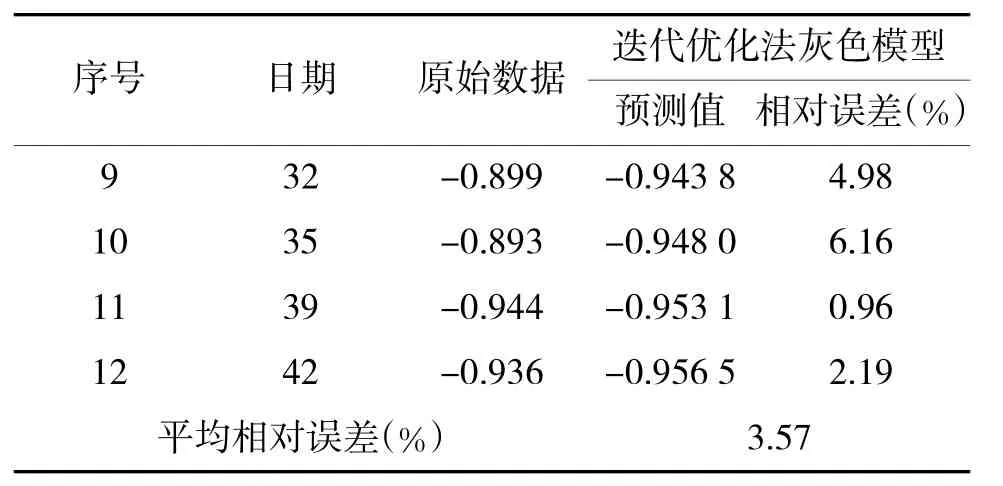
表5　迭代优化法灰色模型预测结果

本文针对武器系统故障数据多为非等时距时间序列的特点，对原有的灰色模型进行改进和优化，提出了原始灰信息白化的一种新的方法，并基于此建立非等时距GM（1，1）迭代优化直接模型，并对该模型进行了理论分析与探讨。

为证明想法的有效性，针对模型进行了仿真，通过实例分析得到了模型的适用范围。结果表明，本文提出的非等时距GM（1，1）迭代优化直接模型具有较高的拟合和预测精度，可以为非等时距的武器系统故障数据序列的建模运算提供方便的工具。

参考文献：

［1］LIU C S，HU S S.Intelligent nonlinear fault diagnosis based on state estimator［J］.Control and Decision，2005，20（5）:557-561.

［2］陆晓鹏.武器装备质量管理和风险管理［M］.北京:海潮出版社，2009.

［3］张光轶，苏艳琴，许爱强.灰色模型在装备故障预测中应用分析［J］.测控技术，2012，31（2）:20-22.

［4］钟洪燕.基于灰色系统理论的宏观经济运行机制及预测［J］.统计与决策，2014，30（1）:145-148.

［5］孟昭渝溪.基于灰色系统理论的传动轴加工质量预测［J］.装备制造技术，2013，10（6）.80-82.

［6］贾得海，曾建初.灰色系统理论GM（1，1）预测模型的应用［J］.昆明理工大学学报（自然科学版），2013，38（6）:115-117.

［7］边培松，王登杰，于少华.新陈代谢GM（1，1）模型在建筑物沉降预测中的应用［J］.山东大学学报:工学版，2010，40（3）:119-123.

［8］王应文.拉格朗日中值定理中间点的渐进性［J］.数学的学习与研究，2013，31（11）:115-118.

［9］李玻，魏勇.优化灰导数后的新G M（1，1）模型［J］.系统工程理论与实践，2009，29（15）:100-105.

［10］刘思峰，谢乃明.基于相似性和接近性视角的新型灰色关联分析模型［J］.系统工程理论与实践，2010，30（5）:881-887.

Application of Non Isometric Iterative Model in the Fault Prediction of the Arms

HUANG Ying1，2
（1.Armed Police Engineering University，Xi’an 710086，China；2.State Key Laboratory for Manufacturing Systems Engineering，Xi’an Jiaotong University，Xi’an 710049，China）

Abstract：Based on the system fault data of weapons for the original time series，aiming at the characteristics of non equal interval，through the establishment of GM（1，1）a whitening method of the original gray information，the gradual iteration of GM（1，1）model is established.Gradual Iteration of direct modeling method makes full use of the first information，modeling without accumulated generating transformation and reduction treatment.This paper using MATLAB simulation，the model has higher for unequal time interval sequence fitting and forecasting accuracy is verified，which provides a new method for understanding and grasping the development law of weapon quality.

Key words：non equal interval，iterative，grey model，fault prediction

作者简介：黄莹（1978-），女，河南渑池人，副教授，博士研究生。研究方向：信息融合、智能控制、导航制导与控制。

收稿日期：2015-03-15修回日期：2015-05-17

文章编号：1002-0640（2016）03-0145-05

中图分类号：TP3

文献标识码：A