一种基于MMMA的双模式变步长盲均衡算法

姜　晖，郭　强

（电子工程学院，合肥　230037）



一种基于MMMA的双模式变步长盲均衡算法

姜晖，郭强

（电子工程学院，合肥230037）

摘要：针对传统修正恒模算法（MCMA）收敛速度慢、剩余码间干扰大的缺点，在双模式修正恒模算法（MCMA+DD-LMS）的基础上引入局部信息量和变步长的思想，提出了一种基于修正多模算法（MMMA）的双模式变步长修正多模算法（VS-MMMA+DD-LMS）。经过理论分析和实验仿真，证明改进后的算法较传统算法具有更好的均衡效果。

关键词：盲均衡，修正多模算法，变步长，双模式

0　引言

在数字通信中，由于传输环境复杂、人为施加干扰等原因，通信信号常会因为信道畸变而产生码间干扰（Inter-symbol Interference，ISI），这严重影响接收信号的质量，降低了通信的可靠性和稳定性。因此，必须使用可靠的均衡技术对信道非理想特性引起的信号失真进行有效校正，以消除或减小ISI的影响，提高通信的质量和效率［1］。盲均衡不需要发射端发送训练序列，可仅利用接收信号对畸变信道进行有效校正，降低传输误码率，是当前飞速发展的数字通信系统中的关键技术之一，应用范围非常广泛［2］。

恒模算法（Constant Modulus Algorithm，CMA）具有计算量小、结构简单、稳健性强等优点，是盲均衡技术中被广泛应用的一种算法，但其存在以下不足：

①易陷入局部极小点，收敛速度较慢；

②收敛后码间干扰较大；

③无法修正信号的相位失真。

为提高传统恒模算法的工作性能，文献［3］提出一种修正恒模算法（Modified Constant Modulus Algorithm，MCMA），通过对误差函数和代价函数进行改进，该算法从根本上实现了对信号相位偏转的修正，但算法在收敛速度和码间干扰方面的改善程度有限。文献［4］则结合判决引导-最小均方误差算法（Decision Directed Least Mean Square，DD-LMS），提出了一种双模式修正恒模算法（MCMA+DD-LMS），它充分发挥了两种算法的优点，极大地提高了均衡效果。本文针对MCMA算法收敛速度慢、剩余码间干扰大的问题，在MCMA+DD-LMS算法的基础上将局部信息量引入到MCMA的误差函数中以减少错误均衡，降低码间干扰；使用切换步长以加快收敛速度。实验仿真表明：改进算法不仅可以消除相位旋转，而且能够加快收敛速度，降低码间干扰，是一种有效的盲均衡算法。

1 MCMA+DD-LMS算法

1.1 MCMA算法

MCMA算法是CMA算法的一种修正形式，该类算法的原理框图如图1所示。

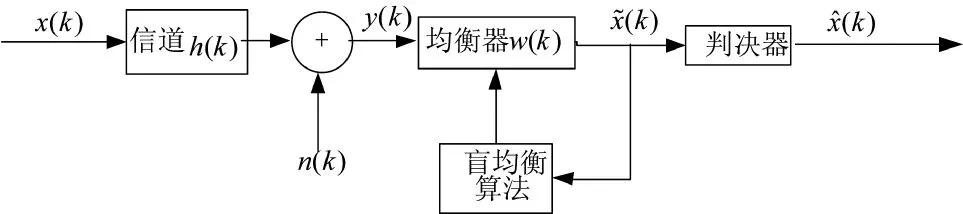
图1　CMA类盲均衡系统基带等效模型

其中，x（k）为发射端经过调制后的信号；n（k）为噪声信号；y（k）为均衡器接收信号；x～（k）为均衡器输出信号；x^（k）为判决器输出信号。

由图1可知：均衡器输出信号

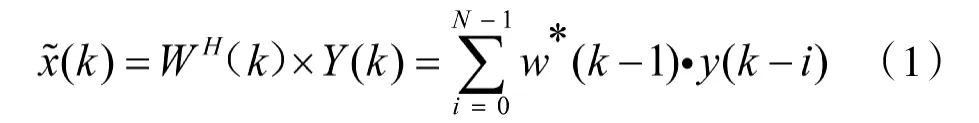
其中，W（k）表示均衡器抽头系数向量，上标‘H’表示共轭转置；w（k）为均衡器抽头系数；N为输入数据总量。

CMA算法中只包含信号的幅度信息，不含相位信息，这致使它对信号的相位变化不敏感，无法对信号通过非理想信道后产生的相位偏差进行补偿，导致输出信号存在不同程度的相位偏移，严重影响了信号的识别和检测［5］。为解决CMA算法无法纠正信号相位失真的缺陷，MCMA算法对输入信号的实部和虚部均进行均衡，其误差函数定义为：

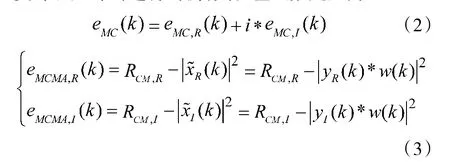
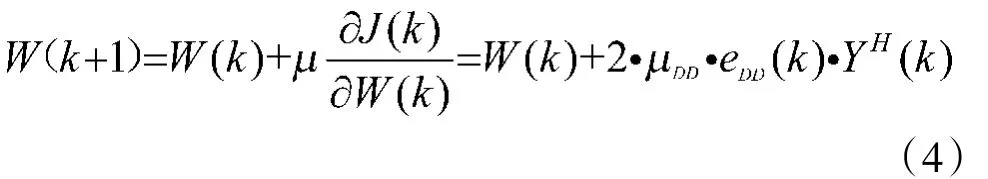
其中，μ表示迭代步长因子，通常取足够小的恒定值。

1.2 DD-LMS算法

DD-LMS是由Lucky在20世纪60年代提出的一种算法，具有收敛迅速、剩余误差小的优点，其误差函数定义为：

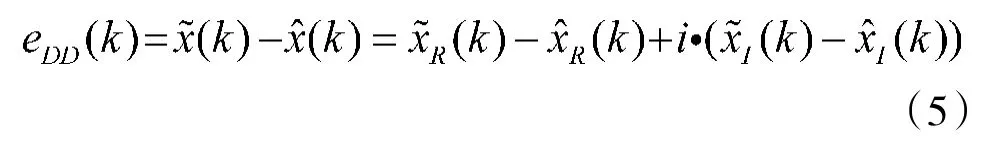
抽头系数迭代公式为：

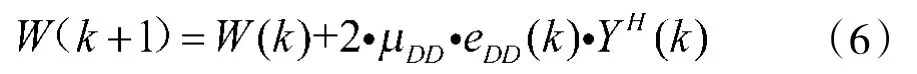
其中，μDD为DD-LMS算法的步长。

1.3 MCMA+DD-LMS算法

MCMA算法具有稳健的收敛性能和重新启动能力，但其收敛速度慢，稳态误差较大；而DD-LMS算法在判决误码率较低时可以迅速收敛且收敛后剩余误差几乎为零，但算法不具备冷启动能力，在误码率较高时极易导致算法发散或误收敛。作为一种双模式算法，MCMA+DD-LMS结合了两种算法的优点，在收敛初期使用MCMA算法作为盲启动算法以降低判决误码率；随着算法的逐步收敛，在误码率降低到一定程度后自动切换到DD-LMS算法以实现快速收敛，提高算法的收敛速度和均衡性能［6］。

MCMA+DD-LMS算法的原理框图如图2所示。

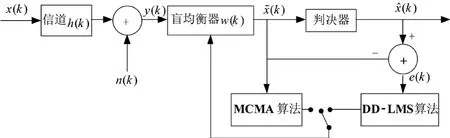
图2　MCMA+DD-LMS算法的原理框图

由图2可知，MCMA+DD-LMS算法的最大特点是可以实现两种算法的切换，而算法合理的切换时机是其拥有良好收敛性能的重要保证［7］：切换过早会导致算法错误判决率较高，甚至无法收敛；切换过晚则无法达到加快收敛的效果。而算法的切换时刻取决于事先设定的切换门限κ，定义：D=|x～（k）-x^ （k）|为判决输出信号x^（k）与均衡输出信号x～（k）的差值的模，当D≥κ时，表示当前时刻算法的误码率较高，算法没有收敛到DD-LMS算法所要求的程度，将继续使用MCMA算法调节均衡器的抽头系数使信号眼图张开；当D＜κ时，表明算法的收敛状态已满足DD-LMS算法的要求，算法会自动切换到DD-LMS算法，以加快收敛速度，减小稳态误差。其中，切换门限κ的取值与均衡输入信号的信噪比有关，设信噪比SNR为：

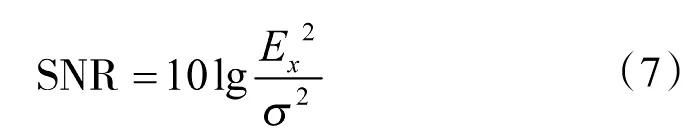
其中，Ex2为信号功率，σ2为噪声功率。由上式可得：

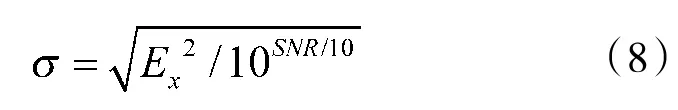
算法要求切换门限κ＜σ，κ可通过多次实验的方法取得最优值。在均衡初期，一部分迭代运算会符合DD-LMS算法的工作要求，而此时判决信号的误码率较高，若使用DD-LMS算法将会增大剩余误差甚至导致算法发散。为解决这个问题，在迭代次数k＜γ时，强制使用稳健的MCMA算法。其中，γ为事先设定的迭代门限。

由以上推导可知，MCMA+DD-LMS算法的抽头迭代公式可表述为：

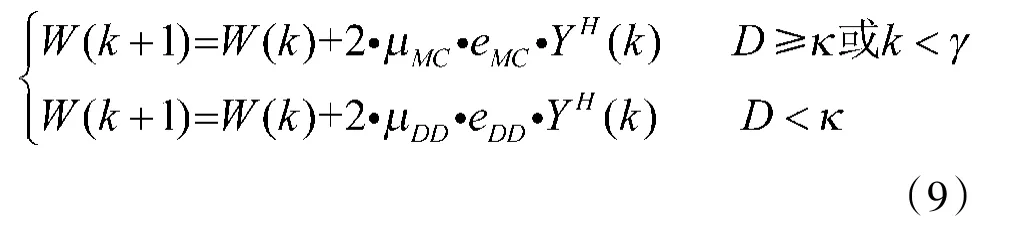
2改进的算法

2.1局部信息量的引入

根据1.1节的分析，MCMA算法试图将信号均衡至一个半径为的圆上。对于恒模信号（如PSK信号）来说，MCMA具有良好的均衡性能；但对于多幅度的MQAM信号来说，由于其信号点分布在多个半径不同的圆上，MCMA算法的均衡效果较差。这主要因为若将PSK信号看作是单一圆（半径为）上的点，而MQAM信号则分布几个半径不一的圆或者矩形之上（例如16QAM信号可看作是分布在3个圆或2个矩形）。

利用局部信息量可以消除具体时刻错误方向均衡的特点，修正多模算法（Modified Multi-mode Algorithm，MMMA）将判决输出信号引入到均衡算法的误差函数中，用判决输出（k）代替恒模算法中的RCM作为期望信号，也就是说MMMA算法不会将信号均衡至一个半径恒定的圆上，而是均衡至多个半径不同的圆上，得到新算法的误差函数如下：

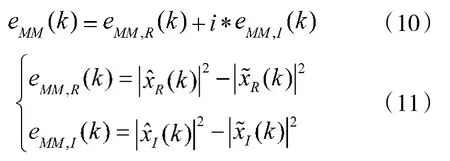
由上式可知，引入局部信息量后，均衡器的输出会与多个模值相吻合，改进后的算法会强制性地将均衡输出靠拢至含有局部信息量x^（k）的星座点上，这就相当于该算法将信号的星座图分为若干区域，在每一区域内都有自己的代价函数，因此可以将代价函数控制在一定的范围，可以有效降低算法收敛后的剩余误差。

2.2变步长思想的引入

在传统恒模类算法中，步长因子为恒定值，无法跟随迭代过程而改变大小，这导致算法收敛速度和收敛精度间存在矛盾，这也是算法收敛速度较慢的重要原因。而变步长的思想因为简单、有效被广泛应用于解决此问题。常用的变步长方法有两类：切换步长法和时变递减步长法，本文用来加快算法收敛的方法为切换步长法。下面将对引入变步长思想的合理性和科学性进行理论分析。

一方面，在算法收敛初期，均衡关心的问题是算法能否收敛，因此希望使用大步长促使算法尽快收敛；而随着算法的逐步收敛，均衡期望获得更好的收敛性能，因此希望步长减小以降低稳态剩余误差，提高收敛精度。变步长的思想可以解决传统恒步长算法中收敛速度与误差之间的矛盾。

另外，根据2.1节的分析可知，MMMA算法的原则为最小化均衡输出～（k）与判决输出（k）的误差。下面将从这一点出发，论证采用切换步长法的必要性和科学性。假设均衡输出信号～（k）与判决信号k）的误差比均衡输入信号y（k）与判决信号x^（k）的误差小，即（k）-（k）|≤|y（k）-（k）|，这说明均衡位于正确的方向上，在抽头系数向量的运算下均衡输出～（k）的模比输入y（k）的模更接近判决输出k），均衡器抽头系数的取值符合算法目标。如果此时再用y（k）去调整均衡器的抽头系数W（k），从统计学角度分析，得到的调整值将会以较大的概率增大算法的代价函数，违背算法的目标。因此，此时应采用较小的迭代步长来调整抽头系数以使系数变化较小。反之亦然，当～（k）-k）|＞|y（k）-（k）|时，表明抽头系数取值不理想，它将一个较为接近（k）的均衡输入信号y（k）调整到较远离（k）的均衡输出信号～（k）。此时，均衡输入y（k）在均衡器抽头系数迭代过程中将发挥较大的作用，应采用大步长以降低代价函数。

同理，当切换至DD-LMS算法时，步长进行切换的原因和条件与上述分析相似。在DD-LMS算法工作时，均衡输出信号～（k）充当训练序列的角色，当～（k）-（k）|≤|y（k）-（k）|时，表明抽头系数W（k）取值较优，符合均衡目标，从统计学的角度分析，应使用小步长以降低代价函数增大的趋势；同理，当|～（k）-（k）|＞|y（k）-（k）|时，应采用较大步长以改变当前的非理想状态，降低代价函数。

根据以上分析可知，变步长思想的引入可以保证在不增加稳态误差的前提下提高算法的收敛速度，提升均衡效果。

综上所述，局部信息量和变步长的引入可以有效提高算法的收敛速度，降低算法的稳态剩余误差，提高算法的可靠性、稳定性和快速性。

2.3新算法的权值更新

根据2.1和2.2节的分析，改进后的VS-MMMA+DD-LMS算法的抽头迭代公式为：

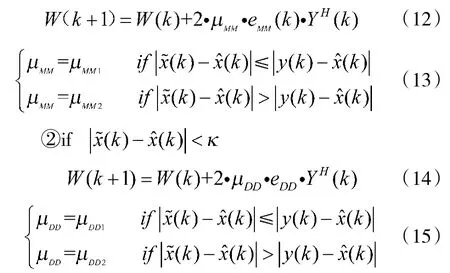
其中，步长因子的大小关系为：μMM1＜μMM2，μDD1＜μDD2。

3实验仿真

3.1仿真条件

为了验证改进算法在数字通信盲均衡中的性能，对VS-MMMA+DD-LMS算法、MMMA+DD-LMS算法和MCMA+DD-LMS算法的收敛速度、码间干扰进行了仿真分析。在仿真实验中，设置的均衡器、传输信道模型和发射信号的参数如下。

均衡器抽头数为15，采用中心化初始策略，即中心抽头系数初始值为1，其他抽头系数初始值取0；信噪比SNR=25 db；σ=0.056，取d=2σ=0.112。

各算法步长初始值设定如下：

MCMA+DD-LMS:μMC=0.000 01，μDD=0.000 04；

MMMA+DD-LMS：μMM=0.000 01，μDD=0.000 04；VS-MMMA+DD-LMS：μMM1=0.000 01，μMM2=0.000 02，μDD1=0.000 04，μDD2=0.000 08。

传输信道为具有严重多径、时延特性的短波通信信道，其冲击响应函数为：

h=［0.05，0.1+0.15i，0.9-0.15i，0.15，-0.2+0.2 i，0.1+0.2 i，-0.1+0.15 i］［10］。

发送信号的调制样式为16QAM，发送符号数为10000；用200次蒙特卡洛仿真的统计平均值来评价几种算法。均衡算法的性能通过剩余码间干扰的大小来评定，其定义为：

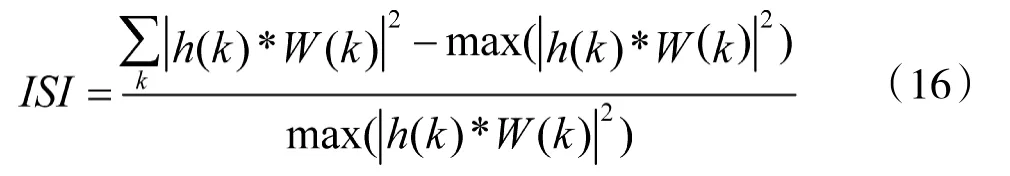
3.2仿真结果分析

图3给出了在信噪比为25 db时，3种算法的均衡性能曲线。由图可知:

①MCMA+DD-LMS算法的码间干扰最严重，均衡性能在3种算法中最差；

②引入局部信息量后的MMMA+DD-LMS算法与MCMA+DD-LMS相比剩余码间干扰有效降低，均衡性能得到了一定提升；

③VS-MMMA+DD-LMS算法由于引入变步长的思想，在经过大约2 000次迭代后便可收敛至-18 db，而MMMA+DD-LMS则要经过5 000余次迭代才可达到相同的收敛状态，由此可见，变步长思想的引入极大地提高了算法的收敛速度。当然，局部信息量和变步长思想的引入略微增加了算法的计算量，但由于高速处理芯片技术的快速发展，增加的计算复杂度不足以影响其硬件的实现。

下页图4、图5为信号经过信道h前后的星座图，可以明显看出发射信号在经过无线多径数字信道后发生了明显的码间干扰，而且产生了相位偏转，导致信号星座图杂乱混沌、难以辨认，严重影响了信号的检测。

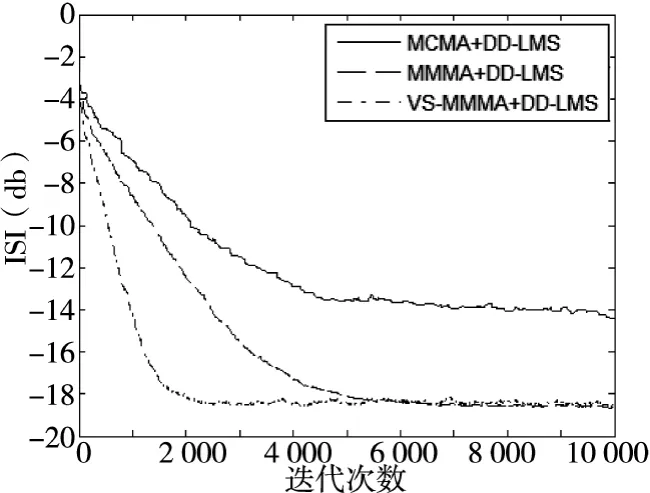
图3　剩余码间干扰收敛曲线

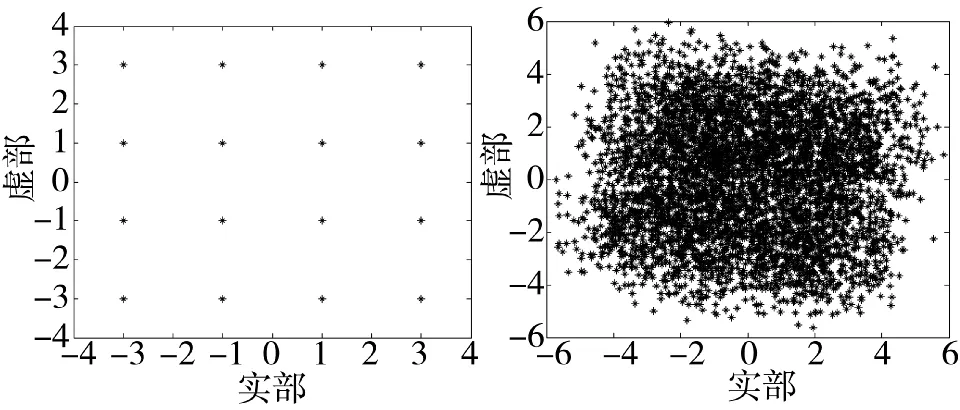
图4　发送信号星座图图　图5　均衡输入信号星座图

图6、图7为信号经过3种算法均衡后的输出信号星座图，由图可知：

①由于信号的实部和虚部同时被均衡，MCMA算法可以有效纠正信道非理想特性造成的相位失真，解决了传统CMA算法均衡后存在相位偏转的缺陷；

②局部信息量的引入，实现了MMMA算法在运算过程中对特定时刻错误均衡的消除，收敛效果更好，因此经过MMMA+DD-LMS、VS-MMMA+DD-LMS算法均衡后的信号星座图不仅无相位偏转而且清晰可辨，集中程度较高，可以较好地实现均衡信号向信源信号的靠拢，性能更加优越。

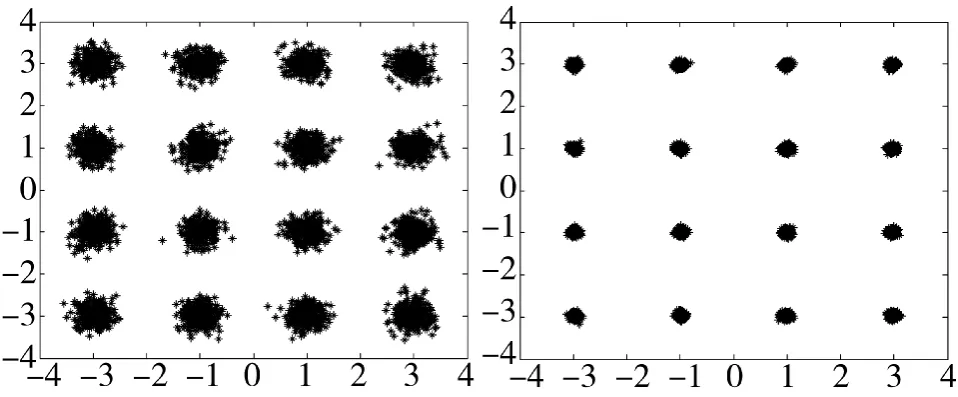
图6　MCMA+DD-LMS均图7　VS-MMMA+DD-LMS衡后信号星座图　均衡后信号星座图

以上仿真实验可以说明，改进后的VS-MMMA+DD-LMS算法相比于传统MCMA+

DD-LMS算法具有更快的收敛速度和更加优越的收敛性能，更有利于获得好的均衡效果。

4　结论

本文在MCMA+DD-LMS算法的基础上，通过引入局部信息量和变步长的思想提出了一种以MMMA算法为核心的VS-MMMA+DD-LMS算法，理论分析表明，新算法不仅可以有效校正信号产生的相位偏差，还可以加快收敛速度，降低剩余码间干扰。实验仿真结果也证明：该算法在收敛速度、剩余码间干扰等方面的性能均优于传统的MCMA+DD-LMS盲均衡算法。

参考文献:

［1］华亚维.短波数据传输自适应均衡技术研究与实现［D］.西安:西安电子科技大学，2009.

［2］杨宾，王大磊，吴瑛，等.利用无约束函数的QAM信号自适应盲均衡方法［J］.信号处理，2014，30（4）:399-404.

［3］RADUNOVIC B，GANTSIDES C，KEY P.Multipath code casting for wireless opportunistic routing［J］.Acm Sigcomm Computer Communication Review，2007，37（04）:169-180.

［4］朱行涛，刘郁林，敖卫东.一种基于MCMA的双模切换变步长盲均衡算法研究［J］.重庆邮电学院学报，2006，18 （6）:690-692.

［5］郝放，闵洁，孙志远.基于MCMA的盲均衡算法［J］.无线电通信技术，2014，40（1）:41-44.

［6］肖瑛，董玉华.并联滤波的常数模与判决引导融合盲均衡算法［J］.声学学报，2012，37（5）:495-500.

［7］董文娟.短波信道盲均衡算法研究［D］.南昌:南昌大学，2009.

［8］ABRAR S.Square-contour stop-and-go algorithm for blind channel equalization in QAM data communication systems ［C］//IEEE Student Conference on Engineering，Science and Technology，2004:73-76.

［9］ABRAR S，AMIN A，SIDDIQ F.Stop-and-go square-contour blind equalization algorithm:Design and implementtation［C］//Proceedings of the IEEE Symposium on Emerging Technologies，2005:157-162.

［10］敖卫东.短波信道自适应盲均衡算法研究［D］.长沙:国防科学技术大学，2007.

A Varying Step Dual-mode Blind Equalization Algorithm Based on MMMA

JIANG Hui，GUO Qiang
（Electronic Engineering Institute，Hefei 230037，China）

Abstract：To solve modified constant modulus algorithm’s problems that it has a slow convergence and has large inter -symbol interference，this paper put forward a varying step dual -mode blind equalization lgorithm based on modified multi-mode algorithm from the introduction of local information and variable step.Through theoretical analysis and experimental simulation，proved that the improved algorithm has better effect compared with traditional algorithm.

Key words：blind equalization，modified multi-mode algorithm，variable step，dual-mode

文章编号：1002-0640（2016）03-0067-05

作者简介：姜晖（1964-），男，安徽合肥人，教授。研究方向：高速数据采集与实时信号处理技术。

收稿日期：2015-03-05修回日期：2015-05-07

中图分类号：TN911.5

文献标识码：A