积分二次相位函数和傅里叶变换的多相码参数估计

胡鑫磊，王春雨，张国毅，田润澜

（空军航空大学，长春　130022）



积分二次相位函数和傅里叶变换的多相码参数估计

胡鑫磊，王春雨，张国毅，田润澜

（空军航空大学，长春130022）

摘要：针对传统时频方法对多相码信号参数估计计算量比较大的问题，提出一种新的多相码参数估计方法。首先利用积分二次相位函数（IQPF）估计信号的调频率，然后重新构造一个线性调频信号（LFM），通过解线调将多相码信号的调频率消除，最后计算解线调后信号的傅里叶变换（FFT）估计信号脊线间隔和载频，进而估计信号的码元宽度和重复周期。该方法不需要进行直角坐标和极坐标的变换且仅需一维搜索，可以大幅度减小计算量。仿真表明，可以用较小的计算量取得与RAT（Radon-Wigner Transformation）和RWT（Radon-Ambiguity Transformation）相当的估计精度。

关键词：多相码信号，参数估计，积分二次相位函数，解线调，傅里叶变换

0　引言

在现代电子战争中，为了免遭敌方电子攻击，提高雷达的生存能力，越来越多的雷达系统采用低截获概率（LPI）信号。由于多相码（Frank、P1、P2、P3、P4码）信号兼具线性调频信号和相位编码信号的优点，已在LPI雷达中广泛应用［1-3］。目前对该类信号的参数估计已成为研究的热点。

多相码信号来源于线性调频信号而且时频特征与线性调频信号相似，目前主要基于对时频平面进行旋转的方法估计多相码信号的参数，RWT和RAT作为两种典型的方法已经在多相码参数估计中的文献中进行了大量分析应用［4-7］。但是这两种变换的计算量比较大，具有较强的噪声基底而且参数估计受角度搜索的分辨率影响较大。为了解决以上问题，本文将LFM信号调频率估计的IQPF方法应用于多相码信号调频率的估计，然后通过解线调思想消除调频率的影响，最后对解线调后的信号进行傅里叶变换估计信号的其他参数。仿真表明当取得与RWT和RAT相同估计精度时，本文方法将二维搜索降为一维且不需要进行坐标变换，具有更小的计算量而且参数估计的精度不受旋转角度分辨率的影响。

1　信号模型

雷达中多相码信号可以表示为：

式中，A为信号幅度；f0为信号载频，为随时间变化的相位码序列，取决于多相码的调制类型。多相码信号主要包括来源于线性调频波形的P3、P4码和近似步进线性调频波形的Frank、P1及P2码，具体表达式参见文献［8］。

图1为理想的P4码进行WVD变换的结果，其他多相码时频图与其类似。

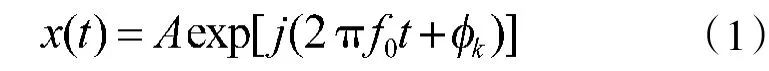
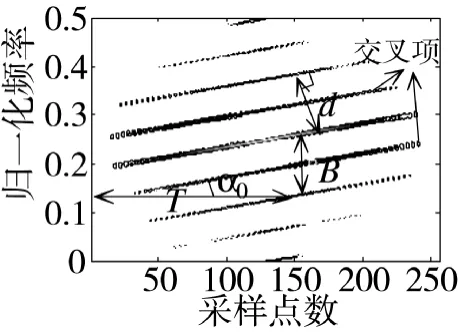
图1　P4码信号的WVD特征

由图1可知多相码的时频图是数条调频率相同的平行直线，能量由主脊线向副脊线依次递减。若脊线与时间轴的夹角为α0，脊线间隔为d，一个编码周期内相位改变Nc次，则多相码信号的调频率k、带宽B、码元宽度Tc及编码周期T的估计值为

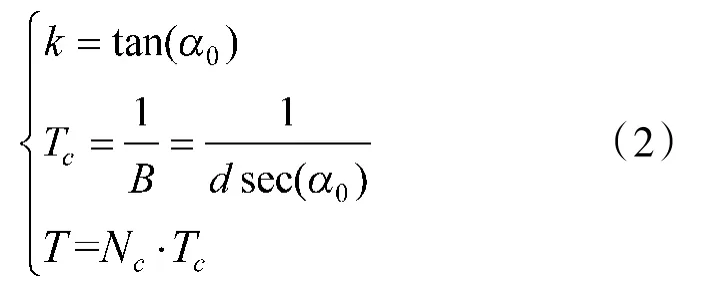
2 LFM信号的IQPF

二次相位函数（QPF）的主要优势是可以将能量集中于信号的调频率曲线上，尤其对单分量LFM信号具有优异的的性能，但是对于多分量LFM信号，互扰比较严重，会产生伪峰［9-10］。而改进的IQPF可以较好地解决多分量LFM信号调频率的估计，而且能够提高参数估计的抗噪性。信号x（t）的IQPF定义为［11］：

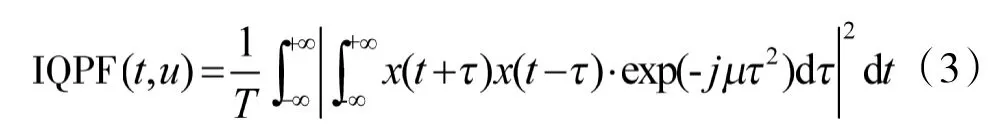
由式（3）可知，IQPF是将QPF函数模平方在调频率-时间平面内沿时间轴做积分，使信号调频率能量得到累积，从而抑制伪峰的影响，提高抗噪性。

已知LFM信号模型为

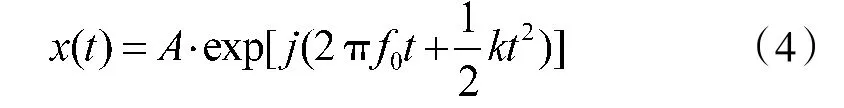
其中，A为信号的幅度，f0为信号起始频率，k为信号的调频率。

将式（4）带入式（3）可得

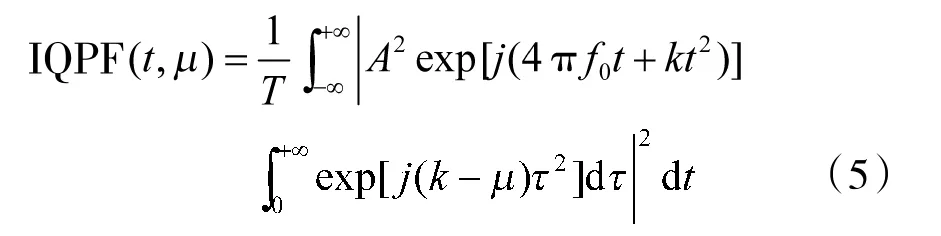
由式（5）可知，LFM信号的IQPF能量峰值在μ=k这一点。图2为单分量和多分量LFM信号的IQPF，由图可知IQPF可以准确估计LFM信号的调频率，对伪峰的抑制能力也比较强，只要检测信号的IQPF峰值即可完成调频率的估计，所以信号调频率的估计值为

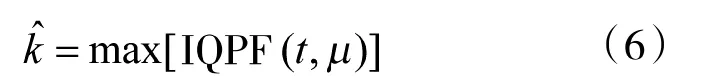
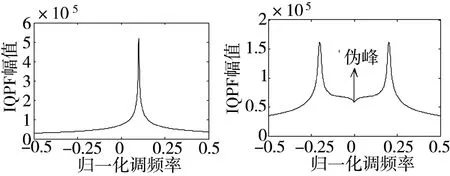
（a）单分量IQPF　　（b）多分量IQPF图2　LFM信号的QPF和IQPF

3多相码信号参数估计

传统方法都是将多相码信号看作LFM信号，基于时频平面旋转搜索峰值找出最大值，从而估计信号的各个参数。但是，这些方法无法同时兼顾参数估计精度与计算量的要求，时频平面旋转角度太小计算量比较大，若搜索角度太大估计精度较差［12］。由第2节分析可知，IQPF仅需一维搜索就可以估计LFM的调频率，且估计的精度不受旋转角度分辨率等人为操作的影响，由于多相码信号的时频特征与多分量LFM信号相似，所以本文首先利用IQPF估计多相码信号的调频率，然后在此基础上对信号进行解线调和FFT，完成其余参数估计。

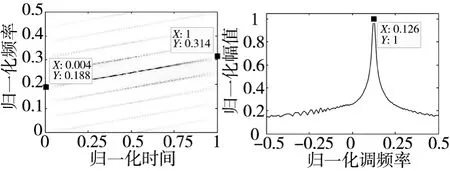
（a）WVD　　（b）IQPF图3　P4码的WVD和IQPF特征

P4信号的WVD和IQPF如图3所示，由图3 （a）可知信号起始点的归一化频率为0.188，终止点的归一化频率为0.314，所以可以计算信号的归一化调频率为0.126，图3（b）可以证实只要检测出IQPF的峰值即可得到P4码调频率的估计值。

得到多相码信号的调频率之后，借鉴快速解线调技术［13］思想构造新的线性调频信号

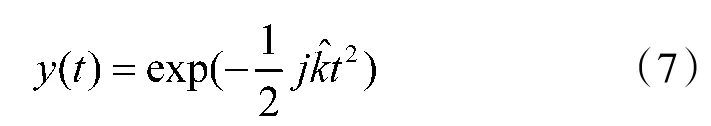
令

由解线调可知，若k^的估计误差较小，c（t）就可以看作是不同频率非调制信号的叠加。图3的P4码经过解线调后的WVD如图4所示，此时时频特征为平行于时间轴的平行直线，且主脊线的频率为原多相码信号主脊线的起始频率，能量由主脊线向两侧副脊线依次递减，主要原因是经过解线调之后已经消除了调频率的影响。

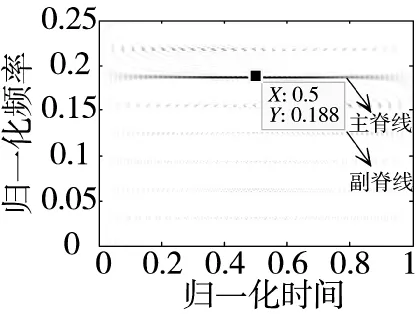
图4　P4码解线调后的WVD特征

由解线调后多相码信号可以看作不同频率的非调制信号的叠加，所以通过FFT计算频谱之后即可估计信号的载频f0。由于多相码解线调后的时频特征也为数条平行直线，所以经过FFT后频谱呈现一系列等间隔的峰值，且主脊线所对应的频谱峰值最大。经过大量仿真证明，P1、P2和P4码解线调之后的时频分布只有一条主脊线，载频对应于时频分布主脊线的中心值，信号的频谱只有一个主峰值，如图5所示，因为这3种多相码信号解线调后的频谱是主脊线的起始频率，所以载频估计需要在频谱估计之后加上主脊线带宽的0.5倍；Frank和P3码解线调之后的时频分布有两条主脊线，载频对应于时频分布起始时间段出现主脊线对应的频率，信号的频谱有两个主峰值，如图6所示，为了判断起始时间段信号的主脊线频率，对这两种信号截取信号的前N/2点（N为信号长度），解线调后计算信号的频谱，载频对应于频谱峰值，如图7所示。而且由图5和图6可知解线调后信号频谱峰值间距即为多相码信号的脊线间隔。

综上分析，多相码信号的参数估计具体步骤如下：

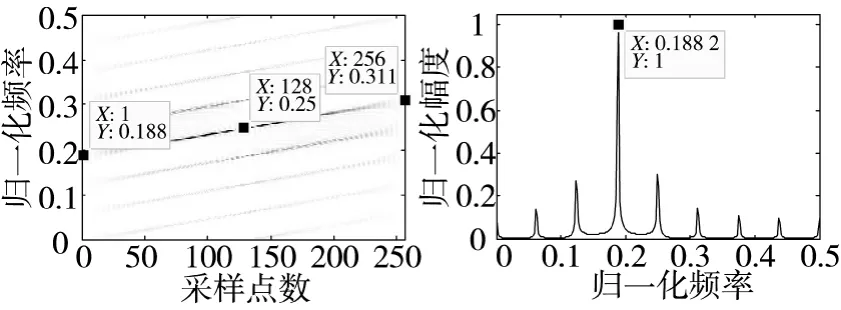
图5　P1/P2/P4码信号的WVD及解线调后的频谱特征

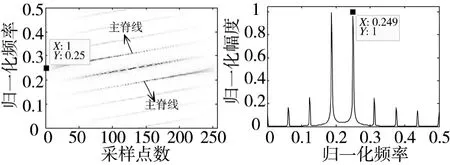
图6　Frank/P3码信号的WVD及解线调后的频谱特征

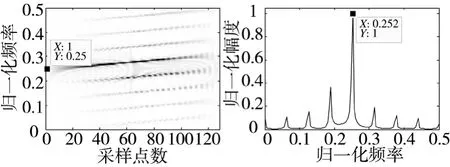
图7　Frank/P3码前N/2信号的WVD及解线调后的频谱特征

①计算信号的IQPF并搜索峰值，估计调频率k；

②按照估计的调频率构造一个调频率为-k，起始频率为0的线性调频信号，利用解线调思想将新的线性调频信号与原多相码信号相乘，得到新信号c（t）；

③通过c（t）的频谱峰值计算脊线间隔。搜索频谱的最高峰值和次高峰值，计算两个峰值的比值λ。搜索所有满足条件的峰值，确定这些峰值所对应的频率fi，计算所有fi的一级差分Δfi，以Δf1为基准剔除误差太大的Δfi，将剩余Δfi的均值作为脊线间隔的估计值d^。若λ＜2判为Frank/P3码信号，搜索阈值为次大值的1/5；若λ＞2判为P1/P2/P4码信号，搜索阈值为次大值的4/5；

④得到脊线间隔的估计值d^之后，依照其和带宽与重复周期的关系求出B和T的估计值B'和T'

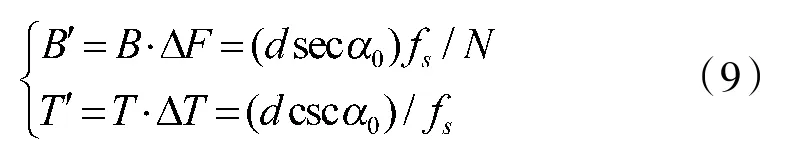
式中，ΔF和ΔT分别为频率轴和时间轴的量化单位，且ΔF=fs/N，ΔT=1/fs；fs为采样频率，N为采样点数。码元宽度Tc=1/B'，一个编码周期内相位改变位数Nc=T '/Tc；

⑤分两种情况计算信号的载频估计值。如果信号为Frank码和P3码，计算前N/2长度信号的频谱，频谱最大值对应的频率即为信号载频的估计值；如果信号为P1、P2和P4码，信号频谱最大值对应的频率加上主脊线带宽的0.5倍即为信号载频的估计值。

4性能分析及仿真实验

4.1计算量分析

将IQPF的计算公式与WVD和AF的计算公式比较可知，IQPF仅比WVD和AF多N次加法和乘法，它们都可以看作自相关之后进行傅里叶变换，计算复杂度均为O（N2·1bN）［11］。由文献［14］可知如果仅仅估计信号的调频率，RAT只需要对过原点直线进行积分，较RWT的计算量要小，但是由于估计多相码的其他参数需要对每条脊线进行积分，所以总体来说RAT与RWT的计算复杂度相当，均为O（N2M）（M为Radon变换旋转角度的个数）。而本文算法只需要计算IQPF之后计算一次解线调（N次乘法）和一次N点FFT，计算复杂度约为O（N· 1bN），所以本文算法计算复杂度小于RWT和RAT。

4.2信噪比分析

由于本文采用顺序参数估计流程，所以IQPF对调频率估计的性能对后面码元宽度和重复周期的估计有重要的影响，输出信噪比SNRout是衡量IQPF估计性能的一个重要指标。假设实际接收的信号为

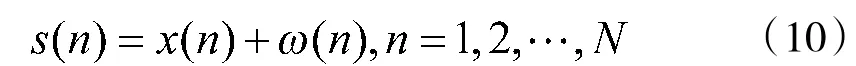
式中ω（n）是均值为0，方差为σ2的高斯白噪声。

定义IQPF的SNRout为

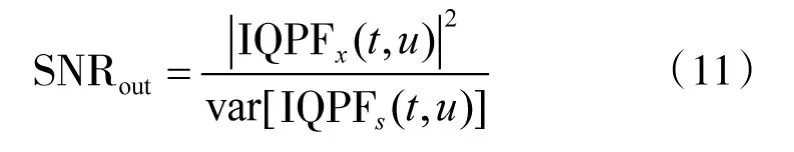
其中，var［·］表示方差。

经过推导文献［15］得到多相码经过IQPF之后的SNRout为

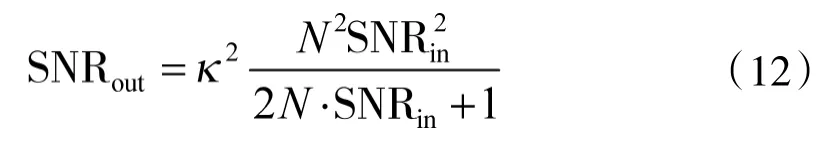
式中，κ为距离主脊线最近的脊线能量与信号能量的比例系数，其值参见表1；输入信噪比SNRin=A2/σ2（A为信号幅度）；N为数据点数。

表1　不同码型的值

由式（12）可知SNRout与信号的SNRin、采样点数N和码型有关，图8为信号点数为256时，不同多相码SNRout与SNRin的关系。由图可知在SNRin相同条件下，Frank码和P3码的比其他3种码型高2dB～3dB，尽管N较小，但是5种多相码经过IQPF之后都可以取得较高的信噪比。所以在低信噪比条件下IQPF对多相码调频率的估计可以满足参数估计的精度，对后续码元宽度和重复周期的估计影响较小。

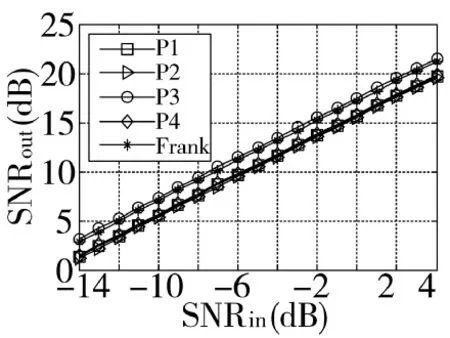
图8　N=256时SNRout与SNRin的关系

4.3仿真实验

为了验证本文算法性能并分析估计精度，对Frank码和P1～P4码信号进行仿真实验。仿真信号参数设置为：码元宽度为tb=0.1 μs，重复周期T=6.4 μs，编码位数为Nc=64，信号载频fc=25 MHz，采样频率fs=100 MHz，所以采样点数为N=640。RWT和RAT的角度分辨率取为0.5°。噪声是均值为0，方差为1的高斯白噪声，信噪比范围取为-14 dB～4 dB，步进为2 dB，每种多相码随机选取100个样本，在每一信噪比下作100次蒙特卡罗仿真实验。

4.3.1不同方法间参数估计性能比较

图9～图11给出了P4码信号的调频率k、码元宽度tb和重复周期T的归一化均方根误差（NRMSE）与信噪比的关系。其中NRMSE定义为

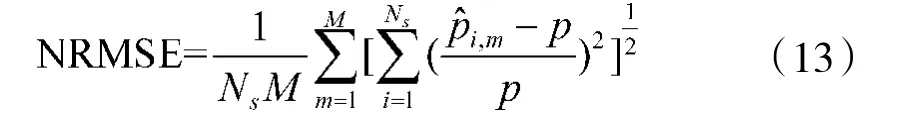
式中，Ns为仿真次数，p为参数的真值，p^i，m为第m个信号样本的第i次仿真的参数估计值。

由于多相码的调频率的克拉美罗下限（CRLB）不易推导，本文利用相同调频率的LFM信号的调频率估计CRLB作为多相码的调频率的CRLB。利用文献［12］中提到的码元宽度和重复周期估计的CRLB作为参照。

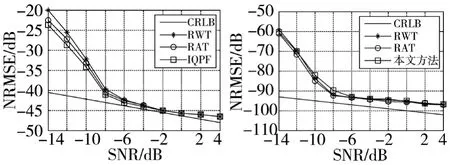
图9　调频率估计性能　图10　码元宽度估计性能

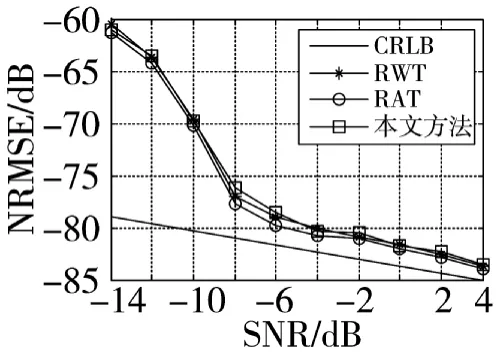
图11　重复周期估计性能

由图9～图11可知本文使用的方法与RWT和RAT对调频率、码元宽度和重复周期的估计具有相当的性能。但是RWT需要进行直角坐标到极坐标的非线性变换和二维搜索，虽然RAT仅需进行一维搜索，但是也需要进行直角坐标到极坐标的坐标变换，而本文方法不需要进行坐标变换，仅需进行一维搜索。所以尽管有相同的估计性能但是本文的方法在计算复杂度方面存在优势。

4.3.2不同多相码间参数估计性能比较

图12～图14是使用本文方法对不同多相码对载频、码元宽度和重复周期估计的NRMSE与SNR的关系，NRMSE的定义式同式（13），其中载频的CRLB采用具有相同载频的非调制信号频率估计的CRLB。

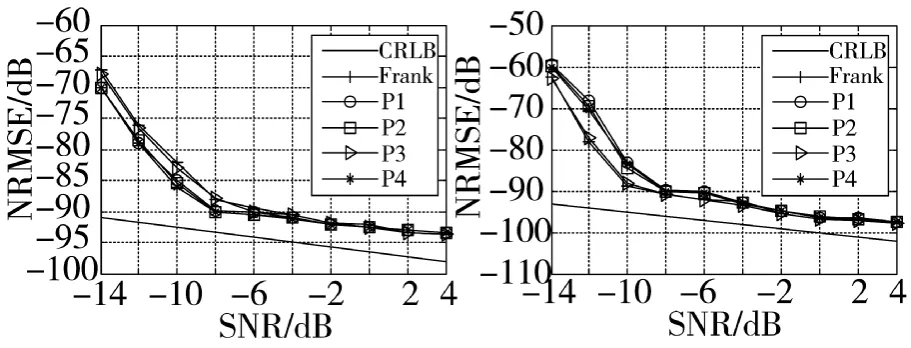
图12　载频估计性能　图13　码元宽度估计性能

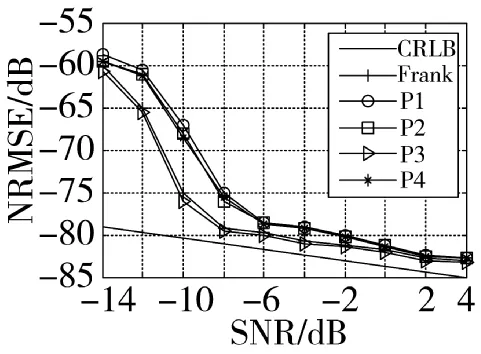
图14　重复周期估计性能

由图12可知，载频估计的SNR门限约为-6 dB。SNR为-14 dB～-6 dB时，进行Frank码和P3码频率估计的NRMSE比其他3种码型大3 dB～5 dB，主要是因为对这两种码型仅仅计算了前半段信号的频谱，使信号能量严重下降，抗噪性比其余3种多相码差，但是随着SNR的提高，5种码型的载频估计性能相当，都能达到-90 dB～-95 dB。由图13和图14可知码元宽度和重复周期估计的SNR门限约为-7 dB。在信噪比较高时，5种多相码的码元宽度和重复周期参数估计的NRMSE相差不大，码元宽度的NRMSE可以达到-90 dB以下，重复周期的NRMSE可以达到-80 dB以下，都比较接近CRLB；在低信噪时，Frank码和P3码频率估计的NRMSE比其他3种码型小5 dB～10 dB，主要因为这两种多相码的次大值较其他码型大，所以脊线间隔估计更加精确，从而可以得到更高精度的码元宽度和重复周期。

5　结论

本文依据多相码信号的时频特征与LFM信号相似的特点，采用了IQPF和FFT对多相码信号进行了参数估计。该方法仅需一维搜索，在与RWT和 RAT的估计性能相当的情况下，该方法计算复杂度小得多。但是仿真表明针对不同的多相码类型，该方法估计性能有一定的差异。对P1码、P2码和P4码的载频估计要优于Frank码和P3码；但是对码元宽度和重复周期的估计Frank码和P3码优于其他3种多相码。总之，本文方法为多相码的参数估计提供了一种新思路。

参考文献：

［1］PACE P E.Detection and classifying low probability of intercept radar［M］.2nd Ed.Norwood，MA:Artech House，2009.

［2］TAYLAN O.GULUM，A，ERDOGAN Y，et al.Elliptic gaussian filtering for time-frequency signal analysis［C］// Radar Conference（RADAR），Ottawa，CA:IEEE，2013.

［3］李宏，陈绍荣，秦玉亮，等.一种多相编码脉压信号的检测与参数估计方法［J］.系统工程与电子技术，2011，33（2）:310-314.

［4］洪先成，张国毅.多相编码雷达信号参数快速估计方法［J］.火控雷达技术，2010，39（3）:28-32.

［5］GULUM T O，PACE P E，CRISTI R.Extraction of polyphase radar modulation parameters using a wigner-ville distribution -radon transform［C］//ICASSP 2009 IEEE International Conference on Acoustics，Speech and Signal Processing.Las Vegas，NV:IEEE，2008.

［6］LI Y X，TANG W W，KUANG Y J.A new polynomial phase signal detection algorithm based on the combination of filter bank and short-time Radon-Wigner transform［C］//2010 IEEE International Conference on Communications and Mobile Computing（CMC）.Shenzhen，CN:IEEE，2010.

［7］王晓峰，张国毅，张旭洲.基于平滑RAT的多相码信号参数估计［J］.电讯技术，2014，54（2）:126-131.

［8］LIN L，LI J.Recognition of polyphase coded signals using time-frequency rate distribution［C］// Processing 2014 IEEE Workshop on Statistical Signal Processing（SSP），Gold Coast，VIC:IEEE，2014.

［9］LI H，QIN Y L，JIANG W D，et al.Performance analysis of parameter estimation algorithm for LFM signals using quadratic phase function［C］// Processing 2009 IEEE International Conference on Wireless Communications & Signal Processing，Nanjing，CN:IEEE，2009.

［10］STANKOVIC S，OROVIC I.Time-frequency rate distributions with complex-lag argument［J］.Electronics Letters，2010，46（13）:950-952.

［11］唐鹏飞，林钱强，袁斌，等.基于积分二次相位函数和分数阶Fourier变换的多分量LFM信号参数估计［J］.信号处理，2012，28（7）:926-931.

［12］李建，张国毅，张旭洲.一种改进的多相码信号参数估计

法［J］.现代防御技术，2013，41（4）:88-93.

［13］XU X B，FAN F F，CAO B L，et al.Parameter estimation of LFM signal based on CAPON and one-dimensional dechirp ［C］//2013 IEEE Region 10 Conference on TENCON，Xi’an CN:IEEE，2013.

［14］徐海源，黄知涛，周一宇.基于Radon变换的具有线性调频特性的多相编码信号参数估计［J］.信号处理，2008，24（2）:172-176.

［15］李宏，秦玉亮，李彦鹏，等.基于AF的多相编码脉冲脉内调制参数估计［J］.系统工程与电子技术，2010，32 （9）:1823-1827.

Parameter Estimation of Poly-phase Coded Signals Based on Integrated Quadratic Phase Function and Fourier Transform

HU Xin-lei，WANG Chun-yu，ZHANG Guo-yi，TIAN Run-lan
（Aviation University of Air Force，Changchun 130022，China）

Abstract：Aim at solve the problem that parameter estimation of poly-phase coded signals has great computation amount for traditional time frequency transformation，a new method is proposed.Firstly，the frequency rate is estimated through using integrated quadratic phase function（IQPF）.Then，a new LFM signal is reconstructed and the frequency rate of poly-phase coded signal is eliminated through dechirp algorithm.Finally，ridge interval and carrier frequency is estimated so as to estimate code width and repeated period.This method doesn’t require conversion rectangular coordinate into polar coordinate and only needs one-dimensional search.So this method can drastically reduce the computation amount.Simulation indicates that its precision of parameter estimation equals to that of RWT’s and RAT’s，consuming less computational amount.

Key words：poly-phase coded signals，parameter estimation，IQPF，dechirp，FFT

作者简介：胡鑫磊（1990-），男，内蒙古呼和浩特人，硕士研究生。研究方向：复杂调制雷达信号的识别。

收稿日期：2015-02-26修回日期：2015-04-28

文章编号：1002-0640（2016）03-0062-05

中图分类号：TN971.1

文献标识码：A