气相爆轰波马赫反射影响因素的实验研究*

刘 杰，杜忠华

(南京理工大学机械工程学院，江苏南京 210094)

1 引 言

爆轰波的马赫反射是一种复杂的非稳态现象，由于它在简单的边界条件下便可容易地发生，因此一直是爆轰物理领域的研究热点。当预混气在Chapman-Jouguet(CJ)爆轰状态下经过收敛通道或圆锥几何体时，存在形成马赫反射的必要条件。马赫反射发生后，接触壁面上为马赫杆。相比于CJ爆轰波，马赫杆的压力和温度陡增，在马赫杆后形成压力和温度更高的过驱爆轰，从而影响马赫杆后反应产物的流场性质。揭示爆轰波马赫反射的传播规律和过驱爆轰的形成机制，既是气相爆轰领域的一个重要课题，也是工程应用领域经常遇到的问题，比如爆轰波在脉冲爆震发动机收敛通道内的传播和尾部喷射的边界控制[1]。因此，掌握爆轰波在收敛通道发生马赫反射时的传播规律具有重要的意义和应用价值。

Akbar[2]选取了3种预混气(即非稳态气体2H2+O2和稳态气体2H2+O2+10.33Ar、C2H2+2.5O2+14Ar)，利用纹影技术得到了清晰的爆轰波马赫反射图像，清楚地分辨出由入射波、马赫杆和反射波组成的马赫反射三波点波系结构(由于实验的初始压力p0较高，因此CJ爆轰波阵面的三波点结构不容易辨别)，测量了马赫反射三波点轨迹角χ，给出了χ与楔角θw之间的实验曲线，尽管与无反应冲击波理论计算结果并不吻合，但是指出了爆轰波本身固有的特征和横波行为对马赫反射的影响。Thomas等人[3]给出了多种预混气的烟膜实验结果以及所测的压力值，但是仅提及过驱度的定义公式，并没有深入研究过驱度与马赫反射的关系及其影响。随后Guo等人[4]同样利用烟膜实验研究了初始压力p0和楔角θw对稳态气体2H2-O2-xAr发生马赫反射的影响，由于氩气高度稀释、当量比为1的氢氧混合气的性质稳定，加之p0和θw的变化范围较小，因此得到p0和θw对马赫反射影响不大的结论。根据上述实验结果，可以明确的是：CJ爆轰波阵面后的平均横波间距大于马赫反射的马赫杆内的横波间距，烟膜实验结果记录了特定研究气体马赫反射胞格结构的变化。数值计算的优势在于能观察每个时间节点的流场特征参数信息，例如：Hu等人[5]对稳态气体2H2+O2+Ar进行了数值计算，详细描述了CJ爆轰波阵面与马赫杆之间的三波点运动及相互作用过程。气相爆轰波数值计算的挑战之一是如何找到以实验为基础、准确的基元反应以及合适的反应速率[6-8]，否则将导致数值计算结果与实验结果在爆轰特征尺度等方面存在一定程度的差异，然而目前的数值计算依然停留在定性分析层面，难以对气相爆轰波的特征进行定量分析。

基于上述尚未解决的问题，我们对典型的稳态气体C2H2+2.5O2+8.17Ar和非稳态气体C2H2+5N2O[9-10]在CJ爆轰状态下的马赫反射进行研究，利用θw与θw+χ之间的关系，探讨马赫反射三波点轨迹与CJ状态下胞格轨迹之间的相互交错行为，分析p0和θw对χ和爆轰波马赫反射过驱度的影响，以及稳态气体和非稳态气体在不稳定性上的差异表现。

2 实验装置及设计

实验装置布局见图1。实验所采用的爆轰管道为矩形截面薄管道，目的是抑制部分爆轰管道厚度方向的横波模态[10]。爆轰管道由驱动段和实验观察段组成。驱动段的截面尺寸为0.100 m×0.025 m，内充初始压力较高的驱动气C2H2+O2。实验观察段中充入所研究的预混气，并放置不同角度的楔面，其截面尺寸与驱动段相同；此外，在放置楔面部位的两侧包夹透明钢化玻璃，为纹影实验提供透光通道。

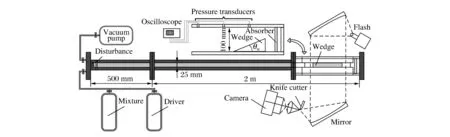
图1 实验装置布局Fig.1 Layout of experimental setup

首先利用18 kV的高压电火花起爆驱动段内的驱动气，过驱爆轰波迅速通过固定在起爆端的双层薄铁纱网，其作用是增加爆轰波的扰动，缩短形成稳定爆轰的距离；随后，稳定爆轰波进入实验观察段，经过楔面后，爆轰波的反应区和激波面被置于实验观察段末端的吸收装置迅速解耦，同时降低反射冲击波的压力，以避免反射波破坏楔面处的烟膜。另外，在爆轰管道侧壁安放PCB-113A24压电传感器，用于测量爆轰波的到达时间和压力。

实验中采用分压法配置预混气体，配气完成后静置24 h，确保气体充分混合。通过改变初始压力p0和楔角θw，以期获得不同初始条件下爆轰波马赫反射实验结果以及p0、θw对爆轰波马赫反射的影响，实验设计见表1。

表1 实验设计Table 1 Experimental design

3 实验结果

3.1 稳定气体C2H2+2.5O2+8.17Ar

图2为C2H2+2.5O2+8.17Ar(p0=5 kPa)经过θw=20°和θw=30°的楔面时爆轰波马赫反射烟膜实验结果。楔面侧面的烟膜记录了三波点运动轨迹和胞格变化过程。由于马赫反射的过驱行为，导致楔面侧面胞格尺寸产生明显差别。图2中的红色虚线近似代表爆轰波马赫反射的三波点轨迹线，轨迹线与楔面之间的夹角即为马赫反射三波点轨迹角(χ)，将马赫反射过程中的胞格划分为CJ区域和过驱区域。由图2可知：过驱区域内的胞格尺寸小于CJ区域；由于CJ区域内的横波随三波点进入过驱区域以及由马赫杆的不稳定性而导致自身产生的横波相互碰撞，使得过驱区域内的胞格较CJ区域内的小而密集，同时，两个区域内横波的相互作用使得马赫反射三波点轨迹线的局部出现波动，根据其总体趋势可测量θw=20°和θw=30°时的三波点轨迹角χ，分别约为14.1°和7.6°；另外，θw=30°时的马赫反射过驱区域胞格尺寸较θw=20°时明显变小，前者的λM/λCJ(马赫反射三波点轨迹线两侧胞格的宽度之比，其中λM为气体经过不同楔角所得到的楔面表面烟膜末端的胞格宽度，λCJ为CJ爆轰下的胞格宽度)约为0.7，而后者的λM/λCJ约为0.5。过驱区域内，胞格由小逐渐增大，说明马赫杆强度逐渐衰减。

图2 C2H2+2.5O2+8.17Ar的烟膜实验结果(p0=5 kPa)Fig.2 Soot tracks of C2H2+2.5O2+8.17Ar at p0=5 kPa

图3为C2H2+2.5O2+8.17Ar(p0=5 kPa)经过θw为20°～40°的楔面时发生马赫反射的纹影实验结果。当θw=20°时，如图3(a)所示，入射波以较小的曲率向马赫杆平缓过渡，马赫反射三波点不易辨别；当θw=30°时，入射波与马赫杆基本相交于一点，存在明显的夹角，入射波的波阵面厚度明显大于马赫杆的厚度；随着θw的增加，马赫杆基本垂直于楔面，马赫三波点逐渐靠近楔面；同时可以清楚地看出马赫反射形成的反射波强度得到增强。

图3 C2H2+2.5O2+8.17Ar的纹影图像(p0=5 kPa)Fig.3 Schlieren photographs of C2H2+2.5O2+8.17Ar at p0=5 kPa

图4为稳态气体C2H2+2.5O2+8.17Ar(p0=5 kPa)经过θw=20°和θw=35°的楔面时的烟迹实验结果。在图4(a)中，在未受马赫反射影响的CJ区域内胞格规则，而在马赫反射形成的过驱区域内胞格小而规则，两者之间的分界线(即马赫反射三波点轨迹线)与楔面的夹角(χ)约为10.1°，λM/λCJ约为0.3。当楔角θw=35°时，如图4(b)所示，马赫反射过驱区域内的胞格尺寸难以测量，轨迹线近似为一条直线，从楔角顶点出发，测得三波点轨迹角约为4.1°；随着初始压力的升高，胞格尺寸λ减小，导致马赫反射三波点轨迹线的波动进一步减小。

3.2 不稳定气体C2H2+5N2O

图5为不稳定气体C2H2+5N2O在不同初始压力下经过θw=30°的楔面所得到的烟膜实验结果。在图5(a)中，C2H2+5N2O具有不规则的胞格结构，由于化学反应剧烈以及波阵面的不稳定性，导致在一些尺寸较大的胞格内存在子胞格结构，说明不稳定气体C2H2+5N2O的横波强度的波动幅度大且运动极不规律；在初始压力较低的条件下，马赫反射三波点轨迹线明显，两侧胞格的差异显著，λM/λCJ约为0.1，χ约为9.7°。随着初始压力的升高，胞格尺寸进一步减小，且更加规则，但马赫反射的表现却不明显，较难辨别出马赫反射轨迹线和过驱区域，如果仅从胞格结构的变化过程来看，马赫反射三波点轨迹线逐渐接近楔面，过驱区域进一步受到压缩。

图5 C2H2+5N2O的烟膜实验结果(θw=30°)Fig.5 Soot tracks of C2H2+5N2O (θw=30°)

图6为C2H2+5N2O在不同初始压力下的纹影实验结果。可以看出：由入射波、马赫杆和反射波组成的马赫反射三波点的结构清晰可见，马赫杆几乎垂直于楔面；在初始压力较小的情况下，CJ爆轰波存在一定的曲率，可观察到波阵面上由马赫杆、横波及前导激波组成的三波点结构；随着初始压力的升高，爆轰波波阵面的波动性逐渐减小，难以区分波阵面上的三波点结构，但马赫反射的反射波却更加明显，说明反射波的强度增强，衰减减慢。

图6 C2H2+5N2O的纹影图像(θw=30°)Fig.6 Schlieren photographs of C2H2+5N2O (θw=30°)

4 实验结果分析

4.1 稳定气体C2H2+2.5O2+8.17Ar

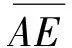
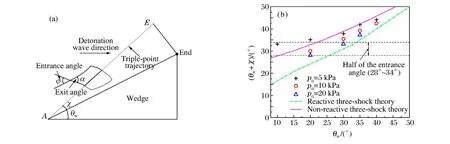
图7 C2H2+2.5O2+8.17Ar的θw+χ与楔角θw的关系Fig.7 θw+χ vs.wedge angle θw in C2H2+2.5O2+8.17Ar

沿楔面方向，利用几何关系，定义爆轰波经过楔角的过驱度MM/MCJ[3]

利用(1)式和冲击波理论，计算得到C2H2+2.5O2+8.17Ar在初始压力为5和10 kPa的条件下过驱度与楔角的关系曲线，如图8(a)所示。可以看出：随着θw的增大，过驱度接近线性上升；实验结果与反应冲击波曲线有一定的差距，更接近无反应冲击波理论值；若楔面长度足够长，马赫杆强度则逐渐衰减，由实验结果所得的过驱度会逐渐向反应冲击波靠近。因此，稳定气体C2H2+2.5O2+8.17Ar在初始压力为5 kPa的条件下经过有限长度的楔面时，爆轰波马赫反射所产生的马赫三波点更接近于无反应冲击波的理论解。

另外，计算得到C2H2+2.5O2+8.17Ar在p0=10 kPa的条件下过驱度与楔角的关系，并与实验结果进行对比，如图8(b)所示。可见，实验结果基本处于两个理论值之间，说明对于C2H2+2.5O2+8.17Ar，随着初始压力的升高，过驱度随楔角的变化趋势逐渐向反应冲击波靠近。对于反应冲击波，由计算可知θw=32.9°是由马赫反射转变为正规反射的临界角；θw>32.9°时，所计算的χ为负值，考虑到余弦函数为偶函数，因此过驱度出现的下降趋势(图8(b)中用虚线框标记)不具有实际的物理意义。然而，对于实验结果，在同样的初始条件下由马赫反射转变为正规反射的临界角要大于40°。

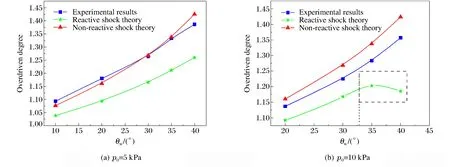
图8 不同初始压力下C2H2+2.5O2+8.17Ar的过驱度与楔角的关系Fig.8 Overdriven degree vs.wedge angle in C2H2+2.5O2+8.17Ar under different initial pressures

图9所示为p0=5 kPa时C2H2+2.5O2+8.17Ar的λM/λCJ与θw之间的关系。可见，λM/λCJ随着θw的增大而基本呈线性下降趋势。

根据Desbordes等人[12]的研究结果，气相爆轰波化学反应诱导区长度ΔI与胞格宽度λ的关系为

式中：D为波阵面速度，ΔI和ΔI,CJ对应不同爆轰波速度下的化学反应诱导区长度，DCJ为CJ状态下的波阵面速度，TvN为von Neumann状态下的温度，Ea为活化能，R为气体常数。对Ea进行无量纲化，得到θ=Ea/RTvN。

式中：τ1和τ2分别对应爆轰速度D1=1.01DCJ和D2=0.99DCJ时定容爆炸点火延迟时间，T1和T2对应爆轰速度为D1和D2时的波后温度[13]。

根据(2)式，可以得到λM/λCJ-MM/MCJ关系的理论解，并与实验结果进行对比，如图10所示。对比可知：当MM/MCJ<1.3时，λM/λCJ的实验数据略高于理论曲线，而当MM/MCJ>1.3时，λM/λCJ的实验结果略低于理论值；尽管实验结果存在一定的测量误差，但是其总体趋势与理论曲线较为吻合。

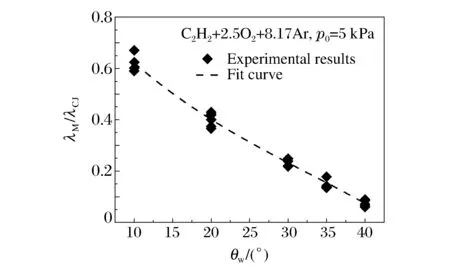
图9 胞格比与楔角的关系(p0=5 kPa)Fig.9 Cell size ratio vs.wedge angle (p0=5 kPa)

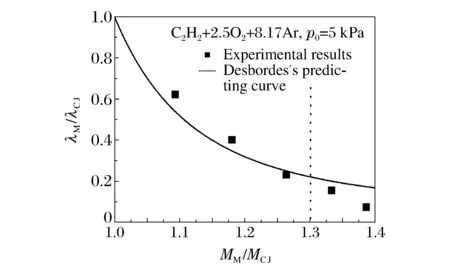
图10 λM/λCJ与MM/MCJ的实验和理论结果对比Fig.10 Experimental and theoretical results of λM/λCJ and MM/MCJ

4.2 不稳定气体C2H2+5N2O

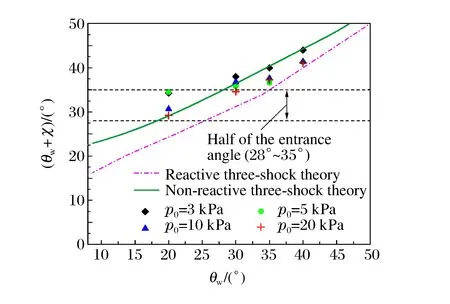
图11 C2H2+5N2O的θw+χ与楔角θw的关系Fig.11 θw+χ vs.wedge angle θw in C2H2+5N2O

对于不稳定气体C2H2+5N2O，可进行类似于稳定气体的分析，在此不再累述，下面仅对不同之处进行分析。C2H2+5N2O的θw+χ与θw及p0的关系如图11所示。当θw=20°时，不同p0下的θw+χ基本高于反应冲击波和无反应冲击波的理论计算值，但均处在胞格入射角的一半以内。因此，在θw较小的情况下，马赫反射三波点轨迹线并不明显；随着θw的增大，θw+χ逐渐高于胞格入射角的一半，马赫反射三波点及其轨迹能更加明显地分辨，并且更接近反应冲击波的理论计算结果。

前文根据胞格结构是否规则作为判断C2H2+2.5O2+8.17Ar和C2H2+5N2O是稳态气体还是非稳态气体的依据，下面将利用爆轰参数来定量描述实验气体的不稳定性。采用Austin等人[13-14]计算预混气爆轰参数的模式，利用ZND模型及CAE程序[15-16]分别计算了稳态气体C2H2+2.5O2+8.17Ar(p0=5 kPa，初始温度T0=298 K)和非稳态气体C2H2+5N2O(p0=3 kPa，T0=298 K)的爆轰参数，结果列于表2，其中pvN为波后von Neumann状态压力。

表2 混合气体爆轰参数的计算结果Table 2 Detonation parameters computed for mixture

Ng[17]基于化学反应机理，给出了用于定量衡量爆轰气体稳定性的参数δ，其表达式为

式中：ΔR为化学反应区长度。δ为无量纲参数，代表爆轰稳定性，δ越大，表示爆轰越不稳定。Ng等人[18-19]认为ΔR可定义为

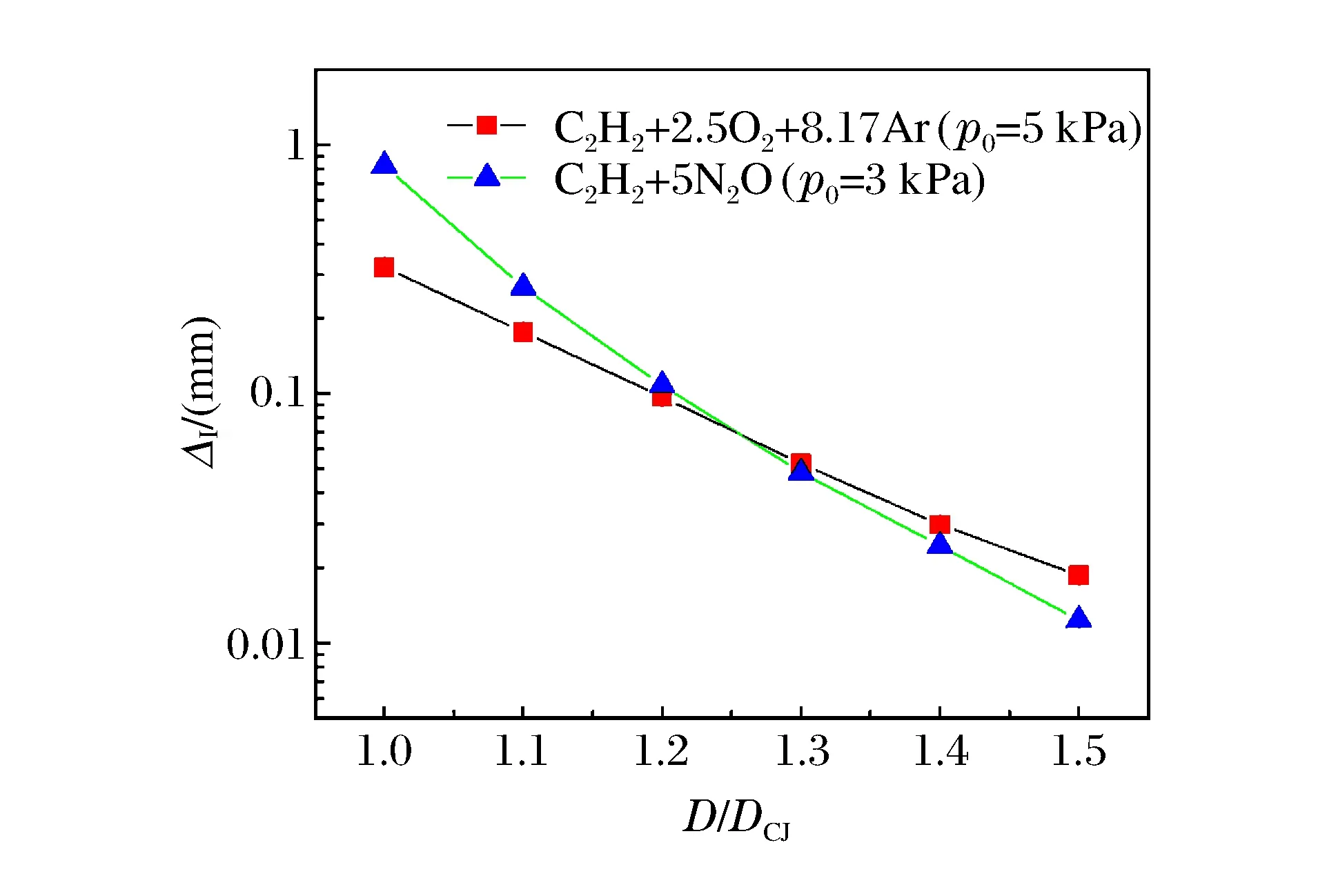
图12 D/DCJ与诱导区长度(ΔI)的关系Fig.12 Incident zone length (ΔI) vs.D/DCJ

根据上述Ng模型，计算得到稳态气体C2H2+2.5O2+8.17Ar和非稳态气体C2H2+5N2O在给定初始条件下的δ，分别为1.4和11.8。对比两种气体的δ可知，C2H2+5N2O的传播不稳定性等级高于C2H2+2.5O2+8.17Ar。

图12为稳定气体C2H2+2.5O2+8.17Ar和不稳定气体C2H2+5N2O的化学反应诱导区长度(ΔI)与速度过驱度(D/DCJ)之间的关系曲线。可以看出：C2H2+5N2O的诱导区长度-速度过驱度曲线斜率的绝对值要高于C2H2+2.5O2+8.17Ar，因此不稳定气体C2H2+5N2O的速度过驱度变化要敏感于稳定气体C2H2+2.5O2+8.17Ar。

5 结 论

无论是稳定气体C2H2+2.5O2+8.17Ar还是不稳定气体C2H2+5N2O，在楔面上都存在胞格由大到小的转变区，转变区之后，马赫反射的马赫杆强度逐渐衰减，胞格由小逐渐增大。楔角θw对稳态气体和非稳态气体的胞格之比λM/λCJ以及χ的影响明显，随着θw的增大，二者的非线性下降，但θw+χ的值却逐渐上升，因而θw越大，爆轰波马赫反射越明显；当初始压力较低时，爆轰波马赫反射中的χ和θw靠近无反应冲击波理论计算结果，随着初始压力的升高，χ和θw二者的实验关系逐渐向反应冲击波理论计算结果接近。计算的爆轰参数表明：不稳定气体C2H2+5N2O的不稳定参数δ大于稳定气体C2H2+2.5O2+8.17Ar，即前者的不稳定性高于后者；此外，前者的诱导区长度-速度过驱度曲线斜率的绝对值明显高于后者，说明不稳定气体C2H2+5N2O对速度过驱度DM/DCJ更加敏感。

[1] 王 栋.脉冲爆震发动机工作过程数值模拟研究 [D].南京:南京理工大学,2007:3-26.

WANG D.Numerical simulation of pulse detonation engine cycle [D].Nanjing:Nanjing University of Science and Technology,2007:3-26.

[2] AKBAR R.Mach reflection of gaseous detonations [D].Troy,USA:Rensselaer Polytechnic Institute,1997.

[3] THOMAS G O,WILLIAMS R LI.Detonation interaction with wedges and bends [J].Shock Waves,2002,11(6):481-492.

[4] GUO C M,ZHANG D L,XIE W.The mach reflection of a detonation based on soot track measurements [J].Combust Flame,2001,127(3):2051-2058.

[5] HU Z,JIANG Z.Wave dynamic processes in cellular detonation reflection from wedges [J].Acta Mechanica Sinica,2007,23(1):33-41.

[6] 张德良,谢 巍,郭长铭,等.气相爆轰胞格结构和马赫反射数值模拟 [J].爆炸与冲击,2001,21(3):161-167.

ZHANG D L,XIE W,GUO C M,et al.Numerical simulation of cellar structures and Mach reflection of gaseous detonation waves [J].Explosion and Shock Waves,2001,21(3):161-167.

[7] 胡宗民,高云亮,张德良,等.爆轰波在楔面上反射数值分析 [J].力学学报,2004,36(4):385-392.

HU Z M,GAO Y L,ZHANG D L,et al.Numerical simulation of gaseous detonation over wedges with a detailed chemical reaction model [J].Acta Mechanica Sinica,2004,36(4):385-392.

[8] WANG C J,GUO C M.On the influence of low initial pressure and detonation stochastic nature on Mach reflection of gaseous detonation waves [J].Shock Waves,2014,24(5):467-477.

[9] LEE J H S.Dynamic parameters of gaseous detonations [J].Annu Rev Fluid Mech,1984,16:311-336.

[10] LEE J H S.The detonation phenomenon [M].New York:Cambridge University Press,2008.

[11] LI H,BEN-DOR G,GRÖNIG H.Analytical study of the oblique reflection of detonation waves [J].AIAA J,1997,35(11):1712-1720.

[12] DESBORDES D.Transmission of overdriven plane detonations:critical diameter as a function of cell regularity and size [J].Prog Astronaut Aeronaut,1988,114:170-185.

[13] AUSTIN J M.The role of instability in gaseous detonation [D].Pasadena,California:California Institute of Technology,2003.

[14] PINTGEN F,ECKETT C A,AUSTIN J M,et al.Direct observations of reaction zone structure in propagating detonations [J].Combust Flame,2003,133(3):211-229.

[15] MCBRIDE B J,GORDON S.Computer program for calculation of complex chemical equilibrium compositions and applications Ⅱ:user’s manual and program description:NASA RP-1311-P2 [R].Washington D C:National Aeronautics and Space Administration,1996.

[16] SHARPE G J.Transverse waves in numerical simulations of cellular detonations [J].J Fluid Mech,2001,447:31-51.

[17] NG H D.The effect of chemical reaction kinetics on the structure of gaseous detonations [D].Montreal,Canada:McGill University,2005.

[18] NG H D,RADULESCU M I,HIGGINS A J,et al.Numerical investigation of the instability for one-dimensional Chapman-Jouguet detonations with chain-branching kinetics [J].Combust Theory Model,2005,9(3):385-401.

[19] NG H D,HIGGINS A J,KIYANDA C B,et al.Nonlinear dynamics and chaos analysis of one-dimensional pulsating detonations [J].Combust Theory Model,2005,9(1):159-170.