高压下钼的声子色散的改进分析型嵌入原子法研究*

张晓军，王安祥 ，高 宾，陈长乐

(1.西安工程大学理学院，陕西西安 710048; 2.西北工业大学陕西省凝聚态结构与性质重点实验室，陕西西安 710072)

1 引 言

声子色散关系是研究固体材料物理性质如比热、热导、超导、声速、声-电相互作用的重要信息[1]。此外，高压下声子谱中的负频模式是评判固体材料结构相变的重要依据[2]。因此固体声子色散关系的实验和理论研究一直吸引着众多科研工作者[3-4]。对于金属或合金在常压下的声子色散关系已存在大量的实验和理论研究结果。近年来，人们趋于对特殊条件下(如高温和高压)声子色散的研究。实验方面，把金刚石压砧技术和非弹性X射线散射技术或非弹性中子散射技术相结合来测量高压下固体的声子色散关系[5-6]。另一方面，试图从理论上重现这些实验结果或预言高压下的声子色散关系。Fang等[7]利用密度泛函理论在准谐和近似下计算了压强分别为23和55 GPa时金属铱沿对称方向上的声子谱。Hu等[8]利用第一原理计算了不同压强下金属钛Ti沿4个对称方向的声子色散曲线。这些方法物理意义深刻、明确且能提供原子间相互作用的精确信息，在计算金属和合金的声子色散关系方面也非常成功。但是这些方法要求计算机有相当大的计算能力，而且需要花费相当多的计算时间。同时，由于计算局限性，该方法最多只能处理上百个原子的系统，往往不能高效地描述实际的材料结构,尤其对于复杂的体系难以普遍应用。由于这些原因，研究人员开始着手利用经验多体势模型来研究高压下的声子色散关系。与第一原理计算相比，经验多体势模型能够快速提供原子或分子间的相互作用信息，且能处理几千甚至上万个原子的庞杂系统。Kazanc等[9]曾利用经验多体势即Sutton-Chen式嵌入原子法(SCEAM)计算了不同压强下镍钯无序合金沿[100]、[110]和[111] 3个高对称方向上的声子色散曲线。我们也曾用张邦维等发展的改进分析型嵌入原子法(MAEAM)模拟了高压下金属铜沿3个高对称方向和4个低对称方向上的声子色散曲线[10]。然而，这些结果都没有相应的实验数据相佐证，难于说明经验多体势是否能合理描述高压下原子间的相互作用。本研究把张邦维等发展的改进分析型嵌入原子法模型与晶格动力学理论相结合，模拟高压下金属钼(Mo)沿3个高对称方向上的声子色散曲线，并和对应的实验结果进行比较。

2 改进分析型嵌入原子法模型

在重现或预测固体材料声子色散关系的计算中，原子之间的相互作用势是必不可少的。经常采用的两体势有Morse势[11]和Murrell Sorbie势[12]，多体势模型有密度泛函理论(DFT)[13]、嵌入原子势模型(EAM)[14]和紧束缚理论(TBT)[15]等。其中，由Zhang等[16-17]发展的改进分析型嵌入原子法模型已成功地计算了面心立方金属的界面能[18]、晶界能[19]以及体心立方金属的空位迁移能[17]等。改进分析型嵌入原子法的基本公式为[16-17]

式中:Et是系统的总能量，F(ρi)是在除第i个原子外的其他原子组成的基体中再嵌入第i个原子的嵌入能，仅是其他原子在第i个原子所在处产生的背景电子密度ρi的函数，其中f(rij)为单个孤立原子的球型电子密度分布函数，rij是第i个原子和第j个原子间的距离；φ(rij)是第i个原子和第j个原子间的相互作用能；M(Pi)是修正项，表示原子电子密度非球型对称分布所引起的系统总能量的变化。嵌入函数F(ρi)、原子间的相互作用势φ(rij)、修正项M(Pi)和电子密度函数f(rij)采用如下形式[16-17]

式中:下标“e”表示平衡状态，re表示在平衡状态下纯元素晶体中原子的最近邻距离，其他模型参数如F0、n、α、ks(s=-1～4)见表1。

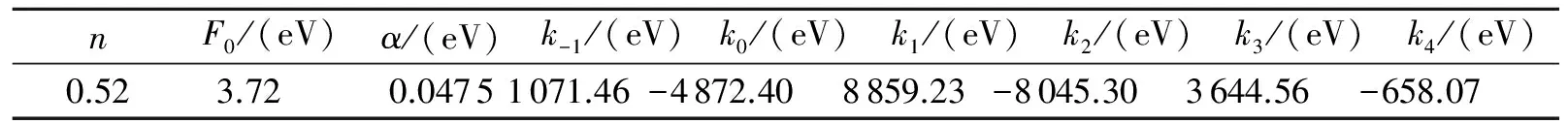
表1 金属钼的模型参数Table 1 The model parameters of metal Mo

3 晶格振动模型

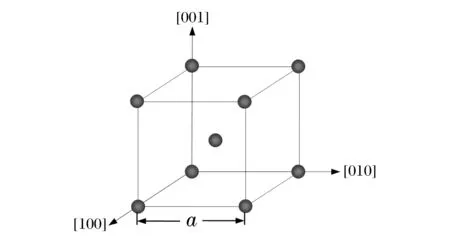
图1 体心立方晶体结构 Fig.1 Bcc crystal structure

常温常压下，金属钼属体心立方结构，其晶体结构如图1所示，晶格常数为a。在晶体结构中设坐标原点处的原子为参考原子n，根据晶格动力学理论[20]，参考原子n的振动方程为

(8)

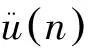
(9)

求解(8)式，可得

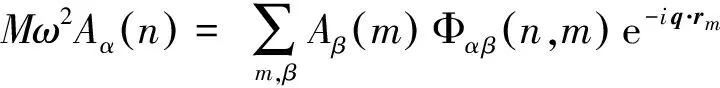
(10)

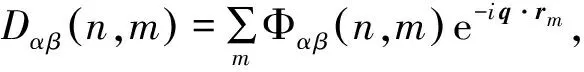
(11)

显然，(11)式是A(n)的3个线性齐次方程，因为晶格振动总是存在的，故A(n)有非零解的条件是

|Dα β(n,m)-δα βω2(q)|=0

(12)

通过联立(1)式、(9)和(12)式，就可以得到体系的振动频率ω(q)和波矢之间的关系，即声子色散关系。

4 模拟方法和结果分析

在晶格动力学理论和改进分析型嵌入原子法的框架下，采用数值计算的方法模拟了高压下金属钼的声子色散曲线。在模拟过程中，选取8a×8a×8a的晶块作为模拟单元，其中包括坐标原点在内的4a×4a×4a晶块作为内部单元，其余原子为外部单元，外部单元是为了确保内部单元边界处和近边界处的原子周围有足够多的近邻原子与之相互作用，同时假设所有的原子满足三维周期边界条件。选取对势函数的截止距离为0.626 nm，应用Matlab语言编辑计算机程序计算参考原子与其他原子之间的原子力常数和动力学矩阵元，把这些值代入久期方程((12)式)获得不同波矢所对应的声子频率值，具体的计算细节可参考文献[21]和文献[22]。在计算不同压强下的声子色散关系时，采用Rose-Vinet[23-24]方程来控制加载在体系上的静压力。根据Rose-Vinet方程，金属钼的压强和压缩的关系可表示为

(13)

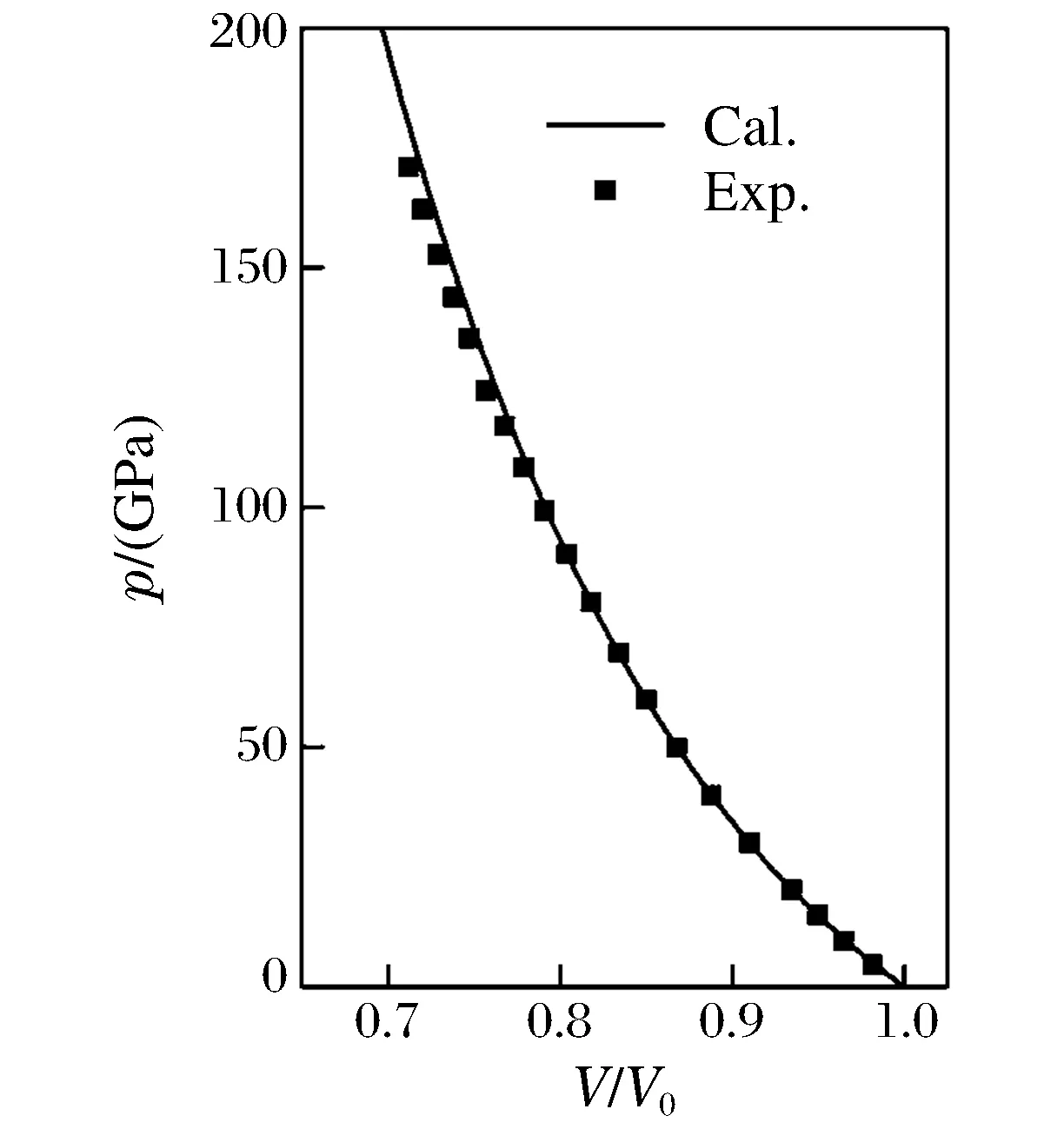
图2 金属钼的压强和体积间的关系 Fig.2 Pressure versus volume for Mo

由MAEAM模型所计算的压强分别为0.1 MPa、17 GPa和37 GPa时金属钼沿[00ζ]、[0ζζ]和[ζζζ] 3个高对称方向的声子色散曲线如图3、图4、图5所示，其中实线为模拟值，实心圆点为实验值[26-27]，群论符号Γ、H、P′、P和N表示体心立方晶格布里渊区中的不同对称点，符号L和T分别表示纵振动模和横振动模，ζ=q/qmax是简约波矢。根据晶格动力学理论，体心立方布拉菲晶胞会产生3个声子振动支，其中2个为横波声学振动支，1个是纵波声学振动支，由于四重和六重轴对称性，2个横波声学振动支往往会在某些振动方向上兼并为1个横波振动支，如图3、图4、图5所示，这些图像和现在的计算结果相符合。从图3可以看出，在常压下(0.1 MPa)，我们的计算结果整体上和实验结果相一致，包括一些布里渊边界点，例如T[00ζ]和L[00ζ] 振动支中的H点，T1[0ζζ]和T2[0ζζ]振动支中的N点。在L[00ζ]振动支中简约波矢ζ在0.3～0.6之间，T[ζζζ]振动支中ζ在0.3～0.9之间，L[0ζζ]振动支中ζ在0.3～0.5之间。计算结果与实验结果在数值上有些偏差，但所对应色散曲线的形状却非常相似(图3)。压强p=17 GPa时，色散曲线的理论计算实线和实验点线整体一致，特别在低频附近(图4)。与常压下声子色散曲线相比，在压强为17 GPa时的色散曲线中，频率偏差主要出现在T[00ζ]和L[00ζ]振动支中的H点、T[ζζζ]和L[ζζζ]振动支中的P点以及T1[0ζζ]和L[0ζζ]振动支中的N点附近，最大偏差不超过10.8%。压强p=37 GPa时，L[00ζ]振动支的色散曲线和实验结果基本吻合，其他方向上色散曲线的形状和常压以及17 GPa时的结果非常相似，只是频率略有上移，遗憾的是只有L[00ζ] 振动支的实验结果与之相比较，而缺少其他振动支的实验数据。从上面的分析可看出，我们的计算结果均与实验结果基本吻合，只是数值上有较些差异。考虑到计算结果是在谐和近似下所得，而实验结果并不能忽略非谐和效应，因此二者之间存在差异是合理的。这表明MAEAM模型可以合理描述常压和高压下原子之间的相互作用。

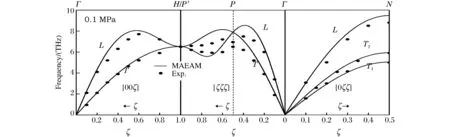
图3 常压下钼的声子色散曲线 Fig.3 Phonon dispersion curves of Mo under normal pressures

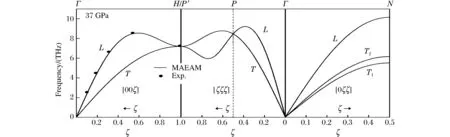
图5 压强p=37 GPa时钼的声子色散曲线 Fig.5 Phonon dispersion curves of W at 37 GPa

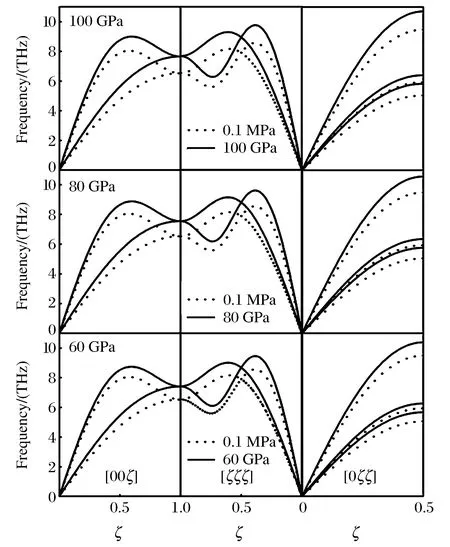
图6 不同高压下钼的声子色散曲线 Fig.6 Phonon dispersion curves of Mo under different high pressures

图6是压强分别为60、80和100 GPa时的声子色散曲线，其中固体实线是高压下的色散曲线，为了方便比较，在图6中我们还添加了常压下的色散曲线，并用点线表示。从图6中可以看出，常压下以及高压下(p=60、80和100 GPa)的声子色散曲线非常相似，这种相似性并不惊奇，因为金属钼保持体心立方结构直到我们所考虑的最大压强范围内(100 GPa)。高压下所有振动支的振动频率均高于常压下的振动频率，与常压声子色散相比，p=60 GPa时的最大振动频率增加了14.3%，p=80 GPa时增加了16.3%，p=100 GPa时增加了18.1%。在所有的振动支中的振动频率均随压强的增大而增大。在不考虑质量、相互作用距离和结合能所引起的差别时，这些现象和高压下体心立方金属钨[28]和钽[29]的计算结果相一致。

为了近一步说明声子频率和压强之间的关系，模拟了金属钼的T2[0ζζ]和L[00ζ]振动支中简约波矢分别为0.2、0.5、0.8 和1.0时的声子色散频率随压强的关系，如图7所示。从图7可以看出，在两个振动支上，4个简约点的声子频率均随压强的增加而增加。在相同振动支中各简约点的声子频率和压强之间的关系基本相同。因此，如果想知道声子色散和压强之间的关系时，我们只要考虑某一振动方向上某一简约点的振动情况即可。此外，在40～100 GPa范围内，各个简约点的频率和压强基本上呈线性关系。

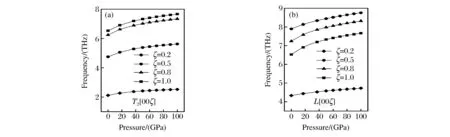
图7 不同简约波矢的声子频率和压强之间的关系 Fig.7 Phonon frequencies versus pressures at different reduced wave vectors

5 结 论

应用改进分析型嵌入原子法模型计算了不同高压下金属钼的原子力常数和动力学矩阵，重现了3种压强下金属钼沿3个高对称方向上声子色散的实验结果，预测了钼在压强分别为60、80和100 GPa时的声子色散曲线。得到以下结果：(1) 压强分别为0.1 MPa、17 GPa和37 GPa时金属钼的声子色散曲线的模拟结果和实验值符合较好，特别在低频附近二者几乎一致。(2) 在压强分别为p=60、80和100 GPa时所预测的声子色散曲线和常压下声子色散曲线的形状都非常相似，且随着压强的增大各振动支的振动频率均依次增大。(3) 不同振动支上不同简约点的声子频率均随压强的增加而增加，在40～100 GPa范围内，所考虑的各个简约点的频率和压强基本上呈线性关系。(4) 上述方法也可用于其他金属或合金在高压条件下声子色散关系的计算和研究。

[1] XIE Y,ZHANG J M.Atomistic simulation of phonon dispersion for body-centred cubic alkali metals [J].Can J Phys,2008,86(6):801-805.

[2] WANG Y,HECTOR L G,ZHANG H,et al.Thermodynamics of the Ceγ-αtransition:Density functional study [J].Phys Rev B,2008,78(10):104113.

[3] WONG J,KRISCH M,FARBER D L,et al.Crystal dynamics of fcc Pu-Ga alloy by high-resolution inelastic X-ray scattering [J].Phys Rev B,2005,72(6):064115.

[4] ADITYA M V.Phonon dispersion in equiatomic Li-based binary alloys [J].Chin Phys Lett,2008,25(2):654-657.

[5] DANIEL L F,KRISCH M,ANTONANGELI D,et al.Lattice dynamics of molybdenum at high pressure [J].Phys Rev Lett,2006,96(4):115502.

[6] MITTAL R,CHAPLOT S L,CHOUDHURY N,et al.Inelastic neutron scattering,lattice dynamics and high-pressure phase stability in LuPO4and YbPO4[J].J Phys-Condens Mat,2007,19(44):6202.

[7] FANG H,LIU B,GU M.High-pressure lattice dynamic and thermodynamic properties of Ir by first-principles calculation [J].Physica B,2010,405(2):732-737.

[8] HU C E,ZENG Z Y,ZHANG L.Theoretical investigation of the high pressure structure,lattice dynamics,phase transition,and thermal equation of state of titanium metal [J].J Appl Phys,2010,107(9):093509.

[9] KAZANC S.The effects on the lattice dynamical properties of the temperature and pressure in random NiPd alloy [J].Can J Phys,2013,91(10):833-838.

[10] ZHANG X J,CHEN C L,FENG F L.High-pressure phonon dispersion of copper by using the modified analytic embedded atom method [J].Chin Phys B,2013,22(9):096301.

[11] MORSE P M.Diatomic molecules according to the wave mechanics.Ⅱ.Vibrational levels [J].Phys Rev,1929,34(1):57-64.

[12] MURRELL J N,SORBIE K S.New analytic form for potential energy curves of stable diatomic states [J].J Chem Soc Faraday Trans,1974,70(2):1552-1556.

[13] SEBETCI A.A density functional study of bare and hydrogenated platinum clusters [J].Chem Phys,2006,331(1):9-18.

[14] DAW M S,BASKES M I.Embedded atom method:A review derivation and application to impurities,surface and other defects in metals [J].Phys Rev B,1984,29(12):6443-6447.

[15] BOYKIN T B,VOGL P.Dielectric response of molecules in empirical tight-binding theory [J].Phys Rev B,2002,65(3):035202.

[16] OUYANG Y F,ZHANG B W.Analytic embedded atom potentials for bcc metals:application to calculating the thermodynamic data of bcc alloys [J].Phys Lett A,1994,192(1):79-86.

[17] HU W Y,SHU X L,ZHANG B W.Point-defect properties in body-centered cubic transition metals with analytic EAM interatomic potentials [J].Comput Mater Sci,2002,23(1):175-189.

[18] MA F,ZHANG J M,XU K W.Theoretical analysis of interface energy for unrelaxed Ag (001)/Ni (001) twist interface boundaries with MAEAM [J].Surf Interface Anal,2004,36(4):355-359.

[19] ZHANG J M,WEI X M,XIN H,et al.Atomic scale calculation of energies of Cu (001) twist boundaries [J].Chin Phys,2004,14(5):1015-1020.

[20] DOVE M T.Introducton to lattice dynamics [M].New York:Cambridge University Press,1993.

[21] KAZANC S,OZGEN S.Pressure effect on phonon frequencies in some transition metals:A molecular dynamics study [J].Physica B,2005,365(1/2/3/4):185-192.

[22] KAZANC S,OZGEN S,ADIGUZEL O.Pressure effects on martensitic transformation under quenching process in a molecular dynamics model of NiAl alloy [J].Physica B,2003,334(3/4):375-381.

[23] ROSE J H,SMITH J R,GUINEA F,et al.Universal features of the equation of state of metals [J].Phys Rev B,1984,29(6):2963-2969.

[24] VINET P,ROSE J H,FERRANTE J,et al.Universal features of the equation of state of solids [J].J Phys-Condens Mat,1989,1(11):1941-1963.

[25] MAO H K,BELL P M,SHANER J W,et al.Specific volume measurements of Cu,Mo,Pd,and Ag and calibration of the rubyR1fluorescence pressure gauge from 0.06 to 1 Mbar [J].J Appl Phys,1978,49(6):3276-3283.

[26] WOODS A D B,CHEN S H.Lattice dynamics of molybdenum [J].Solid State Commun,1964,2(8):233-242.

[27] FARBER D L,KRISCH M,ANTONANGELI D,et al.Lattice dynamics of molybdenum at high pressure [J].Phys Rev Lett,2006,96(11):115502.

[28] ZHANG X J,CHEN C L.Pressure dependence of phonon dispersion in bcc tungsten [J].Chin J Phys,2013,51(2):359-367.

[29] TAIOLI S,CAZORLA C,GILLAN M J,et al.Melting curve of tantalum from first principles [J].Phys Rev B,2007,75(21):214103.