二维骨料随机分布混凝土的动态力学性能数值模拟*

刘海峰,韩 莉

(宁夏大学土木与水利工程学院,宁夏银川 750021)

1 引 言

混凝土是以硬化水泥砂浆为基体和粗骨料为填充材料组成的非均匀复合材料。凭借其原材料就地取材方便、成本较低等优势，广泛应用于各种民用建筑及军事设施。这些混凝土结构在其工作过程中除了承受正常的准静态载荷外，往往还要承受各种急剧变化的冲击、碰撞等动荷载。混凝土受到冲击荷载作用时，表现出与静态荷载作用下不同的力学性能，为了更好地设计和分析这些混凝土结构，必须对其动态力学性能做进一步的研究。

混凝土在冲击过程中应力和变形的变化常常以波的形式传播，具有强烈的瞬态行为，而试验中很难观察到其细观破坏过程。通过数值模拟，冲击过程中的变形、应力变化可以直观地展示出来，为试验提供一定的理论指导，降低试验成本。

混凝土中粗骨料的大小及分布对混凝土的动态力学性能有很大影响。目前，国内外学者在这方面进行了许多研究。Park等[1]对高应变率下混凝土和水泥砂浆进行有限元模拟，分析了冲击荷载下混凝土和水泥砂浆的承载能力、能量吸收和微观结构。Pedersen等[2]利用骨料嵌入水泥砂浆基体的理想二维细观模型研究了加载速率对混凝土动态力学性能的影响。刘光廷、王宗敏等[3-4]根据混凝土的骨料级配曲线，借助于蒙特卡罗方法生成随机骨料，模拟了单边裂缝受拉试件断裂破坏的全过程。马怀发等[5]基于混凝土随机骨料结构，提出了既能反映骨料分布随机性，又能反映各相材料力学特性随机性的三维细观力学数值模型。杜修力等[6]采用材料特征单元尺度法来剖分有限元网格并投影到建立的随机骨料模型上，提出了随机多尺度力学模型分析方法。孔令超等[7]基于均匀化理论，假设粗骨料在混凝土中随机分布并利用C++语言编写随机分布颗粒生成程序，对混凝土在静动态压缩载荷作用下的力学响应情况及破坏形态进行了预测。宋来忠等[8]基于参数化骨料的特点，采用按级配分级随机投放的方式，保证了骨料分布的合理性，实现了满足大体积、全级配、高强度混凝土的骨料投放模拟要求。张柱等[9]利用轻气炮对混凝土材料进行了不同冲击速度下的动态力学性能实验，随后利用AUTODYN软件进行数值模拟，将模拟结果与实验结果进行比较，解释了飞片和靶板破坏过程中波的传播过程。但针对试件尺寸、粗骨料大小及分布和粗骨料体积分数对混凝土动态力学性能的影响目前研究较少。

根据富勒级配曲线和瓦拉文平面转化公式，利用ANSYS自带的APDL语言编写了混凝土二维圆形骨料随机分布程序，通过ANSYS/LS-DYNA软件对冲击速度、试件尺寸、粗骨料体积分数和粗骨料大小及分布不同的混凝土动态特性进行数值模拟，研究冲击速度、试件尺寸、粗骨料大小及分布和粗骨料体积分数对混凝土动态力学性能的影响规律，并讨论冲击荷载作用下混凝土的动态破坏模式。

2 骨料的随机投放

Fuller等[10]经过大量研究，提出了三维Fuller 骨料级配曲线，此曲线为最大密度理想级配曲线，认为级配曲线越接近抛物线时其密度越大。Fuller 骨料级配曲线用如下方程表示

(1)

式中：P为骨料通过直径为D的筛孔百分数，D和Dmax分别为筛孔的直径和骨料的最大粒径。

在概率统计学的基础上，Walraven等[11]给出了Fuller 曲线的平面转化公式，即瓦拉文平面转化公式

(2)

式中：PK为骨料体积与总体积的百分比，D0为骨料的最小直径,Dmax为骨料的最大直径。

利用(1)式和(2)式将粗骨料体积分数换算成面积分数，利用ANSYS自带的APDL语言编写了混凝土二维圆形骨料随机分布程序。

3 有限元分析

3.1 FE模型

采用ANSYS/LS-DYNA动力分析软件模拟了二维圆形骨料随机分布的混凝土在冲击荷载下的动力响应。有限元模型如图1所示，中间部分为混凝土试件，下面的刚性板起支撑作用，上面的刚性板相当于作动器，对上面的刚性板施加不同的速度来模拟不同冲击速度下的混凝土破坏。

线阵声学段内张力则关系到系固在段内的水听器的安全保障性能及其工作稳定性。因此，准确对线阵声学段内张力进行估计和预报是非常有必要的。

采用3种不同试件尺寸的模型，直径74 mm、高70 mm的圆柱体试件，边长为100 mm的立方体试件，边长为150 mm的立方体试件。数值模拟时粗骨料的最小粒径取为5 mm[12]。图1为粗骨料体积分数为20%，骨料粒径为5～10 mm的不同试件尺寸的有限元模型。网格划分时，水泥砂浆基体采用映射网格，圆形骨料采用自由网格划分。砂浆基体和骨料选用Plane162二维实体单元。

3.2 接触定义与边界条件

刚性板速度方向垂直于试件，刚性板与试件之间设有一定摩擦，为保证单元失效接触保持有效，采用二维单面自动接触*CONTACT_2D_AUTOMATIC_SINGLE_SURFACE。下方刚性板固支。

3.3 材料模型

数值模拟时水泥砂浆和粗骨料的本构模型均采用HJC模型[13]，该模型表示如下

(3)

损伤D由塑性应变累积而成，由(4)式确定

(4)

图2 HJC状态方程曲线 Fig.2 HJC curve of equation of state

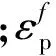
p为静水压力，由图2所示状态曲线确定。

OA阶段：弹性压缩区，p=Kμ，K为体积模量；

AB阶段：压实变形区，p=pc+K′μ，其中K′=(p1-pc)/(μp1-μc)；

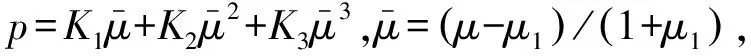
水泥砂浆和骨料引入MAT_ADD_EROSION侵蚀失效准则来控制单元失效。由于拉伸破坏和剪切破坏是混凝土破坏的两种常见方式，且多数情况下主要是拉伸破坏，剪切破坏占的比例很小，因此采用主应变失效方式，主应变取0.002[7]。刚性板采用MAT_RIGID模型。

3.4 材料参数选取

表1 砂浆模型参数 Table 1 Model parameters of cement mortar

表2 骨料模型参数 Table 2 Model parameters of coarse aggregate

数值模拟结果和冲击荷载作用下混凝土试验结果[15]比较如图3所示。混凝土冲击压缩试验是在直锥变截面式∅74 mm SHPB 实验装置上进行，试件尺寸为直径74 mm、高70 mm的圆柱体，数值模拟时模型尺寸、粗骨料的体积分数、粗骨料最小粒径和最大粒径与实验一致，作动器与混凝土之间设置了摩擦接触。实验的宏观破坏是典型的圆锥角形破坏，数值模拟中可以看出微裂纹沿着骨料薄弱界面成核、扩展，形成主干裂纹，近似成圆锥角形破坏。

(a) Experimental,impact velocity:15.67 m/s (b) Simulated,impact velocity:15.00 m/s 图3 混凝土破坏形式 Fig.3 Failure mode of concrete

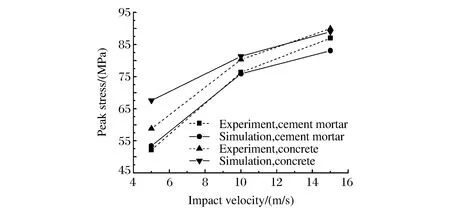
图4 实验与数值模拟峰值应力比较 Fig.4 Comparison of peak stress:experimental versus numerical simulation results

图4是实验与数值模拟峰值应力比较，水泥砂浆和混凝土在冲击速度为5、10、15 m/s时，数值模拟与实验得到的峰值应力相差分别为2.51%，14.95%，-0.5%，1.3%，-4.48%，-1.12%。由图3和图4可以看出，数值模拟结果与实验结果吻合较好。由此可见，本研究所建立的有限元模型及选取模型参数是可靠的，可以进一步进行混凝土动态力学性能的模拟。

4 数值模拟结果及分析

4.1 混凝土的冲击破坏模式

图5为粗骨料体积分数为30%、粗骨料粒径介于5～10 mm、尺寸为100 mm×100 mm×100 mm的试件在不同冲击速度下破坏过程的应力云图。冲击速度为5 m/s时，混凝土没有发生破坏，没有明显的裂纹，如图5(a)所示，这与实验结果[15]吻合。冲击速度为10 m/s时，冲击破坏过程如图5(b)所示，应力波在到达试件底部之前，在试件内通过冲击产生的能量不足以使单元发生破坏，而到了底部之后，一部分应力波反射回试件，这时底部除了由顶部冲击传播而来的动力响应，应力波的部分反射也加强了底部的应力应变场，致使裂纹先从底部出现，向上扩展，同时不断有新的微裂纹成核、扩展，这些裂纹相互贯通使试件破坏。当冲击速度增加到15 m/s时，如图5(c)所示，这时在试件内通过冲击产生的能量足以使部分单元发生破坏，所以在应力波自上而下的传播过程中，就伴随单元破坏，因此冲击速度越高，初始时在冲击端累积的应力应变场越强。

图5 混凝土的冲击破坏过程 Fig.5 Impact failure process of concrete

在整个破坏过程中，混凝土试件大体呈现锥型破坏，试件两端部与中间相比单元破坏较少，这是由于端部摩擦力的存在一定程度上约束混凝土的横向变形。

在低速加载下，裂纹数比较少，破坏时呈现出集中主干式的宏观主裂纹，迅速扩展，贯通直至试件完全破坏。随着冲击速度的增加，裂纹数逐渐增多，更多的裂纹迅速扩展、贯通，形成多条宏观裂纹，导致试件破坏。

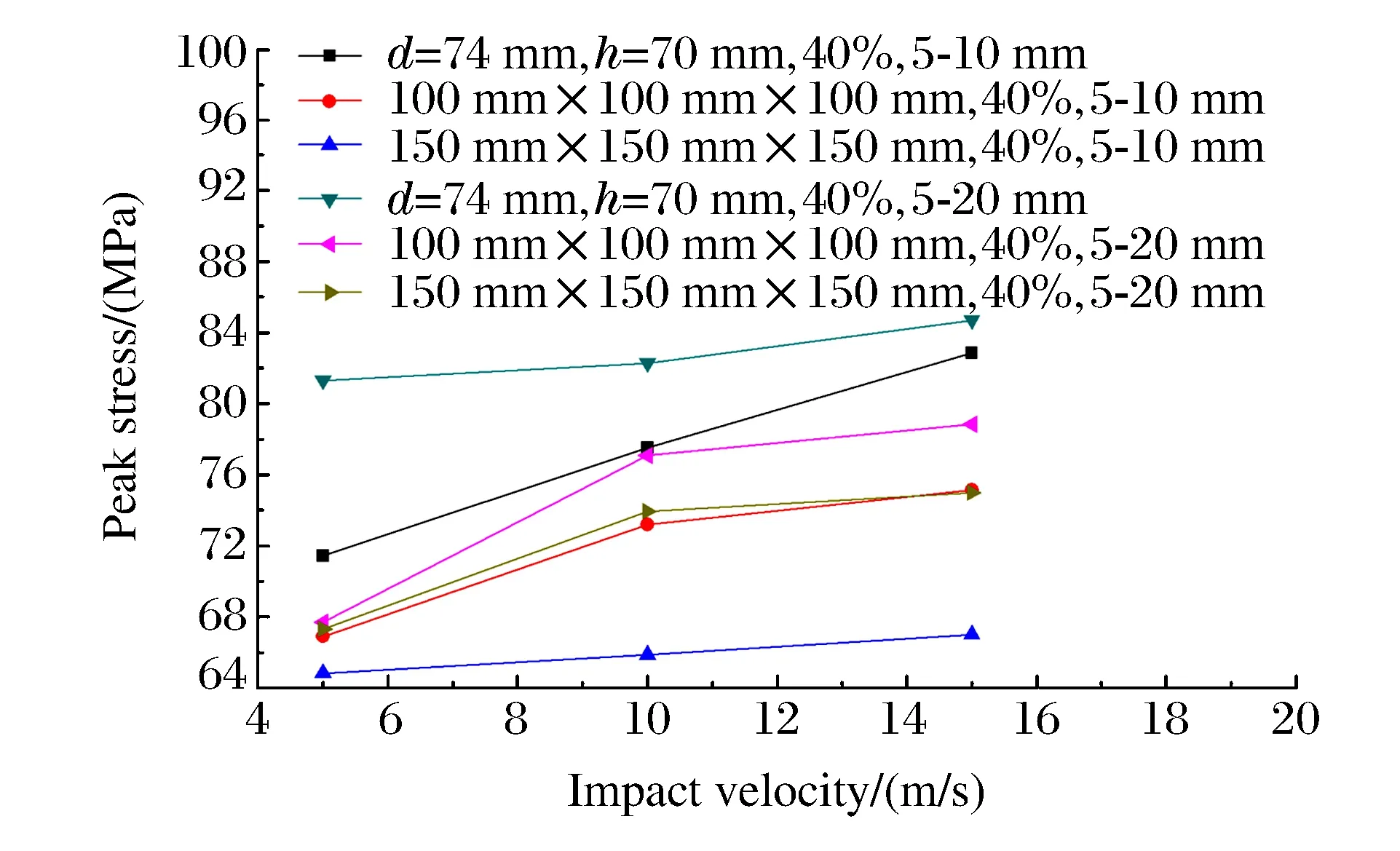
图6 混凝土峰值应力与冲击速度的关系 Fig.6 Peak stress of concrete versus impact speed

4.2 冲击速度的影响

对粗骨料体积分数为40%，粒径分别为5～10 mm、5～20 mm，试件尺寸为直径74 mm、高70 mm，100 mm×100 mm×100 mm，150 mm×150 mm×150 mm的3种混凝土试件在不同冲击速度下的破坏进行模拟，分析了冲击速度对其峰值应力的影响，如图6所示。

图6表明，随着冲击速度的增加，混凝土峰值应力呈现逐渐增加的趋势，因此混凝土是一种率敏感性材料。在较低冲击速度下，冲击产生的能量较小，发生成核、扩展的裂纹数较少，裂纹具有足够的时间扩展，裂纹之间的相互作用较少，因此应力水平较低，峰值应力较小；在较高冲击速度下，冲击产生的能量较大，没有足够的时间供稳态裂纹的扩展、合并，导致众多的微裂纹几乎同时扩展并且相互作用，因而表现出材料能够承受较高的应力，峰值应力相应较大[16]。

4.3 试件尺寸的影响

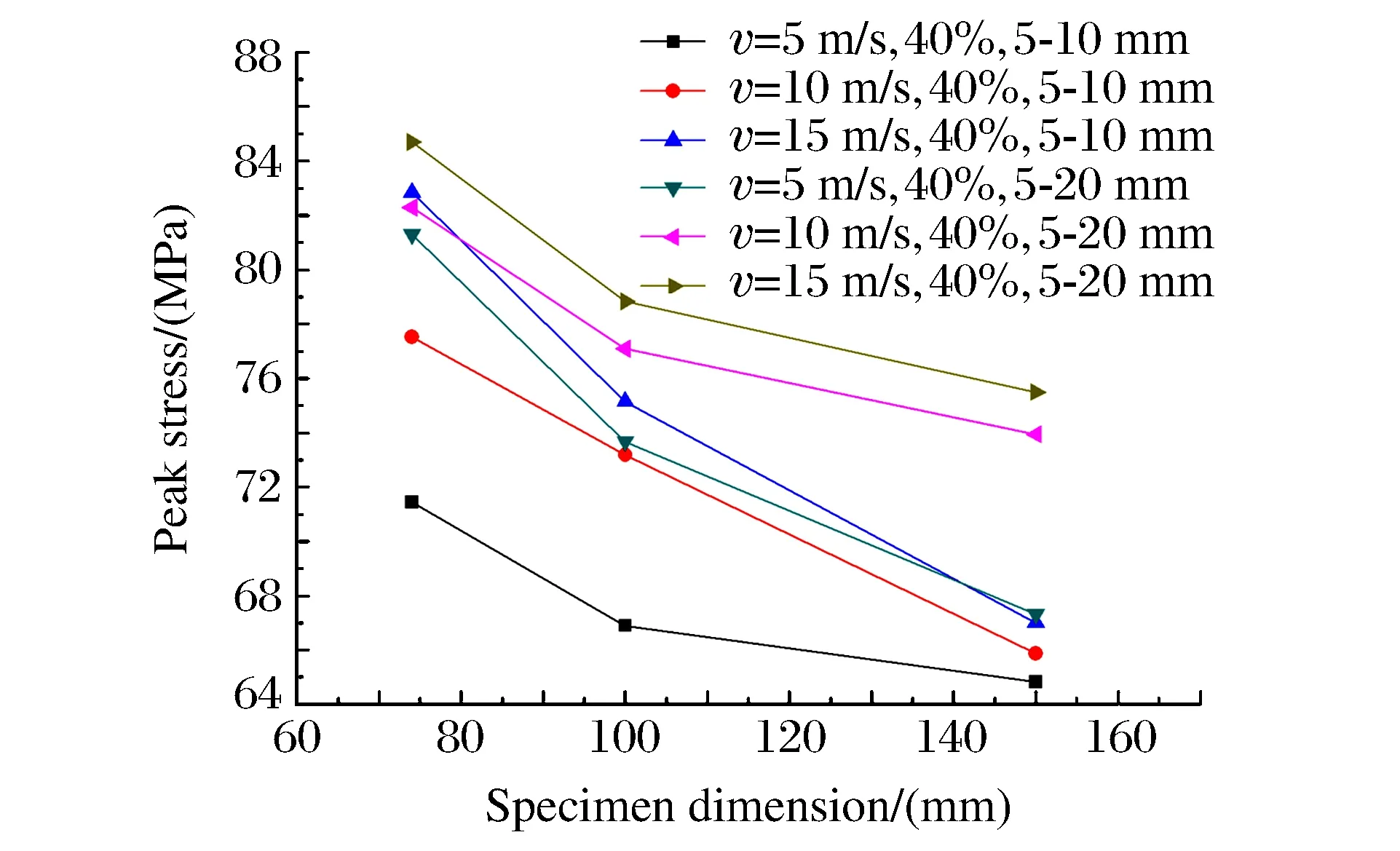
图7 混凝土峰值应力与试件尺寸关系 Fig.7 Peak stress of concrete versus specimen dimension

图7为粗骨料体积分数为40%，粒径分别为5～10 mm、5～20 mm时，混凝土试件尺寸对峰值应力的影响。由图7可知，随着试件尺寸的增加，混凝土峰值应力呈现逐渐减小的趋势，表现出明显的尺寸效应。

4.4 粗骨料粒径的影响

以直径74 mm、高70 mm，100 mm×100 mm×100 mm,150 mm×150 mm×150 mm混凝土试件为研究对象，考察冲击速度为10 m/s时，混凝土粗骨料最小粒径和最大粒径对混凝土峰值应力的影响。

保持粗骨料最大粒径25 mm不变，不断改变粗骨料最小粒径，分析粗骨料最小粒径对冲击荷载下混凝土峰值应力的影响，如图8所示。从图8中可以看出，随着粗骨料最小粒径的增大，混凝土的峰值应力逐渐减小，粗骨料最小粒径为5 mm时混凝土峰值应力最大。

图8 混凝土粗骨料最小粒径对峰值应力影响 Fig.8 Influence of minimum diameter of coarse aggregate on the peak stress of concrete

保持粗骨料最小粒径5 mm不变，不断改变粗骨料最大粒径，分析粗骨料最大粒径对混凝土峰值应力的影响，如图9所示。从图9可以看出，随着粗骨料最大粒径的增大，冲击荷载作用下混凝土的峰值应力呈现先增大后减小的趋势，粗骨料最大粒径为20 mm时混凝土峰值应力最大。

图9 混凝土粗骨料最大粒径对峰值应力影响 Fig.9 Influence of maximum diameter of coarse aggregate on the peak stress of concrete

这是由于粗骨料粒径越大，表面积越大，其比表面积就会越小，即同样体积分数的粗骨料需要的水泥用量减少，因此粗骨料最大粒径在某一临界值内越大越好，一旦超过该临界值，在粗骨料体积分数保持不变的前提下，随着粗骨料最大粒径增大，混凝土内部的均匀性越差，从而降低混凝土硬化后的整体强度。由此可以看出，粗骨料粒径级配直接影响混凝土的强度，较好的骨料级配应当是：粗大骨料颗粒形成的孔隙被中等粒径的砂粒所填充，而中等骨料颗粒形成的孔隙被较小粒径的砂粒所填充，使孔隙率变小，从而提高混凝土强度和工作性能。

4.5 体积分数的影响

以直径74 mm、高70 mm，100 mm×100 mm×100 mm、150 mm×150 mm×150 mm 3种尺寸的混凝土试件为研究对象，考察冲击速度为10 m/s时，混凝土粗骨料体积分数对混凝土峰值应力的影响，如图10所示。从图10可以看出，随着粗骨料体积分数的增加，混凝土的峰值应力呈现先增大后减小的趋势，当粗骨料体积分数为40%时混凝土峰值应力最大。这是因为当粗骨料体积分数小于40%时，粗骨料较少，水泥砂浆较多，而水泥砂浆的强度远小于粗骨料的强度，所以混凝土的强度偏低。当粗骨料体积分数大于40%时，在水灰比一定的情况下，粗骨料较多，水泥砂浆较少，无法牢固粘接粗骨料，而且薄弱界面较多，所以混凝土强度降低。

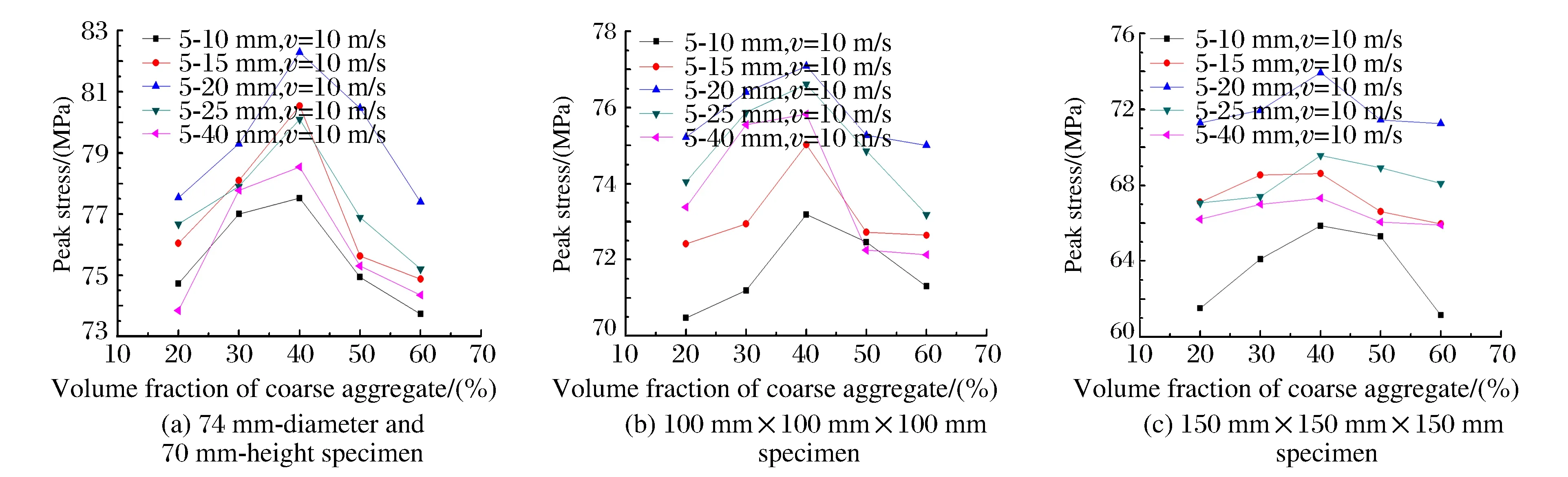
图10 混凝土粗骨料体积分数对峰值应力的影响 Fig.10 Influence of volume fraction of coarse aggregate on the peak stress of concrete

5 结 论

混凝土材料冲击特性响应是一个非常复杂的过程，不仅涉及了材料内部微结构损伤缺陷(微裂纹和微空洞等)的演化发展，而且还涉及了材料应变率敏感效应和静水压力相关性的影响。粗骨料的大小及分布对混凝土的动态力学性能有很大影响。将混凝土看成粗骨料和水泥砂浆组成的二相非均质复合材料，根据富勒级配曲线和瓦拉文平面转化公式，利用ANSYS自带的APDL语言编写了混凝土二维圆形骨料随机分布程序，应用刚性板冲击加载的方式研究了混凝土的动力响应，分析冲击速度、试件尺寸、粗骨料大小及分布和粗骨料体积分数对混凝土动态力学性能的影响，讨论了混凝土的冲击破坏模式。数值模拟表明：混凝土的峰值应力随着冲击速度的增大而增大，具有明显的率效应；混凝土的峰值应力随着模型尺寸的增大而减小，表现出明显的尺寸效应；随着粗骨料体积分数增大，冲击荷载作用下混凝土的峰值应力呈现先增大后减小的趋势，粗骨料体积分数为40%时混凝土峰值应力最大；保持粗骨料最大粒径不变，随着粗骨料最小粒径的增大，混凝土的峰值应力逐渐较小；保持粗骨料最小粒径5 mm不变，随着粗骨料最大粒径的增大，混凝土的峰值应力呈现先增大后减小的趋势。为了进一步提高数值模拟的可靠性和精度，在数值模拟时，今后还需要考虑粗骨料和水泥砂浆基体之间界面相对混凝土动态力学性能的影响，为混凝土的工程应用提供理论依据和技术支撑。

[1] PARK S W,XIA Q,ZHOU M.Dynamic behavior of concrete at high strain rates and pressures:Ⅱ.Numerical simulation [J].Int J Impact Eng,2001,25(9):887-910.

[2] PEDERSEN R R,SIMONE A,SLUYS L J.Mesoscopic modeling and simulation of the dynamic tensile behavior of concrete [J].Cement Concrete Res,2013,50(1):74-87.

[3] 刘光廷,王宗敏.用随机骨料模型数值模拟混凝土材料的断裂 [J].清华大学学报,1996,36(1):84-89.

LIU G T,WANG Z M.Numerical simulation study of fracture of concrete materials using random aggregate model [J].Journal of Tsinghua University (Sci & Tech),1996,36(1):84-89.

[4] 王宗敏,邱志章.混凝土细观随机骨料结构与有限元网格剖分 [J].计算力学学报,2005,22(6):728-732.

WANG Z M,QIU Z Z.Random aggregate structure of mesoscopic concrete and finite element mesh [J].Chinese Journal of Computational Mechanics,2005,22(6):728-732.

[5] 马怀发,陈厚群,吴建平,等.大坝凝土三维细观力学数值模型研究 [J].计算力学学报,2008,25(2):241-247.

MA H F,CHEN H Q,WU J P,et al.Study on numerical simulation of 3D meso-mechanics model of dam concrete [J].Chinese Journal of Computational Mechanics,2008,25(2):241-247.

[6] 杜修力,金 浏.基于随机多尺度力学模型的混凝土力学特性研究 [J].工程力学,2011,28(增刊Ⅰ):151-155.

DU X L,JIN L.Mechanical property research on concrete based on random multi-scale mechanical model [J].Engineering Mechanics,2011,28(Suppl Ⅰ):151-155.

[7] 孔令超.用均匀化方法研究研究细观粒状材料的力学性能 [D].北京:北京理工大学,2008.

KONG L C.Research on the mechanical behavior of micro-granular material by means of homogenization theory [D].Beijing:Beijing Institute of Technology,2008.

[8] 宋来忠,沈 涛,余 波.混凝土二维参数化骨料模型的创建方法 [J].工程力学,2013,30(10):5-13.

SONG L Z,SHEN T,YU B.The approach to establishing a two-dimensional parameterized aggregate model for concrete simulation [J].Engineering Mechanics,2013,30(10):5-13.

[9] 张 柱,赵 慧,于 晖.混凝土材料动态力学性能实验与数值模拟研究 [J].高压物理学报,2011,25(6):533-538.

ZHANG Z,ZHAO H,YU H.Experiments and numerical simulations of concrete dynamic mechanical properties [J].Chinese Journal of High Pressure Physics,2011,25(6):533-538.

[10] FULLER W B,THOMPSON S E.The laws of proportioning concrete [J].J Transport Div,1907,59(1):67-14.

[11] WALARAVEN J C,REINHARDT H W.Theory and experiments on the mechanical behavior of cracks in plain and reinforced concrete subjected to shear loading [J].Heron,1981,26(1A):26-35.

[12] 陈志源,李启令.土木工程材料 [M].第2版.武汉:武汉理工大学出版社,2009.

CHEN Z Y,LI Q L.Civil engineering materials [M].2nd ed.Wuhan:Wuhan University of Technology Press,2009.

[13] HOLMQUIST T J,JOHNSON G R,COOK W H.A computational constitutive model for concrete subjective to large strains,high strain rates and high pressures [C]//JACKSON N,DICKERS S.The 14th international symposium on Ballistics.Québec,Canada,1993.

[14] 曾 毅.基于细观力学的碎石混凝土侵彻数值模拟 [D].绵阳:西南科技大学,2012.

ZENG Y.Numerical simulation of penetration of macadam concrete based on mesomechanics [D].Mianyang:Southwest University of Science and Technology,2012.

[15] LIU H F,NING J G.Constitutive model for concrete subjected to impact loading [J].Journal of Southeast University (English Edition),2012,28(1):79-84.

[16] LIU H F,LIU H Y,SONG W D.Fracture characteristics of concrete subjected to impact loading [J].Science China:Physics,Mechanics & Astronomy,2010,53(2):253-26.