直接空冷凝汽器翅片管积灰的换热特性研究
2016-04-25张学镭孙苗青葛永建段俊阳
张学镭,孙苗青,葛永建,段俊阳
(华北电力大学 能源动力与机械工程学院,河北保定071003)
直接空冷凝汽器翅片管积灰的换热特性研究
张学镭,孙苗青,葛永建,段俊阳
(华北电力大学 能源动力与机械工程学院,河北保定071003)
为了深入研究空冷凝汽器散热管束积灰时的传热与流动特性,利用FLUENT软件数值模拟了翅片管束不同积灰厚度的传热及流动情况,对比分析了翅片管束不同积灰厚度的压力分布、温度分布及速度分布,计算得到了翅片管束5种积灰厚度的对流换热系数、传热系数及流动阻力随迎面风速变化的规律,拟合得到了摩擦系数及努塞尔数随雷诺数变化的关系。结果表明:随着迎面风速的增加,积灰前后的管外对流换热系数、传热系数以及流动阻力逐渐增加;同一迎面风速下,随积灰厚度的增加,对流换热系数和流动阻力增大,传热系数减小。
蛇形翅片扁平管;迎面风速;积灰厚度;流动换热特性
0 引言
西北富煤缺水地区所建的火电机组广泛应用了直接空冷系统,直接空冷凝汽器性能的优劣是决定机组能否安全、经济、有效运行的重要因素之一[1,2]。在西北地区,直接空冷机组的装机容量在不断扩大,空冷凝汽器长期置于室外运行,散热管束结构紧密,管束之间空气流道狭窄,且该地长年风沙天气较多,极易产生积灰,空冷凝汽器积灰现象也比较严重[3]。积灰严重影响翅片管外空气的传热与流动特性,导致空冷凝汽器换热性能恶化。因此研究直接空冷凝汽器散热管束的积灰特性,对于保证机组的安全高效运行具有十分重要的意义。
国内关于空冷凝汽器散热管束积灰方面的研究,文献[3]等运用传热学知识及换热器理论计算推导散热管束的传热系数随不同积灰厚度之间的变化关系,得出机组出力随翅片管外积灰厚度的变化规律,以300 MW机组为例,当积灰厚度为1 mm时,机组的出力减少1.4%。文献[4-6]等针对直接空冷凝汽器单元在翅片管外积灰影响下换热情况的不同,提出了运用温度监测的方法来调节积灰单元的风机转速,并运用理论知识计算验证了该调节方式的经济性。文献[7]等以两翅片间的单一流道为研究对象,在设定风机功率不变且不考虑积灰自身热阻的条件下进行研究,得出:翅片积灰后,散热管束换热量随污垢层的变厚而迅速下降,空冷凝汽器换热负荷下降,空气的温升增大。文献[8]等分析了积灰和迎面风速两种情况对传热系数和机组背压的影响规律,得出:积灰和迎面风速的降低,都会使机组的换热能力下降;随着积灰厚度的增加,机组背压就越高,且迎面风速降低,机组背压上升。文献[9]等运用FLUENT软件对空冷凝汽器U型管束进行数值模拟,得到空气对流换热、平均努赛尔数和摩擦系数随雷诺数的变化规律,且拟合得出相应的关系式。
目前,针对直接空冷凝汽器翅片管积灰特性的数值模拟研究较少,本文以典型600 MW 直接空冷凝汽器蛇形翅片单排管为研究对象,建立了单排管翅片积灰前后的数值分析模型,重点分析在不同的迎面风速下,空冷凝汽器单排管翅片积灰前后的传热与流动特性。
1 数学模型
实际的散热器翅片结构如图1所示,其结构参数如表1。翅片是焊接在扁管上的,扁管的厚度为0.25 mm。考虑到翅片结构的对称性,所取的计算域是一个对称性区域,翅片结构呈Z字形。

图1 蛇形翅片单排扁管结构示意图

mm
为了避免计算区域入口处的入口效应和出口边界的回流现象对计算结果产生影响,入口、出口区域适当延长,分别为50 mm、240 mm。用GAMBIT软件对其建立物理建模,计算区域分为入口区、翅片区、基管区和出口区四部分,并对这四部分区域划分网格。
为了便于计算,扁平管蛇形翅片散热器数学模型作如下简化假设[10,11]:
(1)环境温度为常数,取空气进口温度为305 K;
(2)翅片材料和基管导热系数为常数;
(3)计算域中的换热与流动是稳态的;
(4)忽略基管与翅片的辐射换热;
(5)计算域中的空气可认为不可压缩流体。
1.1 控制方程
在稳态、不可压缩以及常物性条件下,翅片管流动换热控制方程如下[12]:
连续方程:
(1)
动量方程:
(2)
能量方程:
(3)
湍动能方程:
(4)
湍流动能耗散率方程:
(5)
式中:ρ为空气密度,kg/m3;ui为i方向的速度(i=1,2,3分别表示x,y,z),m/s;P为压力,Pa;Τ为温度,K;k为湍动能;ε为湍动能耗散率;μeff为有效粘性系数,kg/(m·s);μi为湍流粘性系数, kg/(m·s);μ为空气动力粘度系数,kg/(m·s);Gk为由平均速度梯度引起的湍动能的产生项;C1ε,C2ε,C3ε,σk,σt和σε为经验常数[12]。
1.2 边界条件
(1)入口设为速度入口边界,湍流强度设为10%,空气入口温度为305 K;出口设为压力出口边界;空气侧的对称平面均设为对称性边界;
(2)积灰前后的基管内壁温设为相同,基管内壁设为定壁温边界,温度设为342 K;
(3)基管内外壁和翅片表面设为固体壁温条件;基管和翅片的对称平面均设为对称性边界;
(4)基管材料为碳钢,翅片材料为铝;
(5)采用分块划分网格的方法,将模型分割为多个几何体。每个几何体统一采用六面体网格,入口、出口及基管区域采用相对稀疏的网格,翅片区域采用相对密集的网格。为了确定网格的数目,针对55万、76万以及120万的网格进行计算比较,结果差距小于1%,验证了网格数目对计算结果的无关性,最后确定积灰前的网格数目为76万左右,积灰后的网格数目为87万左右。
1.3 收敛准则
采用FLUENT默认的收敛准则:Energy方程的计算残差低于10-6,其他各方程的计算残差都低于10-3。
1.4 计算方法
数值模拟采用有限体积法,分离求解器用隐式求解,压力与速度耦合采用Simple算法,能量方程的离散采用一阶Upwind。
针对翅片管外均匀积灰进行数值模拟时,考虑翅片上表面积灰和扁平管积灰,建立积灰模型与建立清洁模型的步骤相同,据此对翅片管外积灰厚度为0 mm、0.1 mm、0.2 mm、0.3 mm、0.4 mm的物理模型进行模拟。
1.5 数据处理
(1)管外气侧对流换热系数h0
换热过程中,翅片和基管对空气的换热量表示为[4]:
(6)
空气流经翅片区域带走的热量可表示为:
(7)
管外气侧平均对流换热系数为:
(8)
翅片效率为[5]:
(9)
其中:
(10)
式中:Q为换热量,W;m为空气质量流量,kg·s-1;Cp为空气定压比热,kJ/(kg·K);A为翅片管气侧换热面积,m2;Af为翅片表面积,m2;At为基管表面积,m2;tw为基管外壁温度,℃;tin为来流空气温度,℃;tout为空气流经翅片管的出口温度,℃;ηf为翅片效率;λt为翅片管导热系数,W/(m·K);δt翅片管壁厚度。
对流换热系数的具体计算流程如图2。
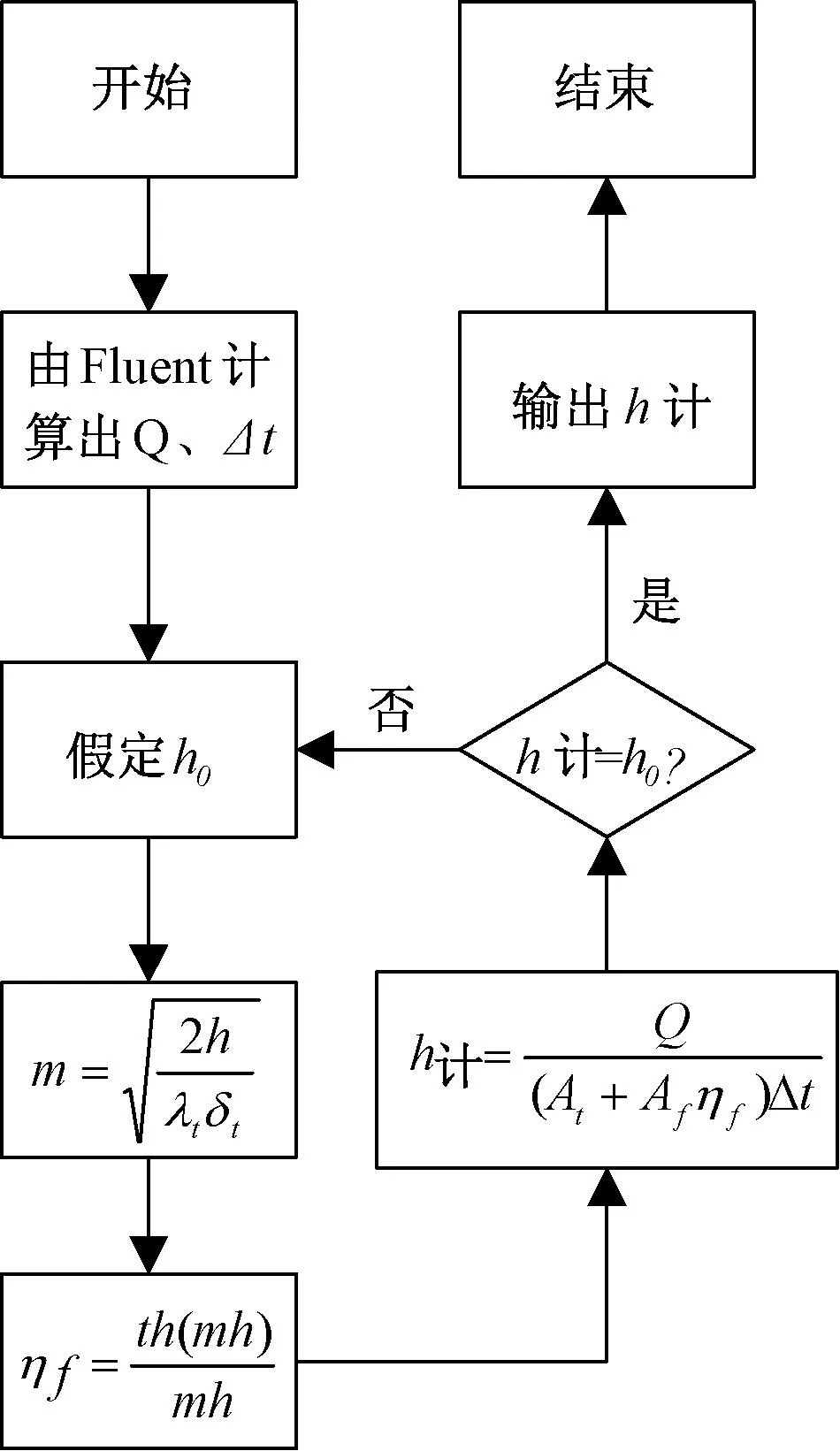
图2 对流换热系数的计算流程图
(2)管内蒸汽凝结换热系数hi
管内蒸汽凝结换热系数为[5]:
(11)
式中:g为重力系数;ρ为蒸汽密度,kg/m3;λw为蒸汽导热系数,W/(m·K);r为蒸汽汽化潜热,kJ/kg;η为蒸汽动力粘度,Pa·s;l为特征长度,m;ts,tw分别为蒸汽温度和壁面温度,K。
(3)传热系数K
以空气侧翅片管总面积为基准的传热系数表达式为[5]:
(12)
式中:肋化系数β为:
(13)
肋壁总效率η0为:
(14)
翅片管空气侧总传热面积A0为:
A0=At+Af
(15)
假设翅片管基管外表面和翅片上表面积灰均匀,积灰厚度为δd,以翅片间流道总传热面积为基准的传热系数K[6]为:
(16)
式中:K0为积灰前的传热系数,W/(m2·K);λ为管壁材料导热系数,W/(m·K);δ为管壁厚度,mm;Ai为蒸汽侧传热面积;K为积灰后的传热系数,W/(m2·K);h0’为积灰后管外空气对流换热系数,W/(m2·K);c为考虑到翅片仅在上表面而引入的积灰系数,取0.4[6];λd为积灰的导热系数,取0.4W/(m·K)[6]。
(4)空气流经翅片管的流动阻力
(17)
式中:Pin为进口平均压力,Pa;Pout为出口平均压力,Pa。
(5) 雷诺数[5]
(18)
式中:当量直径de[2]为:
(19)
u为翅片间最小流通截面上的流速,m·s-1;v为空气的运动粘度,m2/s;P为翅片的间距,mm;h为翅片的高度,mm。
(6) 摩擦系数
(20)
式中:u为来流速度,m·s-1;ρ为来流密度,kg/m3。
(7) 努塞尔数[5]
(21)
式中:λ为空气的导热系数,W/(m·K)。
2 翅片空间空气的流场分布
本文针对积灰0 mm、积灰0.1 mm、积灰0.2 mm、积灰0.3 mm、积灰0.4 mm 5种工况,对每种工况数值模拟5种迎面风速 1m/s,1.5 m/s, 2 m/s,2.5 m/s,3 m/s,分析翅片空间的流动、换热特性。由于模拟结果呈现的规律性相差不大,因此仅对迎面风速2 m/s下,积灰0 mm和积灰0.3 mm两种工况,分析翅片空间的压力场、速度场、温度场。
2.1 压力场
压力分布如图3,图4所示。空气流经翅片区域时,由于翅片区域流动阻力的存在,压力呈逐渐减小的趋势,进口处压力最大,由于计算域出口设置的是压力出口边界,出口处压力最小,值为0 Pa。
积灰后的入口压力比积灰前的入口压力要大。在同一风速下,积灰前后通过的体积流量是一定的,积灰后流道变窄,在入口区,形成一定的集聚,导致入口压力比积灰前要大。

图3 积灰0mm时的压力场
图4 积灰0.3mm时的压力场
2.2 温度场
温度分布如图5,图6所示。冷却空气由入口端流经翅片区域的过程中,冷却空气不断带走翅片管及基管外表面的热量,空气温度逐渐升高,在空气流经翅片出口时温度达到最大值。翅片的尾涡区温度较高,是因为扁管背风侧尾部区域速度很小且存在回流现象,致使热量不能及时被带走,加热过的热空气又重新回到基管被加热,导致尾涡区温度升高,空气冷却效果明显减弱。
积灰后的温度分布与积灰前相比,不同的是翅片管的后半部分高温区域面积变大。这说明了翅片积灰后,空气流经翅片的过程中温度升高很快,空气与翅片管间的温差减小,导致翅片管的后半部分换热能力下降。

图5 积灰0 mm时的温度场
图6 积灰0.3 mm时的温度场
2.3 速度场
速度分布如图7,图8所示。空气流经翅片时,流速呈先上升后下降的趋势。空气由入口区进入翅片区域时,流通截面积减小,速度增大,在翅片区域,流通截面积几乎不变,风速保持不变。空气由翅片区进入出口区时,流通截面积增大,速度又有所减小。翅片区域几何结构的差异与冷却空气的流速有密切的关系。
空气流过翅片区域时,积灰后的速度比积灰前的速度要大。这是由于计算域的进口设置的是速度入口边界,通流量是恒定的,但由于积灰后通流面积减少,所以积灰后流速会略微增加。

图7 积灰0mm时的速度场
图8 积灰0.3mm时的速度场
3 迎面风速对翅片积灰前后的换热流动的影响
针对空冷凝汽器翅片管积灰前后5种工况,即积灰0~0.4 mm,进行数值模拟。选取迎面风速1~3 m/s 5种情况,分析翅片空间的流动、换热特性。模拟结果显示,当翅片管积灰后,对流换热系数、传热系数、空气流经翅片管的阻力以及摩擦系数均发生变化。
3.1 结果及分析
不同迎面风速下,积灰0~0.4 mm时5种工况下的凝汽器翅片管外气侧对流换热系数h0、传热系数K、进出口的压力降ΔP分别见图9,图10和图11。
从图9可以看出,随着迎面风速的增加,积灰前后5种工况下的翅片管外对流换热系数呈逐渐增大的趋势,由于风速增加,翅片内空气流动受到的扰动就越大,空气侧对流换热效果得到增强;在同一迎面风速下,积灰后的管外对流换热系数与积灰前相比略微增加,在迎面风速为2m/s时,积灰0.1 mm比积灰0 mm增加0.013%,积灰0.3 mm比积灰0.1 mm增加0.031%,与文献[8]的计算结果差别不大。由于空气流过翅片区域时,积灰后的速度比积灰前的速度略微增大,管外对流换热系数也略微增加。

图9 积灰前后对流换热系数

图10 积灰前后传热系数
由图10可以看出,随着迎面风速的增加,积灰前后5种工况下的传热系数也逐渐增加,且每种工况下的增大速度逐渐变缓;在同一迎面风速下,随着积灰厚度的增加,传热系数呈逐渐下降的趋势,如在迎面风速为2 m/s时,积灰0.1 mm比积灰0 mm减小0.021%,积灰0.3 mm比积灰0.1 mm减小0.036%。传热系数随着翅片管表面积灰厚度的增大而减小,说明了翅片管表面积灰影响了凝汽器的换热,降低了积灰单元的换热能力。由此可知,在运行中,除了需要保证一定的迎面风速,更要保持凝汽器的清洁,经常性地进行除灰措施。
由图11可知,随迎面风速的增大,积灰前后5种工况下翅片管进出口的压力降ΔP也随着增大,并且增加趋势也上升;在同一迎面风速下,随着积灰厚度的增加,压力降ΔP也逐渐增加,如在迎面风速为2 m/s时,积灰0.1 mm比积灰0 mm增加10.173%,积灰0.3 mm比积灰0.1 mm增加37.698%。随着风速的增大,流动阻力也增加,这就意味着需要更多的风机能耗,因此,通过增大迎面风速来提高直接空冷凝汽器的运行效率,也就必须考虑流动阻力的影响。
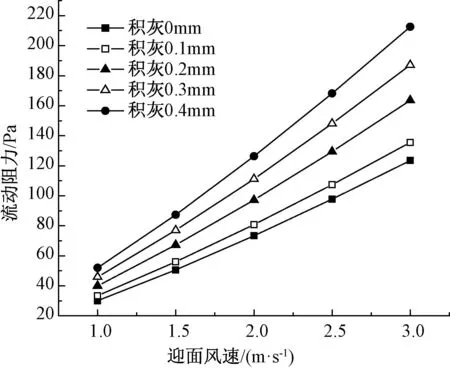
图11 积灰前后流动阻力
根据公式(18)、(20)和(21),计算得到摩擦因子,努塞尔数和雷诺数之间的关系,分别表示在图12和图13上。
从图12和图13可以看出,f随Re的增加而减小,尤其在Re较低的情况下,减小的趋势更大,而Nu随Re的增加而增大;随着积灰厚度的增加,f逐渐增大,Nu逐渐减小,说明随着翅片管束积灰厚度的增加,翅片管的综合热力能力下降。
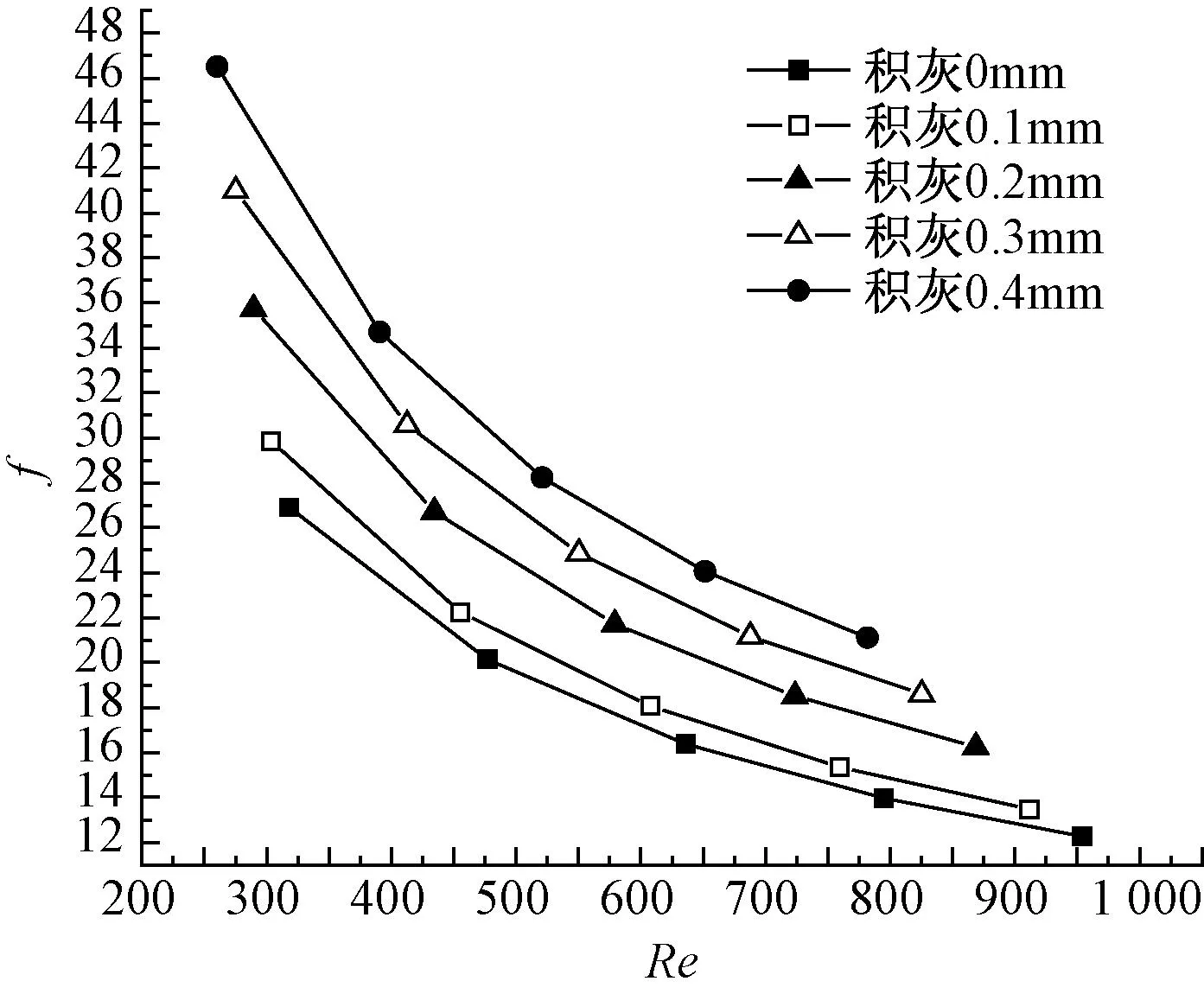
图12 摩擦因子随雷诺数的变化关系
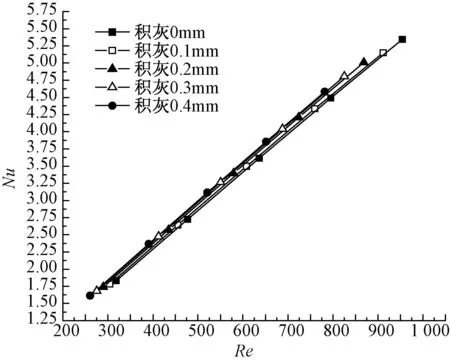
图13 努塞尔数随雷诺数的变化关系
3.2 特征数关联式
采用最小二乘拟合的原理,对通过数值模拟得到的对流换热系数、传热系数、流动阻力随迎面风速的变化关系以及摩擦系数、努塞尔数随雷诺数的变化关系拟合为指数函数形式,列于表2、表3中。

表2 迎面风速表示的翅片管束流动换热关联式
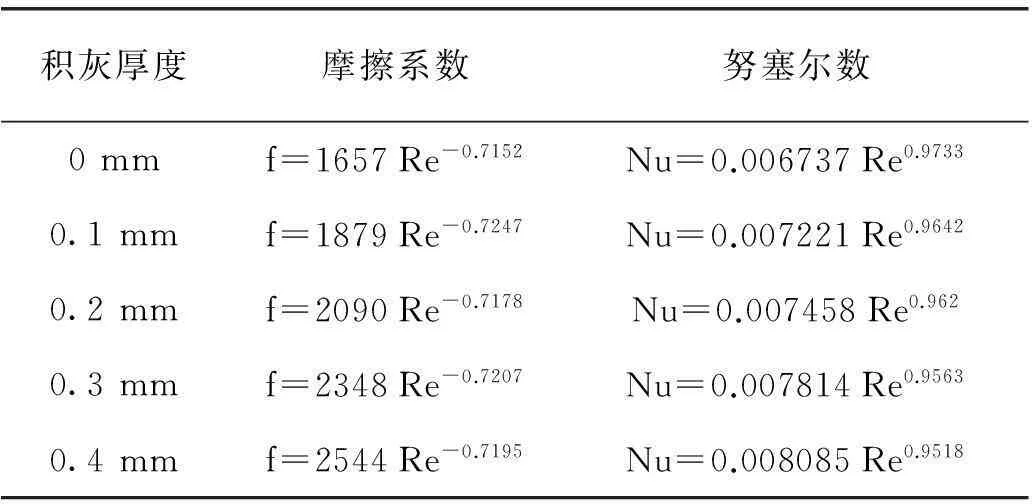
表3 雷诺数表示的翅片管束特征数关联式
4 结论
本文建立翅片管束积灰前后的数值模型,利用FLUENT针对积灰0~0.4 mm 5种工况,进行数值模拟,研究了迎面风速对翅片管流动换热特性的影响,得出结论如下:
(1)以2 m/s迎面风速为例,对比散热管束积灰前后的压力场、速度场、温度场分布。积灰后的入口处压力比积灰前的要大;积灰后与积灰前相比,后半部分高温区域的面积略微增大;空气流经翅片的整个过程,流速呈先增大后减小的趋势,且积灰后,空气流经翅片管的速度变大。
(2)随着迎面风速的增加,翅片管外空气侧对流换热系数、传热系数以及ΔP呈逐渐增大的趋势;在同一迎面风速下,随着积灰厚度的增加,管外对流换热系数略微增加,传热系数下降,ΔP增大。
(3)f随Re的增加而减小,尤其在Re较低的情况下,减小的趋势更大,而Nu随Re的增加而增大;随着积灰厚度的增加,f逐渐增大,Nu逐渐减小,翅片管束综合热力性能下降。
[1]魏栋,王建平,吴鹏,等. 300MW直接空冷凝汽器污垢热阻对换热面积影响[J]. 电力科学与工程,2012,28(2):51-55.
[2]郭民臣,李美宝,彭新飞,等. 空冷凝汽器积灰对机组出力影响的计算分析[J]. 中国电力,2013,46(9):52-55.
[3]郭民臣,陈文飞. 电站空冷凝汽器积灰的计算分析及监测[J]. 汽轮机技术,2013,55(4):291-294.
[4]丁尔谋. 发电厂空冷技术[M]. 北京: 水利电力出版社,1992:23-32.
[5]杨世铭,陶文铨. 传热学[M]. 北京: 高等教育出版社,2008.
[6]郭民臣,任德斐,李鹏. 空冷凝汽器积灰对运行调节影响的计算分析[J].中国电机工程学报,2012,32(11):52-55.
[7]刘博. 电站汽轮机空冷凝汽器研究[D].武汉:华中科技大学,2007.
[8]王丽,张义江,郭民臣,等. 积灰及迎面风速对直接空冷机组性能的影响[J].中国电力,2015,48(2):21-26.
[9]丁丽媛,陈帅,程友良. 空冷凝汽器U型翅片管水平布置间隙优化[J]. 电力科学与工程,2013,29(9):62-69.
[10]周兰欣, 乔瑾, 张淑侠. 600MW机组空冷凝汽器变工况特性计算与研究[J].华北电力大学学报(自然科学版),2011,38(1):92-97.
[11]代善良. 迎面风速对直接空冷凝汽器流动换热特性的影响[D].哈尔滨:哈尔滨工业大学,2013.
[12]陈文飞. 空冷凝汽器翅片管积灰对换热的影响特性研究[D]. 北京:华北电力大学,2013.
[13]杨立军,杜小泽,杨勇平,等.火电站直接空冷凝汽器积灰检测[J].热能动力工程,2007,22(2):172-175.
[14]杨立军, 周健, 杜小泽,等. 扁平管外蛇形翅片空间的流动换热性能数值模拟[J].工程热物理学报,2007,28(1):122-124.
[15]LIN C N.Heat transfer and fluid flow analysis for plate|fin and oval tube heat exchangers with vortex generators[J].Heat Transfer Engineering,2008,29 (7):588-596.
[16]LI L,DU X,YANG L,et al.Numerical simulation on flow and heat transfer of fin structure in air-cooled heat exchanger [J].Applied Thermal Engineering, 2013,59(s1-2):77-86.
《电力科学与工程 》
欢迎投稿
欢迎订阅
投稿网址:http://www.dlkxygc.com
Study on Heat Transfer Characteristics of Dust Accumulation on Direct Air-cooled Condenser Fin
ZHANG Xuelei, SUN Miaoqing,GE Yongjian,DUAN Junyang
(School of Energy Power and Mechanical Engineering, North China Electric Power University, Baoding 071003,China)
In order to study the heat transfer and its flow characteristics of dust accumulation on direct air-cooled condenser cooling tubes, the heat transfer and flow condition of the different thickness of the fin tube were simulated by FLUENT software, and the distribution of the pressure, temperature and velocity of different thickness of the fin tube were compared and analyzed. The variations of the convective heat transfer coefficient, heat transfer coefficient and flow resistance of the five kinds of ash deposits with the windward velocity were presented, and the correlating equations of the friction factor versus Reynolds number and the Nusselt number versus Reynolds number were obtained by fitting. The results show that the convective heat transfer coefficient, heat transfer coefficient, and flow resistance before and after the deposition of ash grow gradually with the increase of the wind speed. Under the same windward velocity, convective heat transfer coefficient and flow resistance are enhanced and heat transfer coefficient drops with the increase of the thickness of the ash.
flat wave finned tube;head wind speed;ash deposition thickness;flow heat transfer characteristics
2016-01-18。
中央高校基金科研业务费专项资金资助(2015MS116)。
张学镭(1977-),男,副教授,从事电站冷端系统优化运行关键技术、先进能源动力系统的建模与优化等方面的研究工作,E-mail:xueleizh@163.com。
TK267
A
10.3969/j.issn.1672-0792.2016.03.012
