内压作用下CPR1000安全壳的破坏机理研究
2016-04-25易平王庆康刘君
易平, 王庆康, 刘君,2
(1. 大连理工大学 建设工程学部,辽宁 大连 116024; 2. 大连理工大学 海岸与近海工程国家重点实验室,辽宁 大连 116024)
内压作用下CPR1000安全壳的破坏机理研究
易平1, 王庆康1, 刘君1,2
(1. 大连理工大学 建设工程学部,辽宁 大连 116024; 2. 大连理工大学 海岸与近海工程国家重点实验室,辽宁 大连 116024)
摘要:核反应堆安全壳是核电厂中防止放射性物质外泄的最后一道屏障,在发生LOCA 等设计基准事故时,若安全壳承受的内压不超过设计压力,安全壳混凝土不应出现裂缝。以实际CPR1000安全壳为研究对象,按照预应力筋实际情况建立三维非线性有限元数值模型,着重探讨了安全壳中预应力筋与混凝土之间相互作用的模拟方法,分析了安全壳施加内压前后预应力筋内力变化情况,验证了本文所提方法的准确性。给出了安全壳在内压作用下的破坏模式和薄弱部位,为安全壳的分析和设计提供依据。
关键词:核电厂;CPR1000安全壳;预应力筋;数值分析;破坏机理;内压
核能不仅单位能量大,而且资源丰富,是公认的唯一现实的可大规模替代常规能源的清洁、经济能源。目前我国在建核电机组共29台,在建规模世界第一[1]。预应力筋混凝土安全壳(简称安全壳)是核反应堆的最后一道屏障,其主要用途是屏蔽发生基准失水事故时产生的辐射物质,防止外物的袭击等,应该具有承受内压而不出现混凝土裂缝的能力[2]。日本福岛核电厂事故表明,核电厂安全壳承受事故内压的能力十分重要,因此,对核电厂安全壳的研究就显得尤为迫切。
夏祖讽等[3]采用杆单元模拟预应力筋对先进核电厂安全壳进行了有限元分析,得到了合理的安全壳预应力张拉顺序以及安全壳在设计事故内压、严重事故内压状态下的工作性能和极限承载能力,并与1∶10的大比尺结构模型试验结果进行了比较。陈勤等[4]则采用空间曲面膜单元来模拟预应力筋。Yonezawa等[5]也采用杆单元模拟预应力筋,建立了2个有限元模型:360°壳单元模型和轴对称模型,通过调整预应力筋和混凝土之间的摩擦影响,分析研究了安全壳在内压作用下的极限承载力。在这些分析中,对安全壳中预应力筋的模拟都采用了简化的方式,在安全壳局部应力方面分析的不够。
本文将以中国改进型压水堆核电厂(CPR1000)[6]实际安全壳为研究对象,严格按照安全壳中预应力钢筋的布置方式,采用更合理的方法模拟预应力钢筋与混凝土之间的相互作用;通过详细的三维有限元计算,给出不同内压水平下预应力筋的内力分布、安全壳的薄弱部位、安全壳的开裂发展过程等。
1CPR1000安全壳组成
CPR1000安全壳结构由底板、筒体和穹顶组成,如图1所示。安全壳内径37 m,筒体部分高50.11 m,底板底面至穹顶的总高66.68 m,筒体的正常壁厚0.9 m,穹顶的正常厚度0.8 m,在标高22.9 m方位角0°位置设有一直径7.4 m的设备孔。筒体外侧设置了4个互成90°的扶壁柱。筒体部分设有2层环向及一层竖向预应力钢束,竖向钢束的上端锚固在环梁的顶面,下端则锚固在安全壳底板上。穹顶部分则布置了3层预应力钢束,钢束锚固在环梁上。预应力钢束采用1 860级预应力钢绞线,采用后张法施加预应力。竖向预应力钢束横截面积为5 400 mm2,数量为144根;环向预应力钢束横截面积为2 850 mm2,数量为223根;穹顶预应力钢束与筒体的环向预应力钢束相同,数量为174根[7]。安全壳混凝土内还配置有HRB400普通钢筋,筒体普通钢筋的竖向体积配筋率为1%,环向配筋率为2%,穹顶互成90°角的配筋率各为2%。在安全壳内部还有一层6 mm厚的钢衬里,钢衬里采用铆钉与混凝土壳紧密连接。

图1 安全壳结构组成Fig.1 Composition of containment structure
2三维数值模型的建立
本文采用ANSYS软件对CPR1000安全壳进行非线性有限元分析。安全壳有限元网格如图2所示。

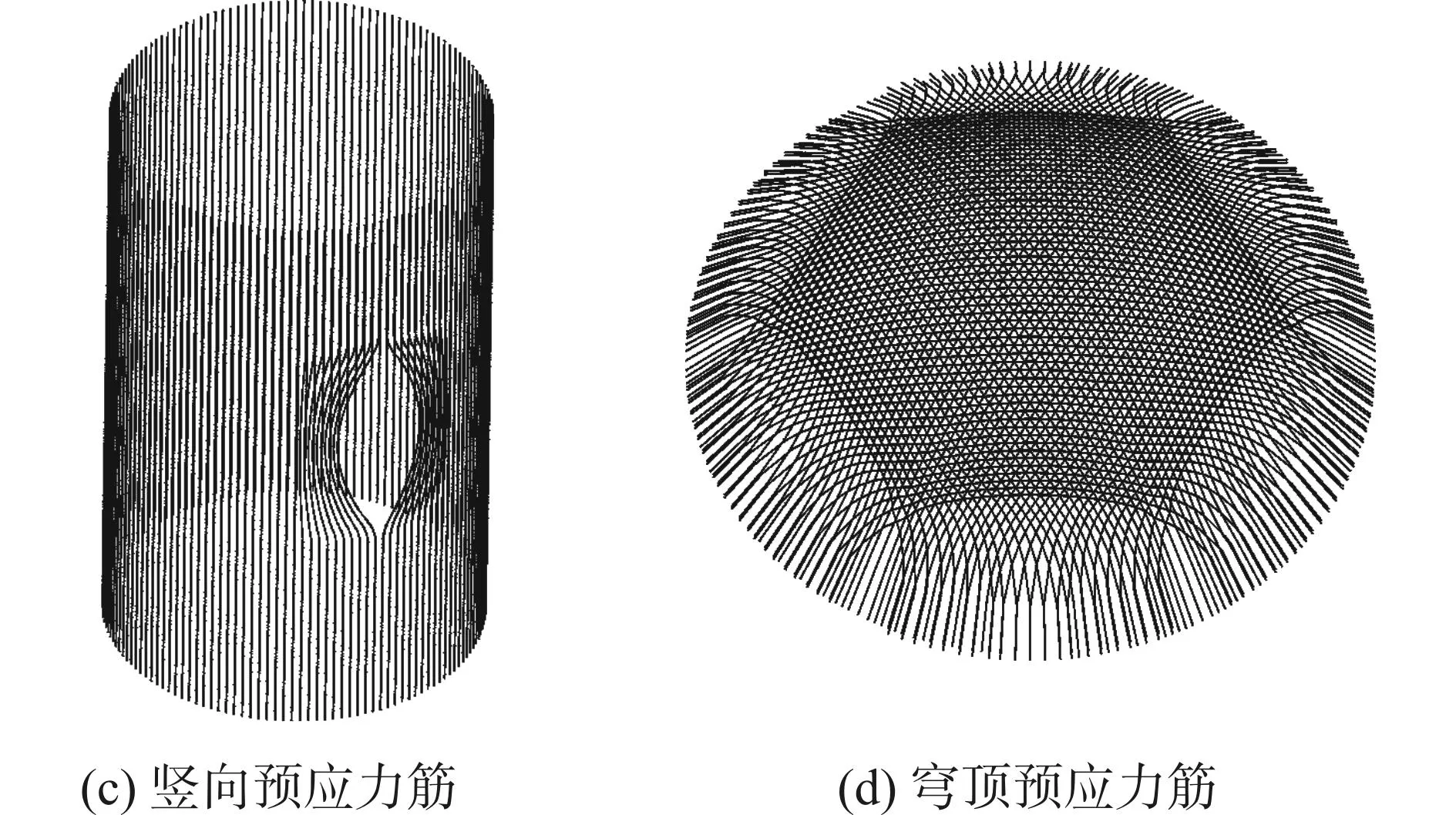
图2 安全壳计算模型Fig.2 Containment numerical model
安全壳的底板、筒体和穹顶采用3D加筋混凝土实体单元(SOLID65)模拟,预应力筋采用只受拉的杆单元(LINK180)模拟,钢衬里采用壳单元(SHELL181)模拟。
2.1模型建立
2.1.1 混凝土和预应力筋之间的相互作用模拟
混凝土与预应力筋之间相互作用的模拟方法大致有2种:等效荷载法和实体力筋法[8]。等效荷载法虽然网格划分简单,不必考虑预应力筋的位置直接建模,但张拉过程难以模拟,无法模拟应力损失引起力筋各处应力不同的情况。当预应力筋布置复杂时,很难用合适的外荷载代替预应力的作用,尤其是无法真正模拟预应力筋与混凝土结构之间的相互作用。实体力筋法是用杆单元在预应力筋的实际位置模拟预应力筋,预应力的模拟可采用降温法和初应变法。实体力筋法可消除等效荷载法的缺点,对预应力混凝土结构的应力分析能够比较精确地模拟。该方法在有限元建模时有三种处理方法,即实体切分法、节点耦合法和约束方程法[9]。
1) 实体切分法:基本思路是先以混凝土结构的几何尺寸创建实体模型,然后用工作平面和预应力筋线拖拉形成的面切分实体,用切分后体上与预应力筋线相同位置的线定义预应力筋。这种方法是基于几何模型的处理,力筋位置精确,求解结果精确,但当预应力筋线型复杂时,建模麻烦。
2) 节点耦合法:基本思路是分别建立实体和预应力筋的几何模型,各自独立划分单元,然后采用耦合节点自由度将预应力筋单元和实体单元联系起来。采用此种方法需要将混凝土单元划分的很密,这样一来,计算代价将会很高,计算效率很低。由于安全壳中预应力筋较多且密,建立准确的自由度耦合非常不易。
3) 约束方程法:类似于节点耦合法,只是在联系混凝土单元和预应力筋单元的时候是选择预应力筋的节点,通过CEINTF命令自动选择混凝土单元的数个节点与预应力筋的一个节点建立约束方程,通过建立多组约束方程,将预应力筋单元和混凝土单元联系起来。由于安全壳中预应力筋很多(541根),更由于安全壳形状都为曲面,模拟预应力筋的杆单元的数量非常大,要保证每个预应力筋的节点与混凝土相应的节点之间建立准确的约束方程几乎是不可能的。
为了能较好模拟预应力筋与混凝土之间的相互作用,保证所建立的模型能准确反映工程实际,在忽略混凝土和预应力筋之间的粘结滑移作用情况下,本文提出了一种建立安全壳有限元模型的方法。首先采用杆单元建立预应力筋的有限元模型,然后沿安全壳筒壁和穹顶的厚度方向复制预应力筋节点,在复制的层与层节点之间建立混凝土单元。此种方法保证了力筋节点和混凝土节点之间的共同作用,避免了混凝土单元细化的要求,很好地模拟了预应力筋和混凝土之间的相互作用。
2.1.2普通钢筋
普通钢筋的模拟采用整体式模型,也称分布式模型或弥散式模型,即将钢筋连续均匀分布于实体单元中,整体式模型综合了钢筋对刚度的贡献。对SOLID65单元来说,通过设定2个正交方向的体积配筋率来考虑钢筋的贡献。
2.2边界条件
安全壳底板底部节点的自由度全部约束,在模拟钢衬里的SHELL181单元上施加均布的内压,内压共分十级,每级0.1 MPa。
2.3计算规模
由于安全壳结构复杂,预应力筋很多,且布置复杂,本文采用较多的单元类型和数量来建立一个比较符合实际的安全壳模型,具体计算规模见表1。
2.4材料模型
2.4.1混凝土
混凝土强度等级为C50,计算中混凝土弹性模量Ec=34.5 GPa,泊松比υc=0.2,密度ρc=2 500 kg/m3。混凝土采用多线性随动强化模型,应力应变关系如图3所示。混凝土的单轴应力应变关系上升段采用GB50010-2010[10]规定的公式,下降段则采用Hongnestad[11]的处理办法,即
(1)
(2)

表1 CPR1000安全壳模型计算规模

图3 混凝土应力应变关系Fig.3 Stress-strain relationship of concrete
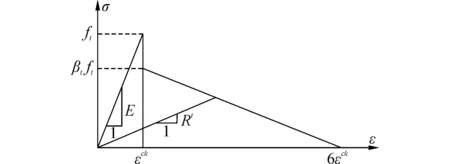
图4 Rt示意图Fig.4 Schematic diagram of Rt
2.4.2预应力筋、普通钢筋和钢衬里
预应力筋、普通钢筋和钢衬里的应力应变关系均采用理想弹塑性模型,其材料参数见表2。

表2 预应力筋、普通钢筋和钢衬里材料参数
3 计算过程及结果分析
整个计算模拟了安全壳的施工过程,分为3步:1)计算安全壳在自重作用下的响应;2)施加预应力;3)施加内压。
3.1 预应力筋的内力
预应力筋与混凝土之间相互作用的模拟方法是否合理可以从预应力筋单元的内力上反映出来,如果每根预应力筋杆单元的内力基本一致,表明模拟方法是准确的。各类型所有预应力筋单元在仅有预应力、预应力+0.4 MPa内压(设计内压值)、预应力+0.6 MPa内压、预应力+0.8 MPa内压4种工况下的内力沿环向的分布情况如图5所示。

(a) 竖筋内力 (b) 环向筋内力 (c) 穹顶筋内力图5 预应力筋单元内力分布Fig.5 The distribution of axial forces of the tendon elements
由图5可以看出,各预应力筋单元的内力分布基本一致。各类型预应力筋单元内力的最大值、最小值、均值以及相对偏差(最大值与最小值之差)如表3所示,最大相对偏差基本都在6%以内。最大相对偏差11.4%发生在竖向预应力筋单元上,主要发生在设备孔周围(如图5所示),这是由于这里的预应力筋弯曲比较厉害造成的。计算结果表明本文采用的预应力筋与混凝土相互作用的模拟方法是可行且合理的。随着内压的施加,预应力筋单元的内力逐步增加,表明预应力筋对安全壳承受内压起到了很大的作用。

表 3 预应力筋轴力对比
3.2混凝土部分的应力分布
图6给出了内压作用下安全壳最大主应力沿360°展开的分布规律。在0.4 MPa内压作用下,拉应力较大的区域集中在设备孔周围、扶壁柱、环梁附近和筒体底部的位置,最大拉应力出现在设备孔上下两侧,但小于混凝土的抗拉强度。穹顶最大主应力分布比较均匀。当内压增大到0.5 MPa时,设备孔上下两侧的拉应力进一步增大,达到了抗拉强度,此时会有裂缝的产生,见图7(a)。当内压达到0.8 MPa时,设备孔几乎被高拉应力区所环绕。穹顶上拉应力区集中程度更加明显了,这些高应力区域是穹顶预应力筋比较少的位置,如图2(d)所示区域。
3.3混凝土的开裂过程
在各级内压作用下安全壳混凝土的开裂情况如图7 所示。在内压为0.4 MPa(设计内压值)时,安全壳混凝土没有开裂发生;当内压达到0.5 MPa时,设备孔上下侧出现局部开裂,范围很小;随着内压增大,设备孔上下侧的裂缝进一步扩展;当内压达到0.8 MPa时,设备孔左右两侧也出现了裂缝,上下侧裂缝进一步扩展,开裂严重,安全壳混凝土失去了它的功能。
3.4 钢衬里应力分析
安全壳内部设有6 mm厚的钢衬里,其作用是在安全壳发生事故时防止辐射物质的扩散,即保证安全壳的密闭性。图8给出了各级内压作用下钢衬里第一主应力沿360°展开的分布情况。在仅有预应力作用下,钢衬里第一主应力分布均匀(如图8(a)所示),处于受压状态。最大应力发生在安全壳底板与柱体斜坡交界处,这是由于此处的突然转折引起的。在环梁与筒体交界处,由于穹顶预应力筋和竖向预应力筋的作用,使得此处所受压应力较大。;当内压达到0.8 MPa时,孔口部位的最大拉应力达到120 MPa (图8(b));而当内压达到1.0 MPa时,孔口部位的最大拉应力已达到294 MPa (图8(c)),但还低于钢衬里材料的屈服极限,还能够保持它的设计功能。钢衬里应力的快速增长,是与混凝土的损伤开裂密切相关的。由于在0.8 MPa下,孔口附近的混凝土出现了加大范围的损伤开裂 (图6(b)),因此在1.0 MPa下,钢衬里的应力较0.8 MPa时的应力增加了近1.5倍。

(a) 0.4 MPa (b) 0.5 MPa (c) 0.8 MPa图6 内压作用下筒体最大主应力云图Fig.6 Maximum stress contours of cylinder

图7 安全壳混凝土开裂Fig.7 Concrete crack in containment

(a) 仅预应力作用下第一主应力云图
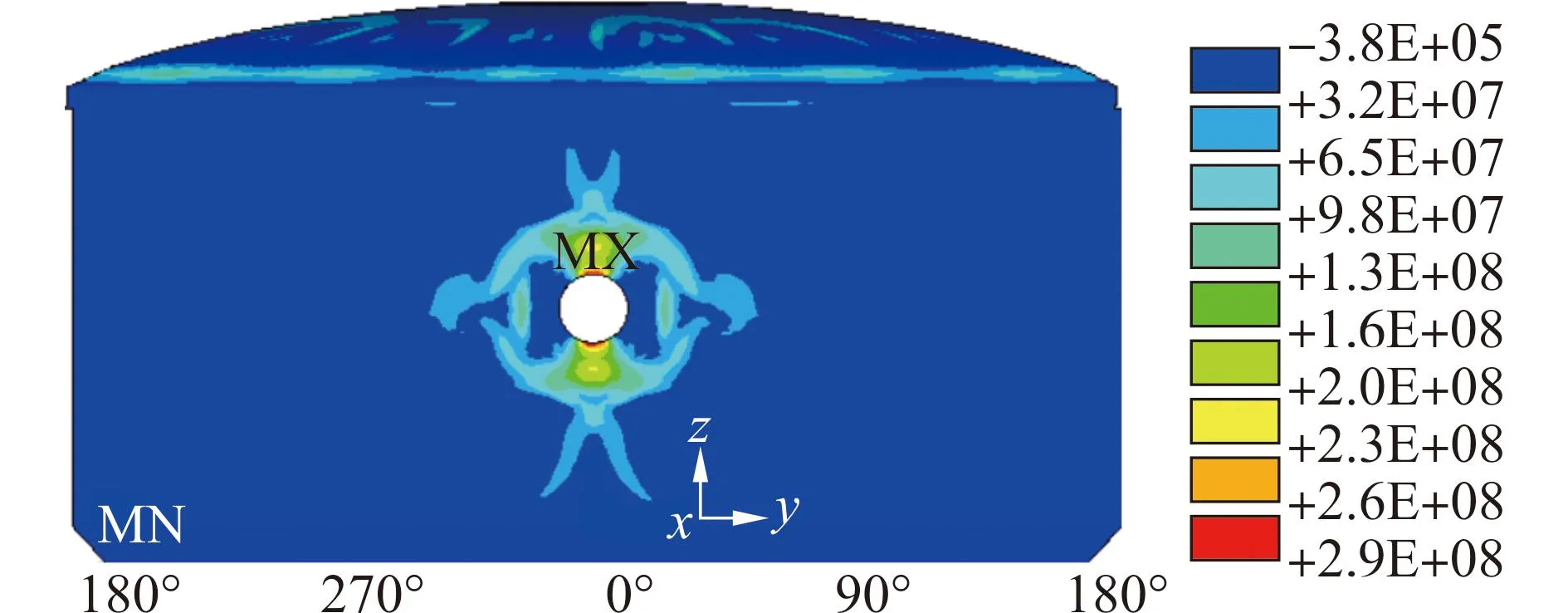
(c) 1.0MPa内压作用下第一主应力云图图8 钢衬里应力云图Fig.8 Stress contours of steel lining
4结论
本文给出了能较好模拟预应力混凝土安全壳的有限元分析方法,针对实际的CPR1000安全壳进行了详细的内压分析,从计算结果分析可得出以下结论:
1) 本文所采取的安全壳建模方法能很好地模拟预应力筋与混凝土之间的相互作用,能够较好的反映安全壳在内压作用下的应力分布及开裂位置。
2) 在内压作用下应力较大的区域集中在扶壁柱、设备孔周围、环梁附近和筒体底部的位置,这些部位应是核电厂安全壳的薄弱部位,尤其是设备孔周围和基底部位应予以重视。
3) 在0.4 MPa设计事故内压作用下,安全壳没有开裂,满足核电厂安全壳的设计使用要求。随着内压的增大,安全壳首先在设备孔上下侧开裂,并逐步扩展,然后设备孔左右两侧也出现了裂缝,在0.8 MPa时,孔口附近的混凝土开裂严重,但钢衬里的最大应力仍然小于材料的屈服极限,安全壳还可以起到它防辐射的功能。
参考文献:
[1]尚海. 张华祝: 我国核电站的在建规模保持世界第一[J]. 广西电业, 2013 (6): 8.
SHANG Hai. Zhang Huazhu: China's nuclear power plants under construction is keeping the world's first[J]. Guangxi electric power, 2013 (6): 8.
[2]李冬梅. 某核电站安全壳的隔震地震反应分析[D]. 哈尔滨: 哈尔滨工程大学, 2007: 33-46.
LI Dongmei. Seismic analysis of a reinforced concrete containment vessel on isolating devices[D]. Harbin: Harbin Engineering University, 2007: 33-46.
[3]夏祖讽, 王明弹, 黄小林, 等. 百万千瓦级核电厂安全壳结构设计与试验研究[J]. 核动力工程, 2002, 23(S): 123-129.
XIA Zufeng, WANG Mingdan, HUANG Xiaolin, et al. Design research & model experiment of containment in 1000MW NPP[J]. Nuclear power engineering, 2002, 23(S): 123-129.
[4]陈勤, 钱稼茹. 内压荷载下安全壳1: 10模型结构非线性有限元分析[J]. 工程力学, 2002, 19(6): 73-77.
CHEN Qin, QIAN Jiaru. Nonlinear finite element analysis of 1: 10 containment model structure subjected to internal pressure[J]. Engineering mechanics, 2002, 19(6): 73-77.
[5]YONEZAWA K, IMOTO K, WATANABE Y, et al. Ultimate capacity analysis of 1/4 PCCV model subjected to internal pressure[J]. Nuclear engineering and design, 2002, 212(1/3): 357-379.
[6]中国广东核电集团有限公司. 中国改进型压水堆核电站CPR1000简介[J]. 现代电力, 2006, 23(5): 36-38.
[7]龚振斌. 核电站安全壳预应力工程[C]//新世纪预应力技术创新学术交流会论文集. 北京: 中国土木工程学会, 2002: 515-522.
GONG Zhenbin. Prestress engineering in nuclear power plant containment[C]//Academic Conference Proceedings of Prestressed Technology Innovation in the New Century. Beijing: Civil Engineering Society of China, 2002: 515-522.
[8]张耀庭, 邱继生. ANSYS在预应力钢筋混凝土结构非线性分析中的应用[J]. 华中科技大学学报:城市科学版, 2003, 20(4): 20-23.
ZHANG Yaoting, QIU Jisheng. Application of ANSYS in nonlinear analysis of prestressed reinforced concrete structure[J]. Journal of Huazhong university of science and technology: urban science edition, 2003, 20(4): 20-23.
[9]王新敏. ANSYS工程结构数值分析[M]. 北京: 人民交通出版社, 2007: 487-489.
[10]中华人民共和国住房和城乡建设部. GB 50010-2010, 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2010.
Ministry of Housing and Urban-Rural Construction of the People's Republic of China. GB 50010-2010, Code for design of concrete structures[S]. Beijing: China Architecture Industry Press, 2010.
[11]HOGNESTAD E. A study of combined bending and axial load in reinforced concrete members[J]. University of Illinois Bulletin,1951, 49(22): 123-128.
[12]李围. ANSYS土木工程应用实例[M]. 2版. 北京: 中国水利水电出版社, 2007: 80.
Research on failure mechanism of CPR1000 containment vessel under internal pressure
YI Ping1,WANG Qingkang1,LIU Jun1,2
(1. Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, China; 2. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China)
Abstract:The containment vessel of a nuclear reactor is the last barrier to prevent leaks of radioactive substance in a nuclear power plant. It should be able to withstand the internal pressure with no concrete cracks appearing during a loss-of-coolant accident. This paper takes CPR1000 containment vessel as the research object, and a 3D nonlinear finite element numerical model is established according to the practical condition of prestressed tendons. This paper discussed simulation method of interaction between prestressed tendon and concrete, and compared internal force of prestressed tendon before and after the internal pressure is added to the containment vessel, which has verified the correctness of the method proposed in this paper. This paper has given the damage mode and weak parts of containment vessel under the action of internal pressure, which provides a basis for analysis and design of the containment vessel.
Keywords:nuclear power plant; CPR1000 containment; tendons; numerical analysis; failure mechanism; internal pressure
中图分类号:TL364+.3
文献标志码:A
文章编号:1006-7043(2016)02-0162-06
doi:10.11990/jheu.201409056
作者简介:易平(1973-), 女, 副教授;通信作者:刘君,E-mail: junliu@dlut.edu.cn.
基金项目:国家自然科学基金资助项目(51138001,11102033).
收稿日期:2014-09-23.网络出版日期:2015-12-15.
网络出版地址:http://www.cnki.net/kcms/detail/23.1390.u.20151215.1141.026.html
刘君(1972-), 男, 教授,博士生导师.
