公切线式双圆弧齿廓谐波齿轮传动设计*

王家序，周祥祥，李俊阳，肖　科，李　奇

(1．重庆大学 机电传动与运载装备研究所，重庆　400044；2.四川大学 空天科学与工程学院，四川 成都　610065)



公切线式双圆弧齿廓谐波齿轮传动设计*

王家序1,2†，周祥祥1，李俊阳1，肖科1，李奇1

(1．重庆大学 机电传动与运载装备研究所，重庆400044；2.四川大学 空天科学与工程学院，四川 成都610065)

摘要：谐波传动轮齿齿廓对装置啮合性能具有显著影响.为提高谐波传动的啮合性能，采用公切线式双圆弧齿廓作为柔轮齿廓，基于改进运动学理论计算双圆弧齿廓谐波传动共轭区域、共轭齿廓，并采用最小二乘拟合方法对理论共轭齿廓进行圆弧拟合；利用MATLAB对谐波传动侧隙、重合度、装配变形、运动轨迹等进行仿真分析.研究结果表明：所设计的双圆弧谐波传动轮齿啮合连续、啮合点不断改变，且存在“双共轭”现象，理论啮合弧长为109.3 mm，重合度达到69.03，啮合性能显著优于传统渐开线齿廓谐波传动，并且优选径向变形量系数是消除谐波传动啮合干涉的重要方式之一.

关键词：谐波传动；双圆弧齿廓；改进运动学；运动特性

谐波齿轮传动依靠柔轮的可控弹性变形实现与刚轮啮合运动，柔轮与刚轮齿廓对装置啮合性能影响显著.为进一步提高谐波齿轮传动啮合性能，国内外学者对谐波传动轮齿齿廓及其啮合理论进行了大量研究.谐波创始人C.W.Musser从保证传动比要求和使轮齿实现面接触的角度提出基准齿形角为28.6°的直线齿廓，但设计时并未考虑由柔轮变形产生的切向位移与法线转角的影响[1]．Э.М.Цукермац和Г.Е.Неломнящих分别用图解法证明谐波传动可以近似采用渐开线齿形[1]，但渐开线齿形具有重合度较小、波发生器载荷较大及尖点啮合等特点.[2]日本学者S.Ishikawa[3-4]从不需变形而保证连续接触角度提出具有两段圆弧的S齿形，该齿形提高了谐波传动的啮合性能及承载能力，但设计时将轮齿抽象为具有相同齿形的齿条，因而其应用受到局限.目前国内外学者正致力于开发适用于谐波传动的圆弧齿廓谐波传动，圆弧齿谐波传动具有啮合质量良好、柔轮轴向尺寸较小、传动比范围较广等特点.沈允文[5]对上述几种齿形的性能进行了比较，结果表明圆弧齿传动精度高，啮合性能好.辛洪兵等[6]对谐波传动采用圆弧齿廓的合理性进行了证明，并对双圆弧齿廓谐波传动进行设计研究[7].陈晓霞等[8]对双圆弧齿廓参数对传动性能的影响进行了仿真分析.但目前国内对于双圆弧齿廓谐波传动的研究尚不成熟.因此，进一步设计适用于谐波齿轮传动的双圆弧齿廓并对其啮合特性进行分析具有重要的研究价值.

与传统齿轮减速装置相区别[9-10]，目前研究谐波传动啮合理论有代表性的几种基本方法有图解分析法、等速曲线法、包络理论法、幂级数法[1]以及国内由辛洪兵等人较早开始研究的基于改进运动学的理论[11-12].基于改进运动学的理论相对于前几种方法具有几何意义明确、计算简单、啮合矩阵不随共轭曲面形式改变等优点.基于此，本文以公切线式双圆弧齿廓作为设计对象，综合考虑谐波变形因素，基于改进运动学理论对适用于谐波传动的双圆弧齿廓进行设计，并对双圆弧齿廓啮合特性进行分析，为谐波传动设计和分析提供一定参考.

1共轭齿廓设计

以波发生器输入、刚轮固定、柔轮输出、椭圆波发生器作用下的公切线式双圆弧齿廓谐波传动为例，优选齿形参数，结合谐波变形特点设计适用于该谐波传动的双圆弧齿廓柔轮与刚轮，设计参数基本要求见表1.

表1　设计参数

设计假设:

1)传动过程中,柔轮变形前后中性层曲线长度不变；

2)柔轮轮齿工作时形状不变，只有齿槽发生变形；

3)柔轮所有特征圆都是柔轮中线的等距曲线.

1.1柔轮双圆弧齿廓设计

公切线式双圆弧齿廓基本形状如图1所示.[13]

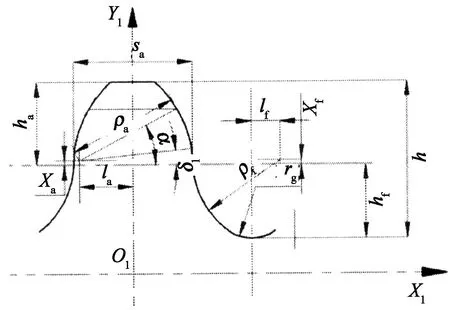
图1　柔轮齿廓

谐波传动原理与一般齿轮传动不同，柔轮齿廓参数受到柔轮可控弹性变形的影响，许多参数不能沿用一般圆弧齿廓参数选取原则，故需在传统圆弧齿廓的基础上结合谐波传动特点对柔轮圆弧齿廓参数进行选择.主要齿廓参数的确定见表2.

表2　柔轮齿廓参数

1.2刚轮齿廓设计

1.2.1柔轮变形形状

根据上文假设，在椭圆波发生器的作用下柔轮中性线为标准椭圆的等距曲线，故柔轮轮齿在波发生器作用下与长半轴角坐标为ψ的点的径向位移w，切向位移v和法向转角μ分别为[7]：

w=ρ-rb,

(1)

v=-∫wdψ,

(2)

(3)

式中：ρ为标准椭圆的极坐标方程；rb为柔轮未变形时的等效圆半径.

谐波传动中，波发生器会迫使柔轮壳体沿轴向产生外张的张角，为了更符合谐波传动实际情况，在设计中考虑壳体张角影响.设柔轮筒体长度为L，则柔轮中线上柔轮轮齿原点O1在柔轮变形后与变形前的径向转角θw与切向转角θv分别为:

θw=w/L，θv=v/L.

(4)

1.2.2柔轮变形形状

建立如图2所示坐标系，以柔轮轮齿对称轴为Y1轴，以Y1轴与柔轮原始曲线交点为坐标原点O1，以原始曲线在O1切线方向为X1轴，根据右手法则确定Z1轴建立柔轮轮齿动坐标系{O1,X1,Y1,Z1}.以竖直方向作为刚轮Y2轴，以刚轮回转中心为原点O2，以柔轮筒体方向为Z2轴，根据右手法则确定X2轴，建立刚轮固定坐标系{O2，X2，Y2，Z2}.

根据谐波传动工作原理，波发生器逆时针转动，柔轮轮齿右侧齿廓与刚轮轮齿左侧齿廓进行啮合传动，在动坐标系{O1,X1,Y1,Z1}中建立柔轮右侧齿廓函数表示如下.

柔轮右侧凸齿廓方程：

rs1=(ρacosαa-la)i+(ρasinαa+hf+δs+

Xa)j+uak,

(5)

ns1=(cosαa)i+(sinαa)j.

(6)

图2　啮合坐标模型

柔轮右侧凹齿廓方程：

ρfsinαf)j+ufk,

(7)

ns2=-(cosαf)i-(sinαf)j.

(8)

基于MATLAB编程计算，将式(1)～(6)代入基于改进运动学法的谐波啮合理论方程[11-12]，即可求出刚轮齿廓与柔轮凸齿廓共轭时柔轮轮齿与波发生器长轴的夹角，记为α，进而可以解出与柔轮凸齿廓共轭的刚轮齿廓数值解.同理，可以解出与柔轮公切线、柔轮凹齿廓共轭时柔轮轮齿与波发生器长轴的夹角α，进而解出与柔轮公切线及柔轮凹齿廓共轭的刚轮齿廓数值解.共轭时的解α的范围就是柔轮齿廓与刚轮齿廓存在共轭啮合的区域，称为共轭区[8].将表2中柔轮齿廓参数代入基于改进运动学理论的谐波共轭方程，以从柔轮齿顶开始计算的齿廓弧长为横坐标，共轭角度为纵坐标，计算得到的共轭区如图3所示.代入解α后计算与柔轮齿廓共轭的共轭齿廓数值解，如图4所示.

从图3可知，公切线双圆弧柔轮齿廓与刚轮齿廓存在两个共轭区，其中一个共轭区较窄，共轭角度为0°～10°，即此时柔轮齿廓与刚轮齿廓在波发生器长轴附近共轭啮合，称为共轭区一；另一个共轭区范围较广，柔轮齿廓与刚轮齿廓共轭角度为20°～65°，称为共轭区二；在共轭区一与共轭区二之间存在一定范围的区域没有共轭角度存在；除此之外，共轭区一以及共轭区二都被分为3个区域，以图中点画线作为分界线，左边为1区，共轭角度与柔轮齿廓的圆弧凸齿廓对应，中间为2区，共轭角度与柔轮齿廓的公切线齿廓对应，右边的3区与柔轮齿廓的圆弧凹齿廓对应；给定柔轮齿廓上一点(对应于弧长S)，有2个共轭角度存在，即柔轮齿廓上同一点与刚轮齿廓先后产生两次啮合传动，给定某一啮合角度α，柔轮齿廓上存在2个点同时满足啮合条件，即对于某一啮合角度，柔轮齿廓上存在不同的2个点同时进入啮合传动；然而，上述特点并不是在所有啮合区内都存在，只有位于刚轮齿顶圆与齿根圆之间的共轭齿廓所对应的共轭区才是有效的，称为有效共轭区.对于共轭区一，柔轮弧长在0～0.865 2mm范围内的共轭区为有效共轭区，对于区域二，柔轮弧长在0～0.611 7mm范围内的共轭区为有效共轭区，在图中以分界点为分界线进行区别.

弧长/mm

X/mm

图4为与图3共轭区对应的共轭齿廓数值解，图中实线对应于共轭区二的共轭齿廓数值解，称为共轭二区齿廓.Y轴坐标较小的共轭二区齿廓对应于柔轮双圆弧齿廓的公切线以及圆弧凹齿廓部分，Y轴坐标较大的共轭二区齿廓对应于柔轮双圆弧齿廓的圆弧凸齿廓部分，点画线对应于共轭区一的共轭齿廓数值解，由上到下依次对应于柔轮圆弧凸齿廓、公切线以及圆弧凹齿廓部分.

由图4可知，为避免齿廓干涉，需取共轭一区齿廓中与柔轮凸齿廓对应的共轭齿廓数值解作为刚轮凹齿廓数值解，取共轭二区齿廓中与柔轮凸齿廓对应的共轭齿廓数值解作为刚轮凸齿廓数值解，由于不能同时选取共轭一区齿廓中与柔轮凹齿廓对应的共轭齿廓数值解作为刚轮凸齿廓数值解，因此，此时选取的柔轮参数不利于双共轭区域的存在.陈晓霞等[8]、辛洪兵等[12]对谐波传动参数影响规律进行了研究 ，结果表明，柔轮齿廓参数是影响共轭齿廓位置、半径的主要因素之一，由此可得，对柔轮双圆弧齿廓参数进行合理设计可以使共轭二区齿廓中与柔轮凸齿廓对应的共轭齿廓数值解与共轭一区齿廓中与柔轮凹齿廓对应的共轭齿廓数值解重合，从而基本保证双圆弧齿廓谐波传动双共轭区域的存在，使得双圆弧齿廓谐波传动具有“双共轭”现象，这种双共轭的特点对于提高谐波传动的精度和扭转刚度具有重要作用.进一步优化后得到的柔轮双圆弧齿廓参数见表3，其对应的共轭齿廓如图5所示，此时基本保证了共轭二区齿廓中与柔轮凸齿廓对应的共轭齿廓数值解与共轭一区齿廓中与柔轮凹齿廓对应的共轭齿廓数值解重合.

表3　优化后柔轮齿廓参数

对优化后的共轭齿廓数值解进行最小二乘圆弧拟合后确定刚轮具体齿廓如图6所示，刚轮齿廓具体参数见表4.计算显示刚轮凹齿廓数据点的拟合最小二乘误差为‖δ‖2=2.0324e-05，刚轮凸齿廓数据点的拟合最小二乘误差为‖δ‖2=1.9579e-05.从工程意义上来讲，上述误差基本可以忽略.

X/mm

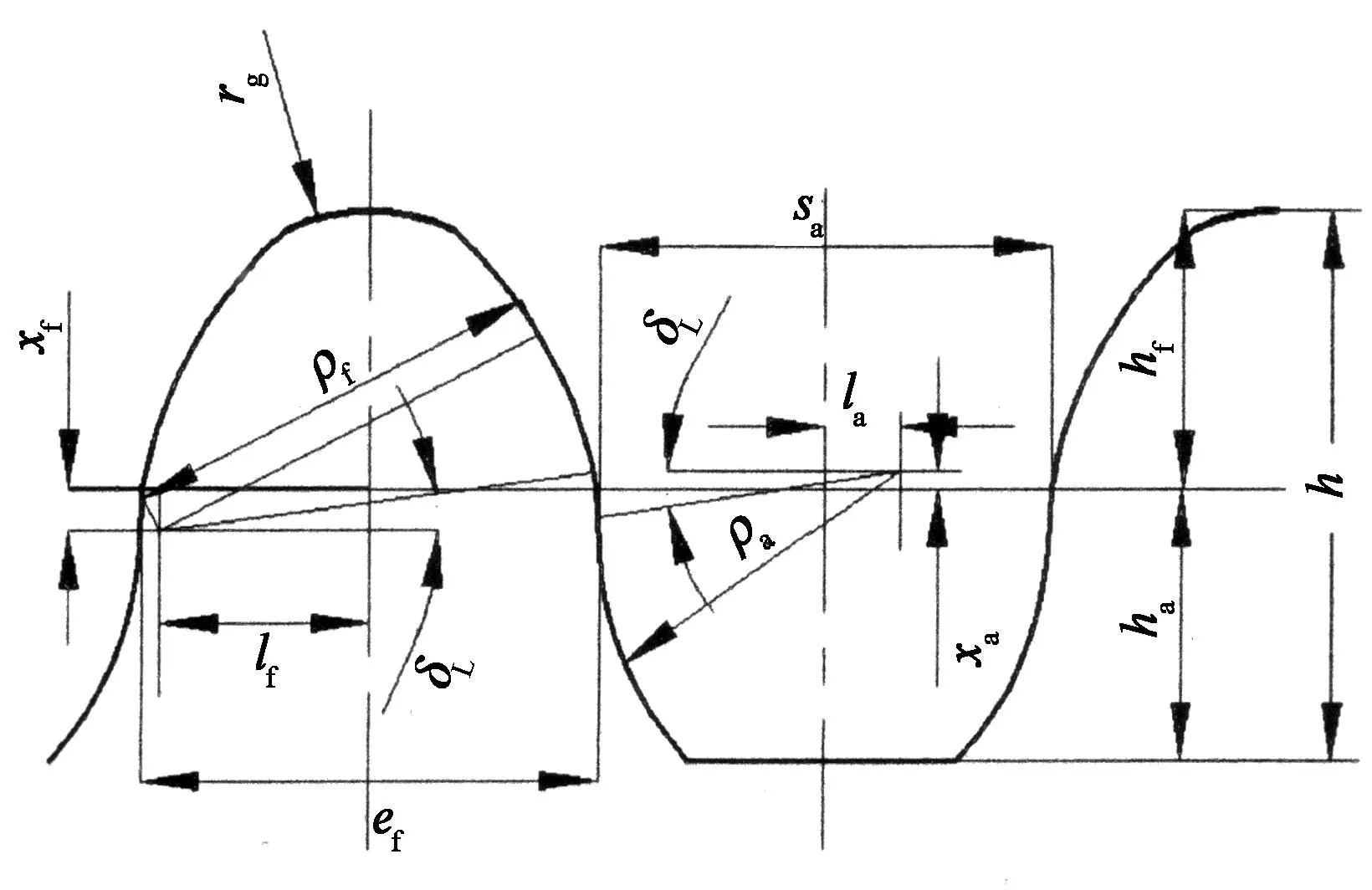
图6　刚轮齿廓

符号意义数值ρa/mmρf/mmrG/mmh/mmhf/mmmδL/(°)sa/mm凸齿齿廓圆弧半径凹齿齿廓圆弧半径齿根圆弧半径全齿高齿根高模数齿形工艺角分度圆齿厚0.6000.6500.3400.950.550.56.750.683

2双圆弧齿廓谐波传动啮合特性分析

2.1谐波传动啮合侧隙与重合度分析

2.1.1啮合侧隙分析

在谐波传动中，对于柔轮轮齿与刚轮轮齿的每个啮合位置(波发生器处于某个转角状态时)，在柔轮工作齿廓上选取一点作为K1，以柔轮回转中心为原点，以原点到K1点的距离为半径做圆弧，与相邻刚轮工作齿廓交于点K2，如图7所示，则K1与K2之间的距离即称为谐波传动在K1点的侧隙[14-15].选取柔轮右侧工作齿廓齿顶坐标作为K1点，以波发生器每转过1°进行迭代计算，绘出双圆弧齿廓谐波传动柔轮右侧工作齿廓齿顶啮合侧隙变化图，如图8所示.

图7　侧隙计算模型

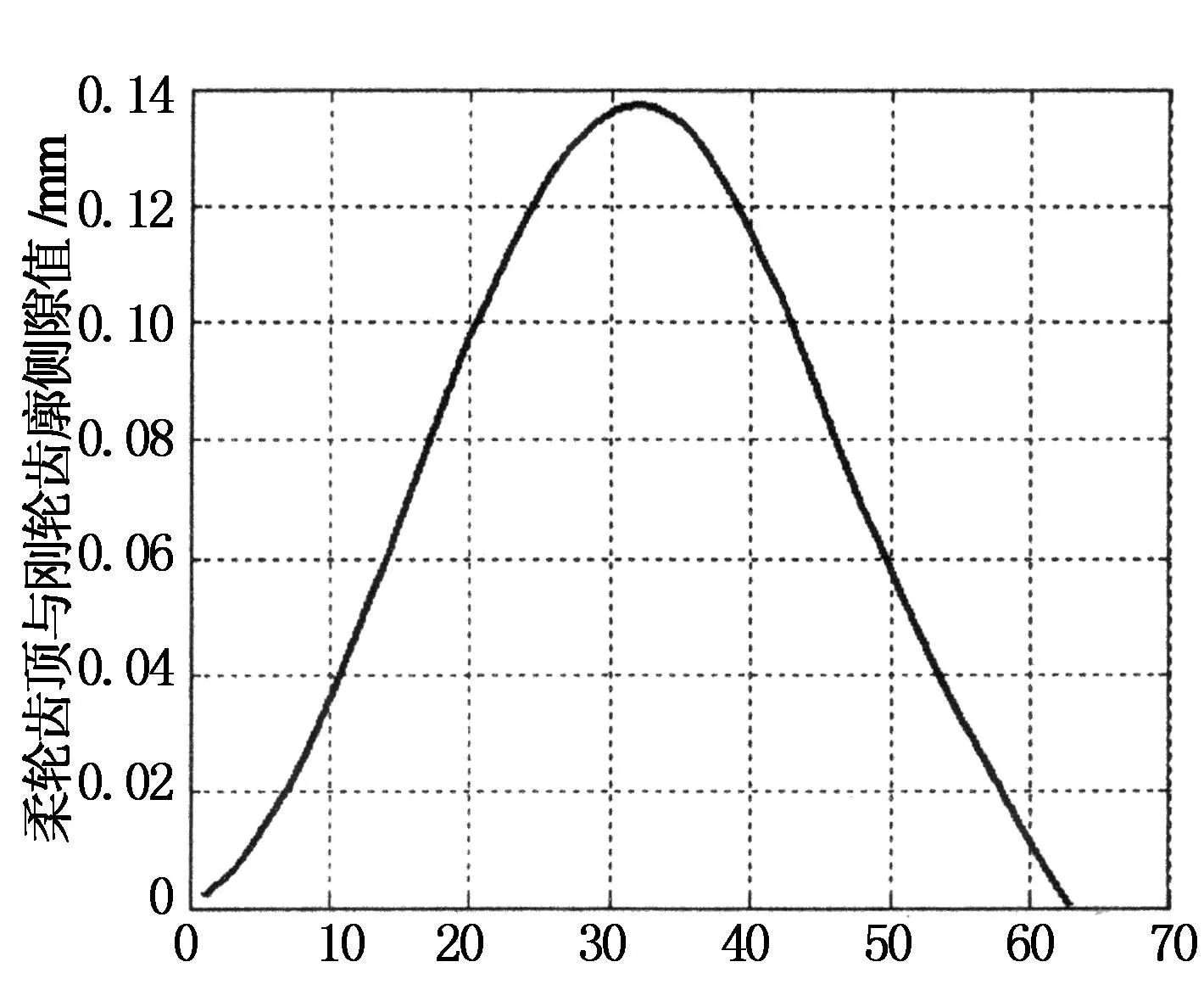
波发生器转角/(°)

由图8可知，柔轮齿顶与刚轮齿廓在啮合过程中的侧隙值始终大于或接近于0，即与刚轮齿不会产生齿廓重迭干涉现象，侧隙值的变化呈现先增大后减小的趋势.波发生器转角为32°时，柔轮齿与刚轮齿之间的侧隙值最大，为0.137 5 mm；当波发生器转角为62°时侧隙最小，约为0 mm，此时柔轮轮齿相对于刚轮齿槽处于刚脱离啮合瞬时，超过62°后柔轮轮齿与刚轮轮齿脱离啮合.

2.1.2重合度分析

谐波传动的重合度实际上指传动过程中同时参与啮合的齿对数[16]，理论啮合弧长是指一对齿从开始啮合到终止啮合时所经过的弧长．对于单波传动，刚脱离啮合时的波发生器转角值就是理论啮合弧长所对应之中心角，记为φea.对于双波传动，理论啮合弧长所对应之中心角φea是轮齿刚脱离啮合时的波发生器转角值的2倍.传动的理论啮合弧长为：

(9)

式中：r2为刚轮分度圆半径.

因此，对于双波传动，理论上可能同时参与啮合的最多齿对数为：

(10)

式中：Pe为柔轮齿顶圆上的齿距.

2.2谐波变形与运动轨迹分析

由于刚轮在工作过程中形状不变，齿廓位置在圆周上环向等角度分布.而变形后柔轮轮齿的齿根位置和方位不断变化，柔轮轮齿的分布不再按环向等角度分布，但柔轮中性层曲线长度基本保持不变，轮齿之间的弧长关系保持不变.在柔轮中装入波发生器后，以波发生器长轴所对应的柔轮轮齿为第1个轮齿，往右依次记为第2，3, … ,n个轮齿，依此类推，按照等弧长分布算法[17-18]，基于MATLAB编程迭代计算后得到双圆弧齿廓谐波传动刚轮与变形柔轮的装配图全图，如图9所示，图中外圈齿廓为刚轮齿廓，内圈齿廓为变形后柔轮齿廓.为更清晰地显示谐波传动轮齿啮合状态，绘制柔轮轮齿与刚轮轮齿局部啮合装配图如图10所示.

X/mm

X/mm

由图9可知，柔轮轮齿在波发生器作用下产生变形后与刚轮轮齿无装配干涉.由图10可知，柔轮轮齿在脱离啮合前与刚轮轮齿啮合状态良好，同时啮合齿数多，啮合点不断改变，因此双圆弧谐波传动具有传动平稳，承载能力较好的特点.

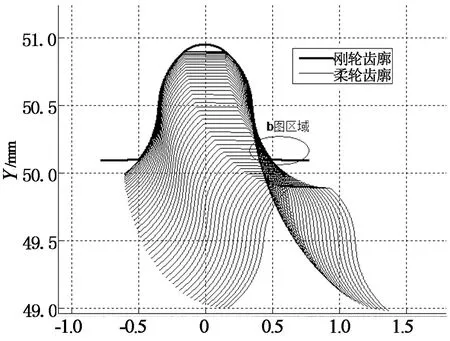
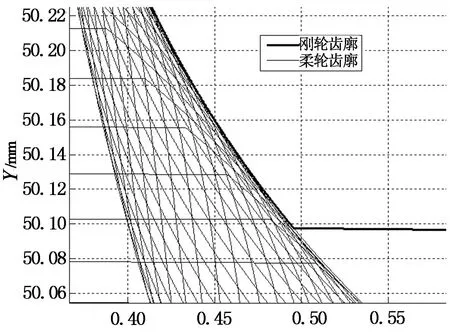
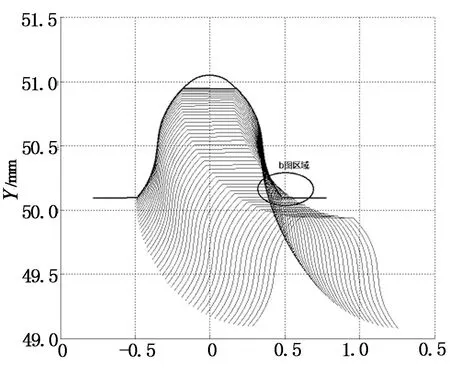
图11为波发生器长轴所对应的第2个柔轮轮齿的啮合情况，由图11可知,柔轮齿廓与刚轮齿廓在A点与B点同时参与啮合,验证了双共轭现象的存在.

X/mm

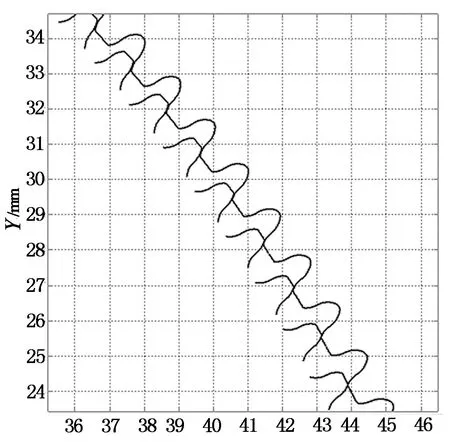
为分析柔轮轮齿相对于刚轮齿槽的运动轨迹，不断改变波发生器转角，对柔轮轮齿齿廓坐标进行坐标变换.得出在波发生器转动90°的过程中柔轮轮齿相对于刚轮齿槽的运动轨迹图形如图12所示.

由图12可知，柔轮轮齿在传动过程中与刚轮轮齿啮合良好，并不存在齿廓干涉，且啮合连续、啮合点不断变化.柔轮轮齿相对于刚轮齿廓的运动轨迹为一内凹曲线.从啮合-啮出-脱开的状态可以看出，在波发生器转动一周的过程中，柔轮轮齿将相对于刚轮转过2个齿，故实现了传动比为100的要求，即谐波传动具有大传动比的特点.将谐波传动径向变形量系数变为1.05，其余参数相同，计算刚轮齿廓并分析此时柔轮轮齿相对于刚轮齿槽的柔轮运动轨迹如图13所示.

X/mm

X/mm

X/mm

X/mm

由图13可知，改变径向变形量系数后，柔轮轮齿与刚轮轮齿在啮合过程中产生了啮入啮出时的齿顶干涉和齿廓重迭干涉.由此可得，在谐波传动设计时，优选径向变形量系数是消除谐波传动啮合干涉的重要方式之一.

3结论

通过对双圆弧齿廓的设计及啮合特性分析, 主要得出如下结论：

1)基于谐波齿轮传动改进运动学啮合理论设计了谐波传动柔轮与刚轮双圆弧齿廓.轮齿在啮合过程中不会发生干涉，并且在柔轮齿未脱离啮合前，柔轮齿廓与刚轮齿廓始终保持正确啮合状态，啮合点不断改变，啮合状态良好，且在传动过程中存在柔轮齿廓与刚轮齿廓“双共轭”的传动区域，可以有效提高谐波传动精度及扭转刚度.

2)所设计的双圆弧齿廓谐波传动当波发生器转角大于62°后柔轮轮齿与刚轮轮齿脱离啮合.且理论啮合弧长为109.3 mm，重合度为69.03，与传统渐开线齿廓谐波传动相比具有理论啮合弧长长，重合度大的特点.

3)径向变形量系数是影响谐波传动的重要因素之一，在谐波传动设计时，优选径向变形量系数是消除谐波传动啮合干涉的重要方式之一.

参考文献

[1]沈允文,叶庆泰. 谐波齿轮传动的理论和设计[M]. 北京：机械工业出版社, 1985:52-68.

SHEN Yun-wen, YE Qing-tai. Theory and design of harmonic drive[M]. Beijing: China Machine Press, 1985:52-68.(In Chinese)

[2]MAITI R, ROY A K. Minimum tooth difference in internal external involute gear pair [J]. Mechanism and Machine Theory, 1996, 31(4):475-485.

[3]ISHIKAWA S. Tooth profile of spline of strain wave: US, 4823638[P]. 1989-04-25.

[4]ISHIKAWA S. Flexing contact type gear drive of non-profile-shifted two-circular-arc composite tooth profile: US, 5458023[P]. 1995-10-17.

[5]沈允文. 论谐波齿轮传动的齿形[J]. 齿轮, 1986, 10 (4): 51-56.

SHEN Yun-wen. Research on tooth profile of harmonic gear drive [J]. Journal of Gear, 1986, 10(4):51-56. (In Chinese)

[6]辛洪兵,何惠阳,谢金瑞. 精密谐波齿轮传动采用圆弧齿廓的合理性证明[J]. 长春光学精密机械学院学报, 1997, 20(3):47-50.

XIN Hong-bing, HE Hui-yang, XIE Jin-rui. Proof of reasonableness of adopting circular arc profile in precision harmonic drive [J]. Journal of Changchun Institute of Optics and Fine Mechanics,1997,20(3):47-50.(In Chinese)

[7]辛洪兵. 双圆弧谐波齿轮传动基本齿廓设计[J]. 中国机械工程, 2011, 22 (6):656-662.

XIN Hong-bing. Design for basic rack of harmonic drive with double-circular-arc tooth profile [J]. China Mechanical Engineering,2011,22(6):656-662.(In Chinese)

[8]CHEN Xiao-xia, LIU Yu-sheng , XING Jing-zhong,etal. The parametric design of double-circular-arc tooth profile and its influence on the functional backlash of harmonic drive [J]. Mechanism and Machine Theory, 2014, 73 (3):1-24.

[9]林超，李莎莎，龚海. 正交变传动比面齿轮的设计及三维造型[J]. 湖南大学学报：自然科学版, 2014, 41(3):49-55.

LIN Chao, LI Sha-sha, GONG Hai. Design and 3D modeling of orthogonal variable transmission ratio face gear [J]. Journal of Hunan University: Natural Sciences, 2014, 41(3):49-55. (In Chinese)

[10]李源，韩旭，叶南海，等. 减速器弧齿锥齿轮动态啮合疲劳强度研究[J]. 湖南大学学报：自然科学版, 2010, 37(6):32-35.

LI Yuan, HAN Xu, YE Nan-hai,etal. Study of the fatigue strength of the dynamic meshing of the spiral bevel gears of reducer [J]. Journal of Hunan University: Natural Sciences, 2010, 37(6):32-35. (In Chinese)

[11]辛洪兵,何惠阳. 谐波齿轮传动共轭齿廓的研究[J]. 长春光学精密机械学院学报, 1996, 19 (2):22-26.

XIN Hong-bing, HE Hui-yang. Study on conjugate profiles of harmonic drive [J]. Journal of Changchun Institute of Optics and Fine Mechanics, 1996, 19(2):22-26. (In Chinese)

[12]辛洪兵. 研究谐波齿轮传动啮合原理的一种新方法 [J]. 中国机械工程, 2002,13(3):181-183.

XIN Hong-bing. A new method for research on engagement principle of harmonic drive [J]. China Mechanical Engineering, 2002,13(3): 181-183. (In Chinese)

[13]邵家辉. 圆弧齿轮[M]. 2版. 北京：机械工业出版社, 1994：76-99.

SHAO Jia-hui. Circular tooth gear[M]. 2nd ed. Beijing: China Machine Press, 1994: 76-99.(In Chinese)

[14]范元勋,王华坤,宋德锋. 谐波传动共轭齿廓的运动学仿真研究[J].南京航空航天大学学报,2002, 34(5):447-450.

FAN Yuan-xun, WANG Hua-kun, SONG De-feng. Kinematics computerized simulation for conjugate tooth profiles of harmonic drive [J]. Journal of Nanjing University of Aeronautics & Astronautics, 2002, 34(5): 447-450. (In Chinese)

[15]范元勋,王华坤,宋德锋. 谐波齿轮传动共轭齿廓的计算机数值模拟研究 [J]. 南京理工大学学报：自然科学版, 2002, 26 (4):389-392.

FAN Yuan-xun, WANG Hua-kun, SONG De-feng. Research on computer simulation for conjugate tooth profiles of the harmonic drive [J]. Journal of Nanjing University of Science and Technology: Natural Sciences, 2002, 26(4):389-392. (In Chinese)

[16]毛彬彬，张石平. 谐波齿轮传动重合度的计算方法研究[J]. 机械设计与制造，2011(7):213-215.

MAO Bin-bin, ZHANG Shi-ping. Research on computing method of contact ratio for harmonic gear drives [J]. Machinery Design & Manufacture, 2011(7):213-215. (In Chinese)

[17]陈晓霞,林树忠,邢静忠,等.圆弧齿廓谐波齿轮侧隙及干涉检查仿真[J].计算机集成制造系统，2011,17(3): 643-648.

CHEN Xiao-xia, LIN Shu-zhong, XING Jing-zhong,etal. Simulation on gear backlash and interference check of harmonic drive with circular-arc teeth profile [J]. Computer Integrated Manufacturing Systems, 2011, 17 (3): 643 -648. (In Chinese)

[18] 陈晓霞,林树忠,邢静忠,等. 基于挠性构件变形的谐波齿轮装配模型[J].计算机集成制造系统,2011,17 (2):338-343.

CHEN Xiao-xia, LIN Shu-zhong, XING Jing-zhong,etal. Assembly model of harmonic gear based on elastic component deformation[J]. Computer Integrated Manufacturing Systems, 2011,17(2):338-343. (In Chinese)

Design of Double-Circular-Arc and Common Tangent Tooth Profile of Harmonic Drive

WANG Jia-xu1,2†, ZHOU Xiang-xiang1, LI Jun-yang1, XIAO Ke1, LI Qi1

(1. Institute of Electromechanical Transmission and Delivery Equipment, Chongqing Univ, Chongqing400044, China;2. School of Aeronautics and Astronautics, Sichuan Univ, Chengdu, Sichuan610065, China)

Abstract:The tooth profile has significant effect on the engagement performance of harmonic drive (HD). In order to improve the engagement quality of HD, double-circular-arc and common tangent tooth profile (DCTP) as the tooth profile of flexspline (FS) were used, the conjugate existent domain (CED) and the conjugate tooth profile were established in Modified Kinematic Method, and the Least-squares fitting approach was adopted to fit it. The backlash, contact ratio, assembly state and relative movement trail were calculated to analyze the meshing performance of HD with a double-circular-arc and common tangent tooth profile. The results have shown that the tooth profile of the FS and the circular spline (CS) used with the DCTP remain continuous engagement, and the engagement point is changed continuously. Moreover, the double-engagement phenomenon is found, the theory conjugate arc length is 109.3mm, and the contact ratio reaches 69.03; compared with the harmonic drive with traditional involute tooth profile, the high engagement performance of harmonic drive can be obtained with the double-circular-arc and common tangent tooth profile. What's more, preferably selecting the coefficient of radial displacement is an important way to eliminate the interference of HD.

Key words:harmonic drive; double-circular-arc tooth profile; modified kinematic method; kinematics character

中图分类号：TH132.43

文献标识码：A

作者简介：王家序(1954-)，男，重庆万州人，重庆大学教授，博士生导师†通讯联系人，E-mail: jxwang@cqu.edu.cn

基金项目：国家自然科学基金资助项目(51435001,51375506) , National Natural Science Foundation of China(51435001,51375506)；国家高技术研究发展计划(863计划)资助项目(2015AA043001)；高等学校博士学科点专项科研基金优先发展领域资助项目(20120181130012)

*收稿日期：2015-02-24

文章编号：1674-2974(2016)02-0056-08