路的积图的无圈染色

董新芳，田双亮，刘睿琳

(西北民族大学 数学与计算科学学院，甘肃 兰州 730030)

路的积图的无圈染色

董新芳，田双亮*，刘睿琳

(西北民族大学 数学与计算科学学院，甘肃 兰州 730030)

研究路的两类积图直积与半强积的无圈染色，并给出了两个路的直积和半强积的无圈染色数.

路；无圈染色；直积图；半强积图；无圈染色

0 引言

设G是具有顶点集V(G)与边集E(G)的简单连通图,并用Δ(G)表示G的最大度.1973年Grünbaum在文献[1]中提出了无圈染色概念.图的无圈染色是指图G中不含有2-色圈的正常点染色，所用最少的颜色数记为a(G)，并提出了关于平面图无圈染色的猜想：每个平面图都是无圈5-可染的.1979年，Borodin在文献[2]中证明了这个猜想，同时还证明了在这个上界是可达的.1991年，Alon对一般图类无圈染色数的上界进行了深入研究，利用贪心算法证明了任意图G，有a(G)≤Δ2(G)+1[3].Gerke等人在无圈染色基础上，于2002年在文献中提出了更一般的无圈染色概念——广义无圈染色[4]，并给出了最大度为d的图的广义无圈染色数的上界.更多有关无圈染色的结果详见文献[5-8].

根据无圈染色定义，显然有以下两个引理：

引理1.1 对G的任意子图H，有a(H)≤a(G).

引理1.2 设图G有1个连通分支G1，G2，…，G1，则a(G)=max{a(Gi)|i=1,2,…，1}.

关于图的直积与半强积的概念具体如下：

定义1.1[4]G和H的直积是指具有顶点集V(G)×V(H)的图G∧H，其中(u,v)与(u＇,v＇)相邻当且仅当uu＇∈E(G)且vv＇∈E(H)．

由图的直积定义，显然，Δ(G∧H)=Δ(G)·Δ(H)，G∧H≌H∧G.

定义1.2[4]G和H的半强积是指具有顶点集V(G)×V(H)的图G·H，其中(u,v)与(u＇,v＇)相邻当且仅当或者uu＇∈E(G)且vv＇∈E(H)，或者u=u＇且vv＇∈E(H)．

由图的半强积定义，显然，

Δ(G·H)=Δ(G)·Δ(H)+Δ(H)，G·H=(G∧H)∪(N∧H),

其中N∧H表示N与H的笛卡尔积，N是具有顶点集V(G)的空图.

本文主要研究两个路的直积与半强积的无圈点染色.为简化表示，文中用(z)k表示zmodk，其中z为整数，k为正整数，并用Vc表示图中染颜色c的顶点集合.文中未说明的术语和符号见文献[9].

1 主要结论及其证明

设Pm与Pn分别为m阶和n阶的路，其中m,n≥2，并设Pm与Pn的顶点集分别为V(Pm)={0,1,…，m-1},V(Pn)={0,1,…，n-1}.

为研究两个路的直积的无圈染色，首先给出以下引理：

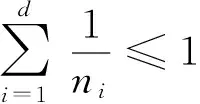
由引理2.1知，2-维网格的无圈染色数不超过3.关于路的直积的无圈染色，有以下结果：

定理2.1 设n≥m≥2.若m=2，则a(Pm∧Pn)=2，否则，a(Pm∧Pn)=3.

证明 当m=2时，因Pm∧Pn是由两条不相交的路构成，所以a(Pm∧Pn)=2.

当m≥3时，因Pm∧Pn的连通分支均为2-维网格的子图，由引理1.1、引理1.2与引理2.1知，a(Pm∧Pn)≤3. 又因当m,n≥3时，Pm∧Pn中至少有一个4阶圈，所以a(Pm∧Pn)>2.因此,a(Pm∧Pn)=3.

关于路的半强积的无圈染色有以下结果：

定理1.2 若m=2且n=3,或n=2，则a(Pm·Pn) =3，否则，a(Pm·Pn) =4.

证明 分以下两种情况讨论：

情况1m=2且n=3，或n=2.当m=2且n=3时，因P2·Pn中含有4-阶圈，所以a(P2·P3)≥3，因此仅需给出P2·P3的3-无圈染色. 令

σ(0,0)=σ(2,0)=σ(0,1)=σ(2,1)=0,σ(1, 0)=1,σ(1,1)=2.

容易验证，σ是P2·P3的3-无圈染色.

当n=2时，因Pm·P2中含有4-阶圈，所以a(Pm·P2)≥3，因此仅需给出Pm·P2的一个3-无圈染色.

对x=0,1,y=0,1,…，m-1，令σ(0,y)=0，σ(1,y)=1+(y)2.显然，σ所用颜色数为3.

首先，证明σ是Pm·P2的正常染色. 对Pm·P2的任意点(x,y)，其中x=0,1,y=0,1,…，m-1，根据σ的定义，σ(0,y)=0，且顶点(0,y)的3个可能邻点所染颜色为

σ(1,y+1)=1+(y+1)2,σ(1,y)=1+(y)2,σ(1,y-1)=1+(y-1)2.

显然，(0,y)的颜色与其邻点的颜色不同. 类似地，σ(1,y)=1+(y)2，且顶点(1,y)的3个可能邻点的颜色为σ(0,y+1)=σ(0,y)=σ(0,y-1)=0.显然(1,y)的颜色与其邻点的颜色不相同.由以上分析知，σ是Pm·P2的正常染色.

其次，说明σ是无圈的. 因染{0,1,2}中任意两种颜色的顶点在Pm·P2中的导出子图要么是路，要么为空图，所以σ是无圈的.

综上所述，σ是Pm·P2的3-无圈染色，因此a(Pm·P2)=3.

情况2m=2且n≥4，或m,n≥3. 考虑以下两种子情况：

情况2.1m=2且n≥4时，可以证明a(P2·Pn)>3. 事实上，假设a(P2·Pn)≤3. 取σ是P2·Pn的3-无圈染色，所用颜色集合为{a,b,c}，则对1≤x≤n-2，有σ(x,0)≠σ(x,1). 否则，存在1≤x0≤n-2，使得σ(x0,0)=σ(x0,1).不妨设σ(x0,0)=a，因σ是无圈染色,所以顶点(x0-1,0)与(x0-1,1)染不同的颜色.不妨设σ(x0-1,0)=b,σ(x0-1,1)=c，则σ(x0+1,1)=b或c. 此时形成颜色a,b的2-色圈或颜色a,c的2-色圈， 这与σ是无圈的推论相矛盾.

在P2·Pn中，因n≥4， 所以有σ(1,0)≠σ(1,1),σ(2,0)≠σ(2,1),而σ(1,0)∉{σ(2,0),σ(2,1)},σ(1,1)∉{σ(2,0),σ(2,1)}，所以4个顶点(1,0)、(2,0)、(1,1)、(2,1)在σ下染不同的颜色，即所需颜色数至少为4. 这与σ是3-无圈染色矛盾. 因此，a(P2·Pn) ≥4.

现在证明a(P2·Pn) ≤4，即需给出P2·Pn的一个4-无圈染色. 对x=0,1,…,n-1,y=0,1,令a(x,y)=(2x+y)4.显然，σ所用颜色数为4.

对P2·Pn的任意点(x,y)，其中x=0,1,…，n-1,y=0,1,根据σ的定义，σ(x,0)=(2x)4，且顶点(x,0)的4个可能邻点所染颜色为σ(x-1,0) =σ(x+1,0)=(2x+2)4,σ(x-1,1)=σ(x+1,1)=(2x+3)4.

显然，(x,0)的颜色与其邻点的颜色不同. 类似地，σ(x,1)=(2x+1)4,且顶点(x,1)的4个可能邻点的颜色分别为σ(x-1,1)=σ(x+1,1)=(2x+3)4,σ(x-1,0)=σ(x+1,0)=(2x+2)4.

显然(x,1)的颜色与其邻点的颜色不相同.由以上分析知，σ是Pm·P2的正常染色.

注意到，V0∪V2,V1∪V3,V0∪V3,V1∪V2分别在P2·Pn中的导出子图均为路，V2∪V3，V0∪V1分别在P2·Pn中的导出子图均为空图.因此，σ是无圈的.

由以上分析可知，σ是P2·Pn的4-无圈点染色.

情况2.2m,n≥3，则a(Pm·Pn)>3. 否则，假设a(Pm·Pn)≤3，令σ为Pm·Pn是3-无圈点染色. 由情况2.1中讨论知，σ(1,0)≠σ(1,1)，σ(1,1)≠σ(1,2)，显然σ(1,0)≠σ(1,2).否则，σ(0,1) ∉{σ(0,1),σ(1,1),σ(1,2)}.不失一般性，假设颜色集合为{a,b,c}，且σ(1,0)=σ(1,2)=a,σ(1,1)=b，则σ(0,1)=σ(2,1)=c.此时Pm·Pn中包含顶点为(1,0)、(2,1)、 (1,2)、(0,1)的一个2-色圈，这与σ是无圈相矛盾的. 因此，a(Pm·Pn)>3.

欲证a(Pm·Pn)≤4，仅需给出Pm·Pn的一个4-无圈点染色. 对0≤x≤n-1，0≤y≤m-1，令σ(x,y)=(2x+y)4.显然，σ所用颜色数为4.

首先证明σ是Pm·Pn的正常点染色.对于任意顶点(x,y) ∈V(Pm·Pn)，其所有可能的邻点共有6个，它们所染颜色分别为

σ(x,y)=(2x+y)4,

σ(x+1,y+1)=(2x+y+3)4,σ(x+1,y)=(2x+y+2)4,

σ(x+1,y-1)=(2x+y+1)4,σ(x-1,y-1)=(2x+y-3)4,

σ(x-1,y)=(2x+y-2)4,σ(x-1,y+1)=(2x+y-1)4.

容易验证(x,y)的颜色与其所有可能邻点的颜色不同，所以σ是Pm·Pn的正常点染色.

现在证明σ是无圈的.为讨论方便，不妨假设m,n充分大.任取两种不同颜色c1,c2∈{0,1,2,3}.并设顶点u={x,y}与v=(x＇，y＇)分别染颜色c1,c2.不妨设x＇>x，此时，x＇=x+1,y＇=y，或x＇=x+1且y＇=y+1或x＇=x+1且y＇=y-1.

当x＇=x+1，y＇=y时，根据σ的定义，则v的不同于u的5个邻点中，仅有顶点v1=(x+2,y)染颜色c1，在u的不同于v的5个顶点中，仅有u1=(x-1,y)染颜色c2.重复以上过程，染颜色c1与c2的顶点形成了一条路(见图1(1))，所以Vc1∪Vc2在Pm·Pn中的导出子图是无圈的.

当x＇=x+1,y＇=y+1,时，根据σ的定义，则v的不同于u的5个邻点中，仅有顶点v1=(x+2,y)染颜色c1.在u的不同于v的5个顶点中，仅有u1=(x-1,y+1)染颜色c2.重复以上过程，染颜色c1与c2的顶点形成了一条路(见图1(2))，所以Vc1∪Vc2在Pm·Pn中的导出子图是无圈的.

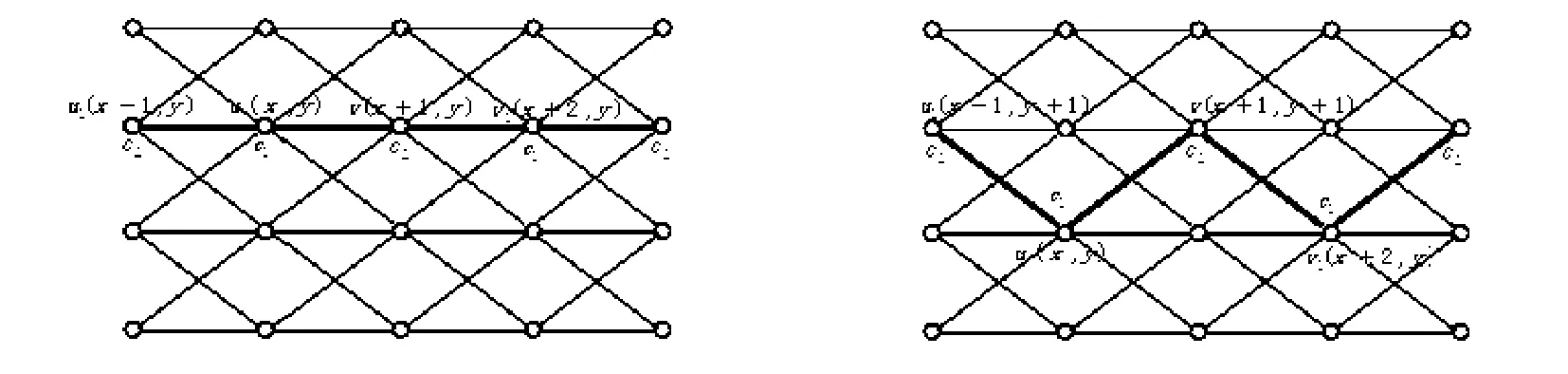
(1)x＇=x+1,y＇=y(2)x＇=x+1,y＇=y+1

图1Vc1∪Vc2在Pm·Pn中的导出子图(粗线部分)

类似地，当x＇=x+1且y＇=y-1时，根据σ的定义，则v的不同于u的5个邻点中，仅有顶点v1=(x+2,y)染颜色c1.在u的不同于v的5个顶点中，仅有u1=(x-1,y-1)染颜色c2，重复以上过程，染颜色c1与c2的顶点形成了类似于图1(2)的一条路，所以Vc1∪Vc2在Pm·Pn中的导出子图是无圈的.

由以上分析知，σ是无圈的，因此σ是Pm·Pn的4-无圈点染色.

[1]GrünbaumB.Acycliccoloringsofplanargraphs[J].IsraelJournalofmathematics, 1973, 14: 390-408.

[2]BorodinOV.Onacycliccoloringsofplanargraphs[J].DiscreteMathematics，1979,25: 211-236.

[3]AlonN,McDiarmidC,ReedB.Acycliccolouringofgraphs[J].RandomStructuresAlgorithms,1991, 2(3): 277-288.

[4]GreenhillC,PikhurkoO.Boundsonthegeneralizedacyclicchromaticnumbersofbounddegreegraphs[J].GraphsandConbinatorics,2005,21:407-419.

[5]FertinG,GodardE,RaspaudA.Acyclicandk-distancecoloringofthegrid[J].InformationProcessingLetters, 2003, 87:51-58.

[6]FiamcikǐI.Theacyclicchromaticclassofagraph[J].Math.Slovac,1978, 28: 139-145.

[7]SkulrattanakulchaiS.Acycliccoloringsofsubcubicgraphs[J].InformationProcessingLetters, 2004,92: 161-167.

[8]LyonsA．Acyclicandstarcoloringsofcographs[J]．DiscreteAppliedMathematics, 2011, 159: 1842-1850．

[9]BondyJA,MurtyUSR.GraphtheorywithApplications[M].NewYork:theMacmillanpressLtd, 1976.

Product Graphs Acyclic Coloring of Path

DONG Xin-fang, TIAN Shuang-liang, LIU Rui-lin

(Mathematics and Computer Science College，Northwest University for Nationalities，Lanzhou 730030, China)

In this paper, we studied the simple graph of the direct product graph and semi strong product acyclic coloring and minimum chromatic number (markeda(G)). Using graph decomposition, construct dyeing method, given with path and path, path and cycle direct product of graphs and semi strong product graphs of acyclic chromatic number.

Acyclic coloring; Direct product graphs; Semi strong product graphs

2016-11-10

国家民委科研项目(14XBZ018)；甘肃省自然科学基金(145RJZA158)；西北民族大学中央高校基本科研业务费专项资金资助研究生项目(Yxm2015180、Yxm2015182)；西北民族大学中央高校基本科研业务费专项资金项目(31920160064).

*

董新芳(1986—)，女，甘肃兰州人，硕士研究生，主要从事组合数学与图论方面的研究.

O157.5

A

1009-2102(2016)04-0001-04