置换对称性在多元函数积分中的应用
2016-04-23张元婷
张元婷
(安徽科技学院 信息与网络工程学院,安徽 凤阳 233100)
置换对称性在多元函数积分中的应用
张元婷
(安徽科技学院信息与网络工程学院,安徽凤阳233100)
摘要:本文研究置换对称性成立的条件,由此给出了二重积分、三重积分、曲线积分和曲面积分的置换对称性定理,并给出利用置换对称性简化问题的若干实例。
关键词:置换对称性;轮换对称性;对换;多元函数
积分学是高等数学的重要组成部分,其内容丰富,应用广泛,巧用几何意义和物理意义[1]以及对称性计算积分可大大的简化计算,提高计算效率。在定积分的计算中,巧妙地利用积分区域关于原点的对称性和被积函数的奇偶性,可达到事半功倍的效果,此命题在经过推广后,利用积分区域关于坐标轴、坐标面的对称性和被积函数的奇偶性,可简化二重积分、三重积分、曲线积分和曲面积分的计算[2-4]。随后,考虑到定积分仅与积分域及被积函数的对应法则有关,而与积分变量的符号无关,借助轮换对称性的定义,部分教育工作者利用积分区域关于变量的轮换对称性研究积分的计算[5-7]。鉴于此,本文受已有文献的启发,引入抽象代数中的置换概念,定义了积分域的置换对称性,探讨在置换对称性下多元函数的积分,给出各种积分的计算公式,用这些公式可转化被积函数的结构,使积分计算简便易行。
1预备知识
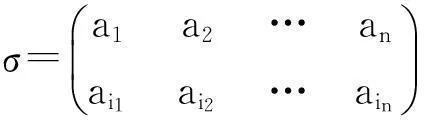
注:本文所指的置换均指非恒等置换。
定义1.2[8]若σ是一个n次置换,满足(1)σ(a1)=a2,σ(a2)=a3,…,σ(a1)=a1;(2)σ(a)=a,当a≠ai(i=1,2,…,l),则称σ是一个长为l的轮换,并记作σ=(a1,a2,…,al),长度为2的轮换称为对换。

若有限集合A={x,y,z},则可能的置换为:

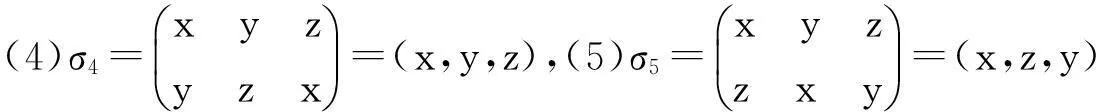
其中σ1,σ2,σ3是2-轮换(对换),σ4,σ5是3-轮换。 下文不加说明的话,σi(1≤i≤5)均为此置换。
定义1.3若Ω表示一个与方向无关有界几何体(曲线段、平面区域、空间区域、曲面块等),若σ是关于变量的一个置换,满足σ(Ω)=Ω,即经过置换后边界方程不变,则称Ω关于该置换具有置换对称性。
2积分域无方向的多元函数置换对称性定理
由文献[9]可得,当点M(x1,x2…xn)∈Rn时,数量值函数为f(M)=f(x1,x2,…,xn),其中x1,x2,…xn称为函数f的自变量,域Ω表示一个有界的几何体(曲线段、平面区域、空间区域、曲面块等),此时数量值函数在域上的积分可表示为∫Ωf(x1,x2,…xn)dΩ。
引理2.1[9]若T:y1=y1(X),y2=y2(X),…,yn=yn(X)为可逆变换,Ω为有界闭区域,f(y1,y2,…,yn) 是T(Ω)上的连续函数,则有n重积分的变量代换公式:
其中X=(x1,x2,…,xn).
定理2.1设Ω表示一个与方向无关有界几何体,多元函数f(x1,x2,…,xn)在域Ω上可积,若存在一个置换σ,满足σ(Ω)=Ω,则有
∫Ωf(x1,x2,…,xn)dΩ=∫Ωσ(f(x1,x2,…,xn))dΩ

∫Ωσ(f(x1,x2,…,xn))dΩ
=∫Ωσ(f(x1,x2,…,xn))dx1dx2…dxn
=∫σ(Ω)σ(f(x2,x2,…,xn))dx1dx2…dxn
=∫σ(Ω)f(σ(x1),σ(x2),…,σ(xn))dx1dx2…dxn
=∫Ωf(x1,x2,…,xn)dx1dx2…dxn
=∫Ωf(x1,x2,…,xn)dΩ
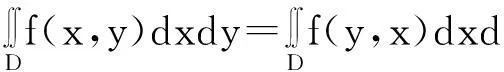
推论2.2若二元函数在平面曲线弧上可积,且对置换σ=(x,y),满足σ(L)=L,即曲线弧关于直线y=x对称,则∫Lf(x,y)ds=∫Lf(y,x)ds.
推论2.3若三元函数f(x,y,z)在空间曲线Γ上可积,则有:
(1)若σ1(Γ)=Γ,则∫Γf(x,y,z)ds=∫Γf(y,x,z)ds.
(2)若σ2(Γ)=Γ,则∫Γf(x,y,z)ds=∫Γf(z,y,x)ds..
(3)若σ3(Γ)=Γ,则∫Γf(x,y,z)ds=∫Γf(x,z,y)ds.
(4)若σ4(Γ)=Γ,则∫Γf(x,y,z)ds=∫Γf(y,z,x)ds..
(5)若σ5(Γ)=Γ,则∫Γf(x,y,z)ds=∫Γf(z,x,y)ds.
推论2.4若三元函数f(x,y,z)在空间有界闭区域Ω上可积,则有:
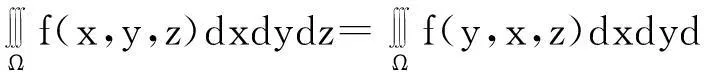
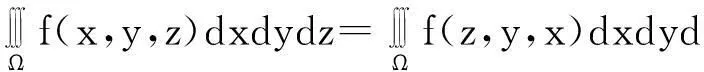
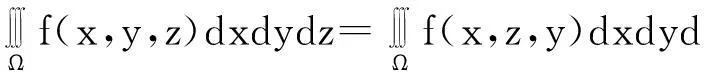
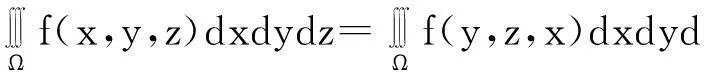
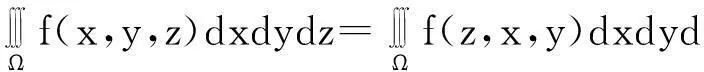
推论2.5若三元函数f(x,y,z)在空间曲面∑上可积,则有
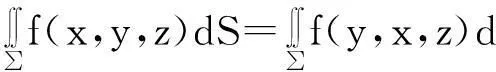
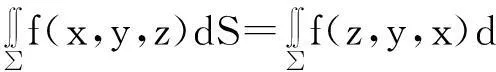
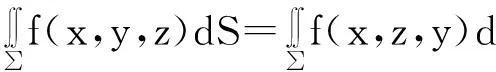

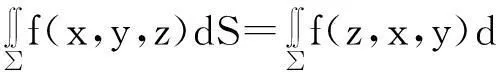
3积分域有方向的多元函数置换对称性定理
由于置换不能保方向性,下面浅谈下积分域有方向时的置换对称性。
若L为有向曲线弧,若不考虑方向性,L经过置换σ=(x,y)后曲线方程不变,即任一点(x,y)∈L,有(y,x)∈L。从而平面曲线L关于直线y=x对称,则曲线L经过置换σ后,曲线L关于直线y=x翻转,其方向刚好与原方向相反,即曲线L经过置换σ后是L-(L的反向曲线弧)。
定理3.1若P(x,y)和Q(x,y)均在有向曲线弧L上连续,且对置换σ=(x,y),满足σ(L)=L-,则有∫LP(x,y)dx+Q(x,y)dy=-∫LP(y,x)dy+Q(y,x)dx.
证明:
∫LP(x,y)dx+Q(x,y)dy=∫σ(L)σ(P)dσ(x)+σ(Q)dσ(y)
=∫L-P(y,x)dy+Q(y,x)dx
=-∫LP(y,x)dy+Q(y,x)dx
(1)若积分曲面∑经过σ1置换后曲面方程不变,即曲面关于平面y=x对称,且曲面的法向量方向不变,则有:

(2)若积分曲面∑经过σ2置换后曲面方程不变,且曲面的法向量方向不变,则有:

(3)若积分曲面∑经过σ3置换后曲面方程不变,且曲面的法向量方向不变,则有:

(4)若积分曲面∑经过σ4置换后曲面方程不变,且曲面的法向量方向不变,则有:

(5)若积分曲面∑经过σ5置换后曲面方程不变,且曲面的法向量方向不变,则有:

4应用举例

从而有
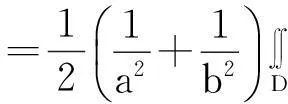
在极坐标中,积分区域D={(θ,ρ)|0≤θ≤2π,0≤ρ≤R},于是有
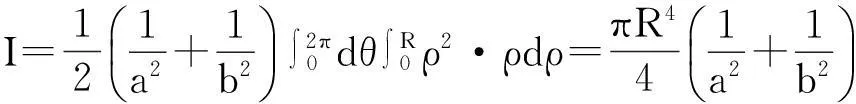
解:利用Ω的对称性,分别对换x,y和z,有

于是
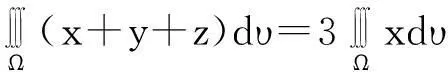
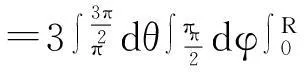

例3设平面曲线L为圆周x2+y2=1,求∫Lx2ds.
解:利用L的对称性,对换x,y,有∫Lx2ds=∫Ly2ds,
从而有

解:利用积分曲面∑的对称性,分别对换x,y和x,z,有
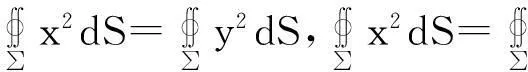
于是
证明:(1)利用积分区域的对称性,对换x,y,于是有
于是

解:利用球面的对称性,分别对换x,z和y,z,于是有

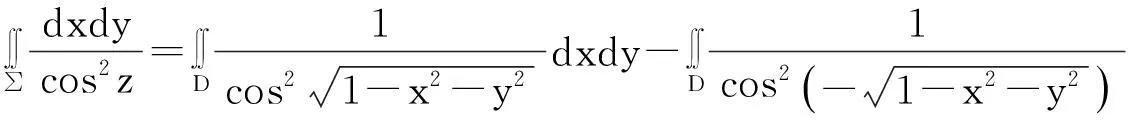
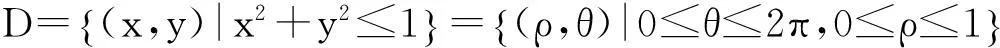
从而
=4πtan1.
参考文献:
[1]丁峰.利用几何意义和物理意义巧解积分[J].安徽科技学院学报, 2007,21(1):50-52.
[2]曹斌,孙艳.对称性在积分计算中的应用[J].吉林师范大学学报:自然科学版,2012,33(3):125-128.
[3]郑妤.利用对称性简化第二类曲面积分[J].高等数学研究,2014,17(2):42-43.
[4]周海青.对称性在曲面积分计算中的应用[J].青海大学学报:自然科学版,2002,20(6):55-57.
[5]马军英.用积分域变量轮换对称性计算几类积分[J].山东师范大学学报:自然科学版,2004,19(1):79-81.
[6]李源,郝小枝.多元数量值函数积分中的轮换对称性[J].云南大学学报:自然科学版,2013,35(S2):433-437.
[7]王建平,张香伟.积分的轮换不变性在重积分计算中的应用[J].河南教育学院学报:自然科学版,2014,23(2):13-15.
[8]胡冠章,王殿军.应用近世代数(第3版)[M].北京:清华大学出版社,2006.
[9]陈纪修,於崇华,金路.数学分析(第2版)[M].北京:高等教育出版社,2004.
[10]同济大学数学系.高等数学(第6版)[M].北京:高等教育出版社,2007.
(责任编辑:马世堂)
Application of the Permutation Symmetry in Multivariate Function Integral
ZHANG Yuan-ting
(College of Information and Network Engineering, Anhui Science and Technology University, Fengyang 233100,China)
Abstract:In this paper, the conditions for the permutation symmetry are discussed, and according to it, permutation symmetry theorem is given in double integral, triple integral, curve integral and surface integral. Some examples about application theorem to simplify the problem are given.
Key words:Permutation symmetry;Rotation symmetry;Exchange;Multivariate function.
中图分类号:O13
文献标识码:A
文章编号:1673-8772(2016)01-0103-06
作者简介:张元婷(1987-),女,安徽省六安市人,硕士,助教,主要从事代数编码与密码研究。
基金项目:安徽省振兴计划项目(2014zdjy098)。
收稿日期:2015-10-26
