基于朴素贝叶斯的航空反潜搜索辅助决策模型

秦瑞祥,冯　策

(1.海军驻北京地区航空军代表室，北京　100041；

2.中国电子科学研究院，北京　100041)

秦瑞祥(1963—)，男，河北正定人，高级工程师，主要研究方向为任务规划系统及自动控制技术等；

E-mail：hjqrx19@163.com

冯　策(1984—)，男，黑龙江牡丹江人，工程师，主要研究方向为分布式仿真系统，虚拟现实。



工程与应用

基于朴素贝叶斯的航空反潜搜索辅助决策模型

秦瑞祥1，2,冯策2

(1.海军驻北京地区航空军代表室，北京100041；

2.中国电子科学研究院，北京100041)

摘要：在分析现代航空反潜搜潜决策过程的基础上，针对航空反潜中的辅助决策问题，提出了基于朴素贝叶斯的辅助决策模型，首先利用条件互信息最大化的特征选择算法筛选出满足假设条件的有效特征，然后采用朴素贝叶斯分类器构建反潜作战指挥辅助决策模型，最后设计了仿真用例，对辅助决策模型进行了验证。仿真结果表明基于朴素贝叶斯的辅助决策模型所计算出的搜索组合方案，符合反潜巡逻机的典型搜索方式。

关键词：搜潜；航空反潜；辅助决策；朴素贝叶斯

0引言

快速准确地发现潜艇目标是进行战场态势评估和战场决策的基础，但是由于战场中存在的大量信息和不确定因素，以及潜艇向低噪和高速方向发展，使搜潜更为困难。因此，如何能够根据不同的状况采取正确的搜潜策略是航空反潜中首要解决的问题。

反潜巡逻机通常在通过其他兵力获取预知信息后，再通过多种搜潜手段组合的方式对指定的海域做进一步的探测。搜潜过程中的探测手段有雷达、声呐浮标、磁探仪、红外探测仪等设备，指挥人员需要根据预知信息以及各种手段的特点，及时给出合理的搜潜方案，但是战场中多维信息的不确定性给指挥人员的快速决策带来了极大的困难，例如目标的不确定性，环境的不确定性等等，仅仅依靠指挥人员的个人水平很难在短时间内给出合理的搜潜方案，因此，构建理想的搜潜辅助决策系统是现代反潜中一项重要的任务，理想的航空搜潜辅助决策系统会提供给指挥员以最优的搜索策略，弥补指挥员的经验不足所导致的低效能。

随着决策理论的发展，现代辅助决策模型目前在军事领域上得到了广泛的应用，主要以海上实体以及指挥作战平台为主，文献[1]提出了水面舰艇反潜决策系统。文献[2]提出了多属性决策理论方法。文献[3]研究了模糊综合评估的指挥控制效能评估模型。文献[4]提出了结合神经网络和模糊理论在潜艇指挥中的应用。文献[5]通过建立反潜直升机搜潜效能数学模型，给出了不同预设搜潜模式下的典型武器挂载方案的辅助决策系统。文献[6]分析了现代反潜巡逻机不同搜索手段的特点与指挥员决策基本过程，明确了运用现代决策方法建立搜潜方案的辅助决策系统的研究重点和方向。

综合分析航空搜潜中所存在的特点，本文采用朴素贝叶斯分类器建立起综合考虑探测信息，搜索能力，成本，隐蔽性和实施难度等多方面因素的辅助决策模型。

1搜索方案估计

由于与海上战场环境和潜艇目标出现状态的不确定性，以及搜索攻击手段的特点不同，使得各种搜索和供给方案的优劣往往难以精确的描述，而只能用模糊的、难以明确的模型来描述。

针对反潜任务中所存在的不确定性问题，本文采用朴素贝叶斯分类器构建决策模型，这是由于朴素贝叶斯具有以下优势：

(1)能够方便地处理不确定信息，同时适用于处理多类别问题，例如多种探测手段组合方案的决策;

(2)模型所需估计的参数很少，对缺失数据不太敏感，在数据较少的情况下仍然有效;

(3)算法相对简单，并行化容易，实时性较好，能及时反馈给指挥人员以合适的搜潜方案。

贝叶斯的分类模型综合巡逻机机上多维传感器信息与战场上观测收集到的信息进行判断，将定性判断与定量计算相结合来描述目标特征，从信息论的角度来看该模型是合理且完备的。

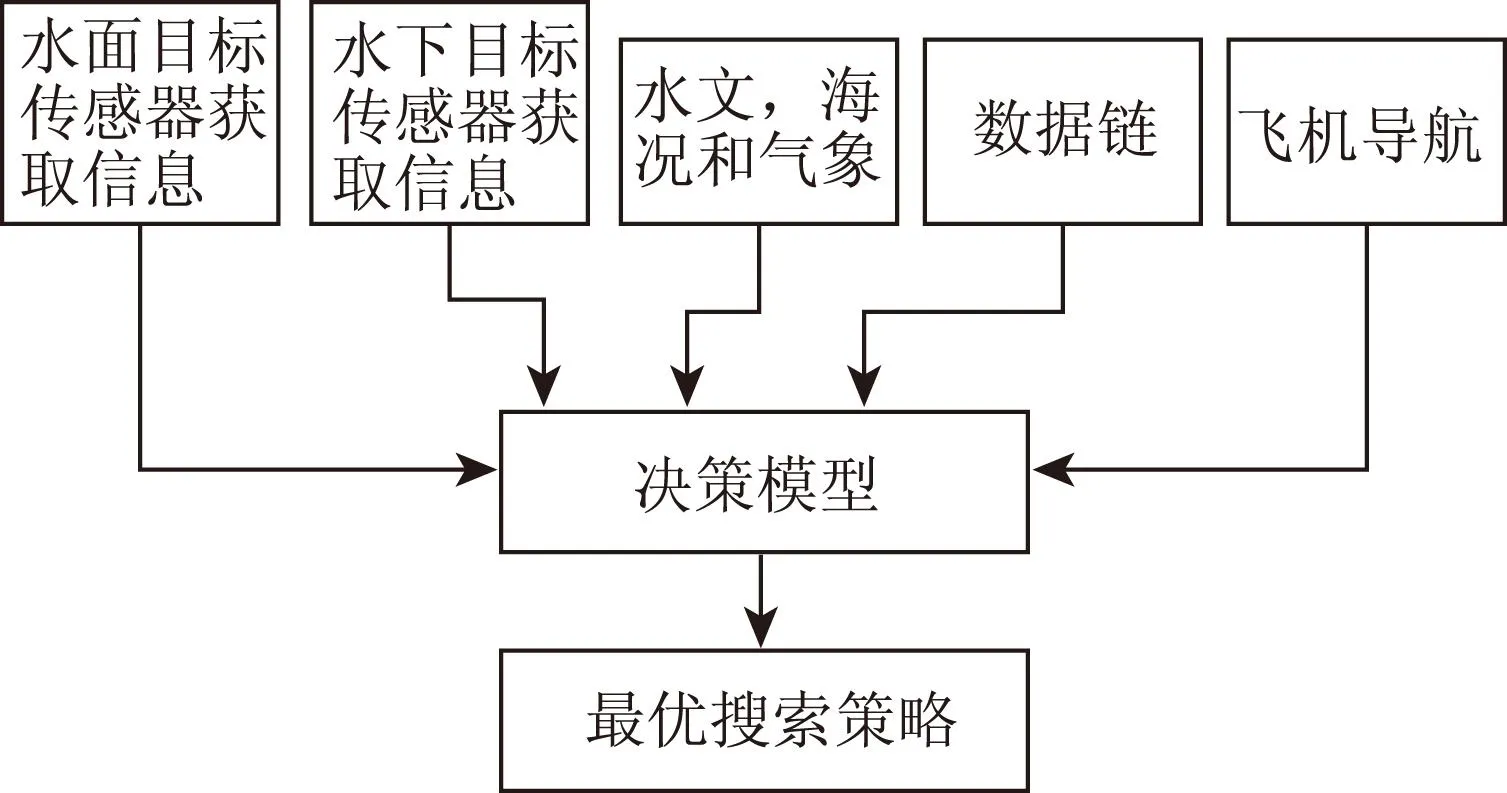
图1　搜潜辅助决策结构图

组合搜索方案的输入信息来源于多维信息，例如水面目标传感器获取的信息，水下目标传感器获取的信息，水文，海况和气象等等，然后从这些信息中选取最为有代表性的特征，构建特征集合，用fn(n=1,2,…N)来表示，最后利用朴素贝叶斯模型来构建特征分类器。

反潜巡逻飞机通常使用声呐浮标(S)、磁探仪(M)、搜索雷达(R)、红外搜索仪(I)，和电子支援系统(E)等搜索设备进行搜索，可以组合成31种不同方案。针对不同状态，采用不同的搜潜行动方案，搜索方案用C={C1,C2,C3,C4,C5,C6}表示。剔除不合理的方案，得到一组方案子集：

其中六种组合分别为：

搜索方案C为决策模型的方案库，因此6组方案对应着朴素贝叶斯模型输出的6个类别，用Ci∈C(i=1,2,3,4,5,6)表示。

2决策模型描述

引入贝叶斯分类模型，通过特征属性fn(n=1,2,…N)确定最优的方案，如式(1)所示：

(1)

上式由贝叶斯公式求得:

(2)

假定先验概率P(C=Ci)为均匀分布。而其中分母部分不包含类别变量，因此只要求得P(f1,f2,f3,…,fN|C=Ci)即可得到最优输出，简化为：

(3)

朴素贝叶斯概率假设条件是特征属性之间是相互独立的，特征属性之间的独立意味着每个特征的分布都可以独立地被作为一维分布来估计，这样降低了由于维灾难所带来的困难。因此，根据其特征独立的假设条件，式(3)可转换为：

(4)

朴素贝叶斯模型优点是模型所需估计的参数很少，在理论上与其他分类方法相比具有最小的误差率。但是由于其假设条件是属性之间相互独立，这个假设在实际应用中往往是不成立的，这给朴素贝叶斯模型的正确分类带来了一定影响。因此如何选取有效的，且相互独立特征属性是本文首先要解决的问题。

2.1特征提取

本文采用条件互信息最大化[8]的特征选择算法来进行特征的筛选，互信息通常用于计算特征与特征之互信息最大化的关系，特征选择在于选取对训练数据具有分类能力的特征。所谓条件互信息最大化，就是选择有效特征，满足分类模型特征独立的假设，保留关于类别的信息，减少预测的不确定性。

特征选择方法的基本思想是从原特征集合{f1,f2,f3,…,fN}中选择一个有效特征子集构成一个新的特征空间，使得条件熵H(C|f1,…,fK)最小。本文Ci(i=1,2,3,4,5,6)有6个类别，因此条件熵如下：

(5)

基于条件互信息最大化特征选择算法，使用单个特征来代替特征子集。此算法可筛选出属性独立的有效特征，满足朴素贝叶斯分类思想中假设条件，条件互信息如下：

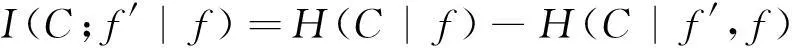
(6)

其中，f′为待检测特征，f为新选择的特征，H(C|f)是用来表示在已知f时C的经验条件熵，H(C|f′,f)是用来表示已知f′和f时C的经验条件熵，I(C;f′|f)表示已知特征f的条件下的f′与C的互信息。

具体思路是将待检测的特征f′与已选择的特征f进行比较，如果I(C;f′|f)值很小，则表示两种可能：

(1)f′与f中所包含C的信息很相似；

(2)f′中不包含C的信息。

如果I(C;f′|f)值很大，则表示两种可能：

“是，师父。”他的心里纵然满是疑惑，却也不敢再向师父追问什么。他站起身，躬身倒退数步，而后转身离开了望天归。

(1)f中含有表示C的信息；

(2)f′与f中所包含C的信息不同

可见，I(C;f′|f)值很大时满足了朴素贝叶斯模型的特征独立假设条件，特征属性之间是相互独立的，而此特征同时具备表示该类别的能力。具体表示如下：

(7)

(8)

算法目标是选择I(C;fn|fl)较大的fn构建特征空间，从而确保朴素贝叶斯分类的可准确性。

经过条件互信息最大化的特征选择算法筛选出的有效特征为探测范围、目标下潜深度、浮标数量、探测时间、隐蔽性、海洋与大气具体参数。

2.2拉普拉斯平滑

贝叶斯算法会出现由于零概率而导致的决策错误问题，因此本文采用拉普拉斯平滑方法来解决特征缺失所导致的零概率问题，所谓零概率问题，就是在计算新实例的概率时，如果某个特征在训练集中没出现过，就会导致整个实例的概率计算结果为0。在搜潜决策过程中，如果当某个信息特征在训练集中为空，例如潜艇潜航状态在训练集中没有出现过，为那么对最优方案Ci的条件概率P(fn|C=Ci)(n=1,2,…N)的估计结果为0。

条件概率P(fn|C=Ci)(n=1,2,…N)在fn=k时的后验概率如下：

(9)

其中，Nk,i为类Ci的训练样本中fn=k的样本数，分母部分为fn=k时类Ci的总样本数。为避免0概率的出现，引入拉普拉斯平滑，在随机变量的各个取值的频数上赋予一个正数λ=1，如下式所示：

(10)

3仿真结果与分析

为了验证算法的有效性，采用条件互信息最大化方法进行特征筛选，然后利用仿真数据样本进行朴素贝叶斯模型的训练，即可得到任意属性项的条件概率值，本文给出5种特征的后验概率：分别为潜艇目标位置，潜艇散布范围，以及探测时间，隐蔽性和携带浮标数量，分别如表1，表2和表3所示。

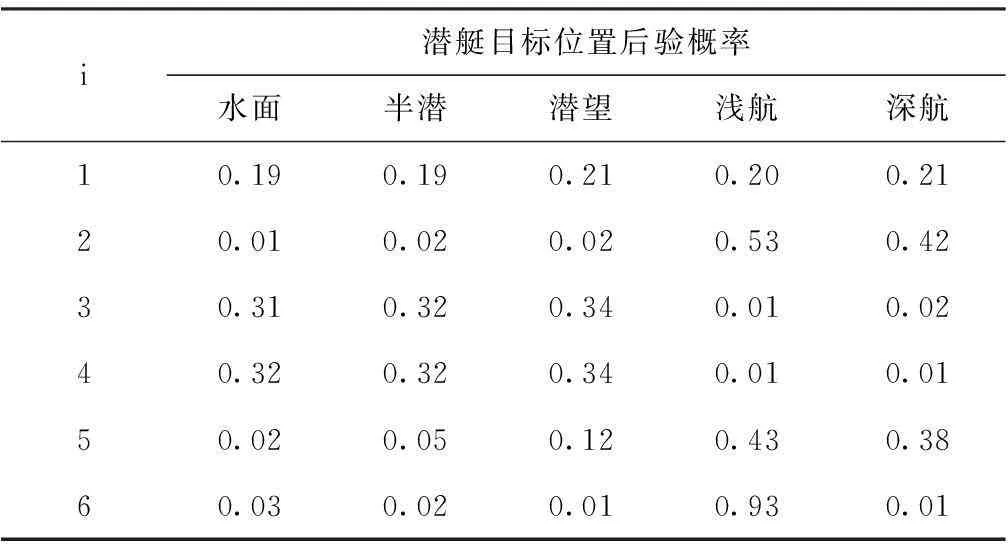
表1　潜艇目标位置后验概率

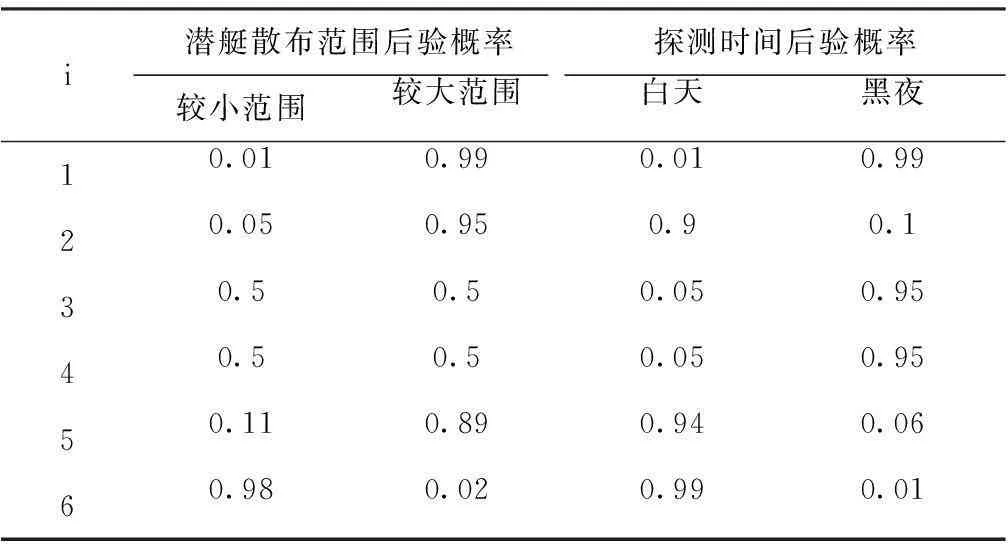
表2　散布范围和探测时间的后验概率

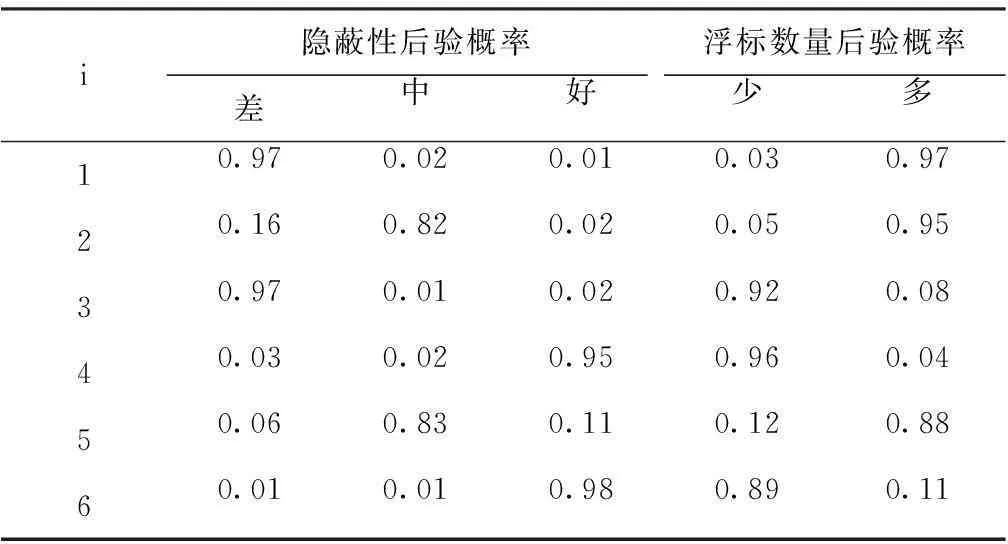
表3　隐蔽性和浮标数量的后验概率

本文选择6个特征属性进行计算：f1潜艇目标深度，f2潜艇散布范围，f3浮标数量，f4探测时间，f5隐蔽性，f6浮标数量，同时设计3个仿真用例来验证决策模型的有效性:

(1) 假设目标处于深度工作状态，声呐浮标数量充足，潜艇目标散布范围很广，在夜间飞行，隐蔽性较好。根据式(3)以及表1，表2，表3可得：

0.21*0.99*0.99*0.01*0.97=0.0019964637

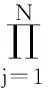
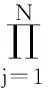
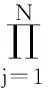
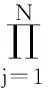
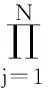
由结果比较可见当C=C1时，结果最大，因此通过朴素贝叶斯模型计算出最佳搜索方案为C1={R,I,E,S}，即推荐搜索雷达(R)、红外搜索仪(I)，和电子支援系统(E)，声呐浮标(S)多手段的组合搜索方式，在对水下目标搜索的同时，也同时对水面情况进行监控，及时捕获可能上浮的潜艇。

(2) 假设目标处于水面航行状态，声呐浮标数量充足，潜艇目标散布范围很小，在白天飞行，隐蔽性较好。同理通过朴素贝叶斯模型计算出最佳搜索方案为C3={R,I,E}，即推荐搜索雷达(R)、红外搜索仪(I)，和电子支援系统(E)组合手段来进行搜潜。

(3) 假设目标处于深度航行状态，声呐浮标数量较少，潜艇目标散布范围很小，在白天飞行，隐蔽性中等。同理通过朴素贝叶斯模型计算出最佳搜索方案为C6={M}，在声呐浮标数量不够充足的情况下，推荐只使用磁探仪来进行潜艇目标的搜索。

以上的计算结果与实际情况相符合，综上可见，本文提出的结合条件互信息最大化和朴素贝叶斯算法的搜潜决策模型所计算出的搜索方案，符合现代反潜战中反潜巡逻机的典型搜潜方式。

4结语

本文研究了基于朴素贝叶斯的航空反潜搜潜辅助决策模型，主要有以下两方面内容:

(1)采用条件互信息最大化特征选择算法，筛选出符合朴素贝叶斯假设的有效特征集合。

(2)采用朴素贝叶斯模型进行搜潜方案的辅助决策，综合多传感器与环境等信息特征进行搜潜方案的定性判断。

实验结果显示，在考虑反潜作战中的不确定性因素和以及环境的复杂性基础上，应用朴素贝叶斯决策模型于反潜战中，对于指挥人员的决策具有一定的辅助意义。为提升模型效率，下一步将尝试采用半朴素贝叶斯方法进行辅助决策模型的研究。

参考文献：

[1]郭锐, 余家祥. 现代水面舰艇反潜作战决策支持系统研究[J]. 舰船论证参考, 2004(1):1-3.

[2]魏世孝. 多属性决策理论方法及其在CI系统中的应用[M]. 国防工业出版社, 1998.

[3]蒋胜平, 孙华付, 汪清园. 基于二级综合模糊评判的指挥信息系统综合效能评估[J]. 舰船电子工程, 2012, 32(4):36-38.

[4]陆铭华，赵琳，潜艇指挥决策控制模型及其仿真[J]，船舶工程，2005,3.

[5]康乐. 反潜直升机武器挂载方案研究与仿真[J]. 中国电子科学研究院学报, 2014(1):70-74.

[6]屈也频, 廖瑛. 航空反潜搜索方案辅助决策系统研究

[J]. 电光与控制, 2008, 15(10):1-4.

[7]李航. 统计学习方法[M]. 清华大学出版社, 2012.

[8] Fleuret F. Binary feature selection with conditional mutual information[J]. 2003.

秦瑞祥(1963—)，男，河北正定人，高级工程师，主要研究方向为任务规划系统及自动控制技术等；

E-mail：hjqrx19@163.com

冯策(1984—)，男，黑龙江牡丹江人，工程师，主要研究方向为分布式仿真系统，虚拟现实。

Decision Support Algorithm Based on Naive Bayes for Search-scheme in Aviation Antisubmarine Warfare

QIN Rui-xiang1,2,FENG Ce2

(1. Naval aviation supervised delegate in Beijing，Beijing 100041，China；2. China Academy of Electronics and Information Technology，Beijing 100041，China)

Abstract:On the basis of analyzing the modern decision process of aviation antisubmarine submarine, we present the decision support model based on Naive Bayes to solve the decision support problem in aviation antisubmarine warfare. Firstly, we use Conditional Mutual Information Maximization algorithm to select the effective features to meet the assumptions, and then we establish the decision model based on Naive Bayes model. Finally, we design the simulation cases for testing decision support model. The simulation results show that the scheme calculated by searching submarine decision model is in accord with the typical scheme.

Key words:submarine search；aviation antisubmarine；decision support；Naive Bayes

作者简介

中图分类号：V271.4

文献标识码：A

文章编号：1673-5692(2016)01-084-04

收稿日期：2016-01-13

修订日期：2016-01-20

doi:10.3969/j.issn.1673-5692.2016.01.016