网栅参数对切割式多破片战斗部发散角的影响

赵长啸，张洋溢，路 亮，徐建国，赵东华，李惠明

（1.武汉军械士官学校，湖北 武汉，430075；2.广州军区工程科研设计所，广东 广州，510515；3.中国人民解放军72351部队，山东 莱芜，271109）



网栅参数对切割式多破片战斗部发散角的影响

赵长啸1，张洋溢2，路 亮3，徐建国1，赵东华1，李惠明1

（1.武汉军械士官学校，湖北 武汉，430075；2.广州军区工程科研设计所，广东 广州，510515；3.中国人民解放军72351部队，山东 莱芜，271109）

摘 要：为提高切割式多破片战斗部对目标的打击概率，在试验研究的基础上利用LS-DYNA仿真软件研究了切割网栅参数对战斗部发散角的影响。研究表明：随着切割丝安装距离的增加，破片发散角逐渐减小；相对于圆柱形，截面形状为楔形的切割丝切割效率更高，单位长度发散角变化值更小。

关键词：爆炸力学；多破片战斗部；发散角；模拟

切割式多破片战斗部装药[1-5]主要是通过切割处于变形过程中的药型罩，形成多个具有一定侵彻能力的破片式子弹丸，从而提高战斗部对目标的打击概率。Richard Fong等[1]首先设计了一种利用高强度金属杆切割药型罩形成破片式子弹丸的装药结构；张洋溢等[2]则对Richard Fong提出的装药结构成形过程进行了数值模拟研究及试验验证；李伟兵等[3]研究了切割金属杆排列形状对切割效果的影响；龙源等[4]则主要对环形起爆下起爆环半径对十字形切割式多破片战斗部成型参数的影响进行了研究，然而对于切割网栅参数对破片发散角的影响则未开展系统的研究。

十字形切割网栅因与药型罩接触面积小，故在切割过程中药型罩损失质量较少，生成破片动能大、侵彻能力强。因此，本研究以十字形切割式多破片战斗部为研究对象，重点对其成型规律及破片发散角随切割网栅参数变化规律进行研究，从而为进一步优化十字形切割式多破片战斗部装药结构，提高毁伤概率提供理论依据。

1　切割式多破片战斗部结构

十字形切割式多破片战斗部主要是对单个EFP装药的再设计，即在其药型罩前端设置一个十字形切割网栅，如图1所示。切割网栅由起固定作用的金属架和切割作用的钨杆组成，钨杆直径1.5mm，长度60mm；战斗部口径为60mm，高度为60mm；药型罩为弧锥结合罩，材料为紫铜罩，炸药为8701炸药，壳体材料为铝[5]。

图1　战斗部试验照片Fig.1 Picture of tested warhead

2　试验设置及结果分析

为了验证设计的切割式多破片战斗部结构的可行性和终点毁伤效应，对其进行了地面静爆试验。其中，在距战斗部20m、30m处分别布置一网靶以分析破片空间分布情况；在距离战斗部100m处，布置一钢靶，以检验战斗部的侵彻威力；靶板材料为45#钢，尺寸为2.2m×6m，厚度为6mm，靶板与地面保持垂直。图2为不同距离网靶上破片穿孔图。

图2　网靶破片穿孔图Fig.2 Picture of fragments perforation on net target

由图2可以看出战斗部起爆后，药型罩被切割丝切割并生产5枚破片。5枚破片分布较为均匀，呈现中心1枚周边4枚的均匀分布规律。同时由网靶上的穿孔分布可知，破片穿过第1道网靶时，破片分布相对集中，而穿过第2道网靶时，分布则相对发散，说明切割后形成的破片具有一定大小的径向速度，从而在飞行过程中产生了发散。

3　破片发散角影响因素分析

3.1发散角定义

由上述试验结果可知，切割药型罩形成的5枚破片由于存在一定的径向速度从而在飞行过程中产生发散，而发散角的大小将直接影响战斗部的打击范围，进而影响对目标的命中概率。图3为破片发散角示意图。

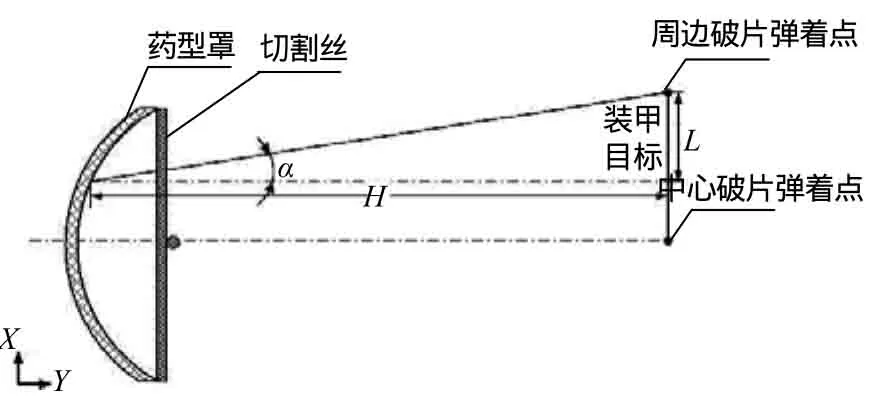
图3　破片发散角Fig.3 Radial dispersion angle of fragment

由图3 可得，破片发散角为：

式（1）中：α为破片发散角；L为周边破片的发散半径；H为破片到目标物之间的距离。

3.2数值模拟分析

由于采用传统试验方法获得破片发散角变化规律工作量大、耗费多，因此在已有试验数据的基础上，采用LS-DYNA数值模拟方法对破片发散角随网栅参数变化规律进行数值仿真研究。其中，数值计算模型采用1/2三维实体建模，如图4所示，模型尺寸按照战斗部实体尺寸，数值计算涉及的材料模型及计算参数详见文献[4]。

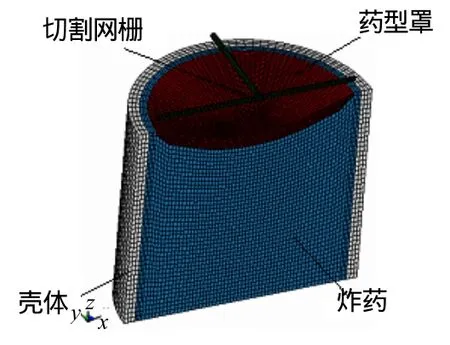
图4　1/2多破片战斗部计算模型图Fig.4 1/2 Numerical model of multiple fragments warhead

通过数值计算得到十字形切割式多破片战斗部成型的具体过程。炸药起爆后，药型罩在爆轰波作用下被压垮，此时，药型罩承受约400GPa的压力和接近金属熔点的温度，药型罩处于大塑性变形的流体状态。高速运动流体状态的药型罩与切割丝相碰撞并被切割成4部分。切割后的4部分药型罩继续翻转并向中间挤压直至径向速度为0。同时由于药型罩中心部位受到的爆轰能量大于周边部位，故中心部分轴向速度高于周边部分。因此，随着时间的推移，破片被逐渐拉长直至产生断裂。结果速度最快的药型罩中心部分运动在最前面，形成中心破片，而尾部部分则因径向速度的存在，分开成为4个具有相同的轴向速度和不同的径向速度的周边破片，如图5所示。

图5　数值计算结果Fig.5 The result of numerical calculation

由图2和图5可知，无论数值模拟结果还是试验结果，该战斗部均生成5枚破片，且破片分布均呈现中心1枚周边4枚的规律，从而验证了数值计算模型与参数设置的合理性，同时也说明数值模拟方法可以用于研究破片发散角变化规律。

3.3切割网栅安装距离对发散角影响

通过数值仿真研究发现，切割网栅的安装距离及形状结构参数对战斗部破片发散角的影响较大。切割网栅的安装距离d为切割丝距药型罩罩口的距离，具体见图6。

安装距离不同导致药型罩被切割时的形状与速度大小不同，从而对生成的破片成型参数产生影响。因此，针对切割丝安装距离对发散角的影响设置了不同仿真研究方案，其中，切割丝直径为1.5mm，安装距离取0～20mm（每种情况增加5mm）。

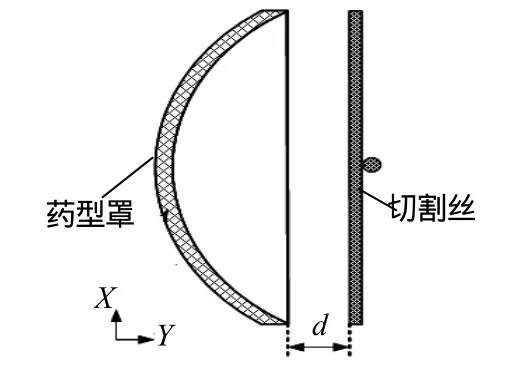
图6　切割网栅安装距离示意图Fig.6 Distance between incisive cover and liner

不同方案下破片成型具体过程如表1所示。由表1可知，随着安装距离的增加，药型罩被切割时的压垮程度随之增加，切割丝切割深度先减少后增加，在d=10mm时最小。为进一步分析破片发散角随安装距离变化规律，对其参数进行了统计，如图7所示。

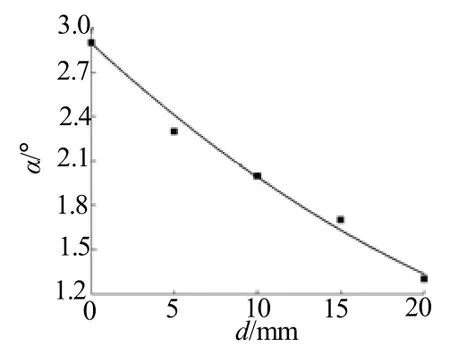
图7　破片发散角随切割丝安装距离变化曲线Fig.7 Radial dispersion angle of fragments vs the distance between incisive cover and liner

由图7可知，破片发散角随着安装距离的增加呈现出二次减小的变化规律，当安装距离由0mm增至20mm时，弹丸发散角减小了55％。

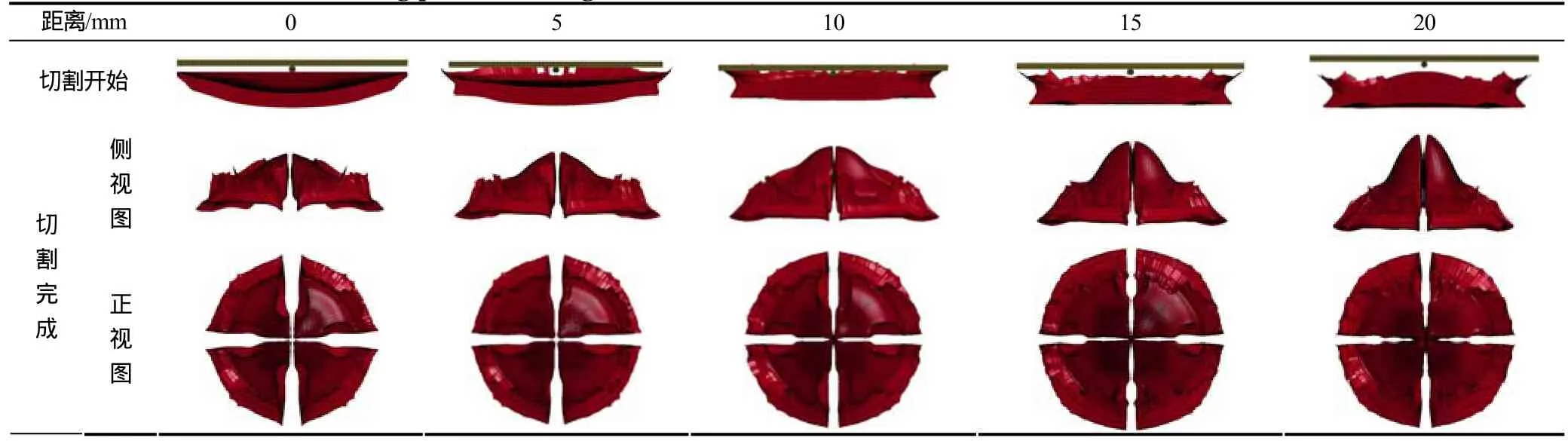
表1　不同安装距离下破片成型过程Tab.1 Forming process of fragments under different distance between incisive cover and liner

通过对图7中数据计算，得到破片发散角随安装距离的变化公式，如式（2）所示：

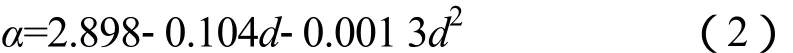
由式（2）可知，随着安装距离的增加，破片发散角逐渐减小，但当药型罩压垮形成EFP弹丸时，切割丝将无法切割药型罩形成破片；另由公式（2）可知，当安装距离为0时，破片发散角最大，因此，仅通过改变安装距离来改变发散角数值是有限的，在实际使用中必须同时改变其他参数才可以满足更大的发散角变化范围要求。

3.4切割丝形状对发散角的影响

为提高切割丝切割能力，对常用4种横截面形状的切割丝切割效果进行了数值模拟计算，4种切割丝横截面形状如图8所示。

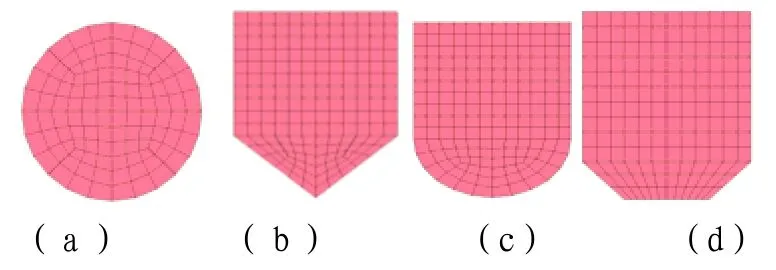
图8　4种切割杆横截面形状Fig.8 Four cross sections of incisive rod

采用切割过程中某一固定时刻药型罩被不同形状的切割丝切割的深度h来代表其切割效率。数值计算中，分取12μs和18μs 2个典型时刻的h值作为对比，结果如图9所示。

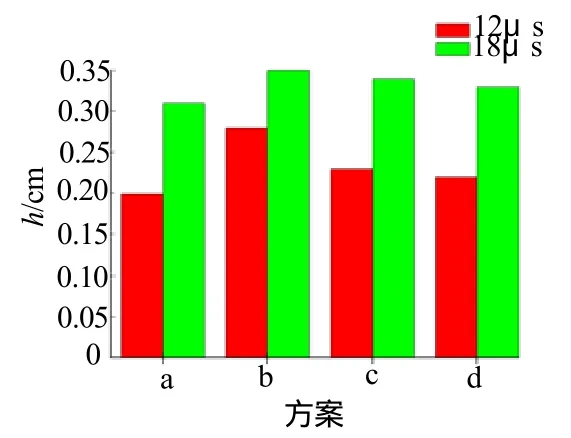
图9　4种方案的h值的对比图Fig.9 h contrast figure of four different plans

由图9可知，无论在12μs或者18μs，方案b楔形截面形状切割效率最高，且在18μs时已经将药型罩完全切割开（药型罩顶部厚度为0.35cm）。当切割丝横截面形状为圆形时，由于切割丝每个方向的长度都等于其直径，因此切割向长度l =D，但当截面形状发生变化的时候，l则为切割丝在切割方向的长度。l的变化将会影响到药型罩被切割后的运动趋势，进而影响破片的发散程度。

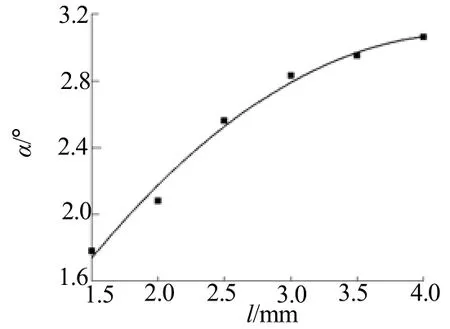
图10　破片发散角随 l变化曲线Fig.10 Radial dispersion angle of fragments vs l

为研究切割向长度对破片发散角的影响，对b方案所示的楔形截面形状切割丝进行数值计算。其中，切割丝厚度的取值范围是1.5～4.0mm。图10为发散角随切割向长度l变化曲线。由图10可以看出，破片发散角随着楔形切割丝切割向长度的增加呈现抛物线增大规律。另外通过对图10中数据拟合得到发散角随楔形切割向长度变化方程：

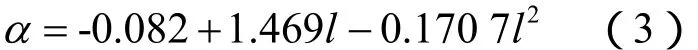
4　结论

综合以上研究结果，可得如下结论：（1）十字形切割式多破片战斗部可生成5枚、具有一定发散范围的破片，破片发散角的大小受到切割网栅的安装距离及形状的影响。（2）通过数值计算得到了十字形切割式多破片战斗部发散角随安装距离以及切割向长度的变化公式，该公式有效描述了发散角随切割网栅参数的变化规律、变化速率以及变化范围，为开展不同结构切割式多破片战斗部装药设计提供了有价值的研究参考。（3）相对于圆柱形，楔形切割丝切割效率更高，并且单位长度下发散角变化值更小，从而可以满足更加精确的发散角要求。

参考文献：

[1]Fong R,Ng W,Tang S and Thompson L．Multiple explosively formed penetrator (MEFP) warhead technology for mine and improvised explosive device (IED) neutralization[C]//.Proceedings of the 22th International Symposium on Ballistics Vancouver.BC Canada:International Ballistics Committee,2005.

[2]张洋溢,龙源,余道强,等.切割网栅作用下EFP形成多破片的数值分析[J].弹道学报,2009,21(2):90-94.

[3]李伟兵,王晓鸣,李文彬,等.隔栅对EFP破片成型及侵彻的影响[J].南京理工大学学报(自然科学版),2009,33(5):586-591.

[4]龙源,赵长啸,马海洋,等.起爆环半径对多定向破片战斗部参数的影响[J].兵工学报,2012,33(3):318-323．

[5]赵长啸,龙源,余道强,等.切割式多爆炸成形弹丸成形及对钢靶的穿甲效应[J].爆炸与冲击,2013,33(2):186-193.

Influence of Incisive Cover Factor on Radial Dispersion Angle of A Incised Multiple Fragments Warhead

ZHAO Chang-xiao1,ZHANG Yang-yi2,LU Liang3,XU Jian-guo1,ZHAO Dong-hua1,LI Hui-ming1
(1.Wuhan Ordnance NCO Academy of PLA，Wuhan，430075；2.Design & Research Institute of Guangzhou Military Area，Guangzhou，510515；3.72351 Troops,PLA ,Laiwu,271109)

Abstract：In order to improve the hit probability of incised multiple fragments warhead,based on the experimental results,the influence of incisive cover factor on radial dispersion angle was analyzed by LS-DYNA.The result shows that as the distance between incisive cover and liner increasing,the radial dispersion angle decreases.And cutting efficiency of wedge-shaped incisive cover is better than that of cylinder,as well as the change value of radial dispersion angle per unit length is smaller.

Key words：Explosive mechanicals；Multiple fragments warhead；Radial dispersion angle；Simulation

作者简介：赵长啸（1986 -），男，讲师，主要从事爆破器材应用技术研究。

收稿日期：2015-09-30

中图分类号：TJ450

文献标识码：A

文章编号：1003-1480（2016）01-0022-04