项目联合体EPC模式下基于考虑风险的Shapley值的收益分配模型

王　洁，　章恒全

(河海大学　商学院， 江苏　南京　211100)



项目联合体EPC模式下基于考虑风险的Shapley值的收益分配模型

王洁，章恒全

(河海大学商学院， 江苏南京211100)

摘要：组建项目联合体在国内EPC项目中运用广泛，而项目联合体合作成功的关键在于利润的分配。为了建立公平合理的利润分配机制，激励EPC项目联合体成员企业实现联盟，考虑成员所承担的风险，运用模糊综合评价法计算联合体成员的风险因子，并将风险因子纳入Shapley值模型，建立“基于贡献、兼顾风险”的收益分配模型，并进行数值模拟。结果表明，所建模型可以实现最大收益下的最合理的利润分配，并且考虑了风险后的分配模型不影响联合体总利润，只对优化收益根据“高风险、高回报”的原则进行合理分配，满足了公平性的要求，更体现了联合体成员的诉求。

关键词：EPC；联合体；风险因子；收益分配；Shapley值

EPC工程总承包主要是指工程总承包企业受业主委托，按照合同约定对工程建设项目的设计、采购、施工、试运行等实行全过程或若干阶段的承包[1]，该模式最早出现在20世纪60年代的美国，发展至今已逐渐成为国际承发包模式的主流趋势[2]。我国的EPC总承包模式还处于起步阶段，总承包项目规模大、过程复杂，而工程总承包企业综合实力较弱，无法满足项目的要求，因此国内在实施EPC总承包项目时，往往由设计、施工、采购等企业组成项目联合体总承包商共同实施总承包项目。在项目实施过程中，联合体成员常常无法在收益分配上达成共识，从而导致项目联合体关系破裂，耽误项目工期、质量，增加项目成本，减少利润，最终导致总承包项目的失败。因此，对于联合体实现的经济收益，要制定科学合理的分配方案，以保障项目的稳定性并且提高各参与方的积极性。

项目联合体EPC模式在国内还处于起步阶段，相关的收益分配的研究不是很多，但也有一定的研究成果。国外学者Parrod等[3]根据总承包项目的复杂、庞大等特点，指出要维持项目成员间的合作关系必须建立一个让各方满意的收益分配机制。Yuki等[4]在稳定与公平的大环境下，基于合作博弈分析联盟的利润分配，认为联盟成员成本投入越多分配的利润应该越多。国内对于收益分配主要是从博弈理论、激励理论和数学理论三个角度进行研究。从博弈角度，易欣等[5]从合作博弈角度分析了联合体收益分配问题，并运用Shapley值法建立基于成员贡献的收益分配模型。李书金等[6]针对Owen联盟结构合作博弈模型的局限性，建立了新的基于Shapley值法的收益分配方法，表明保证个人理性与集体理性是实现联盟稳定的前提。从激励角度，汪翔等[7]结合传统的Shapley值法，运用机制设计理论，建立了一个收入分配机制，实现了联盟的Pareto最优和各方的公平分配。吕萍等[8]基于总承包商与分包商的风险分担与创新性，对Shapley值法进行改进，使得利润分配更符合公平性。从数学理论的角度，刁丽琳等[9]通过对合作策略进行分解，得到对策集合后，建立多权重的Shapley值模型，并进行数值模拟。国内外学者的相关研究成果是极其宝贵的，为联合体成员收益分配模型的建立提供了借鉴。

关于联合体EPC模式下收益分配模型研究的相关文献较少，利用Shapley值法确定的模型往往是基于风险中性条件下，只考虑成员的贡献，而实际上联合体成员的风险分担能力不同，承担的风险也不同。本文运用层次分析法和熵权法确定EPC模式下，联合体成员设计企业，施工企业和采购企业的风险因子，将其纳入 Shapley值法的收益分配模型，最终建立“基于贡献、兼顾风险”的分配模型，并对其进行数值模拟。

1联合体EPC模式Shapley值法分析

1.1定义及假设

在EPC项目中，设计、施工、采购企业组成联合体对项目进行总承包，实现优化设计、管理等，获得优化收益，EPC项目的总利润π一般有以下三部分组成：

(1)

式中：Ui为参与企业的行业平均利润；B为总承包项目优化收益；G为总承包管理利润。

总承包联合体的利润分配一般包括固定和变动两部分，固定部分主要指满足个体理性的行业平均利润，变动部分主要指总承包的优化收益。联合体的收益分配主要是指对优化收益的分配，用于对成员的激励，保证项目的完成度。据此，联合体成员企业的总承包利润πi(i≠1)为：

πi=Ui+τiB-Ci

(2)

式中：τi为各成员企业分配的利润比例；Ci为各成员企业知识投入的成本

假设工程项目总承包合同造价为P，各成员均为风险中性的，成员企业参与建设的费用为合同价P的一定比例，为方便讨论，做如下定义与假设：

(1)参与企业的行业平均利润Ui

它是联合体成员企业完成正常的工作可以获得的所在行业的平均利润，一般为合同造价中设计费、施工费、采购费的一定比例，可以假设：

Ui=αiβiP

(3)

式中：αi为成员企业i参与建设的费用占合同价P的比例(∑αi=1)；βi为行业平均利润率。

(2)项目总承包优化收益B

项目总承包使得设计、施工、采购密切联系，通过优化、创新等降低项目成本，实现项目总承包的优化收益，它与成员企业的优化努力水平、优化贡献率相关，可以假设：

B=rBmax

(4)

式中：r为项目优化收益的实现程度；Bmax为项目优化后最大总承包收益，为合同总造价的一定比例，记为φP，其中0≤φ≤1，并且φ的值可以通过行业统计数据得到。

基于联合体成员优化贡献能力分配原则下，成员企业投入技术、创新等知识，获得优化收益，一般项目优化收益的实现程度r与成员企业i的优化努力程度正相关，r为努力水平的单调增函数[3]，在不失一般性的前提下，可以假设：

(5)

由此，可以得到：

(6)

式中：xi为项目优化时成员企业i的努力水平(0≤xi≤1)；ai为成员企业i的知识投入的优化贡献效率系数(0≤aI≤1，且为定值)。

(3)各成员企业知识投入的成本Ci

项目的优化收益主要是通过联合体各参与方的知识投入获得的，因此知识投入成本与项目最大总承包优化收益之间存在一定的关系。各成员企业知识投入的成本Ci与成员企业i的努力水平xi呈正相关[2]，所以Ci′>0，并且随着优化程度的不断提高，进一步实现优化收益的空间会减小，所以优化所付出的边际成本递增，即Ci″>0。由此，可以假设：

Ci=g(xi,bi)=(bixi)2φP

(7)

式中：bi为成员企业i的知识投入成本系数(0≤bi≤1，且为定值)。

1.2收益分配模型求解

1.2.1Shapley值法

Shapley值法是由Shapley于1953年提出，用来选择多人合作中分配效益最大的方案，其核心思想是按照成员对项目贡献与自身获得的收益正相关关系来分配收益[10]。EPC项目联合体可以看成是多人合作决策问题，成员的收益分配问题可以通过Shapley值法来解决，得到EPC总承包项目唯一的收益分配方案，并且在传统Shapley值法基础上，考虑风险后的分配方案与实际更贴近，因此Shapley值法有较大的优越性与合理性，适合本文研究。

(1)传统Shapley值法

当有n个人合作，形成的合作形式多种多样，产生的效益也不同，Shapley值就是得到联盟最大效益的最为合理的分配方案。

设n个参与者组成集合N，S为任意参与者组成的一个联盟，v(S)为联盟S的最大收益，ξ(S)={ξ1(v),ξ2(v)，…,ξn(v)}表示效益最大的分配方案的Shapley值，则

(8)

(2)考虑风险因子的Shapley值法

ξi′(v)=ξi(v)+ξ(v)Δθi=

(9)

当Δθi≤0，则表示成员i在联盟中承担的风险分担责任比平均值要低，分配的收益应该比风险中性时要少，减少的部分即为v(S)Δθi；反之，亦然。

1.2.2模型求解

EPC总承包项目主要是规模庞大的工业投资项目，集中在石油、化工、电站等，这类工程设计阶段就要考虑采购和施工的影响，比如许多设备和材料在设计阶段就需要提前定制，甚至需要设计生产全新的设备。因此作为联合体主办方的设计企业，总承包的主办方，一般有较强的综合实力，需要组织“方案设计—初步设计—施工图设计—施工—采购”一整套总承包任务，并且组织施工、采购企业进行优化设计，不断优化设计方案。

EPC项目联合体成员为设计、施工、采购企业，其中设计企业为联合体的主办方，其付出的优化努力水平达到最大，即x1=1。根据上述假设，可以得到：

项目总承包收益B：

(10)

联合体主办方设计企业获得的利润为：

(11)

联合体主办方对项目进行全面统筹管理，降低设计、施工、采购成本，因此总承包管理利润G通常由联合体主办方所有。

施工企业的利润：

(12)

采购企业的利润：

(13)

联合体的总利润为：

(14)

(1)求解联合体的最大总利润

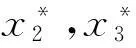
(15)

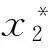
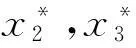
π=(α1β1+α2β2+α3β3)P+

(16)

可以看出联合体总利润最大化能够实现，当联合体获得最大利润时，施工企业和采购企业的优化努力水平与优化收益在联合体成员之间的分配比例无关；最大利润与优化收益的分配比例也无关，只与成员的优化贡献效率、知识投入成本有关。

(2)计算联合体各成员收益分配

EPC项目有3个成员企业，有7种联盟组合，各组合的联盟利润如表1所示，根据公式(8)的Shapley值法的公式可以求得在各种联盟组合下，设计、施工和采购企业各自的利益分配情况，如表2所示。

表1　联合体EPC模式各种联盟组合及其利润

表2　EPC模式下设计、施工和采购企业的收益分配计算

在项目联合体EPC模式中，联合体各方优化设计行动策略集合记为N=(1,2,3)，联合体优化设计的最终目的是实现联合体总收益最大化，Shapley值就是联合体最大总收益的最合理分配，记为π(N,v)={π1(v),π2(v),π3(v)}，πi(v)为联合体成员i分配所得的合理收益。根据表1 、表2所得数据，代入公式(8)、(9)，可以求得EPC联合体各参与方的考虑风险和未考虑风险情况下的收益。

1)未考虑风险因子时

设计企业利润：

(17)

施工企业利润：

(18)

采购企业利润：

(19)

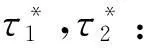
(20)

(21)

可以看出施工企业所得收益的合理分配比例与施工企业的优化贡献效率系数成正比，与知识投入成本系数成反比；与设计企业的优化贡献效率系数成反比，与知识投入成本系数不相关；与采购企业优化贡献效率系数成反比，与知识投入成本系数成正比。

2)考虑风险因子时

联合体各成员企业的利润分配如下：

πi′(v)=πi(v)+π(v)Δθi

(22)

设计企业利润：

(23)

施工企业利润：

(24)

采购企业利润：

(25)

(26)

(27)

可以看出收益的分配比例与考虑风险因子时的收益分配比例相比，多了对风险的考虑，风险承担越大，对应收益的分配也就越多。因此，在确定收益分配之前，首先要确定联合体各成员的风险分担比例。

1.2.3确定风险因子

考虑到EPC项目的特点以及所处的环境，结合前人研究结果[12～14]，确定了联合体各成员在EPC模式下承担的风险主要为以下五类，详见表3。根据风险因素可以确定各成员的风险分担比例。

表3　EPC项目风险因素

EPC联合体各成员对项目风险分担的比例主要受其风险承担能力和风险因素的影响，因此结合各参与方的风险分担能力和风险因素的组合权重确定风险分担比例。EPC项目具有较大的不确定性和模糊性，综合项目和风险的特点，选择模糊综合评价法来计算各成员的风险分担比例。风险因素的权重确定对风险分担比例的计算至关重要，在确定权重时既要反映专家学者的主观经验又要考虑客观的指标信息，因此本文采用反映主观的层次分析法和结合客观实际的熵权法来确定组合权重，使结果更加科学、合理。

(1)层次分析法

层次分析法(Analytical Hierarchy Process, AHP)是上世纪70年代的美国学者萨蒂提出的一种新的定性与定量分析结合的评价决策方法[15]。它提供了一种能够综合专家不同的主观判断并给出量化结果分析的方法，最终将问题简化为各种因素间的成对比较和简单计算，得出不同方案的权值，为决策者提供依据。AHP的基本步骤主要如下：

1)建立判断矩阵。

对指标ci(i=1,2,…,m)进行两两比较来确定矩阵要素，用cij(i,j=1,2,…,m)表示要素i对j的相对重要程度，并且根据表4的判别标度，专家打分构造判断矩阵C=(cij)m×m。

表4　判断矩阵的标度及其含义

注：若为以上两判断之间的中间状态，则对应的标度值为2,4,6,8；若j因素与i因素相比，则得到的判断值为cij=1/cji。

2)相对重要度计算

①将判断矩阵C按列规范化，得到矩阵：

(28)

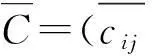
(29)

③进行归一化处理，得权重系数：

(30)

3)一致性检验

(31)

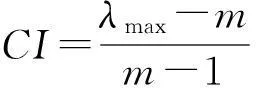
λmax=max(λi), (i=1,2,…,m)

(32)

由于两两比较法和与决策者对话得到的判断矩阵，不可能具有完全一致性，通常情况下，一致性指标不大于0.1时可认为通过一致性检验。

(2)熵权法

熵权法是一种客观赋权方法，通常来说，某个指标的熵值越小，则该指标的变异程度和提供的信息量就越多，由此权重也就越大[15]。相比于层次分析法等主观性较大的赋权方法，利用熵来计算各指标的权重，避免了主观盲目性，得到较为客观的评价结果。具体步骤如下：

1)建立风险对象集Z，Z={z1,z2,…,zm}。

2)建立风险因素评判集

根据项目各成员风险分担能力，设评判集U={较低，低，一般，较高，高}，并且对其赋值U={0.1,0.3,0.5,0.7,0.9}。

3)建立评判矩阵R

风险分担初始比例的计算根据项目各参与方对风险分担的能力以及以往的工作绩效来综合协商打分判定。评判矩阵R可以看成是风险因素集合Z到评判集U的模糊关系，矩阵R中元素rij表示第i(i=1,2,…,m)种风险由第j(j=1,2,…,n)个参与方进行分担的比例。因此，采用由项目各参与方代表组成的评估小组对项目各参与方对每个风险因素分担能力进行评价，这样就可以求出每一个风险因素有项目参与方各自分担的比例，这样m种风险计算出模糊综合评价矩阵R=(rij)m×n。

(33)

式中：δU为对应风险等级的对应值；NU为评判第j个参与方对第i种风险承担各等级风险的人数。

4)计算各指标的熵及熵权

(34)

(35)

式中：n为参与方人数；Ei为第i项指标的熵值，0≤Ei≤1；ηi为各指标的熵权。

(3)计算参与各方最终风险分担比例

1)确定层次分析法和熵权法组合权重W=(wi)m×1

(36)

2)计算风险因子

把风险分担模糊评价矩阵R与各个风险的权重集W采用加权平均算法进行模糊合成运算，最终可以得到项目各个参与方的风险分担系数σi。

σ=WR=(σ1,σ2,…,σn)

(37)

2数值模拟

设一个工程总承包项目的合同金额为P=16000万元，根据当地的市场统计资料，设计、施工、采购行业的平均利润率分别为β1=20%、β2=5%、β3=5%；设计、施工、采购企业的建设费用占合同造价的比例分别为α1=45%、α2=33%、α3=22%；设计、施工、采购企业的优化贡献效率系数分别为a1=0.55、a2=0.25、a3=0.2；设计、施工、采购企业的知识投入成本系数分别为b1=0.35、b2=0.21、b3=0.2；通过优化降低建设费用的比例为φ=100%；设计企业的管理利润为8万元。

(1)确定EPC项目参与方的风险因子

1)层次分析法确定主观权重

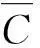
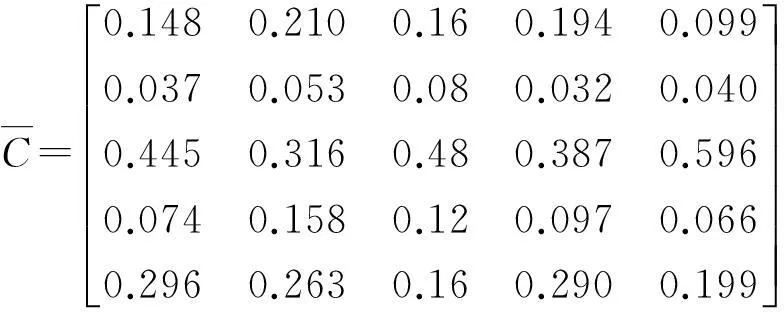
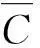
由Cφ=λφ，解得CI=0.074，λ2=5.104，λ3=5.297，λ4=5.049，λ5=5.219，所以λmax=5.297，CI=0.074。根据平均随机一致性表得当m=5时，RI=1.12[16]，所以CR=0.066<0.1，可以认为判断矩阵通过一致性检验。

2)熵权法确定客观权重

由项目3各参与方代表组成的评估小组根据风险评判集，对项目各参与方对每个风险因素的风险分担能力进行打分，并得到模糊评判矩阵R。

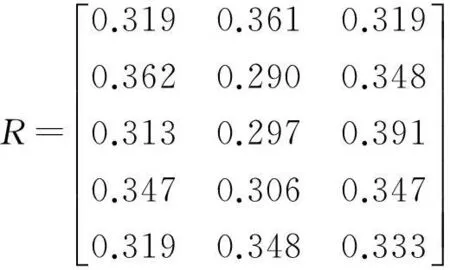
根据公式(34)、(35)，求得各指标的熵和熵权分别为：

Ei=(0.998,0.996,0.993,0.998,0.999)

ηi=(0.125,0.25,0.438,0.125,0.063)

(i=1,2,…,5)

综合(1)(2)所得结果，根据公式(36)可以求得层次分析法和熵权法组合权重W：

W=(0.079,0.047,0.764,0.05,0.06)

根据公式(37)最终得到项目各个参与方的风险因子为σj=(0.318,0.305,0.378)。

(2)计算利润分配

将所得数据代入Shapley值模型中，求得考虑风险和未考虑风险情况下的最合理的利润分配及相应的分配比例，如表5所示。

表5　考虑风险和未考虑风险时的利润分配未考虑风险

从表5可以看出，将风险因子纳入Shapley值模型中对EPC项目联合体的总利润以及施工企业和采购企业的优化努力程度没有影响。但在考虑了风险因子后，对优化收益的分配比例发生了变化，可以看到EPC项目联合体的主办方设计企业和成员企业中的施工企业都将自身的一部分利润分给了风险承担系数相对较大的采购企业，使得利润的分配更加公平。

3结语

本文从兼顾效率和公平的视角，将Shapley值法引入了以设计企业为主体的联合体EPC模式收益分配模型中，通过Shapley值法找到使得联合体总收益最大的最合理的收益分配方案。此外，本文更加综合全面地分析了联合体各成员对联盟的贡献、风险分担、努力程度、知识投入等对收益分配的影响，对Shapley值法进行修改，建立了“基于贡献，兼顾风险”的Shapley值法收益分配模型。在对考虑风险因子前后的分配模型进行比较后，发现项目风险对联合体的总收益不产生影响，但对优化收益的分配比例产生影响，风险分担较大的成员将获得更多的收益分配，符合高风险高回报的原则，极大地调动了各联盟方的优化积极性和主动性，提高项目效率。因此考虑风险因子的收益分配模型更加全面地考察了各成员企业在资金规模、风险分担方面对合作联盟的贡献度，符合联盟各方的实际利益诉求，保证收益分配的公平性，促进联合体的合作，具有参考价值和实践意义。

参考文献

[1]GB/T 5035-2005，建设项目工程总承包管理规范[S].

[2]叶堃晖，黄英，赵瑞雪. 我国EPC模式“走出去”的策略研究[J]. 科技管理研究，2015，(21)：215-218.

[3]Parrod N，Thierry C，Fargier H，et a1. Cooperative subcontracting relationship within a project supply chain：a simulation approach[J]. Simulation Modeling Practice and Theory，2007，15(2)：137-152.

[4]Kumoi Y，Matsubayashi N. Vertical integration with endogenous contract leadership: stability and fair profit allocation[J]. European Journal of Operational Research，2014，238(1)：221-232.

[5]易欣，张飞涟，邱慧. 不确定AHP和Shapley值应用于投标联合体利益分配[J]. 计算机工程与应用，2012，48(27)：194-199.

[6]李书金，张强. 一种基于Shapley值的联盟结构分配方法[J]. 北京理工大学学报，2007，27(8)：745-749.

[7]汪翔，孟卫东，吴国东. 不确定性条件下研发联盟的收入分配[J]. 系统工程，2014，32(7)：63-68.

[8]吕萍，张云，穆芬芳. 总承包商和分包商供应链利益分配研究——基于改进的Shapley值法[J]. 运筹与管理，2012，21(6)：211-216.

[9]刁丽琳，朱桂龙，许治. 基于多权重Shapley值的联盟利益分配机制[J]. 工业工程与管理，2011，16(4)：79-84.

[10]张化强，陆云鹏. 工程项目战略联盟合作及收益增值Shapley值法分配初探[J]. 建筑经济，2012，(4)：96-99.

[11]马小锋. PPP模式下交通基础设施建设项目收益分配模型研究[D]. 长春：吉林大学，2013.

[12]牛余琴. EPC总承包项目风险分担比例及收益分配研究[D]. 南京：南京航空航天大学，2014.

[13]陈志鼎，邹其伦. 基于熵权的水电EPC工程项目成本风险分析与评价[J]. 水电能源科学，2015，33(2)：168-171.

[14]杨宝臣，陈跃. EPC总承包项目综合集成风险管理[J]. 工业工程，2011，14(5)：52-57.

[15]吴凤平，陈艳萍. 现代决策方法[M]. 南京：河海大学出版社，2011.

[16]程镜霓. 基于IPD模式的工程项目风险分担研究[D]. 成都：西南石油大学，2014.

Revenue Distribution Model Based on the Shapley Value Considering the Risk Under the EPC Model

WANGJie，ZHANGHeng-quan

(School of Business, Hohai University, Nanjing 211100, China)

Abstract:The consortium is widely used in the domestic EPC projects. The key of the success of the project is the distribution of the profits. In order to establish an equitable and rational benefit allocation mechanism and motivate, to achieve the alliance of the EPC project members, the risk of members is considered, Fuzzy Comprehensive Evaluation Method is used to calculate the risk factors. Then the risk factor is put into the Shapley model, the distribution model is established which taking contribution and risk into account, then doing numerical simulation. The results show that the built model can achieve maximum benefit under the most reasonable profit distribution, and after considering the risk, allocation model does not affect the overall profit, only to optimize income according to the principle of “high risk, high return “to rational allocation, not meeting the requirements of fairness, but also reflecting the aspirations of the members of the commonwealth.

Key words：EPC; consortium; risk factor; profit distribution; shapley value

中图分类号：F224

文献标识码：A

文章编号：2095-0985(2016)02-0110-08

作者简介：王洁(1990-)，女，江苏常熟人，硕士研究生，研究方向为管理科学与工程(Email：1174764572@qq.com)

收稿日期：2015-10-29修回日期： 2015-12-05