双金属复合翅片管振动特性的研究

郭建英, 马腾飞. 刘生宝, 白艳艳(.太原理工大学 矿业工程学院；. 太原理工大学 应用力学与生物工程研究所，太原　000;.中石化宁波工程有限公司,宁波　50; .太原理工大学 机械工程学院,太原　000)



双金属复合翅片管振动特性的研究

郭建英1, 马腾飞2. 刘生宝3, 白艳艳4(1.太原理工大学 矿业工程学院；2. 太原理工大学 应用力学与生物工程研究所，太原030024;3.中石化宁波工程有限公司,宁波315103; 4.太原理工大学 机械工程学院,太原030024)

摘要：双金属复合翅片管是一种高效传热元件，容易发生流体诱导振动破坏，对其进行振动模态理论分析具有重要的工程指导意义。针对双金属复合翅片管的结构特征，将其简化为串、并联刚度系统，采用组合截面等效弯曲刚度、等效扭转刚度和等效抗拉压刚度，并结合等效质量和等效转动惯量的方法，对其弯曲、扭转和轴向振动模态进行理论解析。为了验证理论分析方法的准确性，对双金属复合翅片管的振动模态进行了实验测试和有限元分析。研究了翅片几何参数对双金属复合翅片管振动频率的影响规律。结果表明，对于矩形翅片形式的钢铝双金属翅片管，其弯曲、扭转和轴向振动频率均随翅片高度和翅片厚度的增大而减小，随翅片间距的增大而增大。

关键词：双金属翅片管；振动模态；等效截面刚度；等效质量；等效转动惯量

换热器是国民经济和工业生产领域中应用十分广泛的热量交换设备，约占设备总量的30%左右。为了提高换热器的传热效率，常用各种强化换热元件(如翅片管)代替传统光滑管[1]。翅片管有单金属翅片管和双金属复合翅片管。目前，双金属整体螺旋复合翅片换热管在国内外的应用非常广泛，已遍及能源、动力及化工加工的各种领域[2-5]。双金属复合翅片管由基管和包裹在外的整体螺旋翅片管组成，基管的材质可根据热流体腐蚀情况和工作压力选定，通常为碳钢、不锈钢或铜；外管可选用延展性好，抗大气腐蚀能力强，传热性能优良的金属，如铝或铜；将铝管或铜管套在基管外面，然后用专用轧机将铝或铜管挤压成翅片，同时在基管外形成一层薄的底层将基管紧紧裹住。

换热器在使用过程中，极容易产生流体诱导振动[6-7]，它会导致剧烈的噪声及换热管的断裂损坏。有效预防和控制换热器流体诱导振动破坏的首要措施是，将换热管的固有振动频率和流体干扰力频率分隔开。因此，换热器的设计必须进行振动计算，即准确计算换热管的固有振动频率[8]。双金属整体螺旋翅片管在结构上属于不同材料的双层壳体复合结构，且外管由翅片组成，其截面刚度与质量沿轴向分布不均匀。目前，虽然采用有限元法可以获得双金属复合翅片管较精确的动力学特性，但不便于工程设计采用。建立准确的双金属复合翅片管振动频率计算模型，对双金属翅片管换热器的设计具有重要的理论指导和工程应用价值。

对于双层壳体复合结构，谢志勇等[9-11]的研究发现，内外壳的耦合作用会影响其动态特性。而对于翅片管，工程上常采用经验公式将其简化为有效直径的光滑管，但计算结果误差较大。

本文拟将双金属翅片管看作串、并联刚度组合系统，采用组合截面等效刚度法并结合等效质量和等效转动惯量，推导双金属复合翅片管弯曲、扭转及轴向振动模态特性的理论解析模型；并采用实验测试和有限元模拟的方法对理论结果进行验证；同时分析不同翅片几何尺寸时双金属复合翅片管振动频率的变化规律。

1双金属复合翅片管几何结构

双金属复合翅片管为两种不同材料的组合管，内外管之间牢固连接而无相对错动；外管翅片形状为矩形，且翅片高而薄，其结构如图1所示。图1中，管子总长为L，内管内径为D1，外径为D2，内管材料的杨氏弹性模量为E1，剪切弹性模量为G1，密度为ρ1。外翅片管内径为D2，翅根直径为D3，翅顶直径为D4，翅片高度为h，翅片厚度为a，翅片间距为b，外翅管材料的杨氏弹性模量为E2，剪切弹性模量为G2，密度为ρ2。

图1　双金属复合翅片管几何结构与参数Fig.1 The geometry and parameters of bimetallic finned tube

2双金属复合翅片管弯曲振动模态

2.1理论解析

在横向载荷激励下，双金属复合翅片管的振动模态为弯曲振动。假设双金属翅片管为线弹性体，材料均匀连续，各向同性，且振动过程中各截面仍保持为平面。由于双金属翅片管的长度远大于其直径，为细长结构，因此采用Bernoulli-Euler梁理论建立其横向弯曲自由振动动力学方程：

(1)

式中，y(x,t)为距原点x处管子截面在t时刻的横向位移。

由图1可知，双金属翅片管的刚度和质量沿轴向(x方向)分布不均匀。为了便于解析，本文将双金属翅片管等效为等截面管，并将EeIe定义为双金属翅片管的等效截面弯曲刚度，me定义为单位长度的等效质量。求解该微分方程，得双金属翅片管弯曲振动的各阶固有频率为：

(2)

式中，λwi(i=1, 2, 3,…)为各阶弯曲振动频率常数，取决于边界支撑条件。

由式(2)可知，准确获得双金属复合翅片管的等效截面弯曲刚度EeIe及其等效质量me是精确解析其弯曲振动频率的关键。为此，基于质量等效原则，本文将图1所示的双金属复合翅片管的螺旋结构简化为槽状结构，再根据其翅片周期性分布的结构特征，选取其中一个翅片单元，并利用组合截面法来推导其等效截面弯曲刚度和等效质量。图2(a)为简化后的双金属复合翅片管槽状结构，图2(b) 为一个翅片单元的几何参数示意图。

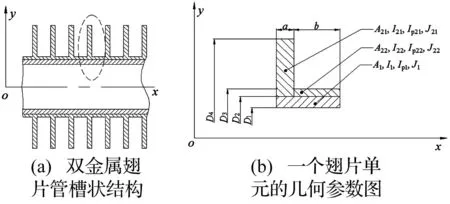
图2　双金属翅片管槽状结构和一个翅片单元的几何参数图Fig.2 Simplified trough-like geometry of bimetallic finned tube and the geometry diagram of a fin unit

从图2(a)可以看出，双金属复合翅片管相当于内管与外翅管的并联刚度系统，而外翅管可看做不同截面管段的串联刚度系统。对图2(b)所示的一个翅片单元管段(长度为a+b)而言：内管(内径D1，外径D2)的截面刚度沿轴向(x方向)均匀分布，定义其横截面积为A1，其截面对中性轴的惯性矩为I1，其截面的极惯性矩为Ip1，该部分管段的转动惯量为J1。相应长度的外翅管相当于两段阶梯截面的串联刚度系统，其中含翅片部分(内径D2，外径D4)，定义其横截面积为A21，该截面对中性轴的惯性矩为I21，截面的极惯性矩为Ip21，该部分转动惯量为J21；不含翅片部分(内径D2，外径D3)，定义其横截面积为A22，该截面对中性轴的惯性矩为I22，截面的极惯性矩为Ip22，该部分转动惯量为J22。这些参数的值分别为：

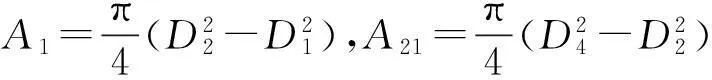
(3)

(4)

(5)

J1=(a+b)ρ1Ip1，J21=aρ2Ip21，J22=bρ2Ip22

(6)

对于这样的串、并联刚度系统的组合截面，可以推导出其等效截面弯曲刚度为：

(7)

另外，可以推导出双金属复合翅片管单位长度的等效质量为：

(8)

这样，将式(7)、(8)代入式(2)，可以解出双金属复合翅片管的各阶弯曲振动固有频率。

2.2实验测试

为了验证等效刚度法解析双金属复合翅片管弯曲振动模态方法的精确性，本文采用北京东方振动和噪声技术研究所的INV3018A智能信号采集系统和DASP-V10振动信号分析系统，并用捶击法对钢铝双金属复合翅片管在两端自由状态下的横向弯曲振动固有频率进行了实验测试。两端自由支撑条件是通过采用两条高弹性皮筋悬挂翅片管的方法实现的。实验测试所用的双金属复合翅片管的内基管为碳钢管，外管为铝翅片管，结构几何参数见表1。实验测试获得了两端自由状态下，钢铝双金属复合翅片管振动模态的自谱-FFT分析的幅值谱(PEAK)图，如图3所示。

表1　钢铝双金属复合翅片管结构

图3　实测幅频特性曲线Fig.3 Measured amplitude-frequency characteristic curve

2.2有限元分析

本文采用有限元软件ANSYS对钢铝双金属复合翅片管进行了模态分析。实验测试用的翅片管为整体螺旋结构，在进行理论解析时将其简化为槽状翅片管结构。在进行有限元分析时，分别建立了两种模型，一种为槽状翅片管模型，见图4(a)；另一种为螺旋翅片管模型，见图4(b)。有限元模型的几何尺寸与实验用管完全相同，单元类型采用四面体10节点三维实体单元，内外管之间无相对错动的牢固连接通过GLUE操作来实现。

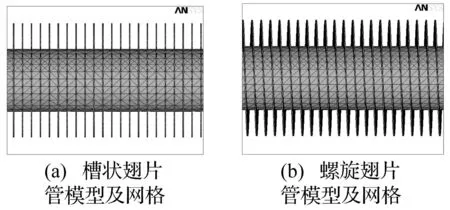
图4　槽状翅片管模型及网格和螺旋翅片管模型及网格 Fig.4 Trough-like and Helix model and mesh of bimetallic finned tube

2.3弯曲振动频率结果分析

表2显示了两端自由条件下，钢铝双金属复合翅片管前四阶弯曲振动固有频率的实测值、有限元模拟值及理论解析值的比较。在表2中，误差1指的是理论解析值与螺旋状模型有限元分析值之间的差别，误差2指的是理论解析值与实测值之间的差别。表2数据表明，① 对双金属复合翅片管振动模态进行有限元分析时，槽状模型和螺旋状模型的分析结果非常接近，说明将双金属整体螺旋翅片管简化为槽状模型是可行的。② 采用等效截面弯曲刚度EeIe并结合等效质量me，计算得到的双金属复合翅片管的前四阶弯曲振动固有频率，与实测值相比，一阶频率误差为5.00%；四阶频率误差为6.96%。通过分析发现该误差产生的主要原因是，实测用的双金属翅片管的几何尺寸加工不均匀。如实测的双金属翅片管的单位长度质量me为1.386 kg/m，而按照实测的管子几何参数计算得到的单位长度质量me为1.302 kg/m，二者误差达到6.06%。这种加工不均匀同样会影响管子的弯曲刚度，最终使振动频率的解析值与实测值之间产生大的误差。③双金属翅片管前四阶弯曲振动固有频率的解析值与有限元模拟值相比，一阶频率误差最小，仅为1.39%；四阶频率误差最大，为3.63%；这表明采用等效刚度法并结合等效质量解析双金属复合翅片管的弯曲振动模态是精确的。

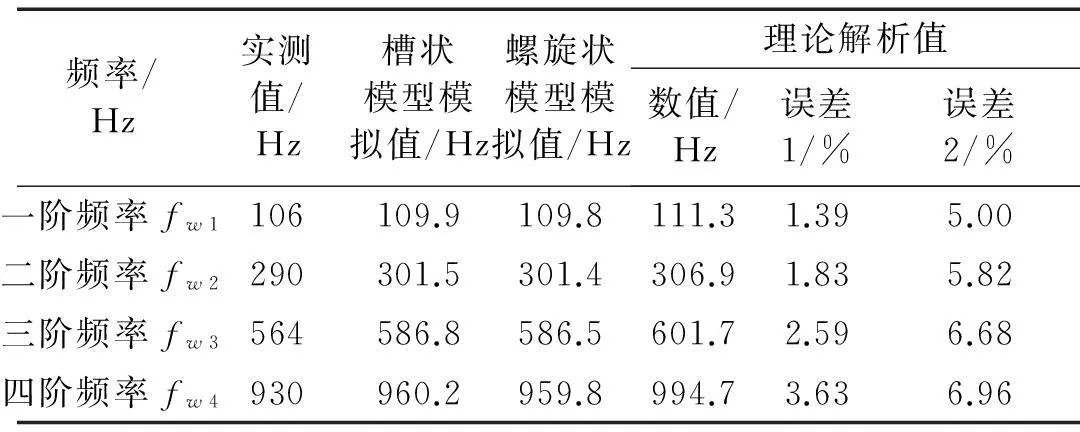
表2　双金属复合翅片管弯曲振动固有频率

3双金属复合翅片管扭转与轴向振动模态

3.1扭转振动模态解析

在扭矩激励下，双金属复合翅片管表现为扭转振动模态。扭转振动为高阶模态，必须考虑转动惯量的影响，因此其扭转自由振动的动力学方程为：

(9)

式中，θ(x,t)为在距原点x处截面在t时刻的角位移。与弯曲振动解析方法相同，这里将GeIpe定义为双金属翅片管的等效截面扭转刚度，Je定义为其单位长度的等效转动惯量。求解得双金属翅片管扭转振动的各阶固有频率为：

(10)

式中，λni(i=1, 2, 3…)为各阶扭转振动频率常数，取决于边界支撑条件。同样，对于双金属翅片管这样的串、并联刚度系统的组合截面，可以推导出其等效截面扭转刚度为：

(11)

而其单位长度的等效转动惯量为：

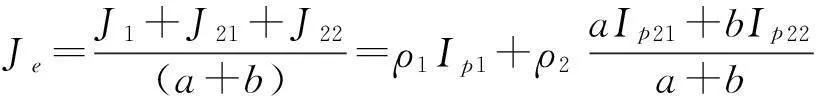
(12)

这样，将式(11)、(12)代入式(10)，可以解出双金属复合翅片管的各阶扭转振动固有频率。

3.2轴向振动模态解析

在轴向载荷激励下，双金属复合翅片管的轴向自由振动的动力学方程为：

(13)

式中，u(x,t)为距原点x处截面在t时刻的轴向位移。同样，将EeAe定义为双金属复合翅片管的等效截面抗拉压刚度，me为其单位长度等效质量。求解可得双金属翅片管的各阶轴向振动固有频率为：

(14)

式中，λli(i=1, 2, 3,…)为各阶轴向振动频率常数，取决于边界支撑条件。

同样采用串、并联刚度法，可以推导出双金属翅片管的等效截面抗拉压刚度为:

(15)

将式(15)、(8)代入式(14) 可以获得其各阶轴向振动固有频率。

3.3扭转和轴向振动频率结果分析

表3显示了两端自由条件下，钢铝双金属复合翅片管扭转与轴向振动固有频率的有限元模拟值及理论解析值的比较，其中管子几何参数同表1。在表3中，误差指的是理论解析值与螺旋状模型有限元分析值之间的差别。从表3可以看出，① 槽状模型与螺旋状模型对于扭转振动和轴向振动固有频率的分析结果也非常接近，进一步表明对双金属螺旋翅片管振动模态进行分析时，将其简化为槽状模型是可行的。② 采用等效截面扭转刚度GeIpe并结合等效转动惯量Je，计算得到的双金属复合翅片管的前两阶扭转振动固有频率，与有限元值相比，一阶频率误差为1.41%，二阶频率误差为1.25%。这说明该解析方法具有较高精度。③ 采用等效截面抗拉压刚度EeAe并结合等效质量me，计算得到的双金属复合翅片管的轴向振动固有频率，与有限元值相比，一阶频率误差为3.87%，二阶频率误差为31.4%。本文经分析发现，这个误差产生的主要原因是，在管子轴向振动时，翅片会同时沿轴向产生弯曲振动(相当于环形薄板的弯曲振动)，二者耦合作用会对管子的轴向振动频率，尤其是高阶频率产生较大影响。这种影响可以从管子的轴向振动模态振型图中得到进一步验证，如图5(h)和图5(j)所示。

图5为双金属复合翅片管各阶模态振型。从图中可以看出，双金属翅片管的弯曲和扭转模态振型与光滑管完全相同，但其轴向振动的模态振型却有不同。由图5 (h)，(j)可以看出，在管子轴向振动时，翅片沿轴向发生倒伏现象，即翅片沿管子轴向发生弯曲振动，二者耦合作用会对翅片管的轴向振动频率产生重要影响。因此，式(14)由于没有考虑翅片沿轴向的弯曲振动而产生较大误差。另外需要注意的是，管子轴向振动时，翅片会沿轴向出现双向反复倒伏现象，这时翅片由于受到交变载荷作用容易产生疲劳破坏，即翅片会在根部断裂而丧失传热作用。

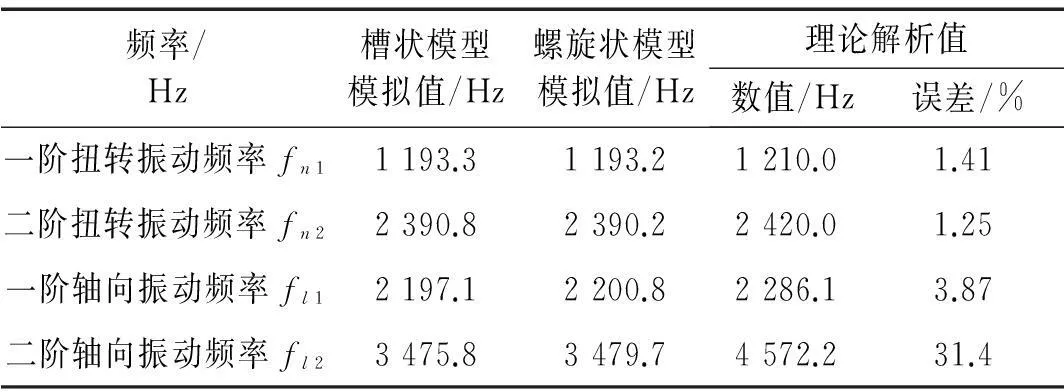
表3　双金属复合翅片管扭转和轴向振动固有频率

图5　双金属复合翅片管各阶模态振型Fig.5 Modal shapes of bimetallic finned tube

4不同翅片几何参数时双金属复合翅片管的振动频率

换热管设置翅片是为了增加传热面积。翅片几何参数，如翅片高度h、翅片厚度a和翅片间距b是影响传热面积的重要因素。为满足不同的传热要求，工程中需设计不同的翅片几何参数， 而翅片几何参数的变化会直接影响翅片管的刚度和质量，从而改变整个管子的振动频率。 表4～表6显示了翅片几何参数对钢

铝双金属复合翅片管振动频率的影响规律和影响程度，其中管子的基本几何参数D1，D2，D3和D4见表1。

由表4可知，① 对于钢铝双金属复合翅片管，当其翅片高度h由0 mm增大到12 mm时，在两端自由边界条件下，其一阶弯曲固有频率(以下均指螺旋状模型的有限元分析值)由122.7 Hz降低到104.9 Hz，降低幅度为14.5%；其一阶扭转固有频率由1 571.4 Hz降低到1 026.0 Hz，降低幅度为34.6%；其一阶轴向固有频率由2 545.1 Hz降低到1 794.2 Hz，降低幅度为29.5%。②对不同的翅片高度，一阶弯曲和扭转振动频率的解析值与有限元值均非常吻合，最大误差仅为1.57%。③ 一阶轴向振动频率的解析值与有限元值相比，其误差随翅片高度的增加而增大。当翅片高度h小于或等于9.0 mm时，误差最大值为3.87%；当翅片高度h为12 mm时，误差达到21.71%。这进一步表明翅片沿轴向的弯曲振动会对管子的轴向振动频率产生大的影响，且翅片越高，影响越大。但在工程实际中，翅片太高容易在翅片间隙积尘，不利于传热，因此实际翅片高度会有所限制。

由表5可知，① 当翅片厚度a由0.35 mm增大到0.80 mm时，其一阶弯曲频率的降低幅度为8.6%，一阶扭转频率的降低幅度为15.9%，一阶轴向频率的降低幅度为6.4%。② 对于不同的翅片厚度，管子的一阶弯曲、扭转和轴向振动频率的解析值均与有限元值较为吻合，一阶轴向频率的误差最大，为3.87%。

由表6可知，① 当翅片间距b由2.8 mm增大到4.75 mm时，其一阶弯曲频率增大4.2%，一阶扭转频率增大9.9%，一阶轴向频率增大7.0%。② 对不同的翅片间距，管子的一阶弯曲、扭转和轴向振动频率的解析值也与有限元值非常吻合，最大误差仍为轴向频率的误差，为3.87%。

另外，由式(2)、(10)和(14)可知，翅片几何参数对双金属翅片管振动频率的影响规律在不同边界支撑条件下是相同的，在高阶频率下也是相同的。因此可以说，对于矩形翅片的钢铝双金属翅片管，在任意边界条件下，管子的各阶弯曲、扭转和轴向振动频率均随翅片高度h和翅片厚度a的增大而减小，随翅片间距b的增大而增大。

表4　不同翅片高度时双金属翅片管的固有频率 (a=0.35 mm，b=2.80 mm)

表5　不同翅片厚度时双金属翅片管的固有频率(h=9.0 mm，b=2.8 mm)

表6　不同翅片间距时双金属翅片管的固有频率(h=9.0 mm，a=0.35 mm)

5结论

(1) 将双金属复合翅片管结构简化为串、并联刚度系统，采用组合截面等效弯曲刚度、等效扭转刚度和等效抗拉压刚度，并结合等效质量和等效转动惯量的方法，对其弯曲、扭转和轴向振动模态进行理论解析。其中，弯曲和扭转振动频率的理论解析值与有限元分析值相比，误差较小；而轴向振动频率的误差相对较大，主要原因是没有考虑翅片沿管子轴向的弯曲振动对管子轴向振动的耦合作用。

(2) 翅片几何参数对双金属复合翅片管的振动频率有重要影响。对于矩形翅片的钢铝双金属翅片管，管子的各阶弯曲、扭转和轴向振动频率均随翅片高度h和翅片厚度a的增大而减小，随翅片间距b的增大而增大。

(3) 对双金属螺旋翅片管振动模态进行有限元模拟时，将其简化为槽状结构产生的误差很小。

参 考 文 献

[ 1 ] Goldstein R J, Ibele W E, Patankar S V. Heat transfer—A review of 2004 literature [J]. International Journal of Heat and Mass Transfer, 2010, 53:4343-4396.

[ 2 ] Kuntysh V B, Sankovich E S, Mulin V P. An energy-saving nondestructive tester for the thermal performance of bimetallic finned tubes [J]. Chemical and Petroleum Engineering, 2007, 43(3/4):227-233.

[ 4 ] 杨小琼, 王启杰, 王晓军.翅片管接触热阻的理论预测和试验研究[J]. 化工学报, 1996, 47(4): 427-432.

YANG Xiao-qiong, WANG Qi-jie, WANG Xiao-jun. heoretical prediction and experimental investigation of finned tubes thermal contact resistance [J]. Journal of Chemical Industry and Engineering, 1996, 47(4): 427-432.

[ 5 ] 刘伟军, 付国民, 张书华. Al—Cu翅片管的单管换热及阻力特性[J]. 哈尔滨理工大学学报, 1996, 1(1): 17-20.

LIU Wei-jun, FU Guo-ming, ZHANG Shu-hua. Convective transfer and resistance characteristics of single aluminum-copper fin-tube [J]. Journal of Harbin University of Science and Technology, 1996, 1(1): 17-20.

[ 6 ] Longatte E, Baj F, Hoarau Y, et al. Advanced numerical methods for uncertainty reduction when predicting heat exchanger dynamic stability limits: Review and perspectives [J]. Nuclear Engineering and Design, 2013, 258:164-175.

[ 7 ] Goyder H G D. Flow induced vibration in heat exchangers [J]. Institution of Chemical Engineers, 2001, 80, Part A: 226-232.

[ 8 ] GB151-1999. 管壳式换热器[S]. 北京: 中国标准出版社, 1999.

[ 9 ] 谢志勇, 周其斗, 纪刚. 双层柱壳的流固耦合模态计算与试验研究[J]. 海军工程大学学报, 2009, 21(2): 97-101.

XIE Zhi-yong, ZHOU Qi-dou, JI Gang.Computation and measurement of double shell vibration mode with f luid load [J]. Journal of Naval University of Engineering, 2009, 21(2): 97-101.

[10] 金广文, 何琳, 姜荣俊. 流固耦合对双层圆柱壳体振动特性的影响[J]. 武汉理工大学学报:交通科学与工程版, 2007, 31(5): 882-885.

JIN Guang-wen，HE Lin，JIANG Rong-jun. Influence of fluid-structure coupling for vibration transmissibility of ribbed cylindrical double-shell [J]. Journal of Wuhan University of Technology:Transportation Science & Engineering, 2007, 31(5): 882-885.

[11] 魏建辉, 陈美霞, 乔志李，等. 湍流激励下单双层圆柱壳振动特性对比[J]. 华中科技大学学报:自然科学版, 2012, 40(8): 44-48.

WEI Jian-hui, CHEN Mei-xia, QIAO Zhi-li, et al. Comparing the vibration characteristics of single cylindrical shells and double ones excited by turbulent boundary layers [J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2012, 40(8): 44-48.

Vibration characteristics of bimetallic finned tubes

GUOJian-ying1,MATeng-fei2,LIUSheng-bao3,BAIYan-yan4(1. College of Mining Engineering, Taiyuan University of Technology, Taiyuan 030024, China; 2. Institute of Applied Mechanics and Biomedical Engineering, Taiyuan University of Technology, Taiyuan 030024, China; 3. Sinopec Ningbo Engineering Co., Ltd., Ningbo 315103, China; 4. College of Mechanical Engineering, Taiyuan University of Technology, Taiyuan 030024, China)

Abstract:Bimetallic finned tubes are highly efficient heat transfer components, and they are easy to have flow-induced vibration damages. Their modal analysis has an important engineering significance. A bimetallic finned tube was simplified as a system with series and parallel stiffnesses according to its structural characteristics. The bending, torsion and axial vibration modes of the bimetallic finned tube were analyzed theoretically by using the methods of equivalent cross-sectional bending stiffness, equivalent torsion stiffness and equivalent tension-compression stiffness combined with the equivalent mass and equivalent moment of inertia. The tests and finite element analysis for vibration modes of bimetallic finned tubes were conducted in order to verify the correctness of the theoretical methods. The effects of fin geometry on the natural frequencies of a steel-aluminum bimetal finned tube with rectangular fins were investigated. The results showed that its bending, torsional and axial vibration natural frequencies decrease with increase in fin height and fin thickness, and increase with increase in fin pitch.

Key words:bimetallic finned tubes; vibration modes; equivalent cross-sectional stiffness; equivalent mass; equivalent moment of inertia

中图分类号:TB123

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.05.033

收稿日期：2015-02-02修改稿收到日期：2015-03-15

基金项目：山西省自然科学基金(2013011025-2)

第一作者 郭建英 女，博士，副教授，1972年11月生