人-桥竖向耦合振动计算方法

谢　旭， 钟婧如， 张　鹤， 张治成(浙江大学 土木工程系，杭州　310058)



人-桥竖向耦合振动计算方法

谢旭， 钟婧如， 张鹤， 张治成(浙江大学 土木工程系，杭州310058)

摘要：为了分析轻质人行桥的人-桥竖向耦合振动，建立了基于双脚支撑人体计算模型的人-桥耦合振动方程。根据行人在刚性地面行走时的步伐荷载计算结果与文献给出的步伐荷载时程曲线对比，验证了双脚支撑人体计算模型能较好地模拟行人的脚步力特性并讨论了合理的人体参数取值范围。以一座跨度22.8 m、第一阶竖弯自振频率7.23 Hz的铝合金人行桥为例，运用Monte Carlo法模拟人群的步行参数，形成不同密度人群过桥的随机工况，并用直接积分法计算了考虑人群-桥竖向耦合振动的铝合金人行桥动力响应。计算结果表明，当人群密度较大时，考虑人桥耦合的人致振动卓越频率趋于分散，其振动响应明显小于不考虑耦合影响的计算结果。

关键词：人行桥;耦合振动;舒适性;步伐荷载;随机人群

随着轻质高强材料在人行桥建设中的推广应用，改进人行桥振动舒适性验算方法是完善桥梁结构设计的重要工作[1]。目前，国内外对人行桥的振动舒适性验算主要有两种方法：一是采用结构的自振频率，如我国《城市人行天桥与人行地道技术规范》(CJJ69-95)[2]规定结构的竖向自振频率不小于3.0 Hz；另一种是采用结构的振动响应，如德国EN03等标准[3-5]根据步伐荷载作用下的振动响应验算桥梁的舒适性。与前者相比，后者考虑了步行荷载和结构的动力特性，通用性强，已经成为研究人行桥舒适性问题的主要方法[6]。

自20世纪70年代以来，用于人行桥动力计算的步伐荷载模型以及基于结构动力响应的舒适性验算方法得到了很大改进[7-14]。但是，既有的算法一般不考虑人-桥相互作用，而是将行人激励以外荷载的形式施加于桥面[15]。2000年伦敦千禧桥发生严重的侧向振动问题，促使许多学者对人行桥侧向耦合振动进行大量研究，如Dallard[16]提出了侧向振动线性自激励模型，Ingolfsson[17]运用振动装置研究了桥面振动对行人侧向步行力的影响，袁旭斌[18]根据振动台试验结果研究结构振动对步伐力的影响，宋志刚等[19]提出了基于动力放大系数的结构动力响应简化计算方法。

相对于侧向振动而言，目前关于人-桥竖向耦合振动的研究较为欠缺。轻质人行桥由于自重轻、刚度小，在步伐激励下竖向动力特性变化大，耦合作用对桥梁的竖向振动响应会产生不可忽视的影响[20-21]。为了分析这类影响，李红利等[22]基于双脚支撑的人体动力学模型建立了考虑人-桥耦合振动的运动方程，并试验研究了人-桥动力相互作用的整体效应，给出以单人形式描述的人桥动力相互作用理论表达式；Qin等[23]用双脚支撑人体模型建立了简支梁在单人过桥时的人-桥耦合振动计算方法，但采用的计算方法不便于考虑任意的随机人群脚步荷载作用。本文在文献[23]的基础上用直接积分法建立基于双脚支撑人体模型的人-桥耦合振动计算方程，并讨论行走模型的参数取值范围。以一座跨度为22.8 m的铝合金人行天桥为例，运用Monte Carlo法随机模拟步行参数，计算不同密度人群作用下的人-桥耦合振动响应，分析人-桥耦合振动对轻质人行桥结构振动响应的影响。

1人-桥竖向耦合振动计算方法

1.1步伐荷载模型

图1为双脚支撑的人体行走模型。人体由集中质量(COM)和刚体-弹簧-阻尼系统模拟。图中，下标l和t分别表示前后脚，k和c表示腿部的刚度和阻尼，θ为腿与桥面的夹角，xc和yc为重心位置纵向和竖向位移。前脚落地瞬间假定腿与桥面的攻角为θ0，这时前腿为自然长度，支点反力为零，人体的竖向平衡依靠后腿支撑。当人体处于单脚支撑状态时，可作为双脚支撑的一个特例来考虑。

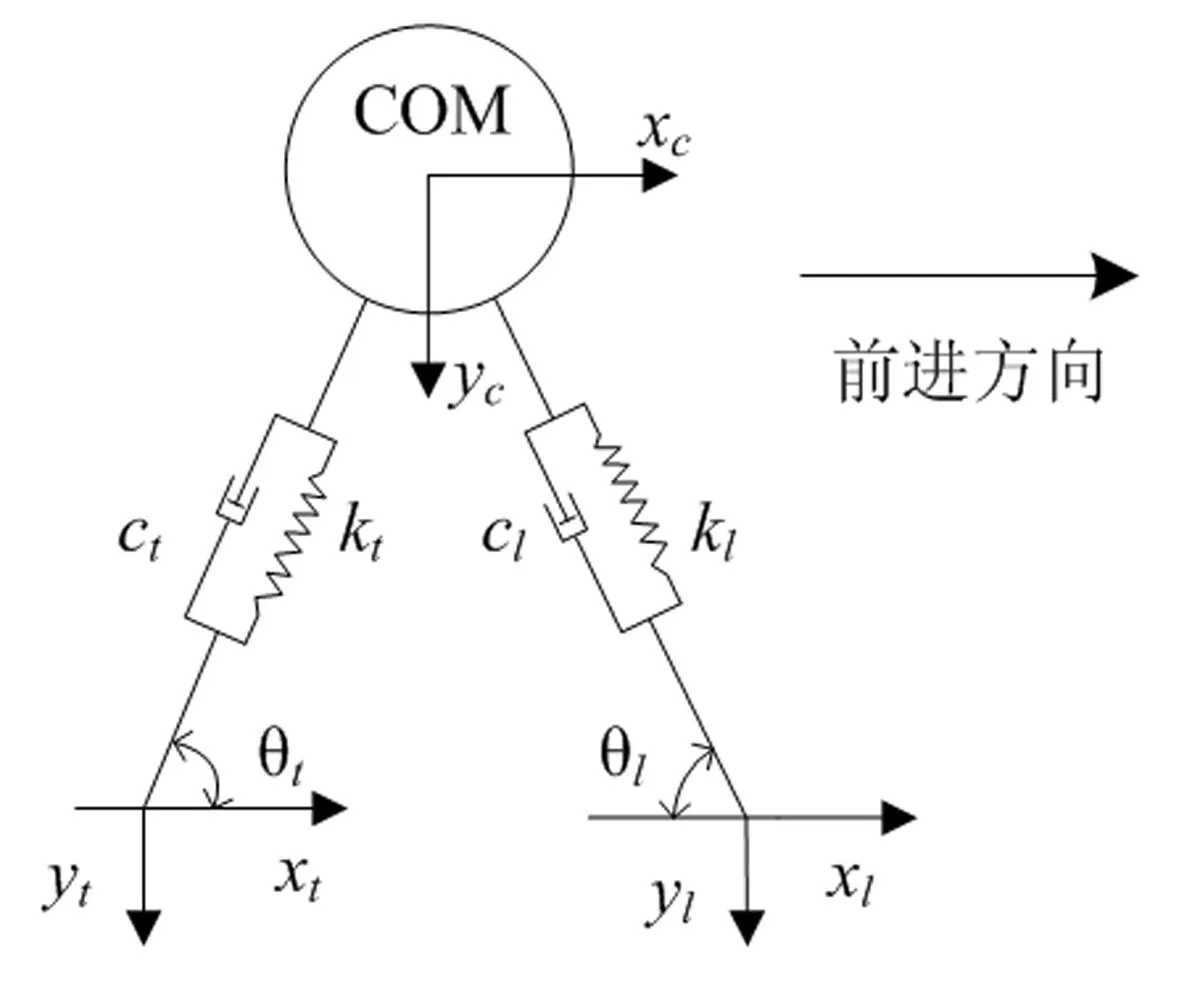
图1　双脚支撑模型Fig.1 Bipedal walking model

人体集中质量(COM)的受力分析如图2所示。图中S表示腿的恢复力，D为腿的阻尼力。假定人体沿桥梁纵向匀速前进，则可根据腿与桥面的夹角，建立如下的单自由度动平衡方程：

(1)

式中，m为人体质量，g为重力加速度。

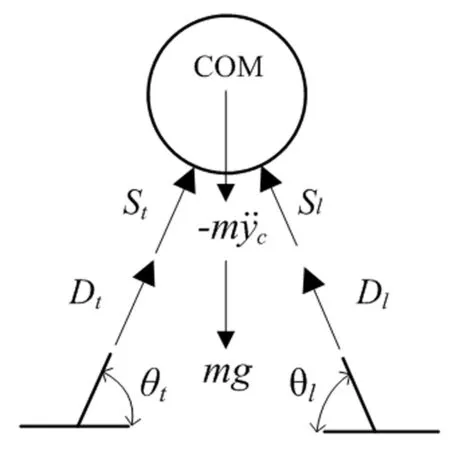
图2　集中质量(COM)受力状态Fig.2 Forces exerted on the center of body(COM)

腿的恢复力S和阻尼力D分别由腿部的刚度k和阻尼系数c计算得到，即：

(2)

式中，Δl和Δv为腿长的改变量和腿上下端的相对速度，下标l、t的含义同前。恢复力和阻尼力均设定为不小于零的值。考虑桥面竖向与纵向振动影响的腿长变化以及相对速度分别按式(3)、式(4)计算：

(3)

(4)

式(3)中，Lleg为腿的自然长度，由图3所示的前脚落地瞬间人体计算模型得到。图3中L0为步长；重心和前脚落地点的距离与步长的比值用λCOM表示；上标“·”表示变形对时间的一阶导数，即速度。为了尽量消除初始条件对计算的影响，以进桥前的直立、且单点支撑姿势作为初始状态(如图4)，这时可假定人体竖向的初加速度、初速度为零。其中，H0为初始状态人体重心的高度，根据人体重量以及腿的轴向刚度确定，即：

H0=Lleg-mg/kl

(5)

图3　前脚落地瞬间人体计算模型Fig.3 Bipedal walking model when the leading limb contacts the ground

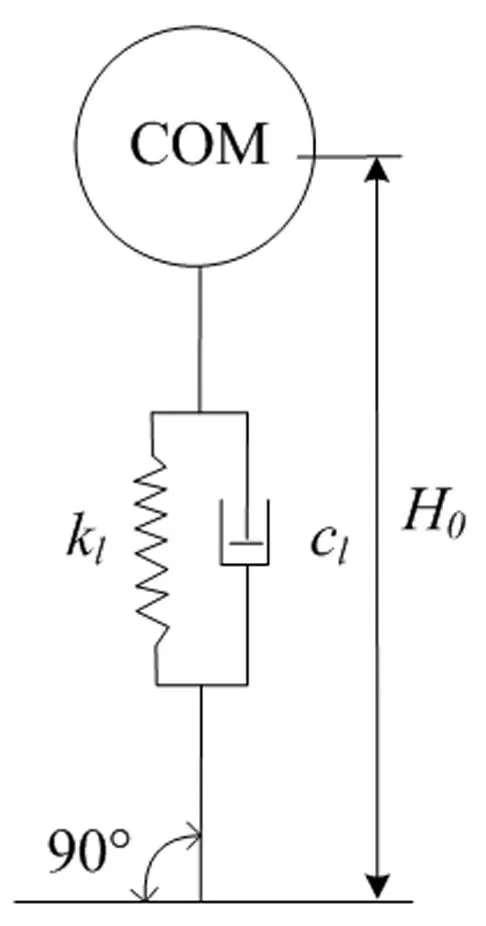
图4　行走初始状态Fig.4 Initial state in walking

桥面在脚步落地点受到的步伐荷载根据图5的关系可以表示成为：

(6)

式中，Fy、Fx分别为脚步的竖向和纵向反力，下标l,t的含义同前。

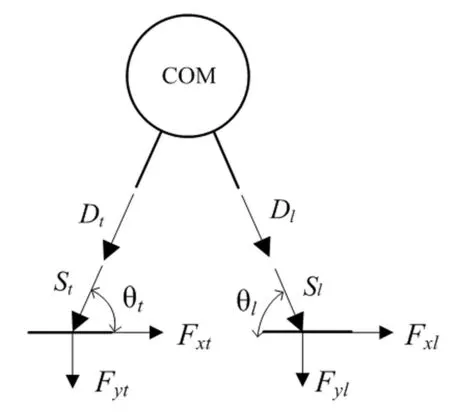
图5　桥面受力状态Fig.5 Forces exerted on the deck

1.2计算模型验证以及人体参数影响分析

为了检验上述算法并讨论合理的人体参数取值范围，图6给出了人体行走模型以1.5 Hz步频在刚性地面行走时的竖向动荷载系数αy(t)与文献[24]的结果对比，这里αy(t)为竖向步伐荷载与人体自重的比值，定义详见式(8)。因两者的脚步力接触时间略有差异(按本文模型计算得到的脚步力接触时间约为文献[24]的90%)，这里将接触时间按等比例调整到一致。计算时假定行人体重为0.7 kN；腿部刚度k与脚步的初始攻角θ0参考相关文献分别取16 kN/m及69°[23,25-26]；阻尼系数c及行人重心位置λCOM分别近似地取为0.14 kN·s/m和0.53；根据文献[27]给出的数据,可拟合得到步长与频率f关系为：

L0=0.45+0.007 41ef/0.54

(7)

图6表明，由本文方法得到的脚步力时程与文献结果基本一致，说明本文方法能较好地模拟竖向走行步伐荷载的基本特性。

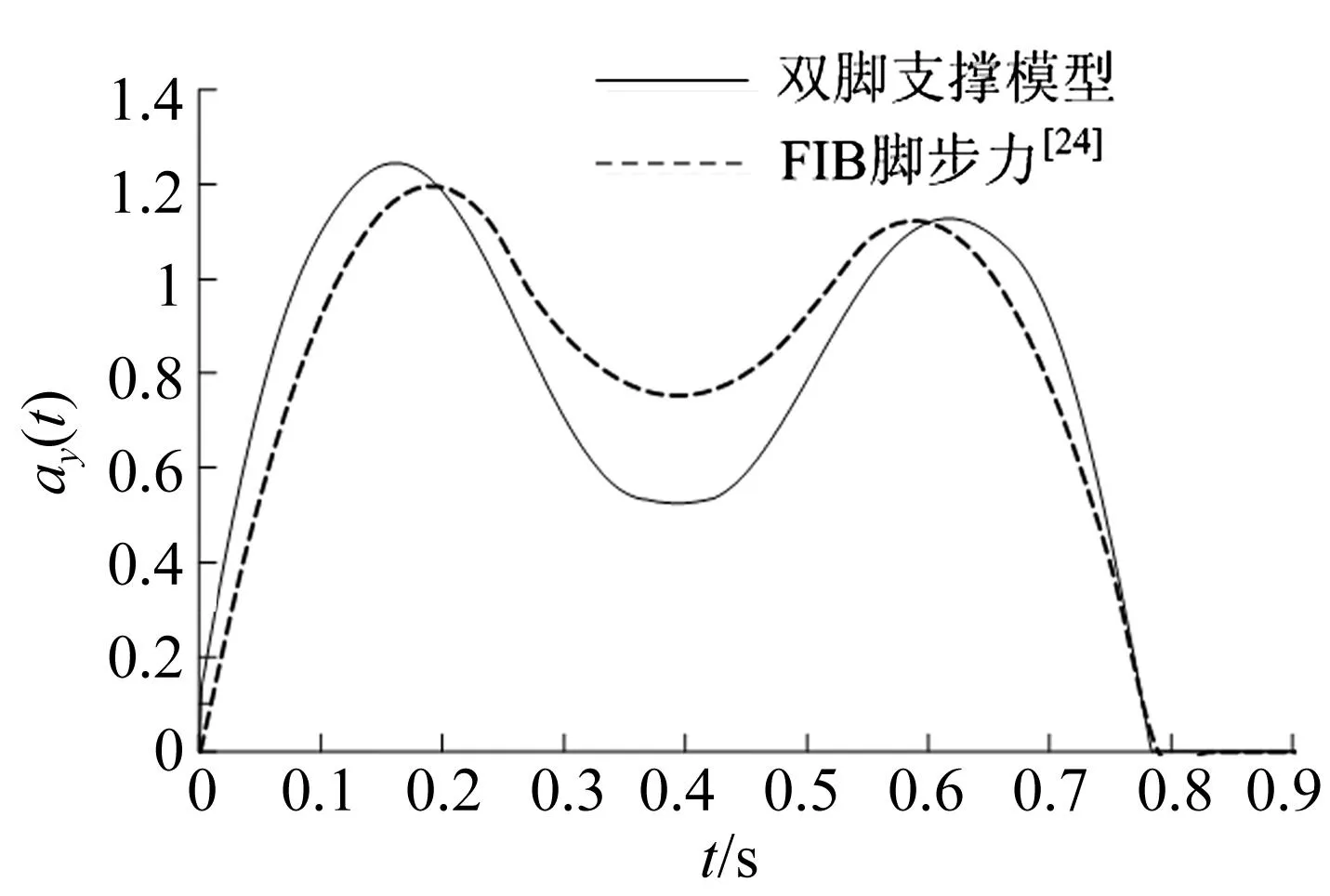
图6　步伐力模拟结果与文献[24]对比图Fig.6 Comparison of the simulated ground reaction force with the curve from reference [24]

图7为行人以1.5 Hz至2.0 Hz步频在刚性路面行走时的单脚步伐力时程曲线模拟结果。图7中，αy为竖向动荷载系数，αx为纵向动荷载系数，即

(8)

式中，Fy、Fx分别为竖向步伐力和纵向步伐力，G为人体重量。图中双峰特性随步频的变化规律与文献[24]基本一致，验证了本文提出的人桥耦合振动计算方法的合理性。

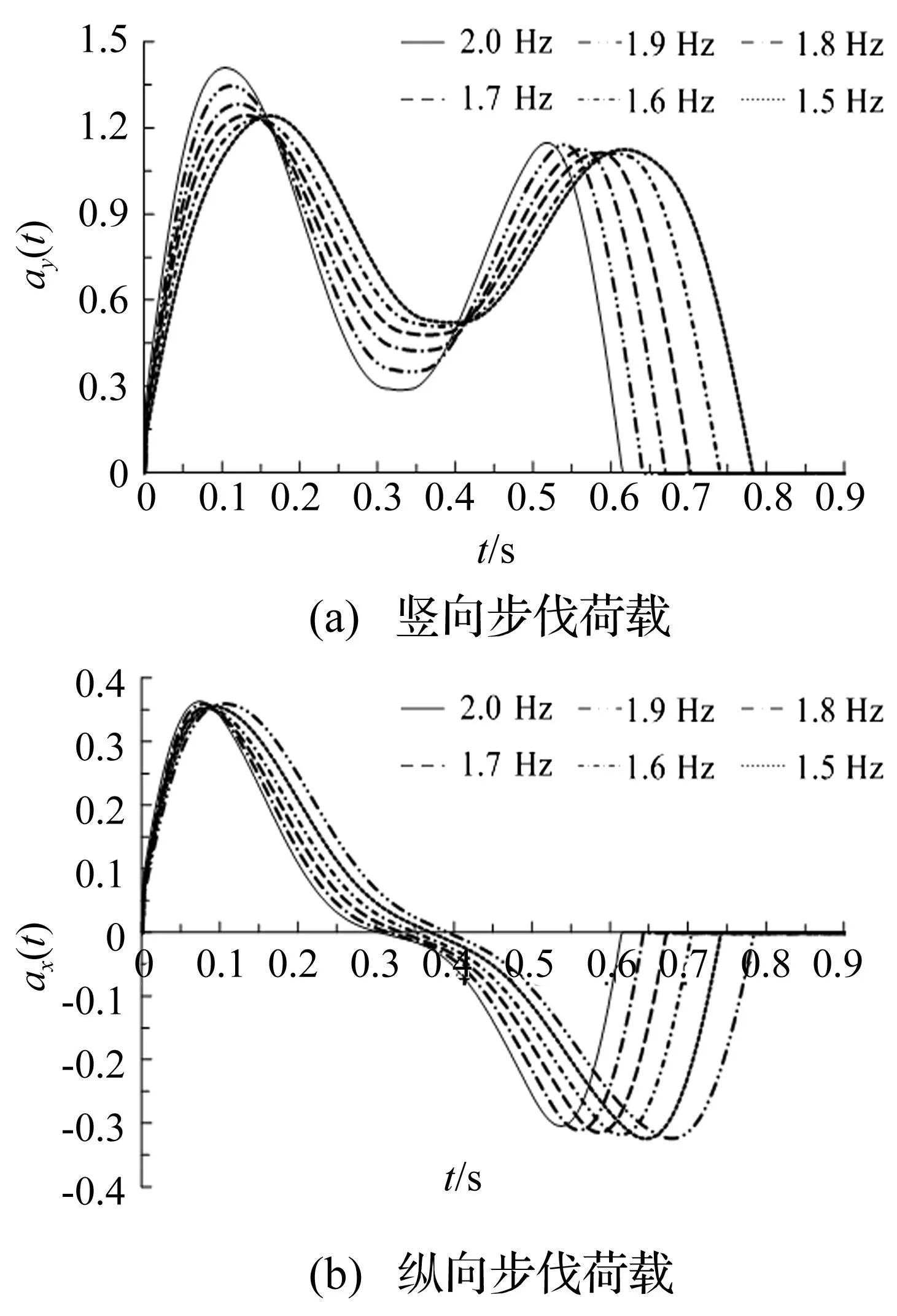
图7　不同频率行走的步伐荷载Fig.7 Ground reaction forces with different pacing frequencies

在上述人体计算模型中，相关参数主要包括前脚落地瞬间的重心位置λCOM、腿部刚度k和阻尼系数c。为了研究这些参数对步伐荷载的影响，本文对参数的取值进行比较分析。图8为当步频1.5 Hz时的计算结果。由图可知，脚步落地时，重心位置越靠前，腿部刚度越大，竖向力凹凸程度越大，反之越小。相比之下，腿部的阻尼取值对步伐力的影响较小。

根据上述对比分析，腿部刚度和阻尼比应在16 kN/m、0.14 kN.s/m左右取值，而λCOM随着步频增加逐渐增大，大致为0.50～0.60。

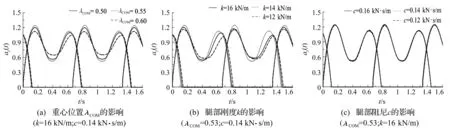
图8　重心位置，腿的刚度和阻尼对步伐荷载的影响Fig.8 Effect of the COM position, the leg stiffness and the leg damping on the shape of ground reaction force

1.3人-桥竖向耦合振动计算方程

本文利用有限元法进行结构动力计算，人-桥耦合振动方程如下：

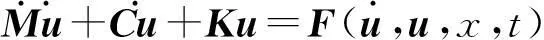
(9)

2铝合金人行桥竖向耦合振动分析

2.1桥梁概况

本文以杭州市复兴路铝合金人行天桥为例，基于上述竖向耦合振动计算模型，分析人-桥耦合振动对轻质人行桥动力响应的影响。该桥为上端开口的简支梁桁架桥，跨度为22.8 m，桥面宽度4.5 m。为了方便计算，采用空间单梁模型，按等刚度和等质量进行换算。桥梁的单位长度质量为491 kg/m，竖向弯曲变形的截面等效惯性矩为0.04 m4，侧向弯曲变形的截面等效惯性矩为0.093 m4，等效扭转常数为0.011 m4，弹性模量为7×107kN/m2。图9为人行桥的平面图与横断面图。

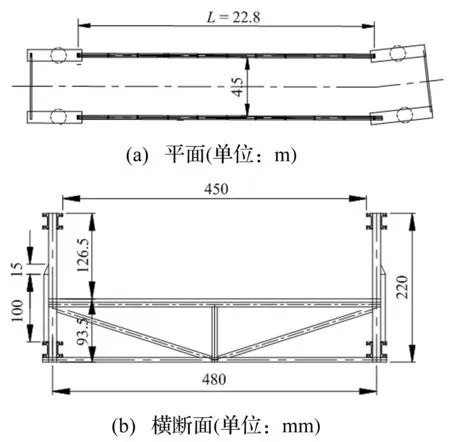
图9　铝合金人行桥Fig.9 Aluminum alloy footbridge

采用Rayleigh阻尼考虑结构阻尼效果，即：

C=α0M+β0K

(10)

式中，系数α0取0.02，β0取0.000 4，前三阶对应的阻尼比约为0.93%，1.40%，3.64%。

结构自振频率计算结果如表1所示，竖向振动的基频为7.23 Hz，远大于《城市人行天桥与人行地道技术规范》(CJJ69-95)规范规定的舒适性验算频率3.0 Hz。

2.2单人通行时的耦合振动计算

首先计算单人步行荷载下的桥梁振动响应。假定行人沿着桥梁的中心线走行，步频为1.8 Hz，步长为0.7 m，体重0.7 kN。桥梁跨中点作为结构振动响应输出点。

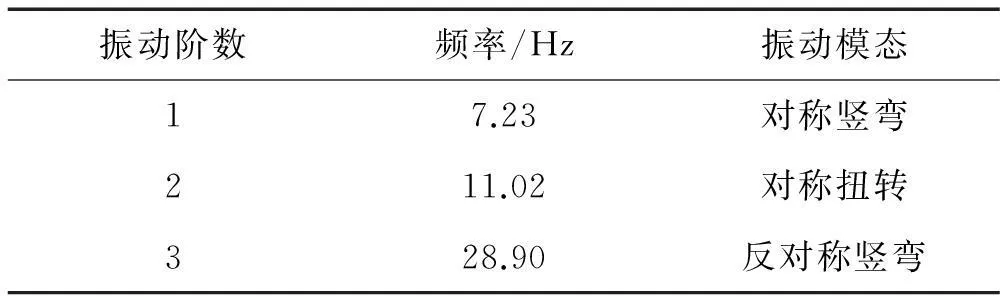
表1　铝合金人行桥的自振特性

图10为人体重心位置COM的竖向位移和速度时程曲线，表明行人在行走中能够保持稳定的动力过程。图11为桥梁跨中的竖向挠度、速度和加速度响应时程，分人-桥耦合和非耦合两种情况。结果表明，在单人通过时考虑耦合振动的结果与不考虑耦合振动的结果基本一致，耦合振动的影响较小。

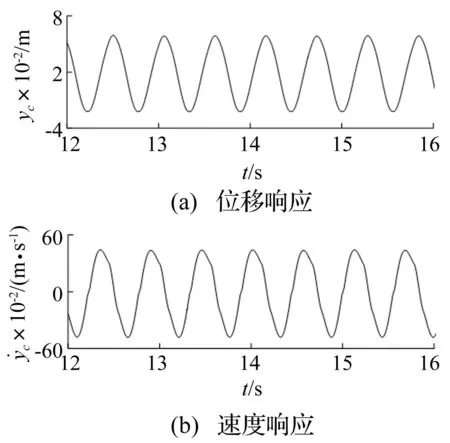
图10　重心(COM)的振动响应Fig.10 Dynamic responses of the COM in walking

2.3人群荷载下的耦合振动计算

为了模拟人行桥在实际运营状态时的振动响应，本文将上述单人模型运用于人群作用下的人-桥耦合振动响应计算。假定人群密度为0.2～3.0人/m2。为考虑人群个体的随机特性，将人群分布位置、步频、体重、腿长、步长等用Monte-Carlo法在设定的数据范围内随机生成。其中步频为1.6～1.8 Hz，体重为0.6～0.8 kN，人群在桥面均匀分布。走行方向跟据人在桥面的位置确定，即按照靠右行走规则根据人在桥面上的位置规定其前进方向。人群总数N根据人群密度计算得到，即为单位面积人数×桥面面积。在同一人群密度下用相同的人群分布条件分别计算考虑耦合振动和不考虑耦合振动的影响。另外，当行人步行出桥5 m以后在入桥位置激活刚出桥的行人，并按原速度步入桥梁，以确保桥面上的总人数保持不变，形成稳态的人群荷载模式。

为了获得更为可靠的动力响应结果，将每一种人群密度计算10个不同的随机人群工况，得到各人群密度下的竖向最大加速度均值。

表2为不同密度人群作用下考虑与不考虑人桥耦合振动的桥梁跨中最大竖向动力响应均值对比。表中“No”为不考虑人桥耦合的结果，“Yes”为考虑耦合的结果。作为一例,图12给出了三种人群密度情况下的

加速度响应时程及相应的FFT频谱分析对比图。图中，“Y”表示考虑耦合作用的结果，“N”表示不考虑耦合作用。结果表明，计算时是否考虑人-桥耦合作用，对铝合金人行天桥的动力响应结果有明显的影响，影响程度随着人群密度增大而变得更为显著；考虑人-桥耦合作用时，动力响应计算结果明显小于不考虑相互作用的计算结果。产生这一现象是因为考虑人桥耦合影响时，振动频率较为分散，不同频率的振动相互抵消。如图12所示，考虑人桥耦合影响时的结构振动含有多个卓越频率，而不考虑人桥耦合影响的振动响应卓越频率更为集中。

表2　不同密度的人群过桥时结构最大动力响应均值

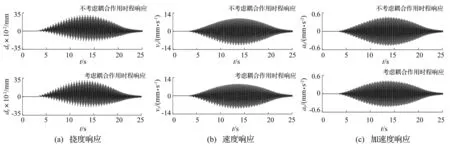
图11　单人过桥时结构跨中的振动响应时程Fig.11 Dynamic responses at midspan of footbridge with single pedestrian walking

图12　人群过桥时结构跨中加速度响应时程与FFT频谱Fig.12 Dynamic responses and FFT spectra at midspan point of footbridge with stochastic crowd excitation

3结论

本文建立了考虑人-桥竖向耦合振动的人行桥结构动力计算方法，并以一座跨度为22.8 m的简支铝合金人行天桥为例，分析了考虑与不考虑人桥耦合振动对轻质人行桥结构动力响应的影响。研究得到以下几点结论：

(1) 通过与文献的步伐荷载对比，验证了双脚支撑模型得到的步伐荷载能较好反应脚步力的基本特征。

(2) 通过比较分析不同人体参数条件下的步伐荷载计算结果，计算模型的腿部刚度和阻尼建议在16 kN/m、0.14 kN.s/m左右取值；脚步落地瞬间的人体重心位置距离前脚落地点为步长的0.50倍～0.60倍前后。

(3) 通过实际人行桥的人-桥耦合振动计算分析，验证了提出的人-桥耦合振动响应计算方法即使在高密度的随机人群工况下，结构动力计算也具有较好的收敛性和稳定性。

(4) 铝合金人行天桥由于自重轻，采用不考虑人桥耦合影响的计算方法得到的结果偏大。

参 考 文 献

[ 1 ] 程晓东. 新型铝合金结构在城市人行天桥中的应用[J]. 桥梁建设, 2007 (6): 38-41.

CHENG Xiao-dong. Application of new type ofaluminum alloy structure to urban pedestrian overpass[J]. Bridge Construction, 2007 (6): 38-41.

[ 2 ] 中华人民共和国建设部. CJJ69-95. 城市人行天桥与人行地道技术规范[S]. 北京：中国建筑工业出版社，1996.

[ 3 ] Hivoss(Human induced vibration of steel structure).EN03-2007. Design of footbridges [S]. Germany: 2008.

[ 4 ] Stetra, Technical guide footbridges-Assessment of vibrational behavior of footbridges under pedestrian loading [S]. Paris: Technical Guide, 2006.

[ 5 ] British Standards Association. BS 5400. Steel, Concrete and Composite Bridge-Part 2: Specification for Loads [S]. London: British Standards Association, 1978.

[ 7 ] Blanchard J, Davies B L, Smith J W. Design criteria and analysis for dynamic loading of footbridges[C]. In: Symposium on Dynamic Behavior of Bridges, eds. Proceeding of Symposium on Dynamic Behaviour of Bridge. Crowthorne: Transport and Road Research Laboratory, 1977. 90-100.

[ 8 ] Bachmann H, Ammann W. Vibrations in structures: induced by man and machines[M].Zurich: IABSE-AIPC-IVBH, 1987:13-43.

[ 9 ] Ohlsson S V. Floor vibrations and human discomfort[D]. Goteborg: Chalmers University of Technology, Division of Steel and Timber Structures, 1982.

[11] Venuti F, Bruno L. Crowd-structure interaction in lively footbridges under synchronous lateral excitation: A literature review[J]. Physics of Life Reviews, 2009, 6(3): 176-206.

[12] Bocian M, Macdonald J H G, Burn J F. Biomechanically inspired modelling of pedestrian-induced forces on laterally oscillating structures[J]. Journal of Sound and Vibration, 2012, 331(16): 3914-3929.

[13] 法永生, 李东, 孙翠华. 人行桥随机人行荷载下的振动分析及其舒适度评价的新方法[J]. 振动与冲击, 2008, 27(1): 119-123.

FA Yong-sheng, LI Dong, SUN Cui-hua. Vibration analysis for a footbridge under stochastic pedestrian load and a new method for comfort evaluation[J]. Journal of Vibration and Shock, 2008, 27(1): 119-123.

[14] 李红利, 陈政清. 考虑荷载随机性的人行桥人致振动计算方法研究[J]. 湖南大学学报: 自然科学版, 2013, 40(10): 22-31.

LI Hong-li, CHEN Zheng-qing. A calculation method for footbridge vibration under stochastic pedestrian loading[J]. Journal of Hunan University:Natural Sciences, 2013, 40(10): 22-31.

[15] Racic V, Pavic A, Brownjohn J M W. Experimental identification and analytical modelling of human walking forces: literature review [J]. Journal of Sound and Vibration, 2009, 326(1): 1-49.

[16] Dallard P, Fitzpatrick A J, Flint A, et al. The London millennium footbridge[J]. Structural Engineer, 2001, 79(22): 17-21.

[17] Ingolfsson E T, Georgakis C T, Ricciardelli F, et al. Experimental identification of pedestrian-induced lateral forces on footbridges [J]. Journal of Sound and Vibration, 2011, 330(6): 1265-1284.

[18] 袁旭斌. 人行桥人致振动特性研究[D]. 上海：同济大学，2006.

[19] 宋志刚，张尧. 人-桥侧向动力相互作用下的动力放大系数分析[J].振动与冲击,2015,34(1):19-23.

SONG Zhi-gang, ZHANG Yao. Analysis of the dynamic amplification factor of lateral structural vibration induced by crowd-bridge interaction[J]. Journal of Vibration and Shock, 2015, 34(1): 19-23.

[20] Sachse R, Pavic A, Reynolds P. Human-structure dynamic interaction in civil engineering dynamics: A literature review [J]. Shock and Vibration Digest, 2003, 35(1): 3-18.

[21] Ellis B R. Human-structure interaction in vertical vibrations [J]. Proceedings of the ICE-Structures and Buildings, 1997, 122(1): 1-9.

[22] 李红利, 陈政清. 人-桥竖向动力相互作用效应理论与试验研究[J]. 土木工程学报, 2014, 47(6): 78-87.

LI Hong-li, CHEN Zheng-qing. Analytical and experimental study on vertically dynamic interaction between human and bridge[J]. China Civil Engineering Journal, 2014, 47(6): 78-87.

[23] Qin J W, Law S S, Yang Q S, et al. Pedestrian-bridge dynamic interaction, including human participation [J]. Journal of Sound and Vibration, 2013, 332(4): 1107-1124.

[24] International Federation for Structural Concrete, Task Group 1.2. Guidelines for the Design of Footbridges: Guide to Good Practice[M]. Switzerland: fib, 2005. 30.

[25] Whittington B R, Thelen D G. A simple mass-spring model with roller feet can induce the ground reactions observed in human walking [J]. Journal of Biomechanical Engineering, 2009, 131(1): 011013.

[26] Geyer H, Seyfarth A, Blickhan R. Compliant leg behavior explains basic dynamics of walking and running[J]. Proceedings of the Royal Society B: Biological Sciences, 2006, 273(1603): 2861-2867.

Calculation method for human-bridge vertically coupled vibration

XIEXu,ZHONGJing-ru,ZHANGHe,ZHANGZhi-cheng(Department of Civil Engineering, Zhejiang University, Hangzhou 310058, China)

Abstract:In order to investigate the human-bridge vertically coupled vibration of lightweight footbridges, a human-bridge vertically coupled vibration equitation based on a bipedal pedestrian model was developed. A comparison between the simulated foot force on rigid ground and the foot force time history curve presented in reference showed that the human body bipedal walking model provided here can simulate the features of ground reaction force properly. Reasonable ranges of the parameters of this bipedal model were discussed. A 22.8m-span aluminum alloy footbridge (with the 1st vertical bending vibration natural frequency of 7.23 Hz) was taken as an example to calculate the structural dynamic responses under vertical crowd-bridge interaction. Stochastic crowd walking parameters were generated by Monte-Carlo method to simulate the random crowd conditions of different densities, and the direct integral method was used to compute the dynamic response of the foot bridge considering crowd-bridge vertically coupled vibration. The results indicated that as the crowd density rises, the predominant frequencies of the human-bridge coupled vibration tend to dispersing, the vibration responses are much smaller than those not considering the coupling effect.

Key words:footbridge; coupled vibration; serviceability; foot force; stochastic crowd

中图分类号:U448.11

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.05.017

收稿日期：2014-11-21修改稿收到日期：2015-03-12

基金项目：国家自然科学基金资助项目(51378460)

第一作者 谢旭 男，博士,教授，1963年12月生