试分析复杂表面多轴数控加工的精度控制
2016-04-21王炜罡长春汽车工业高等专科学校长春130013
王炜罡(长春汽车工业高等专科学校,长春 130013)
试分析复杂表面多轴数控加工的精度控制
王炜罡
(长春汽车工业高等专科学校,长春130013)
摘 要:本文在简单分析影响该过程加工精度原因的基础上,还分别研究了加工误差的自适应补偿方法和该过程加工精度的模型构建,以期为广大数控加工工作者提供一定的参考依据。
关键词:复杂表面;多轴数控加工;自适应补偿方法;模型构建
0 引言
随着科学技术的不断发展和进步,数控加工技术也得到了长足的发展,尤其是针对复杂表面的加工技术,其精度控制要求越来越严格。在传统方法中,针对复杂表面的加工需要根据不同的工序在不同的设备上进行。现在利用多轴数控加工之后,较之以前有了很大的改进,这一步骤的省略,不仅节省了大量的作业时间,还在大幅度提升作业效率的基础上,同步提升了加工精度。
1 复杂表面中多轴数控加工误差的影响因子
(1)铣削加工误差。从本质上分析,数控机床的加工其实就是简单的插补,即在将所需加工的曲线分割为细小的多个部分后,用直线插补或圆弧插补等基本现行进行加工曲线和曲面的拟合。在进行加工之前,需要根据零件图纸,获得相应的几何信息和工艺信息,从而编写出对应的加工程序。然后,将已编写完成的加工程序导入数控机床,经由相应的数控装置进行相应动作的机床主运动控制。通常情况下,这些动作包括变速、停止、启动、速度与位移量等。由于曲面加工时,对不同曲面要求的精度不同,所以在实际加工中,会将其进行离散处理,使其成为一系列不同的微平面。又由于加工过程中存在于各个曲面的点都具有相应的法矢量,且法矢量始终处于变化状态,所以,刀轴适量也会随之不断变化,致使道具的接触点轨迹与先前离散的曲线线段不吻合,从而导致大量误差产生。
(2)系统累积误差。在复杂表面的整个加工过程中,影响其加工精度的原因和误差来源很多。不仅包括工艺系统的客观精度、机床运动的客观精度、热力变形因素、数控加工的编程技术以及工艺系统的客观振动等客观因素,还包括道具类型、进退刀方式和起刀点、走刀方式以及切削容差和间距等误差来源。当这些因素一直累积并达到某一临界点时,就会严重影响整个拟加工零件的表面质量。所以,想要加工精度满足客观要求,就需要尽可能地避免或减少误差累积。
2 自适应补偿加工精度误差的具体方法及其算法
(1)自适应补偿法。针对加工误差的补偿而言,其真正的实现方法是通过插补。根据导入的已知零件程序信息,数控装置将程序段描述中介于曲线终点和起点的空间进行数据密化处理,从而实现既定的轮廓轨迹。对较为复杂的形状来讲,如果直接对其进行算法直接生成,则会变得更加复杂,计算机的工作量也会随之大幅度增加。然而,在多轴的数控加工中,其产生的插补误差具备非线性质,对其进行误差减小处理时,就可以应用线性加密、自适应刀位点等方法。在具体的加工过程中,为了充分保证产生误差在公差允许的范围之内,可以利用刀位点的自适应补偿法,使得刀位点的密化处理相对简单化。
(2)自适应补偿算法。以五轴的数控铣床为研究对象,对其进行补偿算法的分析和计算。假设刀位数据(pw0,uw0)和(pw1,uw1)是相邻的,且(X0,Y0,Z0,A0,B0)是与前者对应的各联动控制轴的具体运动位置,(X1,Y1,Z1,A1,B1)是与后者对应的各联动控制轴的具体运动位置。
由此可以得出:各轴的具体运动是X(t)=X0+t(X1-X0),Y(t)=Y0+t(Y1-Y0), Z(t)=Z0+t(Z1-Z0), A(t)=A0+t(A1-A0),B(t)=B0+t(B1-B0)。其中,。
w的距离为对上述式子进行t求导,即可得到误差的最大值。如果该值大于允许值,则应该在两到位点进行中点刀位插补。然后按照上述方法进行二次误差校验,直至误差值在精度允许范围内。
3 复杂表面多轴数控加工精度的模型构建分析
图1为球头铣刀螺旋刃的几何模型图。以此为例,进行数控加工精度的建模分析。

图1 球头铣刀模型示意图
球面的方程坐标为:
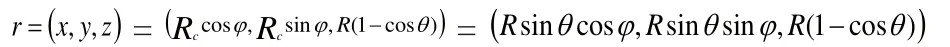
上式中,R表示铣刀球刃的半径,q表示道具轴线与球心和刀刃点连线的夹角,j表示螺旋滞后的角度,P表示螺旋曲面的导程,Rc表示道具轴线与刀刃点的中间距离。分析等距离螺旋曲面和球面的交线,可以得到铣刀刃线的实际方程,即联立上述方程可得:=。由于,所以。由此可得,当cosq为0时,有最大值。故此,球头铣刀刃线的最终方程为:
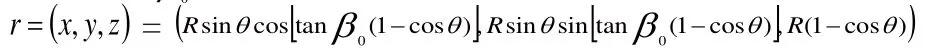
4 应用实例分析
为了便于自适应补偿加工前后误差对比,作者进行了两组实验。将曲面截面设为正弦曲线,对其进行相应刀具路径的规划,并同步确定其相关切削参数。针对第一组实验,使用制造工程师CAXA中的NC代码。针对第二组实验,使用自适应补偿后重写的NC代码。
5 结束语
综上所述,在复杂表面的数控加工过程中,影响其加工精度的因素很多,其中编程误差的影响相对较大。通过实践证明,利用自适应补偿及其算法的分析计算,可以充分控制其误差使其符合要求精度。除此之外,通过建立模型的方式,计算其相应的刃线方程,从而控制整个系统加工的精度,也是非常有效的。
参考文献:
[1]刘怡飞.基于复杂曲面的多轴数控加工非线性误差的控制研究[J].科技与创新,2015(01):73-74.
作者简介:王炜罡(1969-),男,吉林长春人,本科,助教,高级技师,研究方向:数控加工工艺、CAD技术应用。
DOI:10.16640/j.cnki.37-1222/t.2016.03.023
