基于细菌觅食算法的砂砾岩岩性识别方法

王飞+边会媛+韩雪+张意+张永浩

摘要：砂砾岩储层岩性复杂多变，母岩成分变化大，孔隙结构复杂，难以精确划分岩性并建立准确的解释模型，导致储层参数计算精度不高。针对松辽盆地梨树断陷砂砾岩储层特点，选择多组分体积模型作为该地区的测井解释模型，将该地层看成由局部均匀的孔隙、泥质、石英、长石、岩屑等5部分组成。根据多组分体积模型建立相应的测井响应方程，引入细菌觅食算法作多组分矿物模型的优化算法，将优化结果与岩芯分析孔隙度及全岩矿物分析的体积分数进行对比，结果验证了细菌觅食算法反演砂砾岩储层多组分矿物模型的可靠性。采用该方法对松辽盆地砂砾岩储层测井资料进行处理，取得了较好的结果。

关键词：测井解释；砂砾岩；细菌觅食算法；多组分矿物模型；最优化反演；岩性；孔隙度；松辽盆地

中图分类号：P618.130.2；TE122文献标志码：A

Identification Method of Sandyconglomerate Lithology Based on Bacterial Foraging Algorithm

WANG Fei1， BIAN Huiyuan2， HAN Xue3， ZHANG Yi3， ZHANG Yonghao4

（1. School of Geology Engineering and Geomatics， Changan University， Xian 710054， Shaanxi， China；

2. College of Geology and Environment， Xian University of Science and Technology， Xian 710054，

Shaanxi， China； 3. The First Branch of the Logging Company， Shengli Petroleum Engineering Co. Ltd.，

Dongying 257200， Shandong， China； 4. CNPC Logging Co. Ltd.， Xian 710077， Shaanxi， China

）

Abstract： Sandyconglomerate reservoir lithology is complex， composition variation of parent rock is large， pore structure is complex and strong heterogeneity， so that it is difficult to accurately divide lithology and build accurate interpretation model， resulting in low reservoir parameter calculation accuracy. Based on the characteristics of sandyconglomerate reservoir in Lishu fault of Songliao Basin， a multicomponent volume model was established for well logging interpretation， and the stratum was taken as the combination of local homogeneous pore， muddy， quartz， feldspar and rock debris. According to the multicomponent volume model， the corresponding log response equation was built， and the bacterial foraging algorithm was taken as the optimal solution of multicomponent mineral model， and then the optimized results were compared with the porosity by core analysis and the volume fraction by wholerock mineral analysis. The results verify that the bacteria foraging algorithm is reliable for the inversion of sandyconglomerate multicomponent mineral model. Based on bacteria foraging algorithm， the result is good for the well logging interpretation of sandyconglomerate reservoir in Songliao Basin.

Key words： well logging interpretaton； sandyconglomerate； bacterial foraging algorithm； multicomponent mineral model； optimization inversion； lithology； porosity； Songliao Basin

0引言

砂砾岩储层岩性复杂多变，储层岩石矿物主要成分包括石英、长石和岩屑。部分长石和岩屑具有放射性，对利用自然伽马测井计算泥质体积产生干扰，因此，充分考虑砂砾岩岩性，合理建立测井响应方程，准确求取各组分体积分数，可以提高砂砾岩储层地质参数的评价精度。国内外研究的思路是加强对砂砾岩岩性的分析，采用的方法为最优化测井解释方法[18]。

近年来，随着对非线性反演领域的重视，已经出现了一大批具有巨大潜力和应用价值的非线性反演方法，并应用于测井最优化解释领域。这些算法原理各不相同，有以数学为基础的蒙特卡洛法、最速下降法、拟牛顿法等，这些方法都存在计算复杂和收敛速度方面的问题。有基于仿生原理的遗传算法等，这种算法已经广泛应用于测井最优化反演，并取得了很好的效果，但是容易过早收敛，且当连续性条件严格时，搜索效率下降。随着信息处理技术的发展，群体智能优化算法成为解决多参数、非线性最优化的有效手段，典型的群体智能算法有蚁群算法、粒子群算法、细菌觅食算法等，这些算法在石油地球物理勘探领域的应用越来越广泛[912]。

细菌觅食算法是Passino于2002年提出的一种新型仿生类群体智能算法，主要依靠以细菌特有的趋化、繁殖、迁徙3种行为为基础的3种算子进行位置更新和最优解的搜索，进而实现种群的进化[1317]。本文将细菌觅食算法引入到最优化测井解释中，并应用于砂砾岩储层评价。

1最优化测井解释模型的建立

1.1最优化测井解释基本原理

最优化测井解释是根据地球物理学广义反演理论，以反映地层特征的实际测井值ai为基础，根据储层地质和孔隙结构等特征建立适当的解释模型并选择多种测井响应方程，合理选择区域性解释参数与储层参数初始值，使反演结果充分逼近实际测井值，目标函数值达到最小。

应用最优化方法进行测井解释的优化数学模型可归结为

min F（x，ai）=min∑mi=1（ai-fi（x，z））2σ2i+τ2i

s.t. hk（x）=0，k=1，2，…q

gj（x）≥0，j=1，2，…p（1）

式中：F（x，ai）为测井解释的目标函数；fi（x，z）为第i种测井响应函数；x为未知储层参数向量；z为区域性解释参数向量；m为测井曲线个数；σi为第i种测井值的测量误差；τi为第i种测井值的响应方程误差；gj（x）为不等式约束；hk（x）为等式约束；q为不等式个数；p为等式个数。

1.2砂砾岩储层岩石矿物组分分析

松辽盆地梨树断陷砂砾岩储层岩性复杂，对梨树断陷岩矿数据进行统计，结果表明砂砾岩储层岩石矿物主要成分为岩屑、石英和长石。其中，岩屑主要包括中、酸性喷出岩以及少量的碎裂岩和变质岩。

1.3砂砾岩多组分体积模型及目标函数

为简化模型，将钾长石和斜长石作为一个整体，地层由孔隙、泥质、石英、长石和岩屑5个组分组成（图1）。

2细菌觅食算法基本原理及最优化测井解释流程

2002年Passino提出的细菌觅食算法是一种新型仿生类群体智能算法，以趋化、繁殖、迁徙3种行为为基础的3种算子进行位置更新和最优解的搜索，进而实现种群的进化。细菌觅食算法具有全局性、快速性、高精度和能源占用低等特点。

细菌觅食算法包括3个主要的算子，即趋化算子、繁殖算子和迁徙算子。这3个算子是算法的核心思想，并且决定算法的性能。

2.1趋化（Chemotaxis）

趋化是细菌朝着营养丰富充足的地方聚拢的运动过程。细菌在趋化进程内运动方式由前进（Swim）和翻转（Tumble）组成。翻转即为细菌朝着任意的方向前进单位的步长。

2.2聚集（Swarming）

在菌群寻取食物的过程中，细菌个体之间通过相互间的作用达到群体的聚集行为。细胞与细胞之间存在引力，又存在斥力。引力使细菌聚集在一起，甚至出现“抱团”现象；斥力使每个细菌都有一定的位置，使其能在该位置上获取能量，以维持生存。

2.3繁殖（Reproduction）

经过一定的趋化步骤后，觅食结果较好的细菌进行繁殖，通过细胞分裂生成与父代完全相同的子代，没有繁殖的细菌将死掉，以此维持菌群的规模不变。繁殖是一个拣选的过程，通过健康度函数选择出进化繁殖的细菌。

2.4迁徙（Elimination and Dispersal）

细菌生活的区域可能会突然发生剧烈变化，也有可能突然受到其他影响。迁徙指实际环境中的细菌被外力杀死或者驱散到新的区域中去，这破坏了细菌的趋化过程，但是细菌也可能寻找到食物更为丰富的区域，因此，从长远来看，这更有利于趋化算子跳出局部最优解和寻找全局最优解。

2.5细菌觅食算法最优化测井解释流程

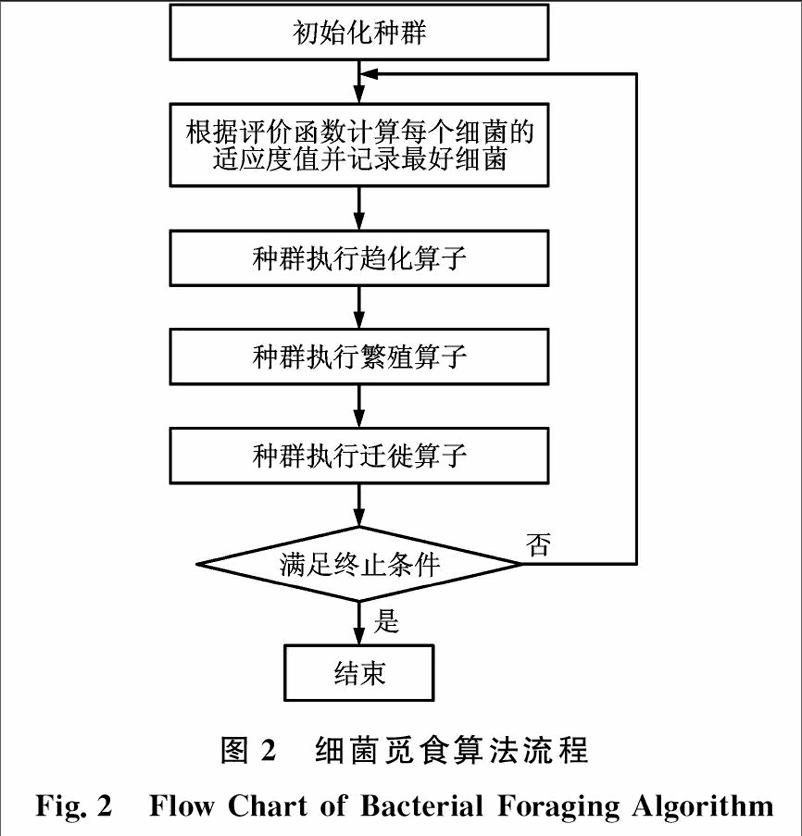
细菌觅食算法求解最优化问题的具体步骤有5个部分（图2）。随机初始化种群，设置种群的大小为500，聚类数目为5，趋化次数为50，趋化操作中单向运动的最大步数为4，每个细菌的迁移概率为0.25，执行种群的趋化、繁殖、迁徙操作，判断新位置的适应度值是否更好。如果更好，将新位置的适应度值存储为细菌目前最好的适应度值；如果不是，返回重新计算新位置上的适应度值，直到满足全局最优适应度值，最后输出结果。

4应用实例及效果分析

表2为松辽盆地A井2 515～2 530 m深度段反演的各组分体积分数与岩芯分析结果误差对比。由表2可见：计算的孔隙度与岩芯分析数据相比，平均绝对误差为0.016，平均相对误差为0275；计算的石英体积与岩芯分析数据相比，平均绝对误差为0.051，平均相对误差为0.196；计算的长石体积与岩芯分析数据相比，平均绝对误差为0.087，平均相对误差为0269；计算的岩屑体积与岩芯分析数据相比，平均绝对误差为0.044，平均相对误差为0160。图3为A井2 515～2 530 m深度段细菌觅食算法反演结果。由误差分析可知，重构理论曲线与实际测井曲线平均绝对误差与平均相对误差均较小，说明反演结果是正确的。

图4为A井2 515～2 530 m深度段重构曲线与实际测井曲线质量检测结果。表3为重构曲线理论值与实际测井曲线误差分析结果。由表3可见：重构补偿中子孔隙度曲线与实际补偿中子孔隙度测井值相比，平均绝对误差为1.410，平均相对误差为0.143；重构密度曲线与实际密度测井值相比，平均绝对误差为0014，平均相对误差为0.006；重构声波时差曲线与实际声波时差测井值相比，平均绝对误差为10660，平均相对误差为0.048；重构自然伽马与实际自然伽马相比，平均绝对误差为3.550，平均相对误差为0.038。由误差分析可知，重构理论曲线与实际测井值平均绝对误差与平均相对误差均较小，说明反演结果是正确的。

图5为松辽盆地B井1 330～1 350 m深度段细菌觅食算法反演结果。表2为B井反演的各部分体积分数与岩芯分析数据误差对比结果，B井只分析了岩芯孔隙度。由表2可见，计算的孔隙度与岩芯分析数据相比，平均绝对误差为0.017，平均相对误差为0.194。

图6为B井1 330～1 350 m深度段重构曲线与实际测井曲线质量检测结果。重构曲线理论值与实际测井曲线误差分析结果见表3。由表3可见：重构补偿中子孔隙度曲线与实际补偿中子孔隙度测井值相比，平均绝对误差为2.030，平均相对误差为0.125；重构密度曲线与实际密度测井值相比，平均绝对误差为0033，平均相对误差为0012；重构声波时差曲线与实际声波时差测井值相比，平均绝对误差为26970，平均相对误差为0.096；重构自然伽马曲线与实际自然伽马测井值相比，平均绝对误差为7580，平均相对误差为0.097。由误差分析可知，B井中该方法反演结果也有效。

5结语

（1）砂砾岩储层岩性复杂，岩石矿物包括石英、长石和岩屑，并且岩屑的成分比较复杂。合理建立多组分矿物模型并确定反演目标函数，综合利用多种常规测井曲线信息，设置合理的约束条件，利用细菌觅食算法可以获取非线性多组分矿物模型的最优解。

（2）将细菌觅食算法应用于松辽盆地砂砾岩储层多组分矿物模型解释中，模型反演效果稳定可靠，应用效果较好。

（3）由于细菌觅食算法是一种新型的基于群体的优化工具，虽然具有取得全局最优解的能力，但其研究仍然处于起步阶段，所以该算法的理论基础及工程应用仍需进一步研究和推广。

参考文献：

References：

[1]韩雪，潘保芝，张意，等.遗传最优化算法在砂砾岩储层测井评价中的应用[J].测井技术，2012，36（4）：392396.

HAN Xue，PAN Baozhi，ZHANG Yi，et al.GAoptimal Log Interpretation Applied in Glutenite Reservoir Evaluation[J].Well Logging Technology，2012，36（4）：392396.

[2]田云英，夏宏泉.基于多矿物模型分析的最优化测井解释[J].西南石油学院学报，2006，28（4）：811.

TIAN Yunying，XIA Hongquan.The Optimal Logging Explantion Base on Multim in Erals Model Analysis[J].Journal of Southwest Petroleum Institute，2006，28（4）：811.

[3]段亚男，潘保芝，韩雪.砂砾岩储层的多组分模型及最优化测井解释[J].国外测井技术，2012，33（6）：2023.

DUAN Yanan，PAN Baozhi，HAN Xue.Multicomponent Model and Optimization Logging Evaluation of Glutinite Reservoirs[J].Word Well Logging Technology，2012，33（6）：2023.

[4]申本科，赵红兵，崔文富，等.砂砾岩储层测井评价研究[J].地球物理学进展，2012，27（3）：10511058.

SHEN Benke，ZHAO Hongbing，CUI Wenfu，et al.Sandy Conglomerate Reservoir Logging Evaluation Study[J].Progress in Geophysics，2012，27（3）：10511058.

[5]陈钢花，王有涛，董维武，等.深层砂砾岩储层测井精细评价[J].海洋石油，2010，30（2）：8286.

CHEN Ganghua，WANG Youtao，DONG Weiwu，et al.Fine Evaluation on Deep Glutenite Reservoirs with Well Logging Data[J].Offshore Oil，2010，30（2）：8286.

[6]熊杰，刘彩云，邹长春.基于粒子群优化算法的感应测井反演[J].物探与化探，2013，37（6）：11411145.

XIONG Jie，LIU Caiyun，ZOU Changchun.The Induction Logging Inversion Based on Particle Swarm Optimization[J].Geophysical and Geochemical Exploration，2013，37（6）：11411145.

[7]刘倩茹，薛林福，潘保芝，等.梨树断陷砂砾岩测井岩性识别[J].测井技术，2013，37（3）：269273.

LIU Qianru，XUE Linfu，PAN Baozhi，et al.Study on Glutenite Reservoir Lithology Identification in Lishu Fault[J].Well Logging Technology，2013，37（3）：269273.

[8]边会媛，王飞，岳崇旺，等.利用弹性参数识别致密砂岩储层流体性质[J].地球科学与环境学报，2014，36（4）：99106.

BIAN Huiyuan，WANG Fei，YUE Chongwang，et al.Fluid Property of Tight Sandstone Reservoir Identified with Elastic Parameters[J].Journal of Earth Sciences and Environment，2014，36（4）：99106.

[9]邹长春，尉中良，柴细元，等.利用遗传算法实现最优化测井解释[J].测井技术，1999，23（5）：361365.

ZOU Changchun，WEI Zhongliang，CHAI Xiyuan，et al.Optimization of Log Interpretation Using Genetic Algorithm[J].Well Logging Technology，1999，23（5）：361365.

[10]徐志成，王树青.基于菌群优化算法的非线性系统模型参数辨识[J].计算机工程与应用，2013，49（1）：4649.

XU Zhicheng，WANG Shuqing.Parameter Identification of Nonlinear System Model Based on Bacterial Swarm Foraging for Optimization[J].Computer Engineering and Applications，2013，49（1）：4649.

[11]孟令群，郭建青.利用混沌粒子群算法确定河流水质模型参数[J].地球科学与环境学报，2009，31（2）：169172.

MENG Lingqun，GUO Jianqing.Application of Chaos Particle Swarm Optimization Algorithm to Determination of Water Quality Parameter of River Steam[J].Journal of Earth Sciences and Environment，2009，31（2）：169172.

[12]姜建国，周佳薇，郑迎春，等.一种自适应细菌觅食优化算法[J].西安电子科技大学学报：自然科学版，2015，42（1）：7581.

JIANG Jianguo，ZHOU Jiawei，ZHENG Yingchun，et al.Adaptive Bacterial Foraging Optimization Algorithm[J].Journal of Xidian University：Nature Science Edition，2015，42（1）：7581.

[13]周雅兰.细菌觅食优化算法的研究与应用[J].计算机工程与应用，2010，46（20）：1621.

ZHOU Yalan.Research and Application on Bacteria Foraging Optimization Algorithm[J].Computer Engineering and Applications，2010，46（20）：1621.

[14]杨尚君，王社伟，陶军，等.基于混合细菌觅食算法的多目标优化方法[J].计算机仿真，2012，29（6）：218222.

YANG Shangjun，WANG Shewei，TAO Jun，et al.Multiobjective Optimization Method Based on Hybrid Swarm Intelligence Algorithm[J].Computer Simulation，2012，29（6）：218222.

[15]李博.细菌觅食优化算法研究及其在图像检索中的应用[D].西安：西安电子科技大学，2014.

LI Bo.Research on Bacterial Foraging Optimization Algorithm and Its Application in Image Retrieval[D].Xian：Xidian University，2014.

[16]吉佳红，高尚.基于正交试验的细菌觅食算法的全局最优化[J].电子设计工程，2015，23（12）：2830.

JI Jiahong，GAO Shang.An Bacterial Foraging Algorithm Based on Orthogonal Experimental Method for Global Optimization[J].Electronic Design Engineering，2015，23（12）：2830.

[17]段亚男.苏里格致密砂岩储层 BFACM 混合最优化测井解释方法研究[D].长春：吉林大学，2015.

DUAN Yanan.Research on BFACM Hybrid Optimization Log Interpretation Method in Sandstone Reservoirs of Sulige Area[D].Changchun：Jilin University，2015.