具有多个受限制可用时间段的单机供应链排序问题

范静(上海第二工业大学理学院,上海201209)



具有多个受限制可用时间段的单机供应链排序问题

范静
(上海第二工业大学理学院,上海201209)

摘要:在文中所研究的单机供应链排序问题中,机器可用时间段的长度不大于给定常数,且每个不可用时间段长度确定。工件仅可以在机器的可用时间段内被加工,完工后可与其他完工工件组成一批,由一个容量无限制的运输工具发送给客户。运输工具在机器的每个可用时间段结束时间进行发送,且每次发送的费用固定。问题的目标是安排工件的加工、发送,以及机器的不可用时间段,以使总发送时间与总发送费用之和达到最小。对于工件允许中断的情况,可在多项式时间O(nlogn)内得到最优序(n为工件的个数)。对于工件不允许中断的情况,证明了问题是强NP-难的,并提出了2-近似算法。

关键词:可用时间段;供应链排序;强NP-难;近似算法

0　引言

供应链排序是把生产、分批和发送三者集成在一起,研究集成优化的模型及其算法[1]。实际上,供应链排序就是在排序决策范畴内研究供应链管理,是排序论在供应链管理中的应用。供应链排序的第一篇论文是由Potts[2]于1980年发表的。2003年Hall和Potts[3]在论文中系统地提出了供应链排序模型。此后,学者们对于供应链排序问题的研究就越来越多了。本文研究的是两阶段供应链排序问题,即工件在机器上加工后由运输工具,如卡车、轮船等,从工厂出发运输给客户。由于运输任务往往是由第三方物流公司负责的,所以可以认为运输工具的数量无限制,但会产生一定的运输费用。对于最小化总发送时间与总发送费用之和的目标,当运输工具容量无限制时,Hall等[3]给出了时间复杂度为O(n2)的最优动态规划算法(n为工件的个数);当运输工具容量有限制时,Chen和Vairaktarakis[4]给出了多项式时间为O(nlogn + nc)的最优动态规划算法,其中c表示运输工具的容量。

在大多数供应链排序问题的研究中,机器一直是可用的。但在实际的工作生产中,机器需要定期检修保养,以保证其生产质量,因而会出现多个不可用时间段。对于机器的可用时间段长度确定的情况,Chen[5]研究了目标为最小化完工时间和的问题,给出一个启发式算法及分支定界算法;Fan和Lu[6]研究了目标为最小化总发送时间与总发送费用之和的问题,其中每个可用时间段内完工工件在可用时间段结束时刻发送,证明了问题是强NP-难的,并提出了2-近似算法与分支定界算法。对于机器可用时间段长度不大于给定常数、且不可用时间段也需要安排的情况,Qi等[7]对于目标为最小化总完工时间的问题进行了研究,证明问题是强NP-难的,并给出3个近似算法与分支定界算法;Akturk等[8-9]从实际生产情况出发也研究了该问题,将变更加工工具所需时间视为不可用时间,并且在文献[9]中证明基于工件按加工时间的非降序(SPT序)安排加工所得的算法性能比为2;Qi[10]将这个性能比进行了改进。据查,目前尚未见研究不可用时间段需要安排,且同时考虑工件的加工与发送的供应链排序问题的相关报道。

本文安排如下:第1节对所研究问题进行具体介绍;第2节针对工件加工允许中断的情况,借助其最优序的性质,得到问题的最优算法;第3节针对工件加工不允许中断的情况,证明问题是强NP-难的,进一步提出近似算法,并通过分析得到算法的近似比为2。

1　问题的描述

给定一台机器及一个含n个工件的工件集J = {J1,J2,···,Jn}。这台机器1次最多只能加工1个工件,而且仅在可用时间段内加工工件,在不可用时间段内不可加工工件。机器的每个可用时间段长度不超过T,每个不可用时间段的长度为t。工件Jj的加工时间为pj(j = 1,2,···,n),且在零时刻即可开始加工。由于机器存在不可用时间段,工件的加工有两种情形:允许中断与不允许中断。工件的加工允许中断是指,若工件的加工被机器当前的不可用时间段中断,则在机器的下一个可用时间段内加工可继续进行;工件的加工不允许中断是指,若工件在机器当前的可用时间段内无法完全加工,则在机器的下一个可用时间段内加工。多个已完工工件可组成一批由一个无容量限制的运输工具发送给客户。第j批工件的发送时间为第j个可用时间段的结束时间,记为Dj。每次发送的费用为α,总发送费用记为CT。如何安排工件的加工、发送,以及不可用时间段,使总发送时间与总发送费用之和最小化,是问题的目标。因此,研究的问题有两个,采用三参数法可将两个问题分别表示为:

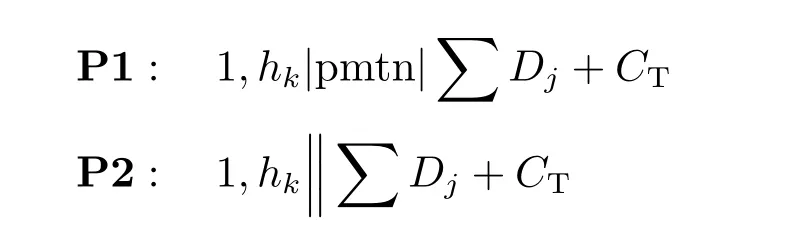
其中,hk表示加工机器有多个不可用时间段;pmtn表示工件的加工允许中断。

值得注意的是,如果工件的加工是不允许中断的,那么由于机器的可用时间长度至多为T,所以在问题P2中任意工件Jj(j = 1,2,···,n)的加工时间pj应满足pj≤T,否则,实例无可行序。

2　工件允许中断的情形

对于问题P1:1,hk|pmtn|ΣDj+ CT,即工件加工允许中断的情形,先分析最优序的性质,然后寻求问题的最优序。

2.1问题P1最优序的性质

(1)工件按加工时间的非降序(SPT序)进行加工;

(2)机器的每个不可用时间段的开始时间为kT +(k-1)t(k = 1,2,···),而且在所有工件完工之前,加工机器除不可用时间段之外无空闲;

(3)如果工件Ji在工件Jj之前完工,则工件Ji的发送时间不晚于工件Jj;

(4)运输工具的发送时间为kT+(k-1)t(k=1,2,···)。

利用文献[3,10]中的方法,易得引理1是正确的。

2.2问题P1的最优算法A1

算法A1执行步骤如下:

步骤1从0时刻开始,在机器上按照工件加工时间的非降序(SPT序)尽早地加工工件;

步骤2在kT +(k-1)t(k = 1,2,···)时刻将所有已完工工件组成一批发送给客户,并安排不可用时间段。

定理1算法A1可在多项式时间O(nlogn)内得到问题P1:1,hk|pmtn|ΣDj+ CT的最优序。

证明算法A1的步骤1满足引理1中的(1),即工件的加工阶段与最优序相同。步骤2中要求在时刻kT +(k-1)t(k = 1,2,···)安排完工工件的发送及不可用时间段,这满足了引理1中的(2)～(4),即完工工件的发送及不可用时间段的安排与最优序相同。因此,算法A1得到的排序即为最优序。

另外,算法A1中工件的排序需要时间O(nlogn),其余步骤需要时间O(n),因此,算法A1的时间复杂度为O(nlogn)。

3　工件不允许中断的情形

3.1问题P2的性质

首先,需要分析工件加工不允许中断时问题P2的困难性。于是,得到下面的定理。

定理2问题P2:1,hk‖ΣDj+CT是强NP-难的。

证明考虑问题P2:1,hk‖ΣDj+ CT的特殊情况:当机器可用时间段长度等于给定常数时,问题P2转化为文献[6]所研究的问题,而后者被证明是强NP-难的。因此,问题P2:1,hk‖ΣDj+ CT至少也是强NP-难的。

接下来,讨论问题P2最优序所具备的一些性质。

引理2若问题P2:1,hk‖ΣDj+ CT存在最优序,则最优序一定满足以下条件:

(1)工件按加工时间的非降序(SPT序)进行加工;

(2)在所有工件完工之前,加工机器除不可用时间段之外无空闲;

(3)若工件Ji在工件Jj之前完工,则工件Ji的发送时间不晚于工件Jj。

显然,由引理1可推出引理2的证明。

3.2问题P2的算法A2

定理3说明除非P = NP,否则不可能在多项式时间内找到问题P2的最优解。因此,提出一个近似算法来求解问题P2。

为方便起见,将工件按加工时间的非降序(SPT 序)重新编号,使得p1≤p2≤···≤pn。

算法A2执行步骤如下:

步骤1从0时刻开始,在机器上按照工件加工时间的非降序(SPT序)尽早地加工工件,在保证可用时间段尽量长以及工件加工不被中断的前提下,尽量晚地安排不可用时间段;

步骤2在每个可用时间段结束时间将所有已完工工件组成一批发送给客户。

下面,分析算法A2的性能比。

定理4对于问题P2:1,hk‖ΣDj+ CT,算法A2是2-近似算法。

证明用σ∗、δ∗及δ分别表示问题P1的最优序、问题P2的最优序及由算法A2得到的问题P2的排序。用F(σ∗)、F(δ∗)及F(δ)分别表示问题P1的最优值、问题P2的最优值及排序δ得到的目标函数值。

由于δ∗也是问题P1的可行序,于是

同时,根据问题P1的最优序σ∗,构造一个新的排序˜δ:如果在σ∗中工件Jj被某不可用时间段中断,那么在˜δ中,工件Jj被单独安排在一个可用时间段内加工,在其完工时间发送Jj并且增加一个不可用时间段;其余未中断工件尽早加工发送,且不可用时间段的安排不变。

显然,˜δ是问题P2的一个可行序。图1、图2与图3分别为工件Jj、Jj+1、Jj+2及Jj+3在问题P1的最优序σ∗、算法A2求解问题P2的所得序δ以及问题P2的可行序˜δ中加工情况的示例。

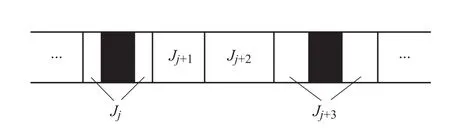
图1　在σ∗中Jj与Jj+3的加工被中断Fig.1 Jobs Jjand Jj+3are interrupted in σ∗

图2　在δ中Jj、Jj+1与Jj+2在同一个可用时间段内加工Fig.2 Jobs Jj,Jj+1and Jj+2are processed in the same available time interval in δ

图3　在?中Jj、Jj+3分别单独在一个可用时间段内加工Fig.3 Jobs Jjand Jj+3are processed in the respective available time interval in˜δ

由˜δ的构造过程可以看出,δ中每个工件的完工时间都不超过˜δ中相应工件的完工时间。于是,δ中每个工件的发送时间都不超过˜δ中相应工件的发送时间。又因为δ中的总发送次数比˜δ中的总发送次数少,所以

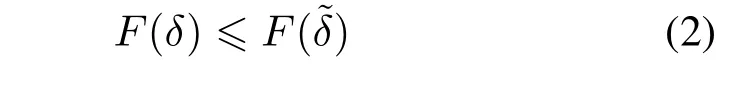
式中,F(˜δ)表示排序˜δ得到的目标函数值。

对于问题P1的最优序σ∗,用p[j]表示第j个位置工件的加工时间,用L表示总发送次数,用ni、Di分别表示第i个发送批Bi中工件的个数及发送时间。于是,问题P1的最优目标函数值为而排序˜δ对应的目标函数值F(˜δ)满足以下不等式:

又由于

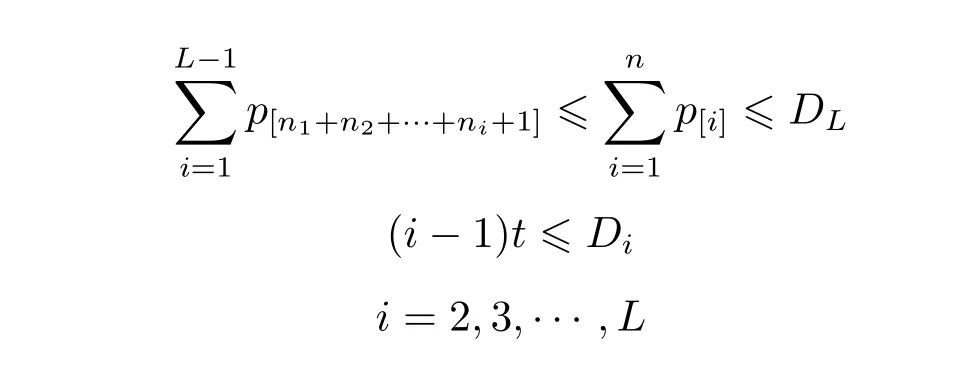
所以,不等式(3)可进一步化简为

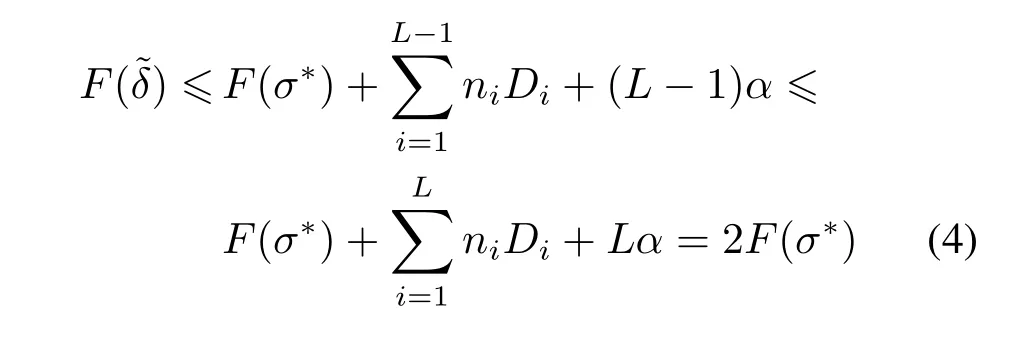
结合不等式(1)、(2)及(4),可以得到:

4　结语

在本文研究的单机供应链排序问题中,加工机器的每个可用时间段长度不超过T。所有工件需在机器的可用时间段内加工,完工后由运输工具在每个可用时间段结束时间发送给客户。如何安排工件的加工、发送,以及机器的各个不可用时间段,以使总发送时间与总发送费用之和最小是问题的目标。如果工件的加工允许中断,在分析其最优序性质的基础上,给出多项式时间最优算法。如果工件的加工不允许中断,证明问题是强NP-难的,并提出一个2-近似算法。

参考文献:

[1]陈荣军,唐国春.装配系统的供应链排序问题[J].数学的实践与认识,2011,41(18):50-56.

[2]POTTS C N.Analysis of a heuristic for one machine sequencing with release dates and delivery times[J].Operations Research,1980,28(6):1436-1441.

[3]HALL N G,POTTS C N.Supply chain scheduling:Batching and delivery[J].Operations Research,2003,51(4):566-584.

[4]CHEN Z L,VAIRAKTARAKIS G L.Integrated scheduling of production and distribution operations[J].Management Science,2005,51(4):614-628.

[5]CHEN W.Minimizing total flow time in the singlemachine scheduling problem with periodic maintenance[J].Journal of Operations Research Society,2006,63(4):567-567.

[6]FAN J,LU X W.Supply chain scheduling problem in the hospital with periodic working time on a single machine[J].Journal of Combinatorial Optimization,2015,30(4):892-905.

[7]QI X,CHEN T,TU F.Scheduling the maintenance on a single machine[J].Journal of Operations Research Society,1999,50(10):1071-1078.

[8]AKTURK M,GHOSH J,GUNES E.Scheduling with tool changes to minimize total completion time:a study of heuristics and their performance[J].Naval Research Logistics,2003,50(1):15-30.

[9]AKTURK M,GHOSH J,GUNES E.Scheduling with tool changes to minimize total completion time:basic results and SPT performance[J].European Journal of Operational Research,2004,157(3):784-790.

[10]QI X.A note on worst-case performance of heuristics for maintenance scheduling problems[J].Discrete Applied Mathematics,2007,155(3):416-422.

简讯

A Single-machine Supply Chain Scheduling Problem with Restricted Availability Intervals

FAN Jing
(School of Science,Shanghai Polytechnic University,Shanghai 201209,P.R.China)

Abstract:A single-machine supply chain scheduling problem with multiple restricted availability intervals was studied.The length of each availability interval was no more than a given constant and the length of each unavailability interval was fixed.Jobs were processed in availability intervals on the machine and the completed jobs were delivered in batches to a customer by one vehicle without capacity restriction.The departure time of each delivery batch was set to the end time of every availability interval and the cost of each delivery batch was fixed.The objective was to minimize the sum of total delivery time and total delivery cost by scheduling the production and delivery of every job as well as the unavailability intervals.If jobs were preemptive,the optimal schedule in the polynomial time O(nlogn)was obtained.If jobs were non-preemptive,it was proved that the problem is strongly NP-hard and a 2-approximation algorithm was presented.

Keywords:availability interval;supply chain scheduling;strongly NP-hard;approximation algorithm

基金项目:上海第二工业大学青年教师培养科研项目(No.201513)资助

通信作者:范静(1979–),女,山西长治人,副教授,硕士,主要研究方向为排序论。电子邮箱fanjing@sspu.edu.cn。

收稿日期:2015-07-01

文章编号:1001-4543(2016)01-0045-05

中图分类号:O223

文献标志码:A