散射中心的时频像特征研究
2016-04-20郭琨毅牛童瑶屈泉酉盛新庆北京理工大学信息与电子学院北京100081
郭琨毅 牛童瑶 屈泉酉 盛新庆(北京理工大学信息与电子学院 北京 100081)
散射中心的时频像特征研究
郭琨毅*牛童瑶屈泉酉盛新庆
(北京理工大学信息与电子学院 北京 100081)
摘要:散射中心是高频区电磁散射的重要特征,其属性特征,如散射幅度、位置,对方位的依赖性对于雷达成像及目标识别具有重要意义。与其它雷达图像相比,时频图像能更完整地反映出散射中心的属性特征,但目前关于不同散射中心的时频像特征研究还不完整。该文首先基于散射中心模型,从理论上分析了各个散射中心时频像的特征,然后通过全波法电磁计算得到了典型结构目标的散射数据,从数值上验证了对时频图像特征的理论分析,最后总结了不同散射中心的时频像特征,此结论有助于从时频像中直观地判断目标的散射中心类型和其对应的物理结构特点,可为基于时频像的雷达目标特征提取与识别提供一定的理论参考。
关键词:电磁散射;散射中心;属性;时频变换
1 引言
散射中心反映了目标特定结构和尺寸的精细物理及几何属性[1]。随着雷达分辨率的提高,目标上所有散射中心不能当作理想点源来看待,而应考虑其散射对频率和方位角的依赖关系。一般来说,对于不同的散射机理,散射中心的方位特性是不同的,这些方位特性反应了目标的几何结构特点。散射中心的方位依赖性是散射中心的重要属性特征,能够更加精确地构建SAR目标的散射特性,对雷达目标识别提供了重要信息[2,3]。随着雷达系统的发展和分辨率的提高,在大的成像孔径下,雷达目标散射中心的方位特性分析、建模及提取研究受到越来越多的关注[4]。
雷达1维距离像历程图可以反映出散射中心径向位置分布及其随方位角变化的依赖关系[5],然而1维距离像的径向分辨率受到带宽的限制。当距离分辨率较低时,曲面、曲棱边散射所形成的滑动型散射中心在1维距离像历程图中不能清晰显示,常误判为位置固定的散射中心。SAR图像可以直接反映目标的2维散射中心分布,但是对于位置随雷达视线方位变化、散射幅度随方位起伏较大的散射中心在雷达图像上不能很好地聚焦,例如平面或直棱边散射所形成的散射中心,以及曲面、曲棱边散射所形成的滑动型散射中心。
时频图像可以展示各个散射中心对于方位角变化的依赖关系[6],其图像分辨率与带宽无关,而是受算法本身影响,如窗宽度和交叉相抑制效果[7]。多普勒频率虽然易受噪声干扰,但信号噪声所导致的时频像噪声,可以通过常用的去噪方法去除,如小波滤波等[8]。因此,时频像成为展示、分析、研究散射中心属性特征的重要方法。从图像上读取信息量角度或所能展示的散射中心类型的全备性角度来说,利用时频图像对目标进行识别能获得目标更多的物理和几何结构信息。
目前,常见的散射中心有镜面型散射中心、边缘(棱线)型散射中心、尖顶型散射中心、凹型体的多次反射型散射中心、行波蠕动波型散射中心和天线型散射中心等[9]。上述对散射中心分类多从其形成机理和属性特征出发,其对应的时频像特征辨识目前还没有较为全面的研究。经研究发现,有些散射中心的散射机理相同,但在时频图中表现为不同特征,而不同的散射机理,又可能有相同的时频图特征。为了便于散射中心在目标识别中的应用,本文研究了各种散射中心在时频图像中的特征,研究结论对目标识别、雷达图像理解具有一定的参考价值。
2 散射中心模型
目前已有代表性的散射中心模型包括:属性散射中心模型、滑动散射中心模型和爬行波散射中心模型。结合此3个模型,扩展目标的散射中心基本可以完备描述。
2.1 属性散射中心模型
目前最为完整的散射中心模型为属性散射中心模型[10],见式(1)。该模型是从几何绕射理论(GTD)和物理光学(PO)理论提出的,是较早的衰减指数模型、基于GTD散射中心模型的扩展。属性散射中心模型包含了散射中心的物理属性和几何属性,例如散射中心的后向散射场与频率和方位的关系,并且用一组描述位置、幅度、形状和方向的参数来说明每个散射中心的特征。属性散射中心模型其在GTD散射中心模型[11]的基础上增加了散射中心幅度对雷达观测方位关系的描述,包括两类不同的方位依赖性:局部型和分布型。
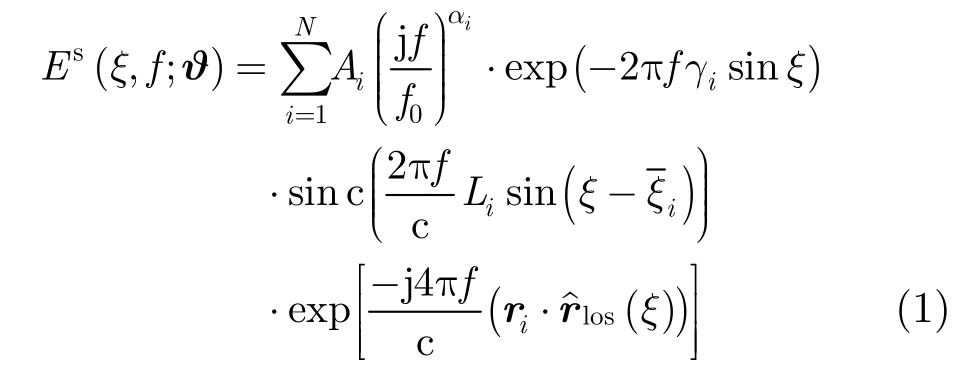
其中,Es表示目标上N个散射中心的后向回波之和,f为入射电磁波频率,f0为雷达中心频率,c为光速,ξ表示目标坐标原点相对于雷达的方位角,由欧拉角决定,为雷达观测方向单位矢量。每个散射中心由参数矢量表示。Ai为散射中心复振幅,αi代表了几种不同类型的散射中心,其取值为1/2的整数倍,表征了散射强度对频率的依赖性,ri为第i个散射中心的位置矢量,表征了散射中心对方位角的依赖关系,其中Li和分别表征了散射中心长度和(法线)相对于雷达视线的倾角。
分布型散射中心包括平板反射,柱面反射,二面体反射等,仅在特定的角度下可见,其幅度的方位依赖性满足式(2):
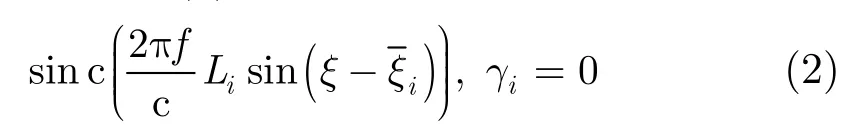
局部型散射中心包括三面体反射,角绕射,边缘绕射等,其在目标上的位置相对稳定,且在较大视角范围内可见,它们的散射幅度相对于方位角变化较缓慢,模型中采用一个衰减的指数函数对其近似描述:
2.1.1 色谱条件色谱柱:Acquity UPLC BEH C18(100 mm×2.1 mm,1.8 μm);流动相:0.1%甲酸溶液(A)-乙腈(B),梯度洗脱(0~1 min,5%B→25%B;1~3.5 min,25%B→40%B;3.5~4.5 min,40%B→50%B);流速:0.5 mL/min;柱温:40 ℃;进样量:1.0 μL。

经实际检验发现属性散射中心模型有其局限性,在大观测角范围内,局部性散射中心幅度随方位变化不能较好地描述,以及无法描述位置变化的滑动型散射中心。
2.2 滑动型散射中心模型
针对属性散射中心模型的不足,有人提出了多项式描述幅度起伏的模型,以及针对滑动型散射中心的模型[12],很好地描述了滑动散射中心的复杂特性,见式(4)
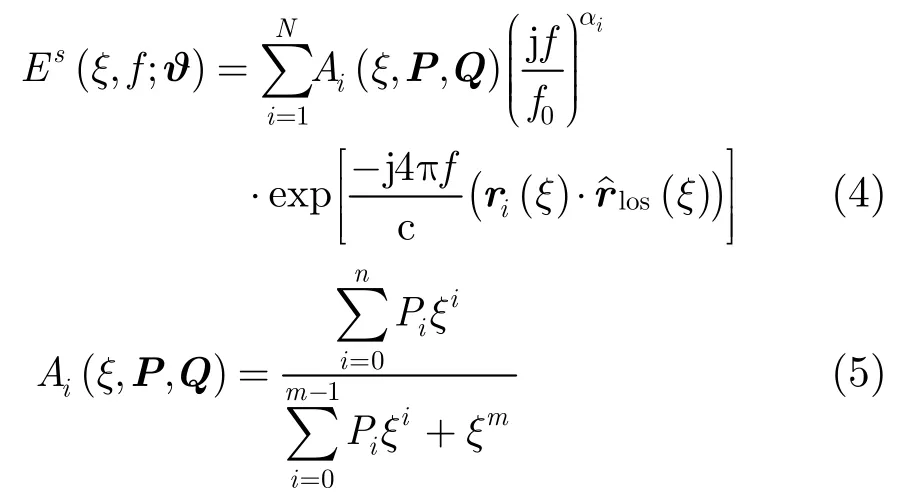
2.3 爬行波散射中心模型
以上的散射中心模型主要针对于单站情况,而针对双站雷达,一般采用单、双基地等效原理,将单站散射中心模型直接推广到双站情况。在单站雷达系统,有些弱散射中心,如爬行波和行波散射中心,对于散射场的贡献很小,一般可以忽略不计,因此模型中一般没有考虑。然而随着研究的深入发现,在双站雷达系统中,爬行波和行波形成的散射中心,其散射幅度在某些观测场景下(尤其是双站角大于等于90°时)贡献较强,不能忽略,必须要在模型中加以补充。因此有人提出了描述此类散射中心的爬行波散射中心模型[14,15]。
当平面电磁波入射到单曲面上时,如圆锥侧壁,电磁波在其表面爬行并沿绕射线切线方向不断辐射能量,出射点在一条母线上的绕射线方向平行,且在固定的双基地角下,雷达接收到的爬行波的传播距离相同,故其所形成的散射中心可等效为分布型散射中心,等效的单站散射中心模型为
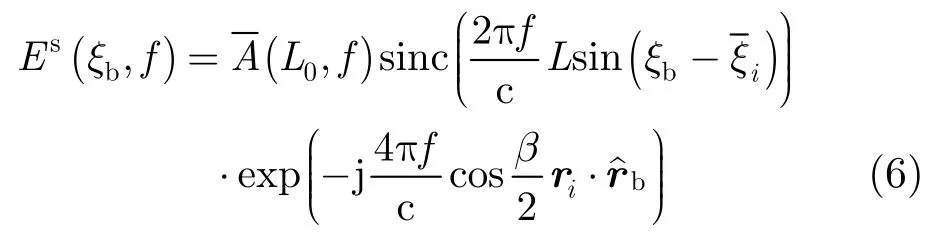
当平面电磁波入射到高次曲面,如椭球面上时,爬行波的绕射线不再平行,只有指向雷达接收方向的电磁波可以被观测和接收,且不同的观测角下接收到的爬行波的传播距离不同,因此等效的散射中心位置随着观测角的改变而在曲面上滑动,故此时爬行波形成的散射中心为滑动型散射中心。其散射中心模型为

3 散射中心不同属性特征与时频特征的对应关系
时频变换主要用于分析非平稳信号,描述信号频谱含量随时间的变化情况。时频变换方法有线性和非线性两种。典型的线性时频表示有短时傅里叶变换(STFT),Gabor展开和小波变换[17]。常见的非线性(双线性)时频表示法有WVD和Cohen类[18]。STFT算法简单,便于对图像特征的理解,因此下文理论分析采用此算法。STFT的缺点为不能兼顾频率与时间分辨率的要求,WVD解决了STFT的这一局限性,但引入了多个多普勒成分之间的交叉项的问题。Cohen类变换可以通过设计核函数来抑制传统WVD变换的交叉项,同时兼顾时间和频率分辨率。改进的时频变换算法均严格保证了原始信号的时频特征的不变性,重点在改进图像的质量,更清晰地展示信号能量、多普勒频率随时间的变化规律。因此本文对于散射中心时频特征的规律研究,不局限于STFT的结果,具有一般性。依据STFT的原理,时频像的输出结果可表示为

3.1 分布型散射中心的时频特征
对于分布型散射中心,其位置固定于目标上,其幅度的方位依赖性函数见式(2)。此函数仅在特定角度下幅度出现峰值,其余的角度下幅值较小。从STFT的原理可知,仅在时,时频像的幅度较大,而且在频率轴上宽度展宽呈现出幅值略有起伏的条带竖线,条带的宽度为窗函数的宽度,长度约为,而在其余的角度下时频像幅度近似为零。分布散射中心的时频像如图1(a)所示,纵轴为多普勒频率,用fD表示,图1(b)为对应散射中心的幅度依赖函数。时频像采用时频工具箱[19]的STFT方法实现。

图1 分布型散射中心的理论时频图
分布型散射中心的时频图竖线在频率轴上的宽度与此散射中心的尺寸成正比,所以当此散射中心的尺寸很小时,其时频像在频率轴上的分布不超过一个多普勒分辨单元,因此在时频图中呈现点状的分布。
凹腔体散射中心,例如三面角,在属性散射中心模型中将其归为局部型散射中心,但由于它可以视为由多个方向上连续出现的分布型散射中心的组合,其幅度在很大的观测角度下都很强,因此它具有局部型和分布型两类散射中心的特征,称为联合型散射中心,记为JSC,且其时频图像在频率轴上跨越多个频率分辨单元,所以在时频图像中呈现块状的高亮分布。
3.2 局部型散射中心的时频特征
对于局部型散射中心,其位置固定于目标上,在大观测角度范围内都有较强的散射幅度,其随方位角的起伏变化可采用有理多项式描述。从STFT的原理可知,在此大观测角度范围内,时频像的幅度较大。如果只针对一个散射中心的回波信号进行时频变换且此散射中心为局部型散射中心,则当频率分辨率足够高时,在每个角度下只对应一个多普勒频率值,所以在时频像中某一角度下的幅度近似为散射回波在这一角度下的幅值,由于散射回波的频率只与其相位有关,因此回波信号的幅值大小并不影响时频图中多普勒频率曲线的形状,如图2(a),图2(b)所示,其中图2(c),图2(d)分别为用一阶和二阶多项式描述的散射中心的幅度依赖函数。由式(6)可知时频像幅度随观测角度变化起伏较小。由于散射中心的位置不随角度变化,所以多普勒频率曲线是随散射中心位置矢量和雷达视线夹角(记为υ=变化的正弦(或余弦)曲线。为了检测或识别此类散射中心,可以对其进行投影变换得到1维-高维散射映射(One-Two/Three Dimensional Scattering Mapping,OTSM[20])图,局部型散射中心在OTSM图中呈现标准的圆周分布,如图2(e),图2(f)所示,其中x和y分别为散射中心所在平面的横、纵坐标。
3.3 滑动型散射中心的时频特征
对于滑动型散射中心,随着观测方位角的改变其位置在目标上滑动。此类散射中心的幅度随方位的起伏变化可用式(5)描述,图3(c),图3(d)为不同的散射中心幅度依赖函数,分别随着υ的增加而非线性增大和减小,记为g1和g2。与上述局部型散射中心相同,此散射中心回波信号的幅值决定了其时频像幅度的大小,并不影响时频像中多普勒曲线的形状,如图3(a),图3(b)所示。在大多数情况下,由于散射中心的位置随观测角度不断变化,见式(4),所以多普勒频率曲线是分布在时频图中的一条随υ变化的复杂曲线,可作为滑动散射中心的重要识别特征。滑动散射中心的多普勒曲线不再是简单的正弦或余弦曲线,因此在OTSM图中不是标准的圆周分布,如图3(e),图3(f),由此可以直观地将滑动散射中心与局部性散射中心分辨开来。
从分布型、局部型和滑动型散射中心的时频图可以看出,它们在时频图像中表现为不同的分布特点。图1和图3虽然都是由反射形成的散射中心,但其时频图像特征明显不同,可见相同的散射机理可能有不同的时频图像特征。同样,不同的散射机理可能会有相同的时频图像特征,例如单曲面圆锥爬行波形成的散射中心和平板这两个散射中心分别由绕射和反射形成,虽然散射机理不同,但其在时频图像中都表现为一条多普勒频率分布较宽、时间分布很窄的竖直亮线,如图1所示。

图2 局部型散射中心的理论时频图

图3 滑动型散射中心的理论时频图
4 典型目标的时频像特征
下文给出了球、圆锥、半椭球、圆柱、角反射器、圆台(上表面与侧面通过圆角过渡)6个简单目标在VV极化下的单站回波的时频图像特征。目标电磁散射数据通过已得到可靠性验证的精确全波数值法(FE-BI-MLFMA[21])计算获得。各目标的具体几何参数见表1,图4为各目标的散射中心位置分布图。各目标上散射中心的具体类型见表2。表中SC表示散射中心,SSC、LSC和DSC分别代表滑动型散射中心、局部型散射中心和分布型散射中心。

表1 目标尺寸

表2 散射中心的时频图分析
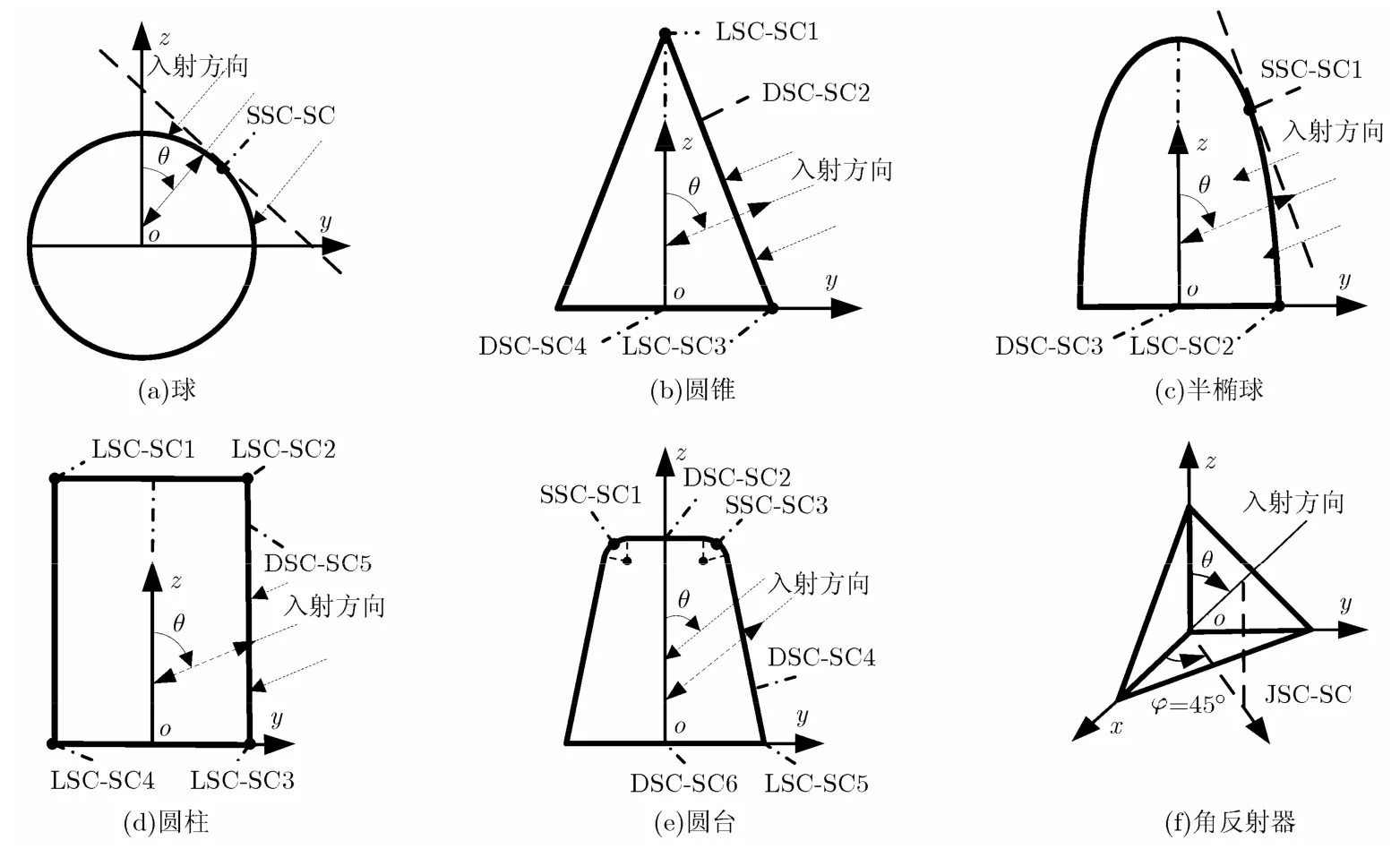
图4 目标散射中心分布
目标1球只有球面的镜面反射形成的散射中心,目标2圆锥主要有4种散射中心,分别为尖顶绕射、圆锥单曲面反射、圆锥底面棱边绕射和锥底平面的镜面反射,目标3半椭球相比于目标2增加了双曲面的反射这一情况形成的散射中心,目标4圆柱的散射中心主要有镜面反射和上下底面的棱边绕射,目标5圆台的散射中心分布如图4(e)所示,目标6为角反射器,这类散射中心常见于飞机的座舱、进气道、尾喷管等处,会产生的很强的散射,是目标识别的主要散射源。各目标的单站时频像(Mono-TFR),以及包含的各类散射中心特征,如图5所示。雷达视线变化:,对于目标6,,其他目标φ=90°。
球的散射中心为球心,散射机理为球面的镜面反射。当θ变化时,因为散射中心位置不变且在坐标原点,所以多普勒频移始终为零,为图中5(a)所示的一条横线。圆锥的锥顶为尖顶散射,此类散射中心在大角度下都可观察得到且幅度起伏较小,如图5(b)SC1所示。由图5(c)SC1可知,当雷达视线改变时,散射中心的位置也会在半椭球体的侧壁滑动,强度会随着侧壁曲率半径的增加而增大。圆锥、圆台和圆柱侧壁为镜面反射,只在一个小的角度下出现大强度的散射,表现为时频图像中的一条竖直亮线,如图5(b),5(d),5(e)所示。在圆锥底面棱边和圆柱上下表面棱边会产生棱边绕射,在时频图中表现为起伏较小的连续的正弦曲线。由图5(f)可知,角反射器在时频图中表现为块状区域,其散射机理为腔体内的多次反射。上述实际目标回波的时频特征规律,与理论分析结果一致。

图5 目标散射中心的单站时频图像
通过观察以上简单目标的时频图像,可以得到镜面反射型、边缘绕射型、尖顶绕射型、多次反射型等各个散射中心在时频图像当中的特征。根据散射中心在时频图中的特征可分为连续性和非连续性特征两大类。连续性特征是指随着雷达视线的移动在较大角度范围内都能观察到的散射中心,如锥体的尖角等形成的散射中心位置不随雷达视线变化的固定型散射中心,和半椭球侧壁等曲面形成的散射中心位置随雷达视线移动的滑动型散射中心。非连续性散射中心是指在时频图像中表现为块状、点状、和竖条状等区域的散射中心,包括随着雷达视线的移动只在很小的角度范围内出现,其余角度下观察不到,具有快闪特性的散射中心,例如平板散射中心在时频图中表现为一条近似竖线的分布。也包括在时频图中表现为散射强度大的块状区域的散射中心,例如三角反射器等凹腔体结构。各类散射中心时频图特征与目标几何结构特点的对应关系,总结归纳如表3所述。可见,基于时频图像特征,能够方便人们直接读取目标散射中心的物理及几何结构信息,对雷达目标识别有很好的应用价值。

表3 时频像特征与目标几何结构特点的对应关系
5 结束语
雷达目标时频图像对于目标识别有着重要意义,散射中心在雷达图像中呈现出点、块、条、不规则区域等高亮分布。由于散射中心和目标的几何结构密切相关,因此可以通过时频图像提取目标的散射中心分布,进而获取目标的物理尺寸等信息。基于时频图像特征可知,散射中心有连续型和非连续型两大类。连续型散射中心对应的目标结构为尖顶或光滑曲面,非连续型散射中心对应的目标结构可能为平板或凹腔体等。对于不同的散射机理如反射和爬行波绕射,在时频图像中可能会表现为类似的分布特征,而对于相同的散射机理如平板反射和半椭球体的侧表面反射,在时频图像中表现为不同的分布特点。因此对散射中心的图像特征的研究,不仅丰富了对散射中心属性特征的认识,而且可以利用散射中心的时频像特征,方便地解读目标的几何结构信息,这对目标特征提取以及目标识别具有理论和应用价值。
参考文献
[1]刘拥军,葛德彪,张忠治,等.有属性的散射中心理论及应用[J].电波科学学报,2004,18(5):559-563.LIU Yongjun,GE Debiao,ZHANG Zhongzhi,et al.The theory of attributed scattering centers[J].Chinese Journal of Radio Science,2003,18(5):559-563.
[2]张亚军.基于属性散射中心模型的SAR目标自动识别[D].[硕士论文],西安电子科技大学,2014.ZHANG Yajun.Automatic recognition of SAR targets based on attribute scattering center model[D].[Master dissertation],Xidian University,2014.
[3]付耀文,贾宇平,庄钊文.基于一维散射中心匹配的雷达目标识别[J].电子学报,2006,34(3):404-407.FU Yaowen,JIA Yuping,and ZHUANG Zhaowen.Radar target classification based on one dimensional scattering centers matching[J].Acta Electronica Sinica,2006,34(3):404-407.
[4]张肖,周建江,汪飞.基于空域滤波的雷达目标二维散射中心快速提取[J].电子与信息学报,2014,36(3):523-528.doi:10.3724/SP.J.1146.2013.00365.ZHANG Xiao,ZHOU Jianjiang,and WANG Fei.Fast extraction of radar target 2D scattering centers based on spatial filtering[J].Journal of Electronics & Information Technology,2014,36(3):523-528.doi:10.3724/SP.J.1146.2013.00365.
[5]杨莉.一维距离像特性分析及目标识别方法研究[D].[硕士论文],哈尔滨工业大学,2014.YANG Li.Study of feature analysis and target recognition for high resolution range profile[D].[Master dissertation],Harbin Institute of Technology,2014.
[6]贺思三.雷达成像中的非理想散射现象分析[D].[硕士论文],国防科学技术大学,2005.HE Sisan.The analysis of nonideal scattering phenomena in radar imaging[D].[Master dissertation],National University of Defense Technology,2005.
[7]CHEN V C.Time-frequency Transforms for Radar Imaging and Signal Analysis[M].Boston:Artech House,2001:23-42.
[8]周洋.基于小波变换的非局部图像去噪方法研究[D].[硕士论文],西安电子科技大学,2014.ZHOU Yang.Non-local image denoising method based onwavelet transform[D].[Master dissertation],Xidian University,2014.
[9]黄培康,殷红成,许小剑,等.雷达目标特性[M].北京:电子工业出版社,2005:2-7.HUANG Peikang,YIN Hongcheng,XU Xiaojian,et al.Radar Target Features[M].Beijing:Publishing House of Electronics Industry,2005:2-7.
[10]POTTER L C and MOSES R L.Attributed scattering centers for SAR ATR[J].IEEE Transactions on Image Processing,1997,5(1):79-91.
[11]POTTER L C,CHING D M,CARRIERE R,et al.A GTD-based parametric model for radar scattering[J].IEEE Transactions on Antennas and Propagation,1995,43(10):1058-1067.
[12]GUO Kunyi,LI Qifeng,SHENG Xinqing,et al.Sliding scattering center model for extended streamlined targets[J].Progress In Electromagnetics Research,2013,139(3):499-516.
[13]GUO Kunyi and SHENG Xinqing.A precise recognition approach of ballistic missile warhead and decoy[J].Journal of Electromagnetic Waves and Applications,2009,23(14):1867-1875.
[14]QU Quanyou,GUO Kunyi,and SHENG Xinqing.An accurate bistatic scattering center model for extended coneshaped targets[J].IEEE Transactions on Antennas and Propagation,2014,62(10):5209-5218.
[15]QU Quanyou,GUO Kunyi,and SHENG Xinqing.Scattering centers induced by creeping waves on streamlined coneshaped targets in bistatic mode[J].IEEE Antennas and Wireless Propagation Letters,2015,14:462-465.
[16]PATHAK P H,BURNSIDE W D,and MARHEFKA R J.A uniform GTD analysis of the diffraction of electromagnetic waves by a smooth convex surface[J].IEEE Transactions on Antennas and Propagation,1980,28(5):631-642.
[17]CARBOR D.Theory of communication[J].Journal of the Institute of Electrical Engineers,1946,93:429-457.
[18]刘海燕,田钢,石战结.几种时频分析方法的比较和实际应用[J].CT理论与应用,2015,24(2):199-208.LIU Haiyan,TIAN Gang,and SHI Zhanjie.The comparison of time-frequency analysis methods and their applications[J].Computerized Tomography Theory and Applications,2015,24(2):199-208.
[19]FLANDRIN P.Time-Frequency Toolbox[OL].http://tftb.nongnu.org/.Jul.2011
[20]周剑雄.光学区雷达目标三维散射中心重构理论与技术[D].[博士论文],国防科学技术大学,2006.ZHOU Jianxiong.The theory and methodology of reconstructing 3D position of scattering centers in the optical region[D].[Ph.D.dissertation],National University of Defense Technology,2006.
[21]SHENG X Q,JIN J M,SONG J M,et al.On the formulation of the hybrid finite-element boundary-integral methods for 3D scattering using multi-level fast multipole algorithm[C].IEEE Antennas and Propagation Society International Symposium,Atlanta,GA,USA,1998,Vol.1:236-239.
郭琨毅:女,1976年生,副研究员,博士,主要研究方向为目标散射特性、目标成像、目标识别技术等.
牛童瑶:女,1991年生,硕士生,研究方向为目标散射特性.
屈泉酉:男,1988年生,博士生,研究方向为复杂目标电磁特性及其应用.
盛新庆:男,1968年生,教授,博士生导师,主要研究方向为计算电磁学、目标电磁特性、微波成像及遥感、天线理论及设计等.
of China(61471041)
Research on Signatures of Scattering Centers Shown in Time-frequency Representation
GUO KunyiNIU TongyaoQU QuanyouSHENG Xinqing
(School of Information and Electronics,Beijing Institute of Technology,Beijing 100081,China)
Abstract:Scattering centers are important features of electromagnetic scattering at high frequencies.The aspect dependency of the amplitude and location of a scattering center has a significant influence on radar imaging and target recognition.Compared with other radar images,the Time-Frequency Representation(TFR)of radar returns more clearly presents features of scattering centers.In this paper,the signatures of TFR of different types of scattering centers are investigated theoretically and numerically.In numerical experiments,the scattering responses of several typical targets are computed by the full-wave numerical method.The conclusion of this paper on signatures of TFR of scattering centers can provide a theoretical reference for the feature extraction and target recognition from TFRs.
Key words:Electromagnetic scattering; Scattering centers; Attributes; Time-frequency transform
基金项目:国家自然科学基金面上项目(61471041)
*通信作者:郭琨毅guokunyi@bit.edu.cn
收稿日期:2015-05-18;改回日期:2015-11-09;网络出版:2016-01-04
DOI:10.11999/JEIT150598
中图分类号:TN011
文献标识码:A
文章编号:1009-5896(2016)02-0478-08
Foundation Item:The National Natural Science Foundation
