伪码-线性调频复合信号参数估计理论性能分析
2016-04-20电子科技大学电子工程学院成都611731
王 佩 祝 俊 唐 斌(电子科技大学电子工程学院 成都 611731)
伪码-线性调频复合信号参数估计理论性能分析
王佩*祝俊唐斌
(电子科技大学电子工程学院成都611731)
摘要:针对伪码-线性调频复合信号参数估计的理论性能评价问题,该文分析了分步估计方法对参数估计的影响,给出了较高信噪比时分步估计方法的理论近似性能;推导了高斯白噪声环境中伪码-线性调频信号参数无偏估计的修正克拉美-罗下限(MCRLB)的解析表达式。利用伪码序列的统计特征推导出起始频率、调制斜率、初始相位及码元宽度参数联合估计的修正Fisher信息矩阵,从而得到各参数估计的MCRLB。对结果进行了对比分析,并通过数值仿真实验,证明了该理论下限的有效性。
关键词:参数估计;伪码-线性调频复合信号;分步估计法;修正克拉美-罗限
1 引言
伪码-线性调频(PRBC-LFM)复合信号兼具伪码信号和线性调频信号两种信号的优点[1],在雷达、通信及引信等领域中均有应用[2-5]。研究非合作环境中PRBC-LFM复合信号的参数估计问题对电子侦察具有重要意义。
对PRBC-LFM复合信号的参数估计研究已有部分文献提及[6-9]。该类复合信号参数估计常用一种分步估计方法:首先平方消除伪码信息,进而估计线性调频参数,然后解线性调频得到相位编码信号估计码速率。不同算法之间的区别在于选取的常规信号参数估计算法不同[7-9]。然而在性能分析方面,现有文献仅从仿真实验的角度给出算法均方根误差的大小以证明其算法的有效性,并未给出分步估计算法的理论性能,也未给出一种类似于克拉美-罗下限(CRLB)的理论评价工具。当信号中存在数字调制如二相编码调制成分的时候,信号参数估计的CRLB难以解析推导,目前文献中多使用均方根误差来说明其性能[10,11]。
由于数字调制存在时,信号参数估计的CRLB难以解析推导。文献[12]通过简化CRLB推导过程中的一个条件概率密度计算,提出了单个参数估计的修正克拉美-罗下限(MCRLB)的概念,并将其用于合作通信中部分参数的估计;文献[13]在此基础上将MCRLB扩展为多个信号参数的联合估计问题,通过Fisher信息矩阵的推导得到了各参数联合估计的下限;文献[14]给出了相位编码信号在升余弦脉冲和矩形脉冲两种情况下码元宽度估计的MCRLB;文献[15]讨论了未知数字调制的连续相位调制信号参数估计的MCRLB,并对比了参数的单独估计与联合估计的区别;文献[16]推导了基于全球移动通信系统的多基地被动雷达探测目标的参数误差的MCRLB;文献[17]将MCRLB用于PRBC-LFM复合调制雷达信号的参数估计,得到了各参数单独估计时的MCRLB,但未考虑多调制参数的联合估计问题。
本文针对高斯白噪声环境中PRBC-LFM复合信号多参数联合估计问题,首先分析了分步估计对信号参数估计的影响,然后通过合理假设推导了各参数估计的修正Fisher信息矩阵,从而得到参数联合估计的MCRLB,并通过数值仿真与已有参数估计算法性能进行对比,验证了理论下限的有效性。
2 PRBC-LFM分步估计方法性能
针对PRBC-LFM复合信号,文献[7~9]选取的参数估计方法均基于一种分步估计方法。其框图如图1所示。

图1 分步估计算法流程
从估计流程中可以看出,此类方法对起始频率、调制斜率的估计受平方运算的影响,对码速率的估计受到解线性调频误差的影响。
2.1 平方运算对参数估计的影响
设具有N点观测样本的离散数字信号模型为

其中,{w(n)}为方差σ2的独立同分布复高斯白噪声随机变量;为待估计信号,A为信号幅度,φ(n)为n时刻的信号相位。信噪比为。对信号进行平方运算,得到
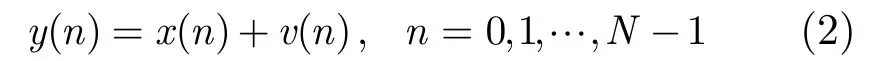
平方后的噪声序列包含两部分,分别设为v1(n)和v2(n),则有

根据w(n)的性质可知:


其中v1(n)服从高斯分布;v2(n)实部为两个相互独立的高斯随机变量的平方差构成的新随机变量,虚部为这两个独立随机变量的积,其总的概率密度分布较为复杂;v(n)为两种不同分布噪声序列的和。此时信号的信噪比为

由式(7)可以看出,相比于平方前的信噪比,平方后的信噪比至少有4倍也即6 dB的降低,该结论也可通过频域方法得出[18]。
由文献[7~9]的结论可知,分步估计算法通常在信噪比优于2 dB时估计误差才可能收敛。此时,平方后的噪声序列中v1(n)为主要成分,其占据噪声总功率的比例为

根据式(8)可知,当信噪比较高时,高斯分布的噪声占据噪声的主要成分。因此,在较高信噪比时,复合信号分步估计法对调频参数的估计性能可以近似为高斯噪声中的线性调频参数估计。此时参数的估计下界分别为[19]
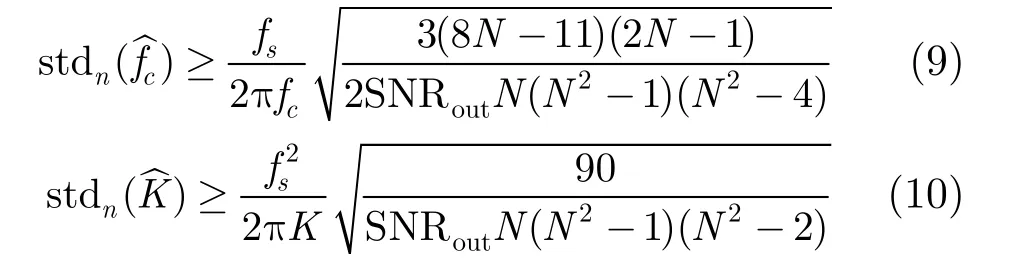
2.2 解线性调频对参数估计的影响
解线性调频运算的目的是将信号中的线性调频成分通过重构消除掉,以方便后续处理。此过程并不改变编码信号的调制参数,且噪声解线性调频后依然是均值为0、方差为σ2的高斯白噪声,因此从理论上讲也不会对相位编码信号的参数估计性能产生影响。
综上,PRBC-LFM复合信号的分步估计对参数估计的影响主要由平方运算产生。平方导致了至少6 dB的信噪比损失;在较高信噪比时,平方后的噪声序列可以假设为均值为0的高斯随机序列。
3 PRBC-LFM信号估计的MCRLB
3.1 信号模型与基本假设
设I(u)为CRLB对应的Fisher信息矩阵,则

由文献[13]可知,如果干扰向量v中存在未知数字调制或者非高斯噪声成分,则其概率密度函数

通常难以解析计算,从而I(u)难以解析计算。此时经典的CRLB虽然存在,却难以解析给出。

从而给出了修正克拉美-罗下限:
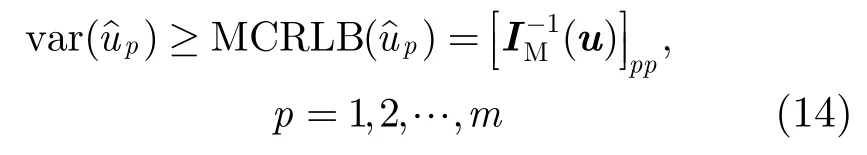
由于计算时对概率密度分布的简化,导致了MCRLB通常要比CRLB松弛。也即

但文献[13]指出,很多实际情况下,MCRLB与CRLB是非常接近的,当干扰向量v为确定已知参数且观测时间充分长时,二者相等。因此在CRLB难以给出的情况下,利用MCRLB对算法的估计性能进行评价具有重要意义。
针对式(1)的离散模型,设其中复合信号模型为

式中幅度A为常数,则码元宽度近似采样点数D、初始相位θ0、起始频率f0、和调制斜率α等调制参数构成待估计参数向量;未知随机离散调制序列及噪声功率σ2构成干扰参数向量; g(n)为伪码信号一个子脉冲的矩形包络。
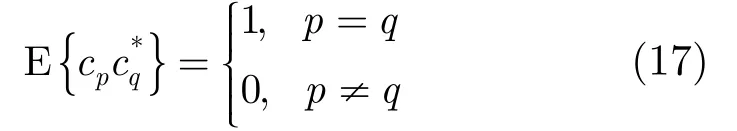
3.2 修正的Fisher信息矩阵计算
根据信号模型,可知条件概率密度函数

因此,修正的Fisher信息矩阵IM(u)的元素为

3.2.1对角元素计算考虑p=q时,有

则通过计算和化简可以得到
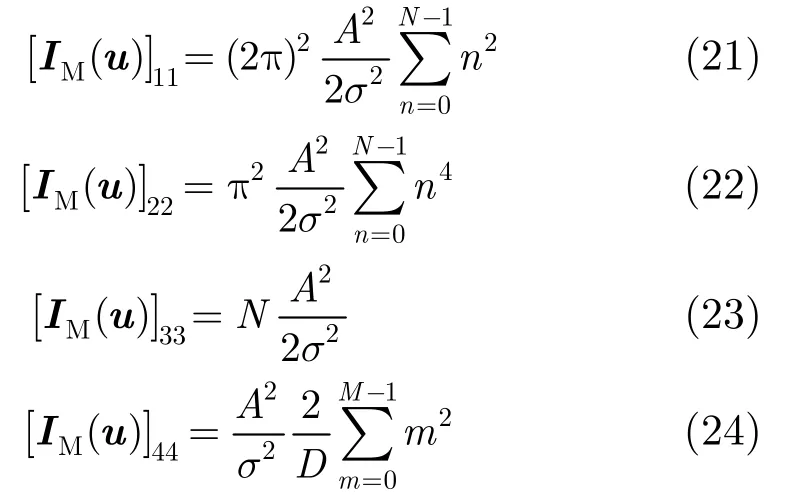

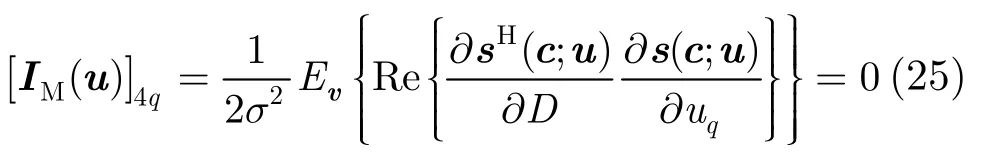
同理,当q =4,1,2,3
p =时,有

这表明,在基本假设成立情况下,码元宽度的估计与起始频率、调制斜率以及相位无关。
当p≠4且q≠4时,分别可以得到
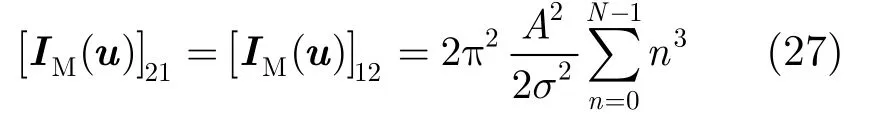
第1行第3列和第3行第1列元素为
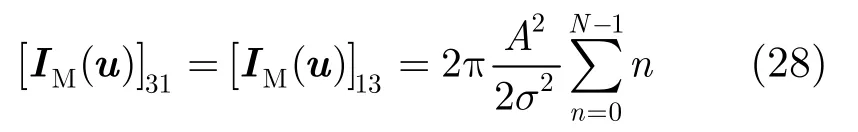
第2行第3列和第3行第2列元素为
综上,参数联合估计的修正Fisher信息矩阵为

式中的3阶方阵Iup为

对矩阵求逆可以得到
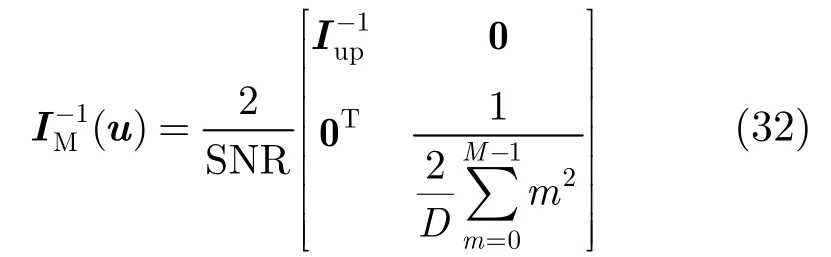
则各参数联合估计的MCRLB结果为

选用归一化均方根误差(NRMSE)表征算法性能,对各参数的MCRLB进行归一化分析。由于要与文献[7]估计性能进行对比,故只考虑起始频率、调制斜率和码元宽度等参数。
设样本数据的真实起始频率为fc,调制斜率为K,码元宽度为Td,采样频率为fs,则有,,则真实值估计的下限为
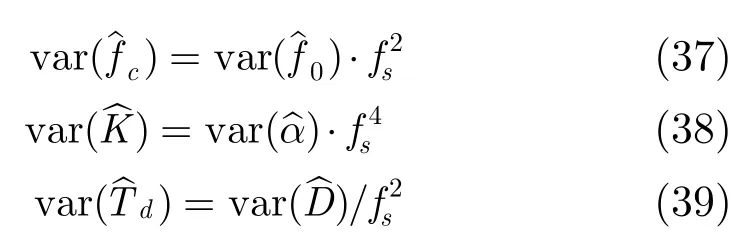
记均方根误差意义下的归一化标准差为std,则有
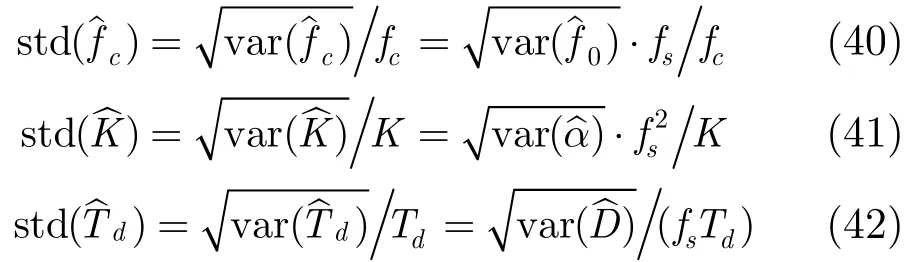
4 数值仿真与分析
选取具有代表性的文献[7]中的估计方法进行仿真,并与本文分析得到的分步估计得到的起始频率、调制斜率的理论性能以及MCRLB的理论结果进行对比。
实验采取与文献[7]仿真实验类似的参数设置,但为了体现伪码特性,每次Monte Carlo试验中将随机产生一组伪码序列。具体参数为:线性调频初始频率为16 MHz,信号脉宽10 μs,调制斜率1012Hz/s;伪码速率为2 MHz,每次产生20个码元长度的数据;信号采样率为100 MHz,FFT点数为1024,滑动求和点数为20;噪声环境为高斯白噪声;Monte Carlo试验次数为500。
起始频率及调制斜率估计性能如图2所示。由于分步估计算法在2 dB以上信噪比时估计误差收敛,根据2.1节的分析可知,该理论界在噪声收敛时可近似作为估计下限。
由图2可知,在2~10 dB信噪比范围内,起始频率估计的标准差约为5~12倍的MCRLB,调制斜率估计的NRMSE约为2~4倍的MCRLB。假设参数的CRLB可以得到,则根据式(16),其应位于分步估计近似下限曲线与MCRLB曲线之间,因此可以推测此时的起始频率与调制斜率估计的MCRLB已经接近CRLB。
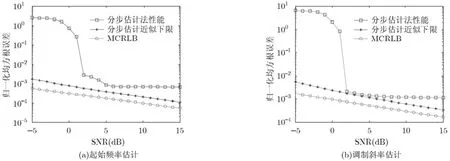
图 2 参数估计性能对比
码元宽度估计结果如图3所示。由图3可知,分步算法的码元宽度估计的标准差约为10~20倍的MCRLB。同理,由于经典的CRLB应位于MCRLB与分步算法性能曲线之间,可以推测此时复合信号码元宽度估计的MCRLB已经接近于CRLB。

图 3 码元宽度估计性能
另一方面,也可以看出分步估计算法估计性能在信噪比高于2 dB时趋于稳定。这和文献[7]中分步估计算法选用的参数设置有关。在起始频率和调制斜率估计时,使用了FFT系数迭代插值算法,其迭代终止条件导致了算法的固有误差。而码元宽度估计时使用了常规的自相关算法和求倒数运算,其估计精度也有一定误差。故算法参数的设置和子算法的选取导致误差下降到一定程度后,算法性能随着信噪比的提升基本维持不变。
从理论分析和仿真实验可以看出,复合信号参数估计的MCRLB作为估计算法的性能评价工具是合理和有效的。另一方面,目前PRBC-LFM复合信号参数的分步估计方法尚存在两方面的问题:一方面在信噪比低于2 dB时如何使算法估计误差快速收敛上没有文献涉及;另一方面,在高信噪比时分步估计方法的理论性能与白噪声中参数无偏估计的修正理论下限仍有一定偏离。
5 结束语
针对PRBC-LFM复合信号参数估计的性能分析问题,从理论角度定量分析了分步估计方法的理论性能,并通过合理假设,首次导出了该复合信号参数联合估计的修正Fisher信息矩阵,在此基础上得到了各参数估计的修正的克拉美-罗下限,通过数值仿真试验对比了已有文献的估计结果,证明了所得理论下限的有效性和合理性,为伪码-线性调频复合信号的参数估计方法性能评价提供了一种理论工具。寻找更低信噪比下的参数有效估计方法及高信噪比时误差更小的参数估计方法是后续有待开展的工作。
参考文献
[1]LYNCH David Jr.Introduction to RF Stealth[M].Releigh,NC:SciTech Publishing,2004:336-343.
[2]NGWAR M and WIGHT J.Phase coded linear frequency modulated waveform for low cost marine radar system[C].IEEE Radar Conference,Washington,DC,2010:1044-1049.doi:10.1109/RADAR.2010.5494447.
[3]RENSEAU J and ADHAMI Reza R.Phase-coded LFMCW waveform analysis for short range measurement applications[C].IEEE Aerospace Conference,Big Sky,MT,2014:1-6.doi:10.1109/AERO.2014.6836285.
[4]KOWATSCH M and LAFFERI T J.A spread-spectrum concept combining chirp modulation and pseudo-noise coding[J].IEEE Transactions on Communications,1983,31(10):1133-1142.doi:10.1109/TCOM.1983.1095745.
[5]周新刚,赵惠昌,刘风格,等.伪码调相与线性调频复合调制引信[J].宇航学报,2008,29(3):1026-1030.doi:10.3873/ j.issn.1000-1328.2008.03.055.ZHOU Xingang,ZHAO Huichang,LIU Fengge,et al.Pseudorandom code binary phase modulation combined with linear frequency modulation fuze[J].Journal of Astronautics,2008,29(3):1026-1030.doi:10.3873/j.issn.1000-1328.2008.03.055.
[6]熊刚,杨小牛,赵惠昌.基于平滑伪Wigner分布的伪码与线性调频复合侦察信号参数估计[J].电子与信息学报,2008,30(9):2115-2119.doi:10.3724/SP.J.1146.2007.00205.XIONG Gang,YANG Xiaoniu,and ZHAO Huichang.Parameter estimation of reconnaissance signal combined PN and LFM based on smoothed pseudo Wigner distribution[J].Journal of Electronics & Information Technology,2008,30(9):2115-2119.doi:10.3724/SP.J.1146.2007.00205.
[7]曾德国,熊辉,龙柯宇,等.伪码-线性调频复合信号快速参数估计方法[J].系统工程与电子技术,2010,32(5):891-894.doi:10.3969/j.issn.1001-506X.2010.05.003.ZENG Deguo,XIONG Hui,LONG Keyu,et al.Fast parameter estimation approach of reconnaissance signal combined PRBC and LFM[J].Systems Engineering and Electronics,2010,32(5):891-894.doi:10.3969/j.issn.1001-506X.2010.05.003.
[8]薛妍妍,刘渝.LFM-BPSK复合调制信号识别和参数估计[J].航天电子对抗,2012,28(1):60-64.doi:10.3969/j.issn.1673-2421.2012.01.022.XUE Yanyan and LIU Yu.The recognition and parameter estimation of LFM-BPSK[J].Aerospace Electronic Warfare,2012,28(1):60-64.doi:10.3969/j.issn.1673-2421.2012.01.022.
[9]刘勇,张国毅,胡鑫磊.伪码-线性调频复合信号的参数估计[J].航天电子对抗,2014,30(4):22-25.doi:10.3969/j.issn.1673-2421.2014.04.007.LIU Yong,ZHANG Guoyi,and HU Xinlei.Parameter estimation of reconnaissance signal combined PN and LFM[J].Aerospace Electronic Warfare,2014,30(4):22-25.doi:10.3969/j.issn.1673-2421.2014.04.007.
[10]崔伟亮,江桦,李剑强,等.改进的循环谱估计快速算法与性能分析[J].电子与信息学报,2011,33(7):1594-1599.doi:10.3724/SP.J.1146.2010.01170.CUI Weiliang,JIANG Hua,LI Jiangqiang,et al.Improved fast cyclic spectral estimation algorithm and performance analysis[J].Journal of Electronics & Information Technology,2011,33(7):1594-1599.doi:10.3724/SP.J.1146.2010.01170.
[11]马秀荣,曹多.基于功率谱离散余弦变换的BPSK信号参数估值[J].电子与信息学报,2014,36(9):2075-2080.doi:10.3724/SP.J.1146.2013.01756.MA Xiurong and CAO Duo.Parameters estimation of BPSK signals based on power spectral DCT[J].Journal of Electronics & Information Technology,2014,36(9):2075-2080.doi:10.3724/SP.J.1146.2013.01756.
[12]D’ANDREAA N,MENGALI U,and REGGIANINI R.The modified Cramer-Rao bound and its application to synchronization problems[J].IEEE Transactions on Communications,1994,42(2/3/4):1391-1399.doi:10.1109/ TCOMM.1994.580247.
[13]GINI F,REGGIANINI R,and MENGALI U.The modified Cramer-Rao bound in vector parameter estimation[J].IEEE Transactions on Communications,1998,46(1):52-60.doi:10.1109/26.655403.
[14]邓振淼,刘渝.相位编码信号码元宽度估计的修正克拉美-罗限[J].通信学报,2009,30(9):117-121.doi:10.3321/j.issn:1000-436X.2009.09.017.DENG Zhenmiao and LIU Yu.Modified Cramer-Rao lower bound for symbol width estimation from a phase-shift-keying signal[J].Journal on Communications,2009,30(9):117-121.doi:10.3321/j.issn:1000-436X.2009.09.017.
[15]POLLOK A and MCKILLIAM R.Modified Cramér-Rao bounds for continuous-phase modulated signals[J].IEEE Transactions on Communications,2014,62(5):1681-1690.doi:10.1109/TCOMM.2014.030814.130804.
[16]GOGINENI S,RANGASWAMY M,RIGILING D,et al.Cramér-Rao bounds for UMTS-based passive multistatic radar[J].IEEE Transactions on Signal Processing,2014,62(1):95-106.doi:10.1109/TSP.2013.2284758.
[17]WANG Pei,DU Dongping,QIU Zhaoyang,et al.Modified Cramer-Rao bounds for parameter estimation of hybrid modulated signal combining PRBC and LFM[C].IEEE 17th International Conference on Computational Science and Engineering(CSE),Chengdu,2014:1029-1033.doi:10.1109/ CSE.2014.204.
[18]LIUBISA S,MILOS D,and THAYANANTHAN T.Timefrequency Signal Analysis with Applications[M].Norwood,MA:Artech House,2013:428-428.
[19]熊竹林,刘策伦,安建平.一种低复杂度线性调频信号参数估计算法[J].电子与信息学报,2015,37(2):489-493.doi:10.11999/JEIT140166.XIONG Zhulin,LIU Celun,and AN Jianping.A low complexity parameter estimation algorithm of LFM signals[J].Journal of Electronics & Information Technology,2015,37(2):489-493.doi:10.11999/JEIT140166.
王佩:男,1988年生,博士生,从事雷达信号侦察方面研究.
祝俊:男,1974年生,博士后,从事电子对抗方面研究.
唐斌:男,1963年生,教授,博士生导师,主要从事电子对抗与雷达抗干扰技术方面研究.
Theoretical Performance Analysis for Parameter Estimation of Hybrid Modulated Signal Combining Pseudo-random Binary-phase Code and Linear Frequency Modulation
WANG PeiZHU JunTANG Bin
(School of Electronic Engineering,University of Electronic Science and Technology of China,Chengdu 611731,China)
Abstract:According to the theoretical performance for parameter estimators of a signal combined Pseudo-Random Binary-phase Code(PRBC)and Linear Frequency Modulation(LFM),this paper analyzes the impact of step-bystep method on the signal estimation problem and gives the analytical expressions of Modified Cramer-Rao Lower Bound(MCRLB)for parameter estimation of PRBC-LFM signal in white Gaussian noise.Using the statistical characteristics of PRBCs,the Fisher’s information matrix is derived for parameters including initial frequency,chirp rate,initial phase and code width.The MCRLBs are therefore calculated.The MCRLBs are analyzed by comparison and the validity is demonstrated by numerical simulation experiments.
Key words:Parameter estimation; Pseudo-Random Binary-phase Code and Linear Frequency Modulation(PRBCLFM)signal; Step-by-step estimation method; Modified Cramer-Rao Lower Bound(MCRLB)
基金项目:国家自然科学基金(61172116)
*通信作者:王佩wangpei1128@foxmail.com
收稿日期:2015-05-06;改回日期:2015-10-09;网络出版:2015-11-18
中图分类号:TN971.+1
文献标识码:A
文章编号:1009-5896(2016)02-0472-06
DOI:10.11999/JEIT150523
Foundation Item:The National Natural Science Foundation of China(61172116)
