模糊数学在超声波检测桩基完整性中的应用
2016-04-20陈向阳王志鑫
陈向阳,王志鑫
(长沙理工大学,湖南长沙 410004)
模糊数学在超声波检测桩基完整性中的应用
陈向阳,王志鑫
(长沙理工大学,湖南长沙 410004)
摘要:现有规范对于桩基完整性的评判过于简单,所用方法过于笼统,而且对于有些桩基的完整性很难准确判定。文中根据超声波透射法检测桩基所得波速、波幅和波形,利用模糊数学对桩基完整性进行分析,以准确判断桩基的完整性。
关键词:桥梁;桩基;超声波;模糊数学;完整性
目前,在超声波透射法检测中,在利用接收器接收的信号确定缺陷的有无、大小、形状和性质时常会遇到这样的问题,即缺陷信号与散射波信号之间及不同类型缺陷信号之间的特征比较模糊,很难对它们作出十分精确的判断。
作为隐蔽工程,桩基础一般在地下或水下,具有技术要求高、工序繁杂、施工难度大等特点,在施工过程中很容易出现质量问题,对于桩基的检测研究尤为重要。运用超声波检测桩基时,一般采用波速、波幅和PSD(功率谱密度)值进行桩身完整性判断,由于对导致异常声测曲线的缺陷的大小、性质判断不精确,很难对桩基完整性进行精确判别。为此,该文运用模糊数学对超声波桩基检测中出现的较模糊的缺陷作出判别。
1 基于模糊数学的桩基完整性判别
除波速、波幅外,波形也能直观地反映桩基的完整性,波形畸变的厉害程度与桩基质量有一定关系。因此,应用模糊数学建立的评判因素集为{波速,波幅,波形}。波速、波幅、波形对于判断桩基检测完整性有不同程度的影响,赋予相应权重为A={0.6,0.3,0.1}。
1.1 隶属度函数确定
常用的隶属度函数有偏大型、中间型和偏小型3种。在桩基检测中,优秀的采用偏大型,合格的采用一般型,不合格的采用偏小型。其函数形式,偏大型为:

中间型为:
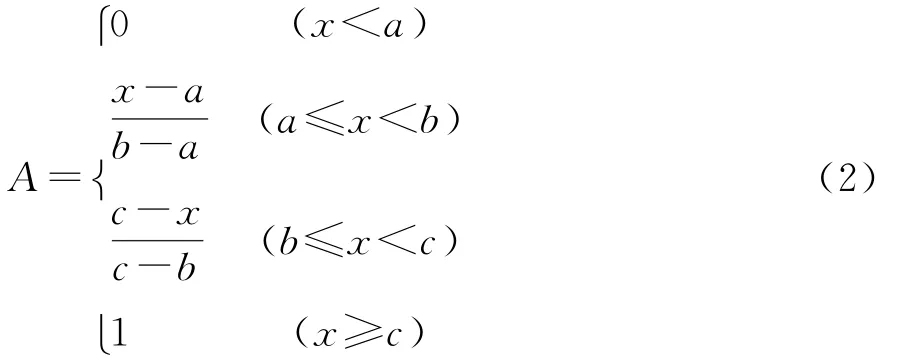
偏小型为:

1.2 置信区间的划分
在超声波桩基检测中,通过发射器发出的波速在不同介质中的传播速度不同,从而不同程度地反映桩基的质量。因此,波速通常作为判断桩基完整性的主要参数之一。波速临界值是界定波速是否异常的参照值,可根据临界值确定波速的置信区间。波速临界值vc=vm-2σv(vm为波速平均值,σv为波速标准差)。取a=vm-2σv,b=vm,c=vm+ 2σv。
波幅的大小是声波在传播中衰减程度的具体体现。超声波在砼中传播的衰减情况可由波幅测值的变化直接反映,并且波幅遇到缺陷时突变明显进而反映桩基的质量。因此,波幅可用于判断桩基的完整性。不过波幅容易受仪器性能、换能器耦合情况、测距等非缺陷因素的影响,故不可单凭波幅情况进行判别。波幅临界值是界定波幅是否异常的参照值,可根据临界值确定波幅的置信区间。波幅临界值Ac=Am-6(Am为波幅平均值)。取a=Am-6,b=Am,c=Am+6。
波形对于判断桩基完整性有参考作用,波速和波幅也从侧面影响波形的好坏。当超声波在有缺陷的砼中传播时,缺陷的复杂界面使其传播路径复杂化,产生绕射、反射、折射等,最后形成一个波形畸变的超声波信号,波形畸变越厉害则砼缺陷越严重。波形的好坏可反映桩基的质量,但波形易受非缺陷因素的影响,只能作为辅助参考。波形的置信函数不是通过计算得到,而是通过综合分析确定。
1.3 模糊评判分析
采用超声波的波速、波幅和波形作为评判因素域,即U={波速,波幅,波形},评判论域V={优秀,合格,不合格},则模糊关系矩阵R=U×V。根据赋予的权重和模糊矩阵得出综合评判矩阵B=A· R,由此判断桩基缺陷的有无及程度。
2 实例分析
2.1 超声波检测结果
某桥梁桩基长度为7.4 m,直径为1.2 m,采用C25砼。设置3根声测管,检测仪器为RSM -SY6。1-2剖面0~4 m处的检测数据见表1。

表1 0~4 m的检测数据
1-2剖面跨距为850 mm,波速平均值vm= 4.460 km/s,波幅平均值Am=102 dB;标准差:σv=0.065,σA=3.9;临界值:vc=4.33 km/s,Ac=96 d B。通过表1可以看出:2.4~2.8 m处波速、波幅明显偏低,该范围存在缺陷。
2.2 桩基完整性模糊评判
利用模糊数学分析该桩基,分别计算2.0、2.6 m两个测点处的模糊矩阵,对其完整性进行评价。
2.2.1 求波速的隶属函数
把波速的平均值vm=4.460 km/s、标准差σv= 0.065、临界值vc=4.33 km/s带入式(1)~(3),得优秀的波速的隶属函数为:

合格的隶属函数为:

不合格的隶属函数为:

在深度2.0 m处,波速v=4.57 km/s,带入式(4)~(6),得到2.0 m处波速的隶属函数为U1× V1=(0.85,0.15,0)。在深度2.6 m处,波速v= 4.067 km/s,带入式(4)~(6),得到2.6 m处波速的隶属函数为u1×v1=(0,0,1)。
2.2.2 求波幅的隶属函数
同理,把波幅的平均值、标准差、临界值带入式(1)~(3),得优秀的波幅的隶属函数为:

合格的隶属函数为:

不合格的隶属函数为:

在深度2.0 m处,波幅A=100.6 dB,带入式(7)~(9),得到2.0 m处波幅的隶属函数U2×V2=(0,0.77,0.23)。在深度2.6 m处,波幅A=93 dB,带入式(7)~(9),得到2.6 m处波幅的隶属函数u2×v2=(0,0,1)。
2.2.3 求波形的隶属函数
超声波检测得到的2.0、2.6 m处波形分别见图1、图2。
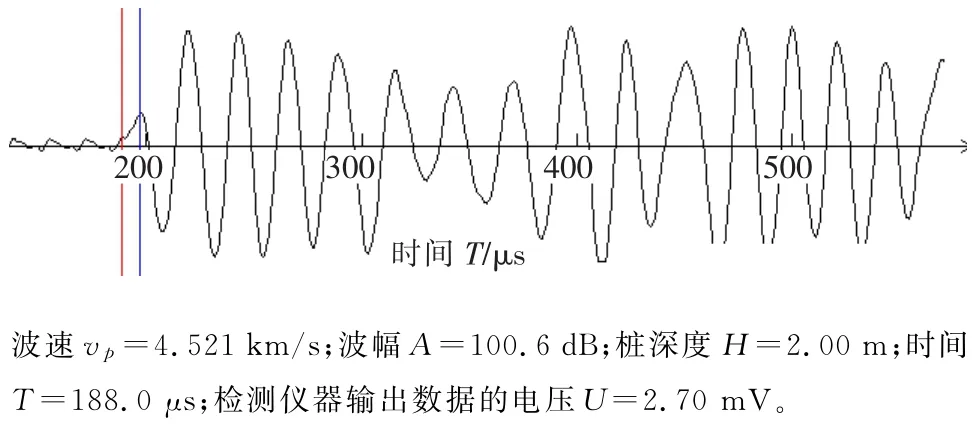
图1 2.0 m处第10个测点的检测波形

图2 2.6 m处第13个测点的检测波形
分析图1、图2所示波形,2.0 m处波形首波陡峭,波幅高,第一个周期的后半周达到较高振幅,波形无畸变,确定隶属函数U3×V3=(0.8,0.2,0); 2.6 m处波形首波平缓,波幅小,向后延迟,第一个周期的后半周和第二周期波幅仍小,波形有畸变,确定隶属函数u3×v3=(0,0.1,0.9)。
2.2.4 模糊评判分析
根据上述分析结果,在深度2.0 m处,波速的隶属函数为U1×V1=(0.85,0.15,0),波幅的隶属函数为U2×V2=(0,0.77,0.23),波形的隶属函数为U3×V3=(0.8,0.2,0),从而得2.0 m测点处的模糊矩阵为:

在深度2.6m处,波速的隶属函数为u1×v1=(0,0,1),波幅的隶属函数为u2×v2=(0,0,1),波形的隶属函数为u3×v3=(0,0.1,0.9),得2.6 m测点处的模糊矩阵为:

从而得到深度2.0、2.6 m处的综合评判矩阵分别为:

根据评判结果,2.0 m测点处该剖面为优秀,2.6 m测点处该剖面为不合格,与实测结果一致。
3 结语
该文采用的模糊综合判定方法充分考虑了影响砼质量评价中的各声学参数,从实例计算结果来看,利用该评价方法可准确判断桩基完整性,得出的结果与实际工程相符,对于判断桩身是否存在缺陷具有较好的可靠性。
参考文献:
[1]JGJ 106-2003,建筑基桩检测技术规范[S].
[2]杨纶标,高英仪.模糊数学原理及应用[M].广州:华南理理工大学出版社,2004.
[3]JTG/T F81-01-2004,公路工程基桩动测技术规程[S].
[4]陈国栋.超声波在混凝土桩基础无损检测中的应用研究[D].武汉:武汉理工大学,2005.
[5]马溁.超声波透射法在桥梁桩基完整性检测中的应用[J].公路与汽运,2014(6).
[6]罗开玉,苏柏,吕刺,等.7075-T6铝合金激光对接焊质量的超声波探伤测试与分析[J].激光与光电子学进展,2013(6).
[7]张增赞,李微,崔杰.声波透射法在桥梁基桩质量检验中的应用[J].西部探矿工程,2003,15(1).
[8]柴国平.超声波透射法在桥梁基桩完整性检测中的研究[J].甘肃水利水电技术,2014,50(12).
[9]孙志朋.浅析声波透射法在桥梁基桩桩身完整性检测中的应用[J].建筑工程技术与设计,2015(16).
收稿日期:2015-03-07
中图分类号:U446.2
文献标志码:A
文章编号:1671-2668(2016)02-0205-03
