基于驾驶模拟的汽车ABS仿真研究
2016-04-20熊登熊坚陈启帆
熊登,熊坚,陈启帆
(昆明理工大学交通工程学院,云南昆明 650500)
基于驾驶模拟的汽车ABS仿真研究
熊登,熊坚,陈启帆
(昆明理工大学交通工程学院,云南昆明 650500)
摘要:采用一种汽车防抱死制动系统(ABS)双逻辑门限值控制策略,通过驾驶模拟器程序控制和驾驶员在环仿真试验,比较分析程序控制和驾驶员控制对ABS算法的影响。试验结果表明,在给定控制算法下,程序驾驶控制和驾驶员在环驾驶控制都能使车轮的滑移率控制在20%左右,但驾驶员控制下车轮滑移率的波动更大,其原因为该环境下驾驶员可根据自己的判断实时调整操作,操作数据随机性更强,更符合实际情况。
关键词:汽车;防抱死制动系统(ABS);驾驶模拟器;双逻辑门限值控制;程序控制仿真;驾驶员在环仿真
汽车防抱死制动系统(ABS)常用控制方法有模糊控制、PID(比例、积分、微分)控制、神经网络控制、滑动模态结构控制和逻辑门限值控制等,其中逻辑门限值控制应用最普遍,其优点是在没有具体系统的数学模型下就能对ABS系统进行有效的非线性控制。使用该控制方法时,只需利用汽车在制动过程中车轮角减速度门限值控制就能实现基本的防抱死制动循环,若再附加车轮滑移率门限值作为辅助门限则会产生更佳的控制效果。
在以往的仿真研究中,驾驶输入都是采用程序控制的方法,该方法方便、简单,通过仿真研究,基本能检验ABS的控制算法。但汽车的ABS最终是要安装在实际车辆上,并且是在特殊环境下由人来操纵控制,这与传统仿真研究的程序控制是有区别的。该文采用ABS双逻辑门限值控制算法,通过驾驶模拟器,对汽车ABS在程序控制和驾驶员在环仿真控制下的该算法进行仿真试验,分析两种方法的差异及产生原因。
1 车辆模型的建立
为了方便ABS建模,选用双轮三自由度车辆模型。该模型的特点在于忽略了侧向力的变化,同时利用纵向魔术公式可准确描述单一工况下制动过程中轮胎的受力及运动状况。
1.1 车辆动力学模型
车辆制动过程中的受力如图1所示。
车辆运动方程为:


图1 制动过程中车辆受力示意图
式中:m为汽车质量;t为制动时间。
垂直载荷为:
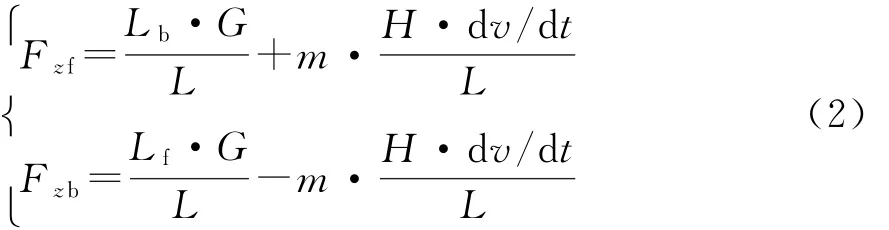
车轮的运动方程为:

式中:J为车轮转动惯量;dω/d t为车轮减速度。
滑移率S的计算公式为:

1.2 轮胎模型
采用魔术公式轮胎模型,该模型只用一套公式即可完整地表达纯工况下轮胎的力学特性。
根据魔术公式的一般表达式,在纯制动单一工况下,轮胎纵向力F与纵向滑移率S和垂直载荷Fz的关系为:
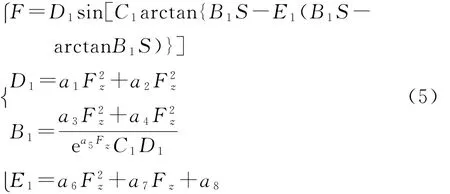
式中:D1为峰值因子;C1为曲线形状因子;B1为刚度因子;E1为曲线曲率因子;a1、a2、a3、a4、a5、a6、a7、a8均为曲线拟合参数。
为了适应不同附着系数的路面,将附着系数通过曲线拟合的方式引入魔术公式,通过MATLAB进行拟合,得到a2与附着系数φ的关系为:

2 ABS双逻辑门限值控制流程
ABS双逻辑门限值控制算法中需参考的门限值只有2个,即车轮角减速度门限值a1和滑移率门限值S1,比传统逻辑门控制算法的4个控制参数少,因而这种控制算法逻辑简单,控制步骤较少,更适合于仿真分析。其逻辑关系如图2所示。
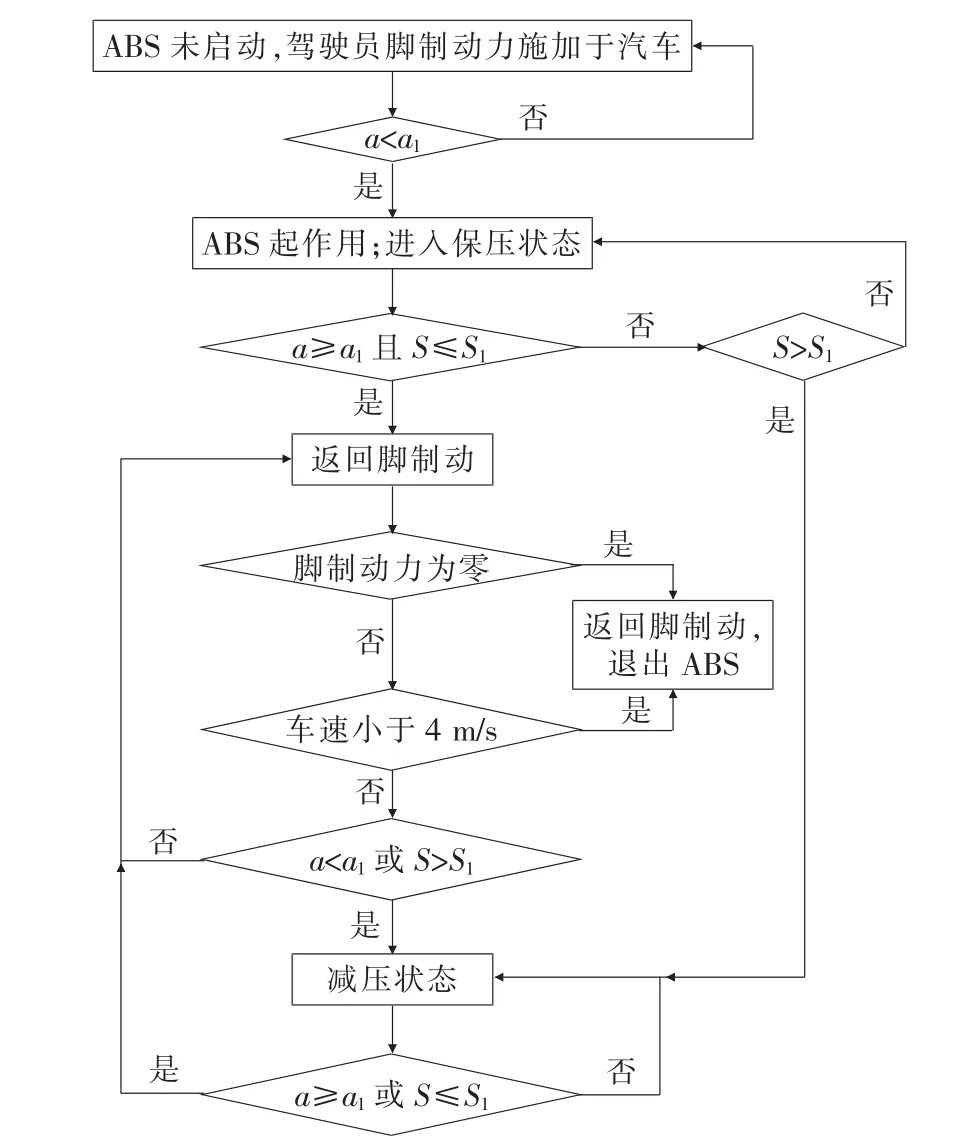
图2 ABS双逻辑门限值控制算法的控制逻辑
该算法的控制流程为:
第一次循环过程中,制动初期,ABS不工作,当检测到车轮角减速度a<a1时,ABS开始工作,驾驶员制动不再起作用,系统进入保压阶段。在保压阶段进行两次判断,如果车轮角减速度a≥a1且滑移率S≤S1,则ABS不工作,系统进入第二次循环中的驾驶员制动状态;如果不满足前面的情况,但滑移率S>S1,则说明处于低附着系数路面,ABS系统进入第二次循环中的减压状态;如果两种情况都不满足,则维持保压状态,直到出现两种情况中的一种,再进入ABS系统的第二次循环。
第二次循环过程中,如果以驾驶员制动作为循环的起始点,需先对制动力和车速进行判断。如果脚制动力为零或车速小于4 m/s,则退出ABS,返回未进入ABS时的初始阶段。若不满足上面的情况,则维持驾驶员制动状态,直到车轮角减速度a<a1或滑移率S>S1时,ABS系统进入减压状态。在减压状态过程中,当检测到车轮角减速度a≥a1或滑移率S≤S1时,则返回驾驶员制动状态,接着继续循环,直到车辆停止。
3 驾驶模拟仿真试验
驾驶模拟仿真试验在小型模拟器上完成(如图3所示)。先在MATLAB中建立式(1)~(6)的车辆模型和图2所示逻辑控制模块,其中车辆模型中的参数设定参考捷达车的各项参数,然后将所建ABS控制模块生成C语言程序源代码,最后将C语言程序代码导入KMRTS车辆动力学模型中进行仿真试验。

图3 小型驾驶模拟器
驾驶模拟仿真试验分为驾驶模拟器的程序控制仿真试验和驾驶员在环ABS仿真试验。驾驶模拟器程序控制仿真试验则是在动力学模型中设置一定的程序信号(如制动踏板行程、制动开始时间、制动停止时间、方向盘转角等)控制整个仿真过程,最后将各控制参数依次输入驾驶模拟器的动力学模型中;驾驶员在环ABS仿真试验则是通过驾驶员在模拟器上实际驾驶,采集操纵信号来进行相关参数的数据分析。
3.1 程序控制仿真试验
为了通过程序控制仿真达到验证汽车ABS有效性的目的,设定紧急制动避障场地(如图4所示)。车辆以一定的初始速度从起始处出发,当距离障碍物30 m时,紧急制动并给方向盘一定的转角来避开障碍物,根据前后轮的滑移率和车速变化情况及行驶状态俯览图,分析车辆ABS的有效性。
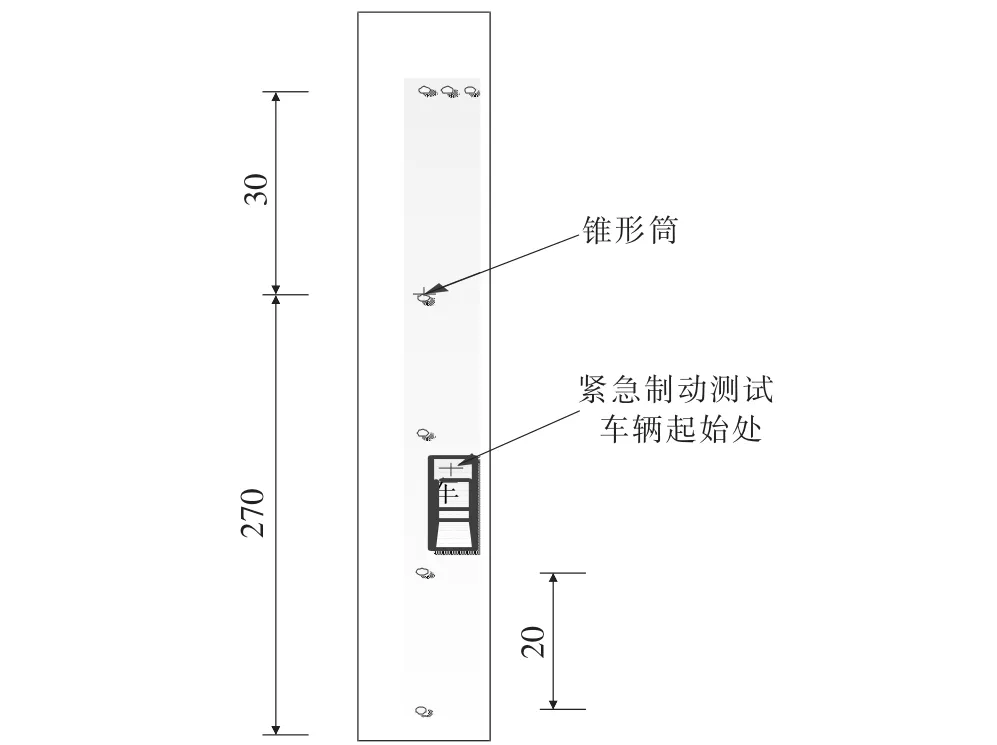
图4 紧急制动避障试验场景俯览示意图(单位:m)
程序控制仿真试验在高附着系数(0.8)路面上进行。试验时,初始车速为80 km/h,仿真步长为0.01 s。图5为程序控制下的仿真曲线。
从图5(a)可以看出:在ABS程序控制的情况下,车辆突然进行紧急制动,车轮没有完全抱死,成功避开了障碍物,进入草地中,没有发生甩尾现象,整个制动过程中车辆保持了良好的操纵稳定性。
从图5(b)可以看出:车轮速度均匀波动下降,变化趋势较好,没有发生抱死现象。
从图5(c)可以看出:左前轮、左后轮滑移率均稳定在0.2左右,前后车轮均未抱死,说明该控制策略有效,能满足汽车ABS的控制需求。
3.2 驾驶员在环ABS仿真试验
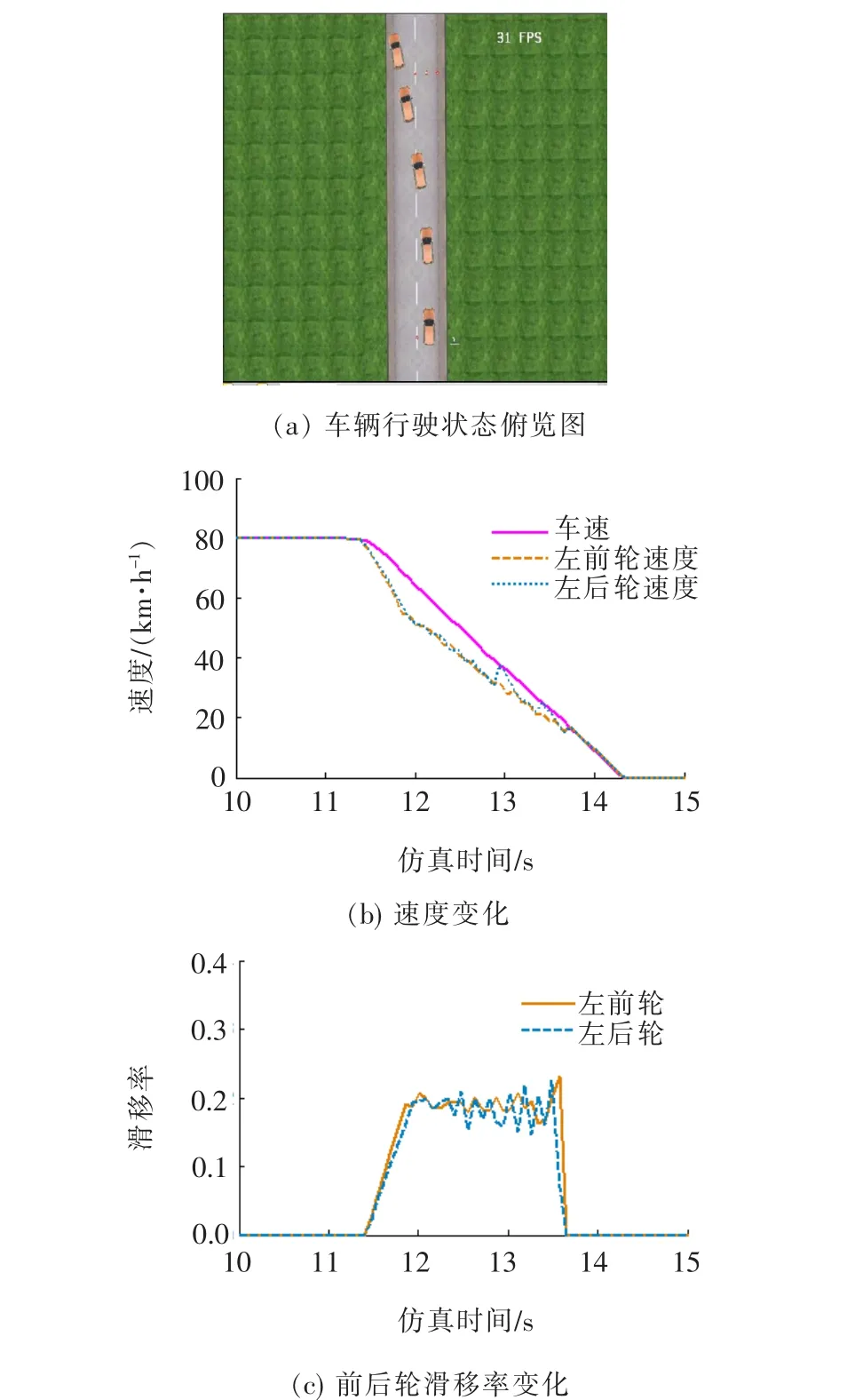
图5 紧急制动避障过程中ABS程序控制仿真曲线
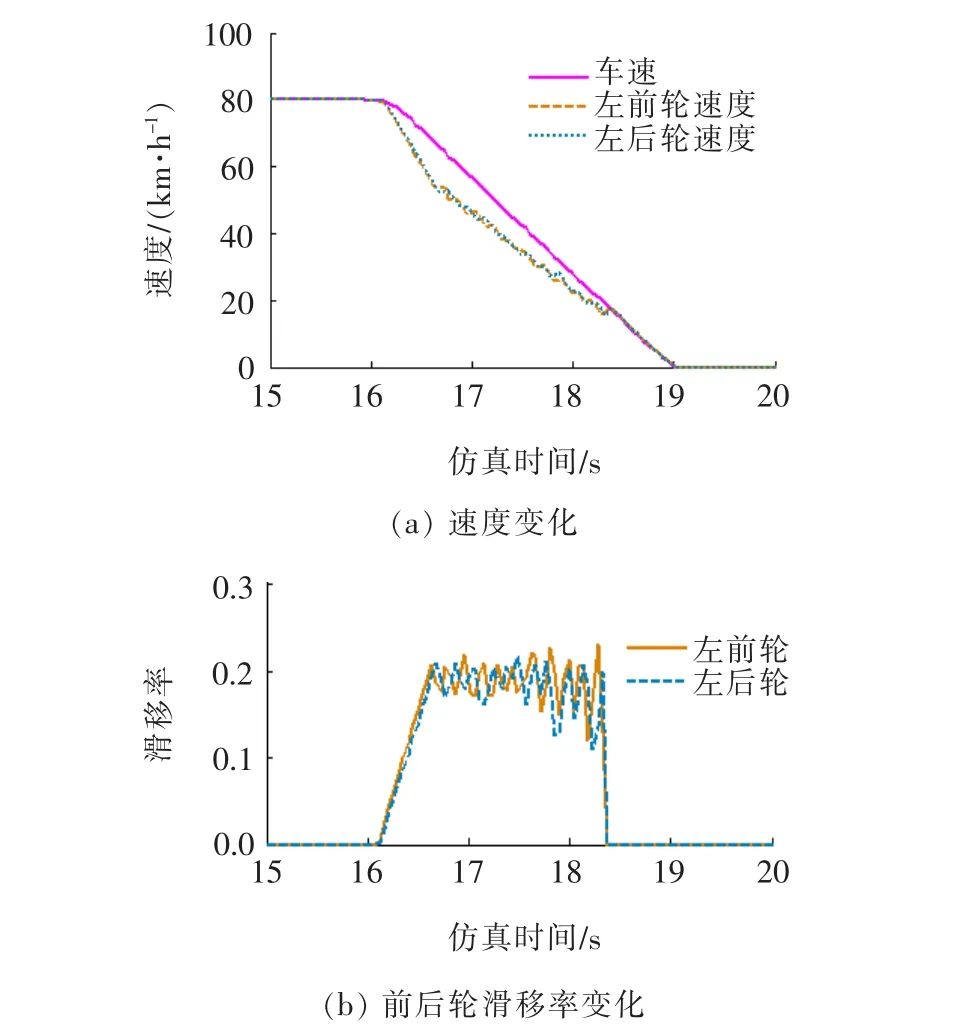
图6 驾驶员在环仿真车辆动力学参数曲线
驾驶员在环仿真试验所用试验场景与程序控制仿真试验场景相同,不同的是试验过程由程序控制改为驾驶员实际操作,通过采集驾驶员的相关操纵信号进行数据分析。图6为驾驶员操控在高附着系数路面进行仿真试验所采集的部分车辆动力学参数。
从图6可以看出:在驾驶员控制的情况下,在仿真时间为16 s时,车轮速度开始均匀波动下降,前后轮滑移率开始急剧上升,且在整个制动过程中两车轮滑移率控制在0.2左右,车轮都没有抱死,说明这套ABS控制系统在驾驶员实际操作时能满足控制需要。
3.3 程序控制仿真与驾驶员在环仿真对比分析
程序控制仿真试验与驾驶员在环仿真试验在实际操作过程及仿真结果中存在一定的区别,下面对高附着系数路面上两试验的滑移率和操作行为参数进行对比分析。
两个试验在高附着系数路面下的滑移率变化分别如图5(c)、图6(b)所示。从中可以看出:无论是程序控制还是驾驶员操作,在整个制动过程中车轮滑移率均稳定在0.2左右,处于良好控制范围内,说明采用的双逻辑门限值控制策略能满足汽车ABS的控制需求,在驾驶模拟器仿真中是有效的;但程序控制下滑移率的振动频率和幅度较小,过于理想化,而驾驶员操控下得到的滑移率变化幅度更大,更符合实际制动过程。
图7、图8分别为程序控制和驾驶员控制下的操作行为参数曲线。
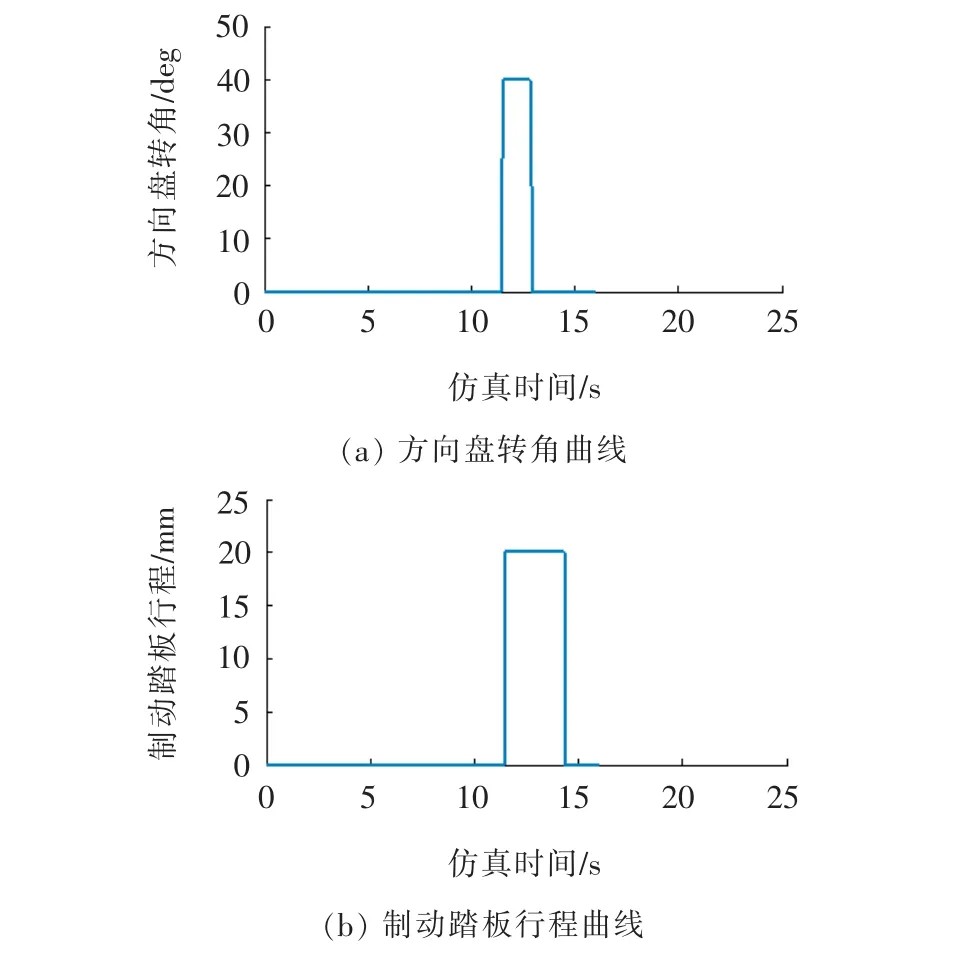
图7 程序控制下的操作行为参数曲线
从图7来看,在程序控制下,方向盘转角与脚踏板行程都非常稳定,不存在抖动现象。从图8来看,方向盘转角比较稳定,偶尔会有小幅度的变化,在整个制动过程中,制动踏板行程变化也较平稳,属于稳定踩死刹车之后松开刹车的制动过程。对比两图可以发现,在驾驶员控制下,驾驶员可根据自己的判断实时调整操作,操作数据随机性更强,更符合实际情况,更适合用来检测ABS的控制效果。
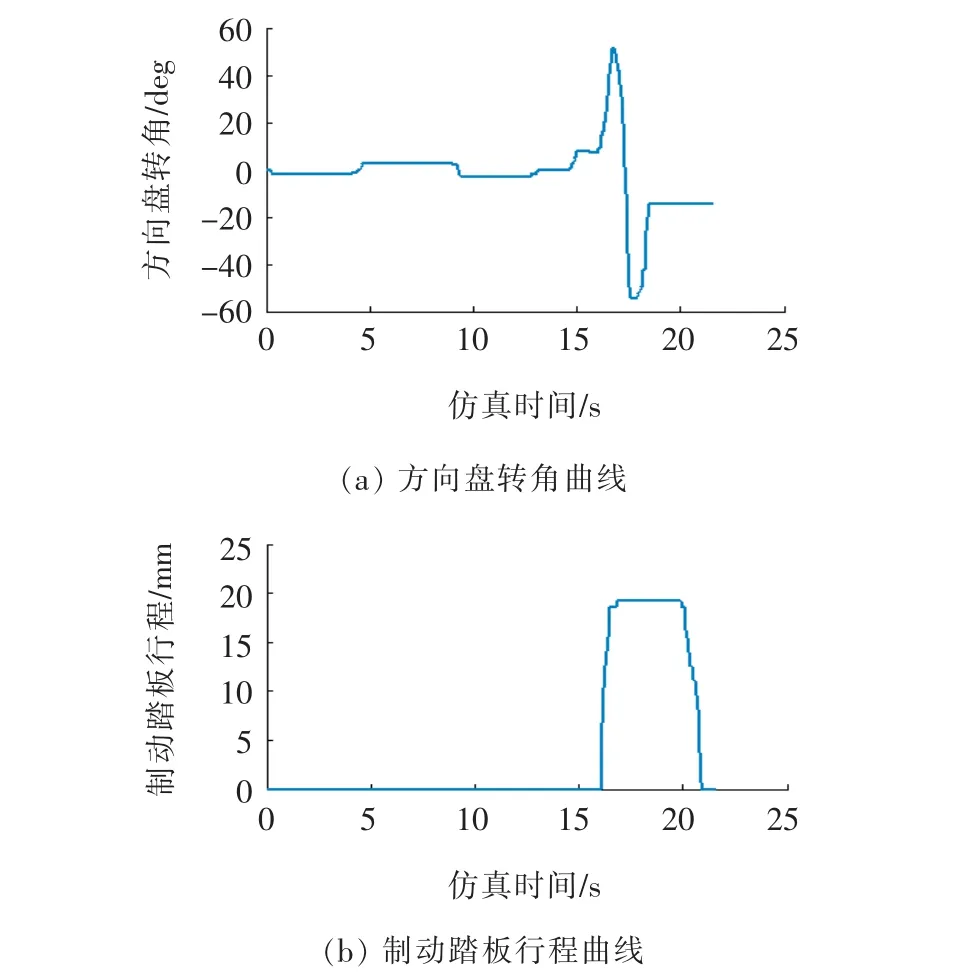
图8 驾驶员控制下的操作行为参数曲线
4 结论
该文在传统逻辑门限值控制策略的基础上提出了一种双逻辑门限值的汽车ABS控制策略,采用驾驶模拟器对该控制策略分别进行程序控制仿真试验和驾驶员在环ABS仿真试验,通过滑移率和操作行为参数对比两种仿真试验的区别。通过对试验仿真结果的分析,主要得到以下结论:
(1)在汽车ABS双逻辑门限值控制算法下,程序驾驶控制和驾驶员在环驾驶控制都能使车轮的滑移率控制在0.2左右,但在驾驶员控制下车轮滑移率的波动范围更大,更符合实际的制动过程。
(2)驾驶员在环驾驶控制时,驾驶员可根据自身判断实时调整操作,操作数据随机性更强,更符合实际情况,更适合用来检测汽车ABS的控制效果。
参考文献:
[1]李韶华,黄宏伟,李灿.基于虚拟样机技术的重型汽车ABS模糊控制研究[J].科技导报,2013,31(4).
[2]席本强,何毅,丘文森.汽车ABS的模糊自适应PID控制[J].辽宁工程技术大学学报,2014,33(11).
[3]刘鑫伟,谷正气,杨易,等.基于模糊神经网络的汽车辅助制动控制系统的研究[J].汽车工程,2010,32(12).
[4]潘辉,李礼夫.基于路面识别的汽车ABS滑模控制方法的研究[J].现代制造工程,2011(2).
[5]王伟达,丁能根,张为,等.ABS逻辑门限值自调整控制方法研究与试验验证[J].机械工程学报,2010,46(22).
[6]郑太雄,马付雷.汽车ABS逻辑门限值控制方法研究[J].重庆邮电大学学报,2011,23(4).
[7]郑太雄,马付雷.基于逻辑门限值的汽车ABS控制策略[J].交通运输工程学报,2010,10(2).
[8]田晶晶,阳冬波,李枭.基于遗传算法的魔术公式轮胎模型参数辨识方法研究[J].交通节能与环保,2014(4).
[9]Pacejka H B.Tyre and vehicle dynamics[M].Oxford: Butterworth-Heinemann,2006.
[10]梁春兰,盛鹏程,刘卫泽.基于“魔术公式”轮胎模型的MATLAB仿真研究[J].邢台职业技术学院学报,2013,30(1).
[11]陈启帆.驾驶员在环汽车ABS仿真实验研究[D].昆明:昆明理工大学,2014.
收稿日期:2015-12-09
中图分类号:U463.52
文献标志码:A
文章编号:1671-2668(2016)02-0011-04
