等高度连续梁桥偏载系数计算和试验研究
2016-04-20周广利彭汉杰巩文龙渠广镇
周广利,彭汉杰,巩文龙,渠广镇,2
(1.山东省交通科学研究院,山东济南 250031;2.长安大学公路学院,陕西西安 710054)
等高度连续梁桥偏载系数计算和试验研究
周广利1,彭汉杰1,巩文龙1,渠广镇1,2
(1.山东省交通科学研究院,山东济南 250031;2.长安大学公路学院,陕西西安 710054)
摘要:在连续箱梁设计中,引入偏载系数能将空间计算问题简化为梁单元计算问题。文中通过对某等高度连续梁桥偏载试验数据的分析,将传统简化计算方法、有限元法计算的偏载系数与实测值进行对比,结果表明,传统简化计算方法的结果与实测值存在较大偏差,而有限元法计算的偏载系数与实测值吻合,有限元法计算的偏载系数最符合工程实际,宜优先采用。
关键词:桥梁;连续梁桥;偏载系数;有限元
在桥梁设计计算和荷载试验中,荷载横向分布计算十分重要。对于空心板梁桥、T梁桥等拼装式结构,横向分布系数能有效地将空间问题简化成对单梁的设计和计算问题。横向分布计算方法主要有铰接板法、偏心压力法、刚接梁法等,这些方法已在实际工程应用中证明了其适用性,参数取值也相对成熟。而对于连续梁桥,特别是中等跨径的宽幅连续梁桥,由于双向受力效应明显,荷载的横向分布更复杂,设计计算中通常引入偏载系数来简化受力分析。从桥梁荷载试验的角度,对于拼装式结构,横向分布系数和平面有限元程序的结合能有效满足试验要求,而在宽幅连续梁桥的荷载试验中,由于要对每个测点的挠度和应变值进行准确计算,偏载增大系数和平面有限元程序往往难以满足其对试验数据的分析要求,通常需要进行实体有限元计算。
陈国强提出了用实体有限元计算宽箱梁偏载系数的方法,并将有限元计算的偏载系数与简化计算结果进行了对比;苏俭等利用实体有限元模型对变截面连续梁桥偏载系数沿跨度的分布规律进行了分析,指出不同位置的截面应取不同的偏载系数;薛兴伟等使用实体有限元对支座脱空等边界条件变化对偏载系数的影响进行了分析。以上研究均是从理论计算的角度对桥梁的偏载系数进行分析,缺乏实测数据对研究结论的验证。该文结合某等高度连续梁桥的偏载试验,验证利用实体有限元方法计算偏载系数的准确性。
1 偏载系数的简化计算方法
箱梁在偏心的作用下将产生纵向弯曲、扭转、横向挠曲和畸变变形,其中偏心活载引起的扭转及扭曲正应力比活载引起的弯曲正应力小得多,同时箱形截面的横向刚度和扭转刚度都很大,在偏心活载作用下,截面的竖向位移也是主要的。因此,在箱梁设计时,通常引入偏载系数对初等梁理论进行修正,按照纵、横向两个方向分别计算。但中国现行规范尚未对偏载系数的计算作详细规定,也未形成成熟统一的理论计算公式。常用的偏载系数计算方法有经验系数法、偏心压力法和修正的偏心压力法。
(1)经验系数法。在箱壁较厚且有横隔板的情况下,截面因畸变引起的扭曲应力可忽略不计,而活载偏心作用引起的约束扭转正应力一般只为活载对称作用引起的弯曲正应力的15%。因此,在计算箱梁截面某点的正应力时可忽略箱梁的畸变效应,只考虑箱梁的纵向挠曲及约束扭转效应,在各肋板平均承受外荷载的基础上,把边肋上所受的荷载增大15%,即偏载系数ξ=1.15。经验系数法最简单,但过于笼统,它既不考虑结构尺寸,也不考虑荷载和偏心的大小,因而通常会给出不安全的结果。
(2)偏心压力法。偏心压力法是桥梁荷载横向分布计算的一种常用方法,它假定横隔梁刚性极大,也称为刚性横梁法。偏心压力法最初用来计算开口截面T形梁桥的荷载横向分布系数,将其用于求解连续砼箱梁的偏载系数,是其应用的一个推广。该理论将箱梁的腹板看作是开口截面的梁肋,计算出边肋的横向分配系数,然后乘以总的梁肋数,即可求得偏载系数,计算公式见式(1)、式(2)。偏心压力法忽略了主梁的抗扭刚度而假定横向刚度无限大,当桥宽较大时横梁相对刚度降低,计算结果会带来较大误差,同时考虑桥梁跨度对偏载系数的影响。

式中:n为箱梁的肋板数;e为外荷载合力点至桥面中心的距离;y1为边肋至桥面中心的距离;yi为各肋板至桥面中心的距离。
(3)修正的偏心压力法。偏心压力法假定横梁刚度无限大,没有考虑箱梁抗扭刚度这一重要因素。修正的偏心压力法在偏心压力法的基础上,为考虑箱梁的扭转刚度,引入抗扭刚度修正系数β,计算公式见式(3)~(5)。修正的偏心压力法虽然考虑了主梁的抗扭刚度,但它是从计算拼装肋梁式桥梁出发的,在扭转作用下,闭口箱形截面与拼装肋梁式开口截面的剪力流有着本质的区别,单箱多室桥梁梁肋数量越多,偏差也越大。
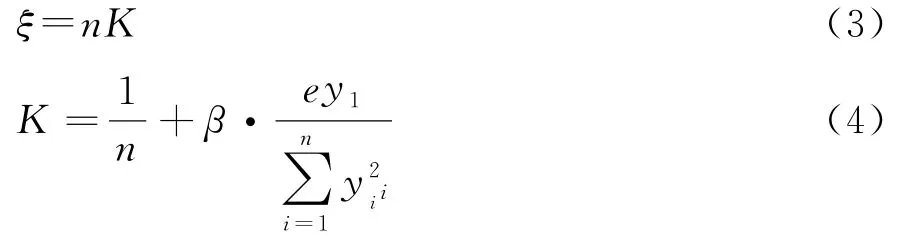

式中:l为连续箱梁中被考察的某跨的长度;G、E分别为箱梁材料的抗剪、抗弯弹性模量;I、IT分别为箱梁截面的抗弯、抗扭惯性矩。
2 工程实例
2.1 工程概况
荷载试验桥梁的上部结构为3×35 m预应力砼连续箱梁、等高度斜腹板箱梁结构。主梁采用单箱四室截面,按照A类预应力结构设计。单幅桥面宽22 m,边室净宽3.625 m,中室净宽3.65 m,悬臂2.3 m。腹板厚度0.45~0.7 m,底板0.25~0.45 m,顶板0.25 m,悬臂端部0.20 m,根部0.45 m。每跨支点处设置横梁,中支点横梁宽度为2.5 m,端支点横梁宽度1.5 m。桥面布置为5.0 m人行道+ 16.5 m机动车道+0.5 m中央分隔带。设计荷载为公路-Ⅰ级。
2.2 箱梁的有限元分析
采用ANSYS对箱梁进行静力学分析。分析计算时,砼弹性模量E取3.45×104MPa,砼容重取25 k N/m3,泊松比取0.166 7。箱梁采用Solid45单元模拟。对该桥进行结构静力分析时,根据支座位置设置边界条件。箱梁有限元模型见图1。箱梁中的预应力对称作用于结构上,与偏心活载无关,故建模时未考虑预应力的作用。

图1 箱梁有限元模型
2.3 偏载试验
为了验证箱梁实测偏载系数和计算值的偏差,对该桥进行偏载试验。桥梁为单向行驶,根据设计规范,偏载试验采用四车道布载,以边跨15 m断面和中跨跨中断面为试验控制断面。荷载效率见表1,测试断面布置见图2。
经理论计算,偏载试验共使用8辆重约30 t的三轴载重车辆加载,前轴重约6 t,双后轴重约24 t,使荷载效率满足JTG/T J21-2011《公路桥梁承载能力检测评定规程》的要求(0.95~1.05)。每个控制断面均布置5个挠度、5个应变测点,挠度和应变测点均布置在腹板中心下方的梁底面(见图3)。应变测试采用电阻应变片,挠度测量采用电测位移计。加载车辆的横向、纵向布置见图4~6。

表1 偏载试验荷载效率


图3 挠度和应变测点布置(单位:cm)

图4 车辆荷载的横向布置(单位:cm)

图5 中跨偏载工况车辆纵向布置(单位:cm)

图6 边跨偏载工况车辆纵向布置(单位:cm)
2.4 偏载试验结果
在进行静力学计算时,将车辆荷载的轮载等效成集中力,作用于相应节点上。中跨和边跨在偏载车辆作用下,控制断面处等弯矩区单元的竖向位移和纵向应力云图见图7~10。

图7 A断面处的竖向位移云图(单位:mm)

图8 A断面处的纵向应力云图(单位:MPa)

图9 B断面处的竖向位移云图(单位:mm)
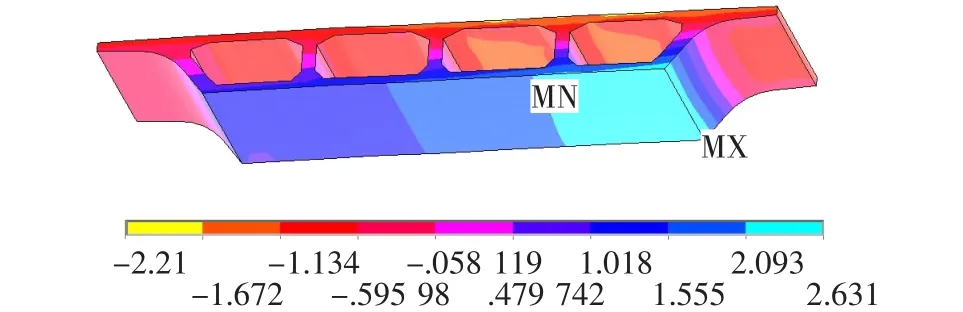
图10 B断面处的纵向应力云图(单位:MPa)
从图7~10可以看出:在控制断面处的等弯矩区,挠度最大值出现在偏载侧的外侧翼缘板的边缘,最大拉应变出现在偏载侧梁底的外侧边缘;主梁控制断面处应力、挠度变化趋势基本一致,均由偏载一侧向另一侧逐渐减小。
主梁控制断面在偏载作用下的实测和计算挠度见表2,实测和计算应变表3。

表2 中跨、边跨偏载工况实测和理论挠度 mm

表3 中跨、边跨偏载工况实测和理论应变 με
3 偏载系数对比
表4为实测挠度和应变偏载系数、有限法和简化计算公式所得偏载系数。从中可以看出:
(1)对比简化计算方法得到的偏载系数与实测值,经验系数法得到的偏载系数为1.15,远小于实测值,在进行验算分析时,取用该经验系数偏于不安全;偏心压力法计算得到的偏载系数最大,远大于实测偏载系数,若用于桥梁设计计算,会造成资源的严重浪费;而考虑箱梁抗扭修正后得到的偏载系数小于实测偏载系数,若采用修正偏心压力法计算得到的偏载系数,对桥梁结构也偏于不安全。
(2)对于中跨和边跨的偏载系数,简化计算结果未能反映中跨和边跨偏载系数的区别,而实测和有限元计算结果均表明边跨的偏载系数略大于中跨。同时有限元方法计算得到的偏载系数与实测值十分接近,最大偏差仅为5.1%,使结构既能满足安全性需要,又最为经济合理。

表4 偏载系数实测和计算结果
4 结论
该文通过工程实例,对等高度连续箱梁的偏载系数进行实测和计算分析,结论如下:传统的简化计算方法与实测值存在较大偏差,其中经验系数已不能满足工程安全的需要;偏心压力和修正的偏心压力法均未考虑桥墩的结构形式,其计算值也与实测值有较大偏差。实体有限元法计算结果与实测结果相吻合,该方法既能反映主梁本身的横向刚度,又能有效模拟支座和桥墩类型对偏载系数的影响,实用性最强,结果也最为可靠,建议优先采用。
参考文献:
[1]陈国强.连续宽箱梁的偏载增大系数的讨论[J].公路交通科技,2013,30(7).
[2]苏俭,刘钊,阮静.连续梁桥的活载正应力偏载系数研究[J].世界桥梁,2009(4).
[3]薛兴伟,袁鸿达.连续箱梁桥偏载系数三维有限元分析及工程应用[J].城市道桥与防洪,2011(1).
[4]程翔云.梁桥理论与计算[M].北京:人民交通出版社,1990.
[5]程翔云,尚春青.对箱形截面连续梁活载内力增大系数的评述[J].公路,2000(1).
[6]王勇,刘永健,唐小方.混凝土连续箱梁偏载系数简化算法研究[J].长沙交通学院学报,2006,22(3).
[7]郭忆,叶见曙,万红燕.预应力混凝土箱梁偏载系数试验研究[J].黑龙江工程学院学报,2002,16(4).
收稿日期:2015-10-22
中图分类号:U441
文献标志码:A
文章编号:1671-2668(2016)02-0158-04
