基于梁-索-阻尼器耦合振动的阻尼器减振效果数值分析∗

刘大洋,胡建新,廖敬波,刘波

(招商局重庆交通科研设计院有限公司,重庆 400067)



基于梁-索-阻尼器耦合振动的阻尼器减振效果数值分析∗

刘大洋,胡建新,廖敬波,刘波

(招商局重庆交通科研设计院有限公司,重庆 400067)

摘要:以厦漳跨海大桥2根安装外置阻尼器的不同参数的斜拉索为工程背景,通过数值方法分析在梁-索-阻尼器耦合振动下外置阻尼器对拉索位移、速度、加速度的减振效果。结果表明,较短的S05拉索,外置阻尼器对拉索振动的位移、速度、加速度的减振幅度为41.32%～66.55%,减振效果均很明显;较长的N18拉索,外置阻尼器对拉索振动的位移、速度、加速度的减振幅度分别为12.53%～59.04%、20.92%～60.18%、40.58%～62.07%,长索各采集点的3个参数的减振幅值随采集点向L/2索长高度延伸均有不同程度的减小,3个参数减振幅值减小趋势由大到小依次为位移参数、速度参数、加速度参数。

关键词:桥梁;耦合振动;外置阻尼器;减振效果;数值分析

近几十年,随着高强材料、设计理论、计算机工具的快速发展及施工工艺与管理水平的不断提高,景观优美、跨越能力强的斜拉桥得到突飞猛进的发展。随着跨径的不断增大,斜拉索的大幅振动问题越发严重。拉索的振动,使拉索锚固端、拉索与锚具的结合处出现疲劳裂纹,索中平行钢丝产生相对滑动而使PE等保护材料发生破坏,钢丝出现锈蚀,威胁整个桥梁的安全。

在工程应用中,为抑制拉索的大幅振动,在桥面与拉索之间安装外置剪切型粘滞阻尼器成为常用的减振手段之一,该阻尼器可提供较大的阻尼力,且具有减振效果明显、价格低廉、可靠性高、鲁棒性好等特点。拉索安装外置阻尼器后,拉索的振动模型变为梁-索-阻尼器的耦合振动,而目前关于耦合振动下外置阻尼器对拉索减振效果的相关研究较少。该文以厦漳跨海大桥2根分别代表不同长度、弯曲刚度、索力、外置阻尼器等参数的拉索为工程背景,通过有限元软件建立单根拉索的梁-索-阻尼器模型,引入拉索与阻尼器端部实际存在的外界环境激励,分析该激励下外置阻尼器对拉索的减振效果。

1 梁-索-阻尼器耦合振动介绍

随着有限元计算方法的不断发展,以前很复杂的耦合振动问题成为研究热点。该文针对安装外置阻尼器减振设备的长短斜拉索,通过在有限元分析模型中施加白噪声激励来模拟现场的环境激励。常见梁-索-阻尼器耦合振动模型有:1)不考虑桥面对拉索端部的外界时程激励;2)只考虑桥面对拉索端部的外界时程激励;3)只考虑桥面对阻尼器安装端部的外界时程激励;4)同时考虑桥面对拉索端部和阻尼器安装端部的外界时程激励(见图1)。

图1(a)最为简化,即在现场不考虑拉索端部和阻尼器端部的环境激励,这也是目前在工程中经常采用的简化方法。但在实际桥梁中,桥面的环境激励是不可避免的,尤其是大跨度斜拉桥。图1(b)只在拉索端部施加时程激励,模拟主梁-拉索的耦合振动。图1(c)只在阻尼器端部施加时程激励,由于在桥上阻尼器的安装位置距拉索的桥面锚固端较近,拉索端部和阻尼器安装端部的桥面振动相差较小。该文研究中不单独考虑这种情况,而是直接按图1(d)考虑,在拉索端部和阻尼器安装端部同时施加x、y方向的位移时程激励。

2 梁-索-阻尼器耦合振动建模

2.1 拉索基本参数

选取厦漳跨海大桥南汊主桥一根相对短索和北汊主桥一根相对长索为研究对象,拉索编号分别为S05与N18,其基本参数见表1。

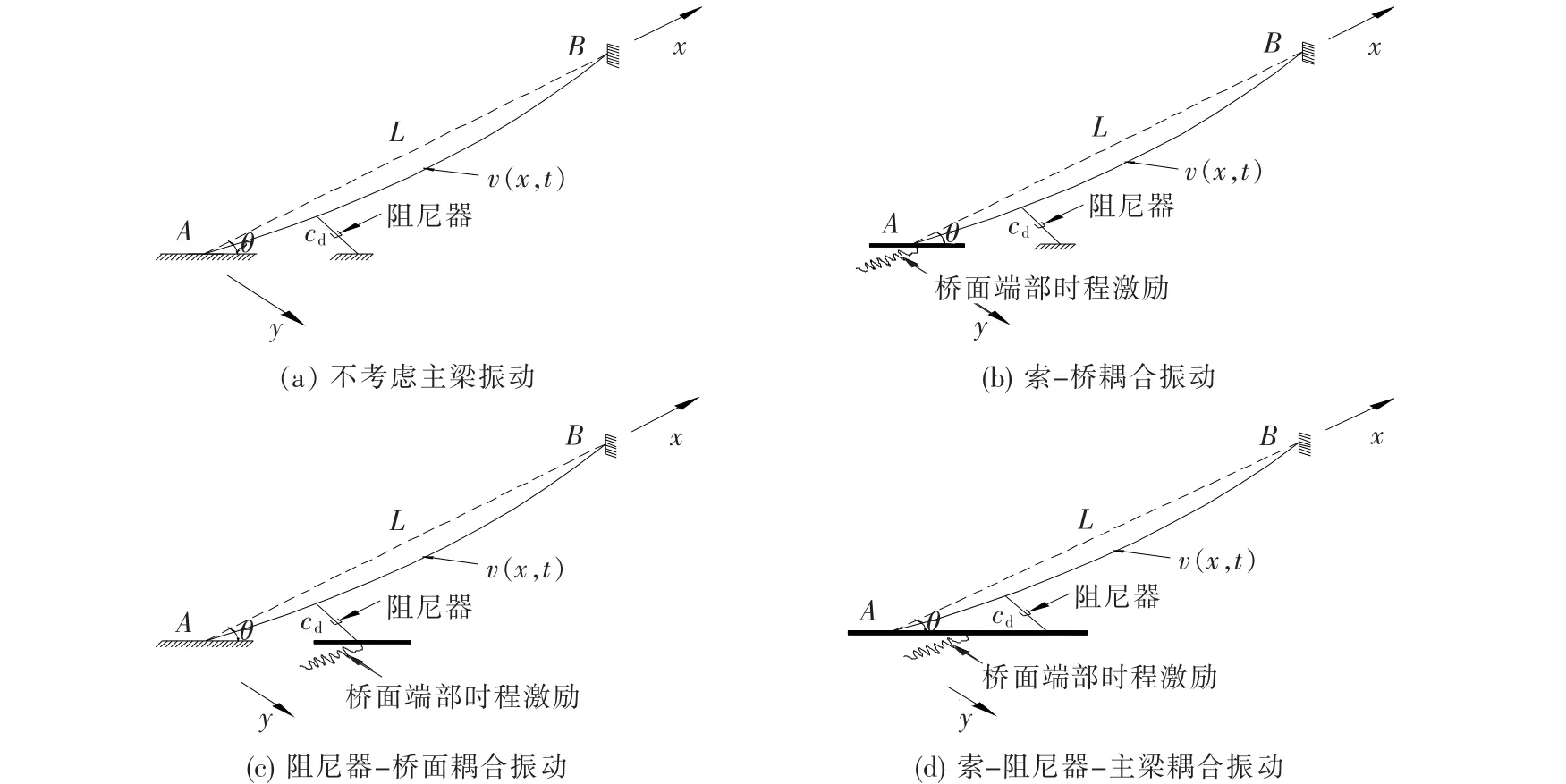
图1 常见梁-索-阻尼器耦合振动模型

表1 拉索的技术参数

拉索的桥面激励在模型中用高斯白噪声模拟。高斯白噪声幅值服从高斯分布,功率谱密度服从均匀分布,可较好地模拟桥面的环境激励。模拟桥面激励的高斯白噪声位移时程见图2。

图2 桥面激励的高斯白噪声位移时程曲线

2.2 拉索模型建立

采用有限元软件ANSYS建立梁-索-阻尼器的耦合振动模型,模型中的拉索采用Link10单元模拟,Link10单元具有双线性刚度矩阵特性及应力刚化、大变形功能,是轴向仅受拉或仅受压杆单元。阻尼器系统采用Combin14单元模拟,Combin14是一个弹簧-阻尼器系统单元,具有弹簧常数K与阻尼系数C两个实常数。

建立拉索模型,对拉索的两端和阻尼器端部节点施加全约束,按倾角方向施加重力加速度模拟拉索斜度。先对系统进行静力分析、模态分析,得出拉索的自振频率;再对系统进行瞬态分析,按上述工况分别在拉索桥面端部输入位移时程、拉索和阻尼器端部同时输入位移时程,提取拉索不同位置的位移、速度、加速度时程曲线。2根拉索的信号采集点见图3。

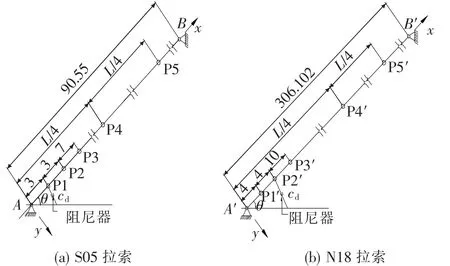
图3 拉索采集点示意图(单位:m)

数据采集点的布置首先考虑阻尼器的位置,短索的第一个测点布置在阻尼器位置,剩余测点依次向拉索中间布置至L/2;长索的第一个测点布置在桥面与阻尼器之间,第二个测点布置在阻尼器位置,剩余测点依次向拉索中间布置至L/2。

在有限元模型中分别采集以上各测点在白噪声激励下的位移、速度和加速度时程曲线。

3 梁-索-阻尼器耦合振动数据分析处理

3.1 信号降噪处理

在模型中施加模拟环境激励的位移白噪声时,采集的数据信号会受到很多高频信号的干扰,以sym7小波基为降噪小波基,对采集的位移、速度和加速度信号进行降噪处理,通过降噪后与降噪前信号的信噪比和均方根误差来判断降噪效果。以S05号拉索在拉索与阻尼器端部同时输入位移时程工况下P4点的速度信号为例,降噪效果见图4。

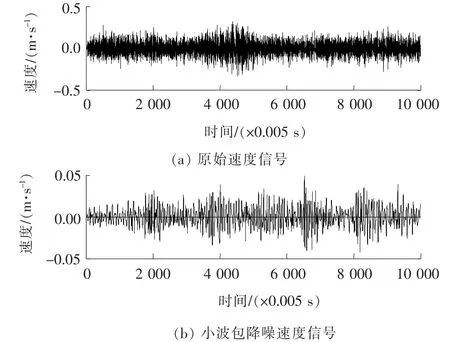
通过对P4点位移、速度和加速度信号的降噪效果对比,发现P4点3种信号的降噪效果中,速度的降噪效果最好,位移的降噪效果次之,加速度的降噪效果较差。

3.2 阻尼器的减振效果

通过采集安装外置阻尼器前后2根拉索的位移、速度和加速度信号并进行分析,对比外置阻尼器对长、短拉索的减振效果。

3.2.1 短索的减振效果

南汊主桥S05号拉索的P1点位于阻尼器位置[见图3(a)],距桥面较近,本身的振幅很小,加之在阻尼器端部施加有位移时程激励。因此,该点的减振效果不作对比。以拉索L/2点为例,绘图说明在安装外置阻尼器前后位移、速度和加速度时程的减振效果(见图5)。其余P2、P3、P4点的外置阻尼器的减振效果不单独列图,直接用表格对比减振作用(见表2)。

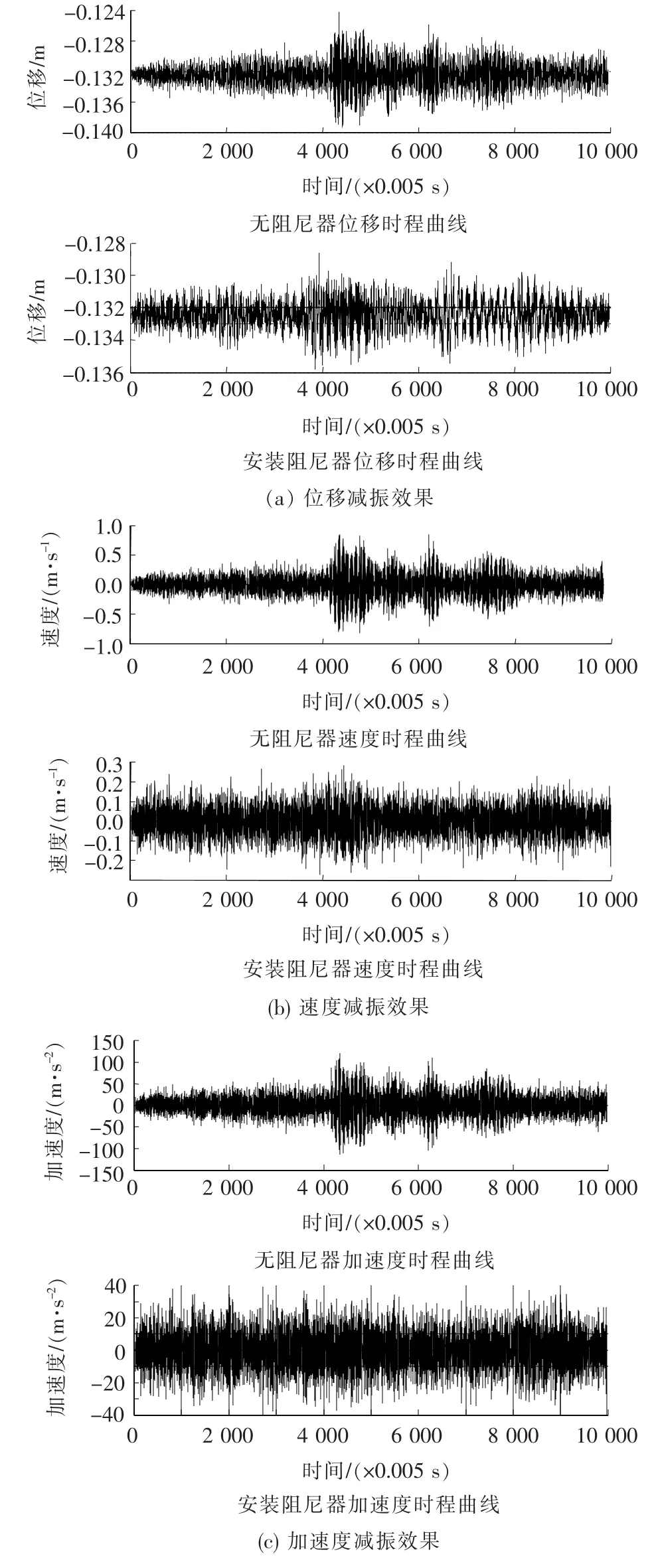
图5 S05号拉索L/2点的减振效果对比

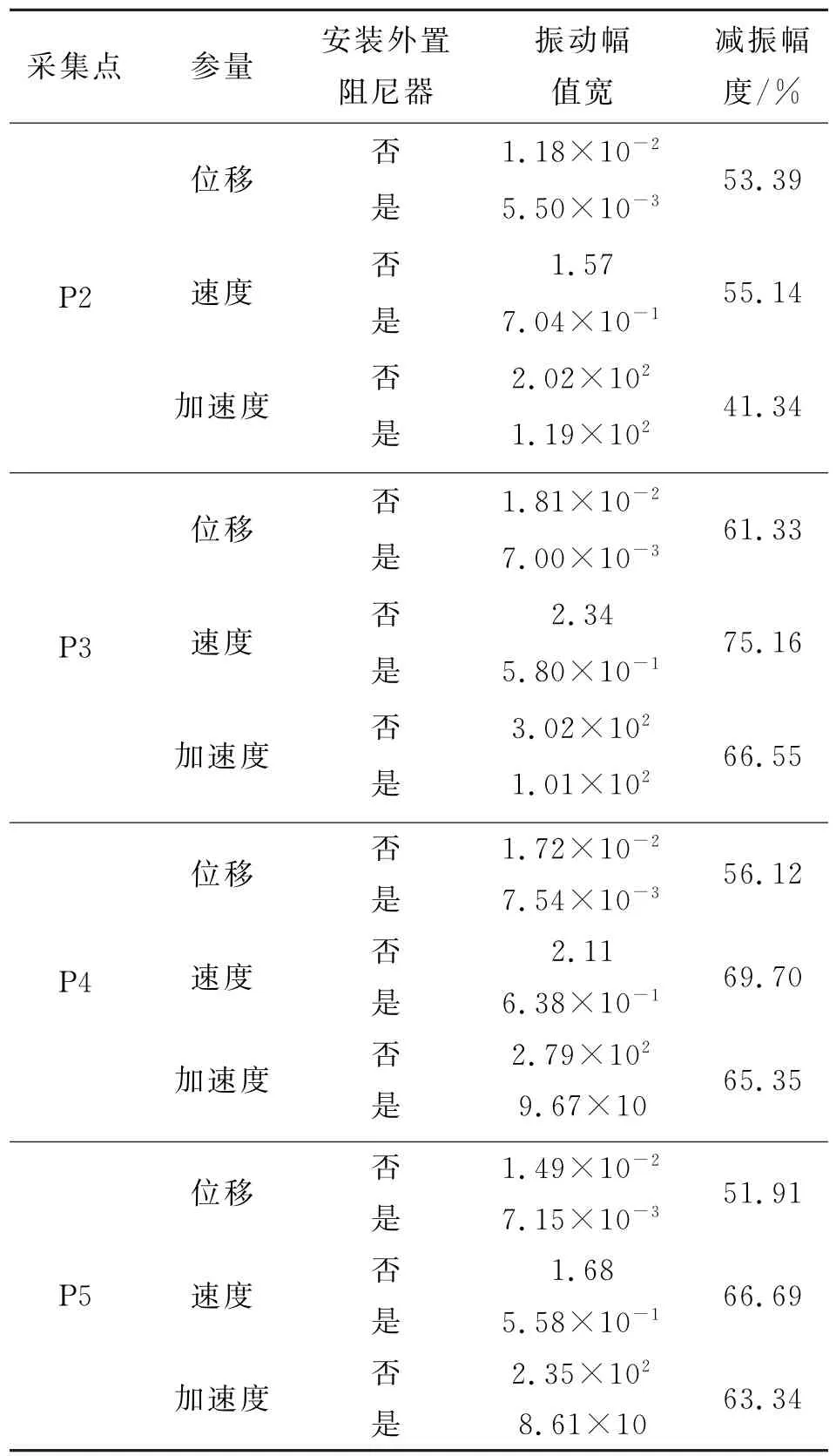
表2 短索外置阻尼器减振效果对比

由图5可看出:安装外置阻尼器后,位移、速度和加速度的减振效果均很明显。

由表2可看出:S05号拉索在安装外置阻尼器后,3个数据采集点的位移减振幅值为51.91%～61.33%,速度减振幅值为55.14%～75.16%,加速度减振幅值为41.32%～66.55%,减振效果均很明显。短索各采集点的3个参数的减振幅值随采集点向L/2索长高度延伸无明显变化。

3.2.2 长索的减振效果

北汊主桥的N18号拉索的第一个采集点P1′位于外置阻尼器与桥面的中点位置[见图3(b)],此处振幅较小,且受拉索端部和阻尼器端部的位移时程激励的影响。第二个采集点P2′位于阻尼器位置,受阻尼器端部施加的位移时程激励的影响。因此,不对P1′、P2′点的采集信号作减振效果对比。P3′、P4′、P5′点的外置阻尼器位移、速度和加速度的减振效果见表3。

表3 长索外置阻尼器减振效果对比

由表3可看出:N18号拉索在安装外置阻尼器后,3个数据采集点的位移减振幅值为12.53%～59.04%,速度减振幅值为20.92%～60.18%,加速度减振幅值为40.58%～62.07%。相对于短索,长索各采集点的3个参数的减振幅值随采集点向L/2索长高度延伸均有不同程度的减小,其中位移减振幅值减小趋势最明显,速度减振幅值减小趋势次之,加速度减振幅值减小趋势最小。

4 结论

该文通过有限元软件模拟单根拉索的梁-索-阻尼器耦合振动,按照斜拉索阻尼器的实际位置参数与阻尼器参数,引入拉索与阻尼器端部实际存在的外界环境激励,分析该种激励下外置阻尼器对拉索的减振作用,主要结论如下:

(1)对于较短的S05拉索,在安装外置阻尼器后,3个数据采集点的位移减振幅值为51.91%～61.33%,速度减振幅值为55.14%～75.16%,加速度减振幅值为41.32%～66.55%,减振效果明显。

(2)对于较长的N18拉索,在安装外置阻尼器后,3个数据采集点的位移减振幅值为12.53%～59.04%,速度减振幅值为20.92%～60.18%,加速度减振幅值为40.58%～62.07%。相对于短索,长索各采集点的3个参数的减振幅值随采集点向L/2索长高度延伸均有不同程度的减小,其中位移减振幅值减小趋势最明显,其次为速度减振幅值减小趋势,加速度减振幅值减小趋势最小。

参考文献:

[1]Sena Kumarasena,Nicholas P Jones,Peter Irwin,et al.Wind induced vibration of stay cables[R].Federal Highway Administration,2005.

[2]项海帆.现代桥梁抗风理论与实践[M].北京:人民交通出版社,2005.

[3]王修勇,陈政清,倪一清.斜拉桥拉索风雨振观测及其控制[J].土木工程学报,2003,36(6).

[4]郭亚.振动信号处理中的小波基选择研究[D].合肥:合肥理工大学,2003.

[5]梁栋,陈培,李岩峰.索梁耦合振动对拉索阻尼器的影响机理[J].振动、测试与诊断,2014,34(1).

收稿日期:2015-11-10

基金项目:∗重庆市科技人才计划项目(cstc2014kjrc-qnrc30003)

中图分类号:U441

文献标志码:A

文章编号:1671-2668(2016)02-0154-04