公路软基处理方案技术决策的Bayes判别分析法
2016-04-20刘三豆
刘三豆
(湖南路桥建设集团有限责任公司,湖南长沙 410004)
公路软基处理方案技术决策的Bayes判别分析法
刘三豆
(湖南路桥建设集团有限责任公司,湖南长沙 410004)
摘要:将Bayes判别分析法应用于软基处理方案决策中,建立了软基处理方案技术决策的Bayes判别分析模型;选用软土层厚度、软土压缩模量、地表硬层厚度和路堤填土高度等4个属性参数作为确定软基处理方案的判别因子,将软基处理技术方案分为不处理、浅层处理和深层处理等3个层次并作为Bayes判别分析的3个正态总体,以15个软基工程实测数据作为训练样本,建立Bayes线性判别函数;以Bayes线性判别函数计算待判样品的Bayes判别函数值,以Bayes判别函数值的最大值对应的总体作为待判样品所归属的总体;最后以回代法对判别准则进行评价,结果表明Bayes判别分析模型回判估计误判率低,且13个判别结果与实际工程中采用的处理方法基本一致,模型的应用效果优良。
关键词:公路;Bayes判别分析法;软基处理;方案决策
在软土地基上进行路基工程建设,首先需要对地基是否处理及是采用浅层处理还是深层处理方法等作出技术决策。目前,软基浅层处理和深层处理方法很多,主要有置换法、排水固结法、贯入固化物、振密、挤密、加筋、超载预压和搅拌桩等,每种方法有其优点,也存在适用范围和一定的局限性。此外,由于地基处理设计理论不完善且不确定性因素多,进行技术方案决策难度大,工程师的经验在地基处理方案技术决策中往往起着重要作用,但对缺少工程经验的工程技术人员来说可能有盲目性,因而如何使软基处理技术决策更具科学性非常重要。
冯仲仁等认为地质、工程、经济和环境等因素影响软基处理技术决策,而这些因素带有随机性和未知性,据此基于范例推理、模糊数学提出了高速公路软基处理方案决策模型;高景伟等基于模糊数学理论,提出了模糊相似优先的软基方案优选方法;张留俊等认为在公路软基处理方案决策中需考虑定量和非定量等因素的影响,并基于模糊数学和层次分析法建立了多层次模糊综合评判模型,以解决公路软基处理方案的优选问题;冯仲仁等提出灰色关联度、神经网络等公路软基处理方案决策模型;陈向阳等将自适应共振与神经网络相结合对软基处理方案进行决策;罗君君等基于模糊数学和物元分析理论,引入语言变量和熵权对公路软基处理方案优选进行决策;张士励等基于误差理论和区间数理论,将误差传递公式和可能度公式相结合,对软基处理方案优选进行决策;彭小云等基于实例类比推理的智能方法,对高速公路软基处理方案进行决策;刘勇等基于模糊理论和层次分析法,对吹填土路基处理方案进行决策。这些决策模型和方法从不同侧面反映了影响软基处理方案决策的不确定因素。但对于软基处理技术决策这类复杂问题的求解需多种方法和途径的互补才能达到预期目的。基于这一考虑,该文提出一种基于Bayes判别分析法的软基处理技术决策模型和方法,为工程实践提供新的途径和方法。
1 Bayes判别方法
1.1 Bayes判别方法的基本思想
用统计的语言来描述,Bayes判别分析方法就是:已知g个p维总体G1,G2,…,Gg,每个总体Gi可认为是属于Gi的指标X=(X1,X2,…,Xp)T取值的全体,它们分别具有互不相同的p维概率密度函数f1(x),f2(x),…,fg(x)。在进行判别分析之前,对所研究的总体在抽样前已有一定的了解,常用先验概率分布来描述这种认识,然后基于抽取的样本对先验认识作修正,得到后验概率分布以进行统计推断。在实际应用中,判别分析需提取训练样本中各总体的信息以构造一定的准则来决定新样品的归属问题。将Bayes统计思想用于判别分析就得到Bayes判别方法。
1.2 多正态总体的Bayes判别
设g个p维正态总体G1,G2,…,Gg,其概率密度函数为:

式中:i=1,2,…,g;μ为数学期望;∑为协方差矩阵。
假设各正态总体的协方差矩阵相等,即∑1= ∑2=…=∑g=∑,则得到判别函数为:

式中:qi为总体的先验概率分布。
实际应用中,若μi、∑i未知,则以训练样本作估计,即以训练样本的样本均值(i)和样本方差Si作为μi和∑i的估计,此时有:

1.3 判别准则


1.4 判别准则的评价


式中:n(1)1为属于G1的样品被错判的个数;n(2)2为属于G2的样品被错判的个数;…;n(g)g为属于Gg的样品被错判的个数。
2 软基处理方案决策的Bayes模型
2.1 训练样本的准备
通过研究土的物理力学指标之间的相关关系,文献[3]选用4个参数即软土层厚度、软土压缩模量、地表硬层厚度、路堤填土高度,3种地基处理方式即不处理、浅层处理、深层处理(浅层处理有换填土、砂垫层等,深层处理有砂井预压、塑料排水板预压、粉体搅拌桩、碎石桩、二灰桩等),以15个软基处理工程实例(见表1)建立基于范例推理的软基处理决策模型,取得了较好的工程应用效果。该文同样以这15个软基处理工程实例作为研究对象,建立公路软基处理技术决策Bayes判别模型。

表1 软基工程样本
2.2 Bayes判别分析函数
由于表1中15个工程实例已研究清楚并有明确结论,将每个工程实例的属性参数及处理方式构成一个训练样本,其中属性参数包括软土层厚度、软土压缩模量、地表硬层厚度及路堤填土高度等分别设为x1、x2、x3、x4,软基处理方式包括不处理、浅层处理及深层处理分别设为G1、G2、G3,得到分别属于总体G1、G2、G3,容量分别为3、4、8的训练样本。以表1中数据建立Bayes判别准则,并对其优良性作出评价。
假定3个总体的协方差矩阵相等,按照第1节的方法建立Bayes判别函数为:

2.3 模型优良性检验
以前述判别准则对上述判别函数的优良性进行检验,即以所建立的准则对表1中训练样本的各样品进行回判。回判结果如下:误判情况只有第7号样品,即属于G2的第7号样品被误判为G1,得到回代误判率为6.67%,正确识别率为93.33%,模型判别准则的优良性较高。
2.4 判别实例
从文献[16]中选择13个软基工程(见表2)检验Bayes模型的判别结果。属性参数中,软土层厚度、软土压缩模量、地表硬层厚度及路堤填土高度等分别以x1、x2、x3、x4表示;地基处理方式中,不处理以G1表示,砂沟、砂垫层和排水带等为浅层处理(G2),排水板、粉喷桩、砂井及袋装砂井等为深层处理(G3)。将以上参数分别代入式(6),以式(4)进行判别,结果见表2。判别结果与实际工程中采用的处理方法基本一致。
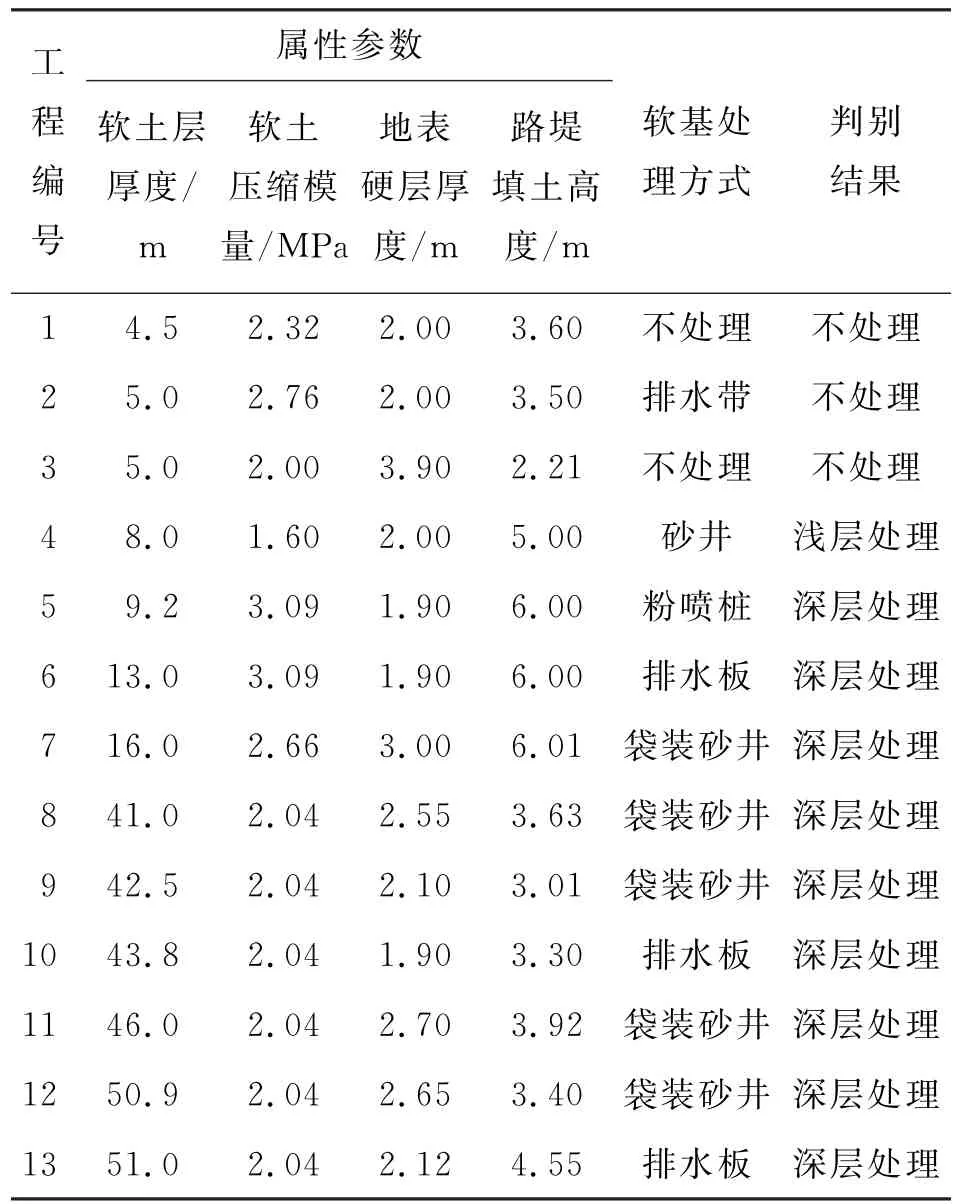
表2 Bayes模型的判别结果
3 结语
在路基工程软基处理方案技术决策中,选用3种软基处理方案即不处理、浅层处理和深层处理,综合考虑了软基处理方案在工程实际中的可操作性、广泛性和适用性。同时以软土层厚度、软土压缩模量、地表硬层厚度和路堤填土高度等4个属性参数作为决策因子,既考虑了地质因素(软土压缩模量和地表硬层厚度),又考虑了工程因素(软土层厚度和路堤填土高度),并考虑了这些指标的相关关系,即土的物理力学指标之间的相关关系。
以Bayes判别分析方法建立软基处理方案技术决策数学模型,通过对判别准则优良性的检验,得到了较为满意的结果,为软基处理方案技术决策提供了数量化和定量化的途径。
由于训练样本容量的限制,模型的代表性和准确性会受到一定影响。在今后的研究中,应广泛收集软基工程实例资料,增大训练样本的容量,提高其代表性和准确性,从而增强该模型的工程适应性。
参考文献:
[1]龚晓南.地基处理[M].北京:中国建筑工业出版社,2005.
[2]吴昌胜,朱志铎.沪苏浙高速公路软基处理评价[J].岩土工程学报,2015,37(增刊1).
[3]冯仲仁,陈向阳,鄢恒珍.基于范例推理的公路软基处理方案决策模型[J].岩土力学,2004,25(11).
[4]冯仲仁,朱瑞赓,姚爱民.高速公路软基处理方案的多层次模糊决策[J].岩石力学与工程学报,2002,21(6).
[5]张留俊,黄晓明,尹利华.公路软基处理方案多层次模糊综合评价方法研究[J].公路交通科技,2007,24(3).
[6]高景伟,姬怀卿,董秀坤.陕蒙高速公路软基处理方案优选方法[J].公路交通科技,2006,23(12).
[7]冯仲仁,陈向阳,鄢恒珍.基于灰色理论的软基处理方案决策模型[J].武汉理工大学学报,2004,26(10).
[8]冯仲仁,汪爱兵.5参数高速公路软基处理方案ANN决策模型[J].岩土力学,2004,25(9).
[9]陈向阳,夏元友,鄢恒珍.基于ART网络的高速公路软基处理决策模型[J].武汉理工大学学报,2007,29(2).
[10]罗君君,郑俊杰,孙玲.基于语言变量和熵权的公路软基处理方案模糊物元决策分析法[J].公路交通科技,2009,26(5).
[11]张士励,张亦飞,袁航新,等.考虑指标不确定性的软基处理方案优选模型[J].铁道工程学报,2010(3).
[12]彭小云,张志宏,毕选生,等.基于实例类比推理的软基处理方案决策方法[J].中外公路,2008,28(1).
[13]刘勇,祝艳波,余宏明,等.多层次模糊综合决策优选软基处理方案[J].地质科技情报,2011,30(3).
[14]梅长林,周家良.实用统计方法[M].北京:科学出版社,2002.
[15]张尧庭,方开泰.多元统计分析引论[M].北京:科学出版社,2003.
[16]冯仲仁.高速公路软基处理智能决策支持技术研究[D].武汉:武汉理工大学,2003.
收稿日期:2015-11-10
中图分类号:U416.1
文献标志码:A
文章编号:1671-2668(2016)02-0116-03
