基于多项式的拟合推估法在GPS高程转换中的应用
2016-04-20刘玮石杏喜
刘玮,石杏喜
(南京理工大学土木工程系,江苏南京 210094)
基于多项式的拟合推估法在GPS高程转换中的应用
刘玮,石杏喜
(南京理工大学土木工程系,江苏南京 210094)
摘要:对于GPS道路高程转换问题,常采用多项式拟合、神经网络和平均加权法进行拟合,这些方法都存在一些模型上的缺陷,造成精度降低。文中采用基于多项式的拟合推估法进行GPS道路高程转换,并通过工程实例对几种转换方法进行比较分析,证明拟合推估法比单一转换模型具有更高的精度和可靠性。
关键词:公路;高程转换;多项式拟合推估;高程异常
拟合推估法即最小二乘配置法,是根据最小二乘原理,集合经典测量平差、滤波、推估于一身,根据特定的拟合法则,对随机参数和非随机参数进行推估,使其精度更高的一种处理方法。常规的平面拟合、曲面拟合、多面函数拟合等都是拟合一个与大地水准面相似的趋势面,没有考虑趋势面与大地水准面之间的差值,也就是将全部待定参数看作非随机变量;平均加权拟合法是将高程异常值与站点平面坐标建立函数关系,对地形起伏所引起的噪声信号进行拟合,也就是将待定参数看作随机变量。无论是只考虑非随机变量还是只考虑随机变量,在理论上都是不全面的,实践中的应用也有局限。
1 多项式拟合法原理
多项式拟合法方程为:
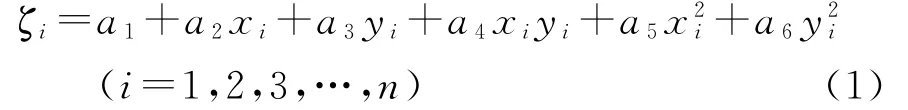
式中:x、y分别为点的纵、横坐标;a1,a2,…,a6为拟合系数。
式(1)中a1,a2,…,a6是6个待定系数,需要知道至少6个控制点才能计算出高程异常。如果式(1)中只有a1,a2,a3前三项,即为平面拟合。拟合系数可以由测区里已知点的高程异常,通过最小二乘原理求得。
误差方程为:

则矩阵形式为:

根据最小二乘原理可求得:

2 最小二乘配置法的原理
最小二乘配置的一般函数模型为:

式中:L为观测向量;X为滤波参数,即随机参数;Y为倾向参数,即非随机参数;Δ为观测噪声,Δ~N(0,DΔ)。
设观测点推估信号为X′,则式(5)可以写成:

式中:C=[B,0];Z=[X,X′]T。
已知先验信息E(X)=μX,var(X)=DX,E(X′)=μX′,var(X′)=DX′,X与X′的协方差为DXX′=DX′X,噪声Δ与X、X′的协方差是相互独立的,即DΔX′=0,DΔX=0。则误差方程为:
近日,赣州恩菲环保能源有限公司渗沥液处理站传来喜讯:项目自8月调试完毕后,已成功满负荷运行,实现成功投运,这标志着中国恩菲自主研发的渗沥液处理技术取得了重大进展,也将促进公司能源环境版块的技术提升,为公司固废领域的咨询设计、工程总包市场开拓提供新的增长点。

根据最小二乘原理:

式中:V为观测值L的改正数;VZ为Z的先验期望E(Z)的改正数。
从而得:

设B=I(单位阵)、μX=0、μX′=0,且不考虑噪声误差,则式(9)可表示为:

得到未测点的平差值为:

3 协方差函数
运用最小二乘配置模型计算异常值的过程中要预先知道各信号间的协方差,这是其成败的关键所在。实际应用中需知道各测站高程异常这一信号之间的协方差等。协方差阵往往通过协方差函数计算得到。假定协方差只与i、j两点间的距离有关,而与点间的点位和方向无关,这就是随机函数。协方差函数的确定与选择将直接影响估计值的精度。
协方差函数的严密表达式难以准确获得,实际中通常采用经验协方差函数根据观测得到的数据对其进行估计,即预先选择一个符合协方差函数条件、形式简单的函数作为协方差函数,根据观测值采用拟合方法求得所选协方差函数中的待定参数。
确定协方差函数的方法有多项式拟合、高斯曲线函数拟合、一般指数函数拟合、多面函数拟合、希尔沃年函数拟合等。鉴于一般实测中GPS高程测量和水准测量重合点不是很多,采用多面函数拟合协方差函数比较合理。
鉴于拟合区域小且GPS高程测量与水准测量重合点不多,选取平方根函数作为协方差函数,即:

由已知点的坐标(x,y)构成协方差矩阵DX:

协方差矩阵是对称方阵,其中主对角线元素σ21,…,σ2n分别是信号X的方差,σij=σji是协方差;由已知点坐标和未知点构成协方差矩阵DX′X;求得上述协方差矩阵即可通过式(10)、式(11)求得未知点的高程异常。
4 模型精度评定
模型的符合精度是根据参与拟合的已知点的实测高程与拟合高程的差值进行计算的,已知点的拟合精度称作内符合精度,检核点的符合精度称作外符合精度。其计算公式分别为:

式中:n为已知点个数;m为检核点个数。
5 实例分析
在南京某标段市政道路上设置测量点,并布置控制网,结合GPS测量及二等精密水准测量分别对各点进行试验研究。为了获得更好的试验结果,控制点尽量均匀分布,并覆盖整个控制网(见图1)。选取7个已知点(KZ1~KZ7)参与拟合,7个点(D1 ~D7)作为检核点,分别计算其拟合残差及内外符合精度。已知点、检核点的数据见表1、表2。

图1 控制网中控制点和待测点分布
本例中高程异常量值变化不大,若要达到更好的拟合精度,需将测区内全部已知点的高程异常按一定间距作等高线(见图2),从中找出已知点的最佳组合。如果个别高程异常变化量比较明显,则不适合作为拟合点和检核点。
在进行拟合计算前,先将各控制点的平面坐标减去一个常数,避免数据差异过大产生奇异矩阵,使计算更加稳定。拟合出高程异常ξ后,根据高程关系式即可求出正常高。
通过编程计算,可求得平面拟合法、平面拟合+最小二乘配置法、二次曲面和二次曲面+最小二乘配置法4种方法的拟合高程异常,并计算出拟合残差、内外符合精度,比较各种方法的优劣(见表3、表4和图3、图4)。

表1 控制点坐标和高程异常
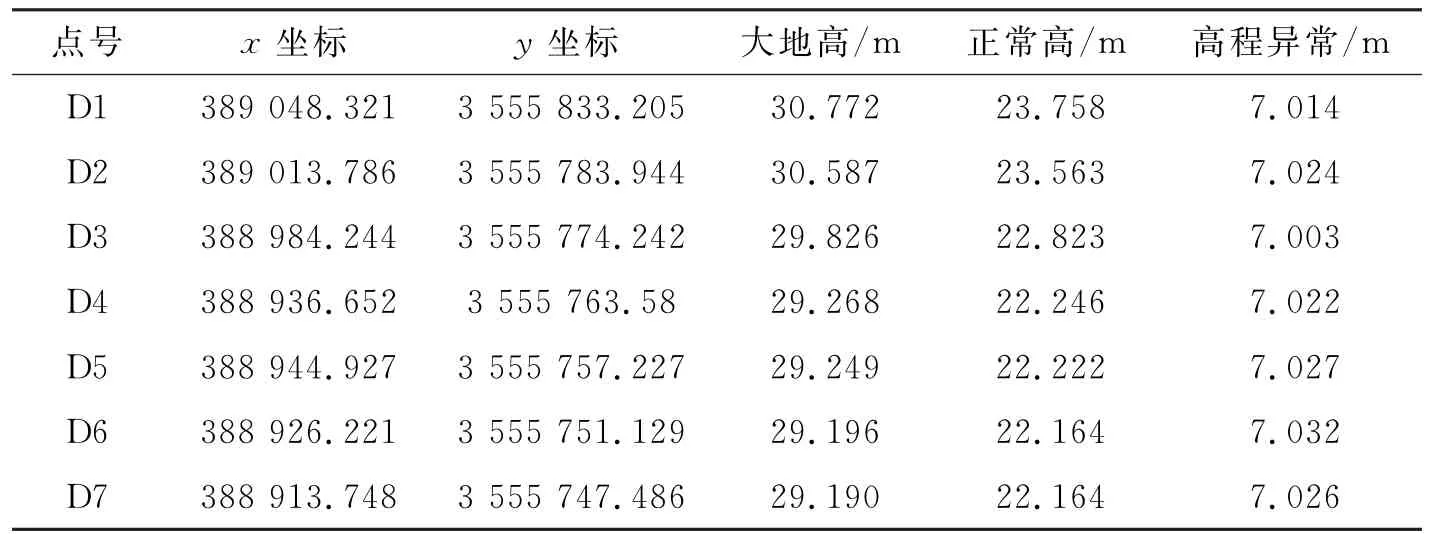
表2 待测点坐标、拟合高程和高程异常

图2 高程异常柱状图
从表3、表4和图3、图4可看出:平面拟合已知点的最大拟合残差为-1.19 cm,检核点的最大拟合残差为-1.36 cm;平面拟合+最小二乘配置法已知点的最大拟合残差为-0.9 cm,检核点的最大拟合残差为-1.10 cm;二次曲面拟合法已知点的最大拟合残差为0.6 cm,检核点的最大拟合残差为0.96 cm;二次曲面+最小二乘配置法已知点的最大拟合残差为-0.1 cm,检核点的最大拟合残差为0.9 cm。二次曲面+最小二乘配置法的内外符合精度均高于其他3种方法。

表3 已知点高程异常推估值及拟合残差

表4 检核点高程异常推估值及拟合残差

图3 已知点拟合残差
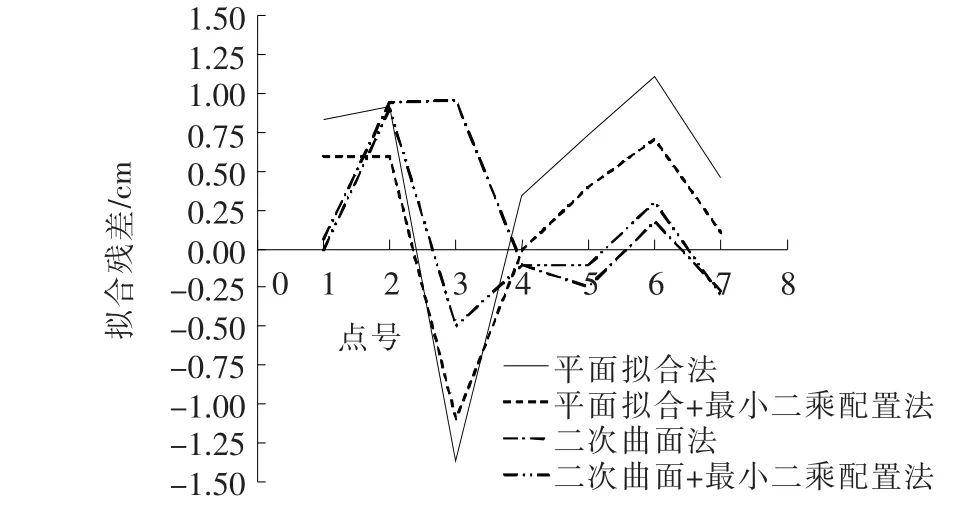
图4 检核点拟合残差
6 结论
(1)就单一模型而言,二次曲面拟合法的精度高于平面拟合法;增加最小二乘配置的多项式模型的精度高于单一模型,其精度在已知点拟合中表现更为明显。其原因是单一拟合模型易受到地形和模型的限制而影响其精度;基于多项式的拟合推估法的综合模型吸收了单一模型的优点,拟合精度高。
(2)最小二乘配置法中的协方差函数是一种统计函数,在高程异常资料稀少的地区很难确定。同时协方差函数能否正确反映信号的相关性,不仅与所选函数有关,还与参与协方差函数拟合的样本质量及容量有关。
(3)不同的协方差函数会影响拟合数据精度,鉴于一般实测中GPS高程测量和水准测量重合点不是很多,采用平方根函数比较合理、简便。
(4)平面拟合法、多项式拟合法及基于多项式的拟合推估法都能满足精度要求。不过,这与数据的质量和点位分布的均匀程度有着很大关系。
参考文献:
[1]梁正英,董鸿闻.精密水准测量的理论和实践[M].北京:测绘出版社,2004.
[2]钟连琨,黄发秀.GPS水准拟合方式的统计分析以及拟合方式的选择[J].工程勘察,2000(5).
[3]沙月进.最小二乘配置法在GPS高程拟合中的应用[J].测绘信息与工程,2000(3).
[4]姚道荣,钟波,汪海洪,等.最小二乘配置与普通Kriging法的比较[J].大地测量与地球动力学,2008,28(3).
[5]刘念.拟合推估的质量理论[D].郑州:解放军信息工程大学,2003.
[6]刘念.最小二乘插值与拟合推估[J].测绘科学,2002,27(3).
[7]Koch K R,Yang Y.Robust Kalman filter for rank deficient observation models[J].Journal of Geodesy,1998,72(8).
收稿日期:2015-10-20
中图分类号:U412.3
文献标志码:A
文章编号:1671-2668(2016)02-0088-04
