考虑公交车流运行速度的城市短时交通流预测方法研究

2016-04-20潘红范宏建

公路与汽运 2016年2期

关键词：智能交通城市交通

潘红,范宏建

(1.上海市长宁区交通管理中心,上海 200050;2.上海力阳道路加固科技股份有限公司,上海 201599)

考虑公交车流运行速度的城市短时交通流预测方法研究

潘红1,范宏建2

(1.上海市长宁区交通管理中心,上海 200050;2.上海力阳道路加固科技股份有限公司,上海 201599)

摘要:目前,短时交通流预测已成为城市智能交通发展中的一个瓶颈。文中通过对具有固定时域与周期性运行的公交车流速度的数据分析,发现公交车流运行速度与本时域内的短时交通流具有较好的相关性,对本时域内的短时交通流的运行特征会产生特定的标记作用,进而运用BP人工神经网络方法,利用公交车流运行速度来预测城市短时交通流,并将预测结果与常规城市短时交通流BP人工神经网络预测结果进行对比,验证了该方法良好的预测效果。

关键词:城市交通;智能交通(ITS);短时交通流预测;公交车流;BP人工神经网络

随着中国快速城市化,与日俱增的机动车给城市交通带来巨大压力,交通问题日益突显。智能交通ITS是有效解决城市交通问题的关键途径,其实施的一个重要环节是短时交通流的科学预测。由于短时交通流变化过程的随机性、不确定性,随着统计时间的变短,交通流变化的不确定性越来越显著。同时,城市短时交通流变化的不确定性还与上下游的交通流、天气变化、交通事故和交通环境等因素相关联。如何在具有不确定性的交通流变化过程中对城市短时交通流进行科学、准确、系统的数据分析,找出其中的规律,建立相应的预测方法和模型是需要解决的问题。在不考虑私有汽车、出租车及行人参与的混合交通流条件下,城市路网中通行的公交车流作为整个交通流的一部分,由于公交车的运行路线固定,发车规律,公交车流在道路上的运行状态变化相对具有周期性与规律性。因此,该文运用BP人工神经网络方法,对考虑公交车流运行速度的城市短时交通流预测方法进行研究。

1 原理分析

城市短时交通流预测是城市交通控制和交通诱导的一项基础性工作。对于城市交通控制和交通诱导而言,诱导周期一般不超过5 min,控制周期一般为2～5 min,因而要求城市短时交通流预测的时间短。一般把短于15 min的城市交通流预测称为城市短时交通流预测,其预测内容一般为交通量、平均速度、平均密度(或占有率)和旅行时间等。现有城市交通流短时预测的原理如下:已知i路段及i+j路段在过去p个时刻的交通流参数值vi+j(t-k)(k=1,2,…,p),求出第i路段未来k个时段内交通流状态估计值vi(t-k),其中vi+j(t-k)称为预测因子,包括时间数据和空间数据。时间数据主要是指i路段过去若干时刻间隔交通流参数及历史平均值;空间数据是指与i路段相邻上下游路段i+j当前和过去各时刻交通流参数。

通过采集某路口一天几个主要时刻t公交车流的运行速度与对应本路口10 min后即t+10 min的交通流运行速度,画出两个对应曲线的趋势变化进行对比研究(如图1所示)。

图1 公交车流运行速度变化趋势

由图1可见:在本路口随着不同t时刻公交车流运行速度的增大,t+10 min的交通流运行速度也呈增大趋势;同时,随着不同t时刻公交车流运行速度的减小,t+10 min的交通流运行速度也减小。说明在短时间间隔内,公交车流的运行速度与10 min的交通流运行速度的变化趋势具有较好的相关性,这是因为相对于普通车流运行速度,以t时刻公交车流运行速度作为预测因子的变化趋势更具有规律性与固定性。

2 数据采集

目前国内研究多集中于有时间因子影响的单点或单步预测模型,其中单点模型只考虑预测点自身历史数据,不考虑其他路段和交叉口;单步预测模型指t时刻只预测紧邻时刻t+l的交通流参数,以此类推滚动预测,在该文中即只采集预测单路口t时刻公交车流的运行速度。为此,只考虑i路段t时刻的公交车辆运行速度vi(t)作为预测因子,预测紧邻时刻t+l的交通流参数,并通过线圈检测器、微波检测器、红外检测器、视频检测器等常用检测设备对预测路口公交车流运行速度进行采集。数据采集内容包括信息ID、车牌号、数据上报时刻、所在经度、所在纬度、标记车流流向。

3 方法建模

早中期城市短时交通流预测多以回归分析和时间序列预测为主,由于主要以线性分析为基础,其无法及时反映城市交通系统中不确定与非线性状态,因而预测精度不理想。现在一些适应能力强、计算效果好、抗干扰能力强的理论方法被应用到城市短时交通流预测中,人工神经网络模型就是其中之一,因其具有实时信息更新网络、保证预测实时性的特点,与传统方法相比较,其能更有效地解决城市短时交通流预测方面的问题。

BP人工神经网络是目前应用最广泛的一种人工神经网络,它是一种多层前馈网络,包含输入层、隐含层和输出层,同层单元之间不相连,是一种单向传播、具有从输入到输出的高度非线性映射的多层前向网络。在输入层和输出层之间可有一个或多个隐含层,由信息的正向传播和误差的反向传播两个过程组成,信号向前逐层传递,不带反馈和层内相互连接结构,上层节点输出值只会影响下层节点的输入值;通过参数调整即误差反向传播过程调整网络的连接权值,在最小均方差条件下使网络输出值最大程度地接近于期望输出值。其网络结构如图2所示。下面运用BP人工神经网络方法,考虑公交车流运行速度来预测城市短时交通流。

图2 BP人工神经网络的结构

3.1 建模原则

基于BP人工神经网络的短时交通流预测模型的建立原则如下:

(1)精确性,即预测结果满足精度要求。

(2)实时性,表现为计算的复杂性,要求能在规定的时间内求出结果,及时获取交通流信息。

(3)动态反馈性,要求在发生异常情况时,能根据实际情况动态反馈,进行调整。

(4)可移植性,即模型能通过参数调整而具有时空移植性。

3.2 神经元函数

在人工神经网络中,在生物神经中神经元和突触是神经网络的基本组成部分,神经元常被称为处理单元或节点。人工神经元的假定,是对生物神经元进行简化和概括,更便于数学化表达。图3为人工神经元结构模型。

图3 人工神经元模型图

根据不同的人工神经元输入、输出特性,可采用不同的传递函数。sigmoid函数在同一网络中既能处理小信号,也能处理大信号,该函数中区的高增益解决了小信号需要放大的要求,而两侧的低增益适宜处理大的净输入信号。鉴于此,模型网络的隐含层神经元的转移函数采用sigmoid函数中取值范围为(0,1)的非线性的单极性对数函数Iogsig(S型函

数),其表达式如下:

式中:λ为S型函数的压缩系数,这里令其为1,即

由于模型输出层为单一的交叉口交通流量值,为了在输出得到具体数值,输出神经元转移函数采用线性函数purelin。

3.3 模型结构

模型中,取输入数据的维数为1,用一个一维的向量X表示;输出数据的维数为1,用一个一维的向量Y表示,即X=vi(t),Y=vi(t+1)。网络输入层、输出层的节点数均为1。

BP人工神经网络的隐含层数量和隐含层节点数的设计,从结构上决定着网络性能的优劣,它是模型建立成败的关键。隐含层一般为1～2层,该模型采用1层隐含层。对于BP人工网络的隐含层神经元数,首先根据输入节点数2n+1的经验方法来确定,该网络模型中的输入层节点为1个,暂定隐含层神经元数为3个;再通过数据样本,基于MATLAB人工神经网络工具箱的训练试验来修正网络,训练函数采用默认函数trainlm,训练步长为10 000,精度值为0.000 01,学习率为0.01。通过逐步增加或减少隐含层神经元数来调整网络,直到满意精度。

3.4 模型测试

网络模型经过MATLAB人工神经网络工具箱训练好后,输入检验样本,根据检验误差测试网络性能。利用仿真函数对训练好的网络进行检验,函数表达式如下:

a=sim(net,p)

式中:a为网络输出;net为网络对象;p为输入向量或矩阵。

若p为向量,则是单点仿真;若p为矩阵,则是多点仿真。最终确定BP人工神经网络预测模型隐含层节点数取6,输出层为1个节点,即网络初始结构为1×6×1。

4 方法应用

依据上述数据采集方法,随机对某一路口进行不同时刻实际数据采集,预测10 min后该路口的实际交通运动参量,即输入层输入采集样本为t时刻该路口公交车流的运行速度,预测t+10 min时刻该路口交通流运行速度参量。同时,为对该预测方法进行对比评价,针对常规BP人工神经网预测方法进行数据采集,即输入层输入采集样本为t时刻该路口普通车流的运行速度,预测t+10 min时刻该路口交通流运行速度参量。以均方误差MSE作为模型预测性能的评价指标,对比结果如图4和图5所示。

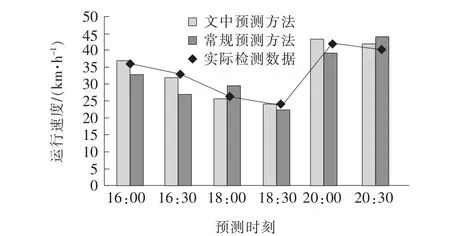
图4 交通流量预测结果对比

图5 交通流量预测均方误差MSE值对比

由图4可见:相比于常规预测方法,运用文中方法得到的不同时刻的预测值都更接近于实际值,说明文中方法较好的预测效果不具有偶然性。这是由于相对于采用本身随机性、不确定性的普通车流作为预测输入样本,采用线路固定、发车规律的公交车流作为预测输入样本具有周期性,其预测效果具有一定的可靠性。

由图5可见:文中预测方法在不同时刻的预测均方误差MSE值均在1%内,远小于常规预测方法的均方误差MSE值。说明文中方法的预测效果具有较好的稳定性。一般交通流量预测均方误差MSE值要求为1%～10%,采用文中预测方法在满足预测要求的前提下,可保证较好的精度,达到理想的预测效果。

5 结语

该文通过采集某路口一天几个主要时刻公交车流的运行速度与短时间间隔内对应该路口的交通流运行速度,发现公交车流的运行速度与下一时刻的交通流运行速度的变化趋势具有较好的相关性。运用BP人工神经网络方法,考虑公交车流运行速度来预测城市短时交通流,与常规预测方法相比,该方法在不同时刻的预测值都更接近于实际值,说明该预测方法较好的预测效果不具有偶然性,保障了预测方法应用的可靠性与稳定性,同时该预测方法在满足预测要求的前提下可保证较好的精度,达到理想的预测要求,具有较高应用价值。

参考文献:

[1]陆键,项乔君.智能运输系统(ITS)规划与应用[M].南京:江苏科学技术出版社,2008.

[2]吴浩勇.城市快速路交通参数预测方法研究[D].长春:吉林大学,2005.

[3]李贞珍.神经网络在城市交通流预测模型中的应用研究[D].上海:上海交通大学,2007.

[4]周刚.智能公交调度系统通信协议研究与实现[D].武汉:华中师范大学,2008.

[5]马寿峰,贺国光,刘豹.智能交通系统中短时交通流预测系统的研究[J].预测,2004,23(2).

[6]秦伟刚.基于人工神经网络的智能交通系统检测与控制[D].济南:山东大学,2005.

[7]戴娟莉,宋奇文.基于多因素的交通指数回归分析短时预测研究[J].公路与汽运,2015(3).

[8]范腾腾.城市道路交通流量短时预测研究[D].北京:北京交通大学,2010.

[9]刘丽娜.城市道路交通流量短时预测的研究[D].北京:北京邮电大学,2010.

[10]夏冰,董菁,张佐.周相似特性下的交通流预测模型研究[J].公路交通科技,2003,20(2).

[11]蔡岩.基于灰色预测模型的短期交通流预测研究[D].成都:西南交通大学,2009.